椭球坐标的多面函数法在区域地壳形变监测中的应用研究

胡 洋，王 璐

(西安市勘察测绘院，陕西西安710054)

一、引 言

随着各个地区区域地壳形变监测网的迅速发展，利用GPS观测资料来研究区域地壳整体运动位移变化与内部连续形变成为可能。但GPS的观测结果在WGS-84椭球定义的参考椭球面上解算地壳应变率，因此求解椭球坐标下的应变场对于区域地壳形变监测的特征分析有着非常重要的意义［1］。

二、椭球坐标下多面函数法的应变场

1.椭球面上的应变张量

根据弹性力学，应变张量矩阵是一个对称矩阵，在二维情况下由3个独立分量构成。椭球坐标下的应变张量矩阵是根据坐标转换的方法来进行，基本思想是求出坐标转换矩阵。首先在形状固定下的旋转椭球上任意一点处建立一个正交曲线坐标系，通过该坐标系坐标方向与以该椭球中心为坐标原点的固定笛卡尔坐标架的转换关系，可推算出椭球面上活动坐标系的位移梯度矩阵，从而根据该矩阵的线性组合与微分求解出旋转椭球下的应变张量［2］。因此可以将应变张量矩阵的分量写成式(1)的形式。

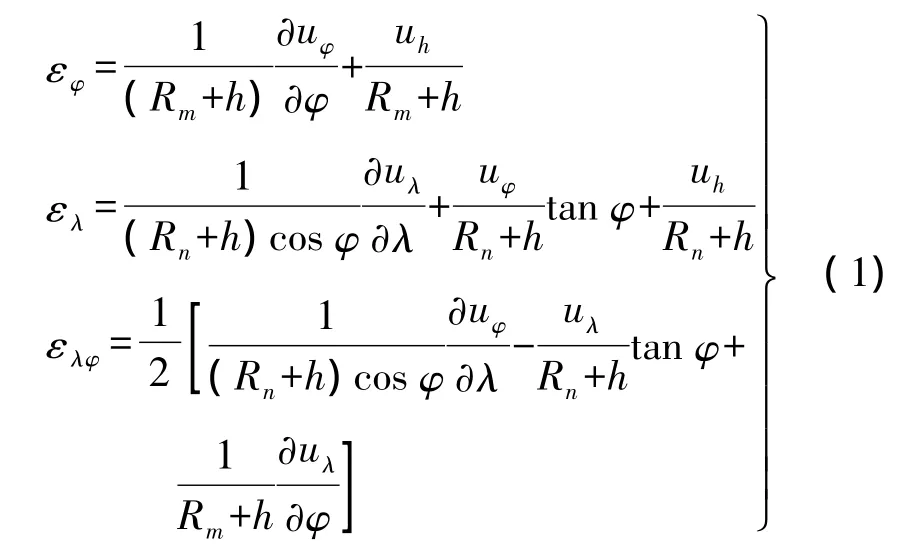
式中，h为大地高;λ为经度;φ为纬度;Rn为卯酉圈曲率半径;Rm为子午圈曲率半径［2］。当Rm=Rn=R，即椭球面变为球面时，(1)式就变为

式(2)就是应变张量在球面坐标系下解的形式。通过上述公式推导可知，应变张量的球面解形式实际上是椭球面解形式的一种特定状况［3］。由于地球的形状可以近似看成一个椭球面，因而可以忽略式(1)中的大地高及高程变化信号，令uh=0、h=0整理得

2.多面函数模型

多面函数的基本模型如式(4)所示

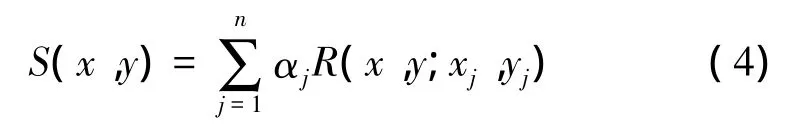
式中，n为简单数学面的张数或多层叠加面的层数，它的值与分块扩充范围内参与点的个数相等;αj为待定参数，代表了第j个核函数对多层叠加面的贡献;R(x，y;xj，yj)为核函数。为了计算方便，多层叠加面中的n个核函数一般选用同一类型的简单函数，通常是围绕竖向轴旋转的曲面，经验上在对地壳运动速率场的拟合中，选取下述函数作为核函数

式中，(x，y)为推估点的坐标;(xj，yj)为用于建立多面函数模型所选取的测点资料;δ为光滑因子;β为幂数，通过取不同的值来构建不同的核函数，β一般取值为1/2(正双曲面型)、3/2(三次曲面型)、-1/2(倒双曲面型)。在建立多面函数模型时，对于研究区域内已有的n个实测点数据。应该在其中选取m个点数据(m≤n)来建立多面函数模型

式中，S为观测值矩阵，因此有

3.椭球坐标下多面函数应变参数解算方法

对研究区域的GPS速度场的北向分量Vn与东向分量Ve，分别建立多面函数模型［3］

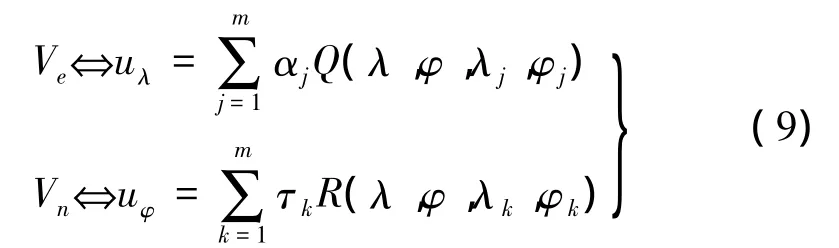
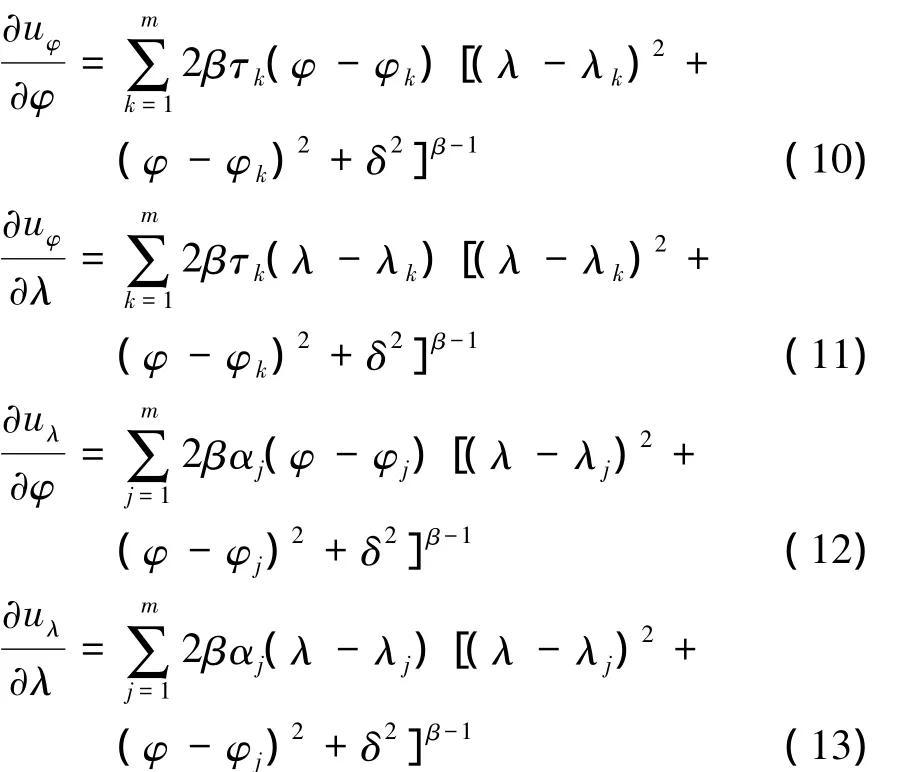
三、福建沿海地区应变率场

为了进一步研究福建地区地壳的水平形变特征分布，本文根据上述公式的推导进行了Matlab编程实现，利用一组已有的GPS拟合速度场数据，采用0.2°×0.2°的经纬格网密度，在扣除研究区域的整体刚性旋转趋势后得到其相应的剩余速度分布场，以此来研究区域地壳内部各处的相对形变特征。经过交叉验证法，建立出当 δ=1.14、β=3/2时，多面函数的建模结果最好。据此成功解算出基于多面函数法福建沿海应变场，进而由此来分析研究该区域现今地壳形变特征［4-7］。

如图1所示，福建东南沿海地区最大、最小应变率分布呈现出东南强于北西、东北强于南西的特征，其平均应变值约为4.50×10-10/a;应变率由沿海地区向内陆延伸时由大变小，并且在断裂带交接区域值达到最大。结合该地区内部相对形变场分布进行分析，发现其特征十分相近。区内主压应变优势方向较为一致，呈现出旋转方向上的NWW-SEE。主张应变轴走向近似水平，也呈现出顺时针旋转方向NE-NEE。从应变值大小来看，主张应变大于主压应变。在东南沿海地区闽江断裂、莆田—南日岛断裂以及九龙江中下游断裂与长乐—南澳断裂带的交汇地区，主张应变均显著增强，且成为该区域地壳的主应变场。结合在NW与NE向断裂的交汇处发育有福州盆地、漳州盆地及泉州盆地，且各盆地主轴线走向均为NW向，说明这一区的地形发育主要是由NW向的断裂构造带进行布控，且活动性应该以拉张为主［8］。

图中所示研究区域内地壳主应变率量级总体变化不大，只存在两个较为明显的突变区:①福建西北部地壳水平形变量明显减弱，其主应变量级约为1.00×10-10/a 至 6.40×10-11/a。该区域的微弱应变场范围大，且过渡缓慢。结合前文的论述，可以推断该区域现今地壳活动最为稳定。②东南部长乐—南澳断裂带与北西向断裂的交汇地区，地壳应变率再次出现大幅度减弱趋势，应变率约为1.94×10-10/a至6.76×10-11/a，具有空间范围小、衰减幅度大的特征;且这一衰减特征普遍适用于福建东南沿海长乐—南澳断裂带与主要的北西向断裂交汇部位，尤其是在九龙江中下游断裂的交汇部位，主压应变、张应变在空间内变化剧烈且急促，最大主压应变就分布在这一区域，其值约为4.43×10-8/a。应变率场分布显示出福建东南沿海区域地壳应力场并不均匀，且其东南变化幅度大于北东。

图2所示为福建地区地壳面膨胀值分布，其正值部分表示区域地壳处于膨胀拉张的状态，相对应的负值分布则表示该区域处于地壳的挤压缩短之中。研究区域地壳引张最为剧烈的区域位于漳州西北侧的九龙江断裂与长乐—南澳断裂带交汇区域，约为2.90×10-8/a;而在长乐—南澳断裂带的最南段，地壳压缩率达到最大值3.89×10-8/a。总体上看，福建地区压缩区域分布呈带状显示，近似北东平行于海岸线呈条带状连续分布;而在长乐—南澳断裂与北西向断裂的交汇区域依次出现相对离散化的局部引张，且地壳扩张的影响范围几乎错断了地壳缩短梯度带，进而形成了沿海岸线分布的地壳扩张—压缩交替带，在这一类地区地壳受力不均且变化较大。

图1 最大、最小主应变率

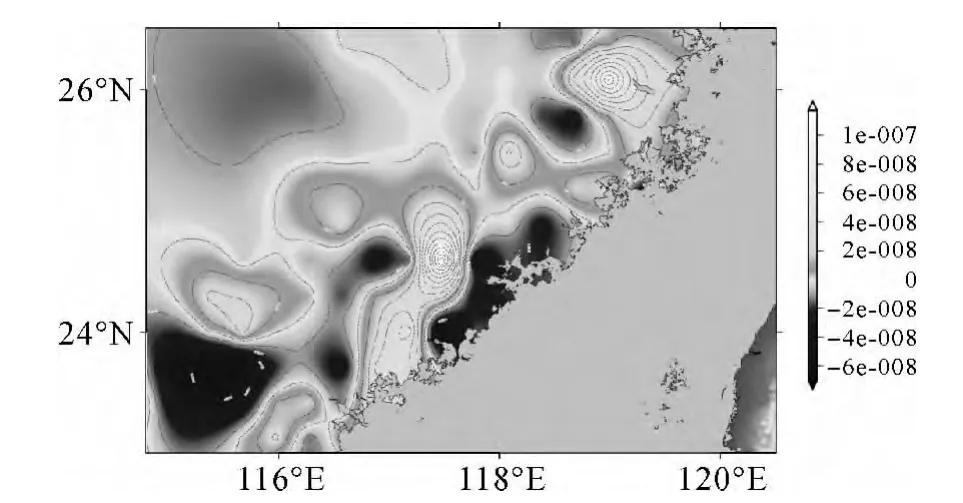
图2 面膨胀

图3为福建及其邻近地区地壳南北向地壳应变率，图中以九龙江中下游断裂带为分界，地壳南北向应变率出现显著的差异性。断裂以南，应变梯度近似东西向呈条带状展布，地壳挤压与拉张交替出现，且地壳形变趋势明显强于断裂以北。在漳州以北地区，南北向应变率梯度带近似垂直于海岸线分布。由此可以反映出研究区域地壳形变南西强于北东，且该区域地壳应力场并不均匀。东西向应变率场如图4所示，呈现出的特征与面膨胀颇为相似，说明造成区域地壳压缩或膨胀差异的主要是来自近似南北向的应力分量。结合GPS实测速度场与内部相对形变场出现的差异可以推断，福建及其邻近地区地壳形变虽然以来自印度板块北东向推挤产生的东向传递作用为主，但是其相应应力分量较为均匀。而来自菲律宾板块的北西向推挤产生的应力场则空间变化比较明显，可能是该区域地震孕震的主要构造因素。

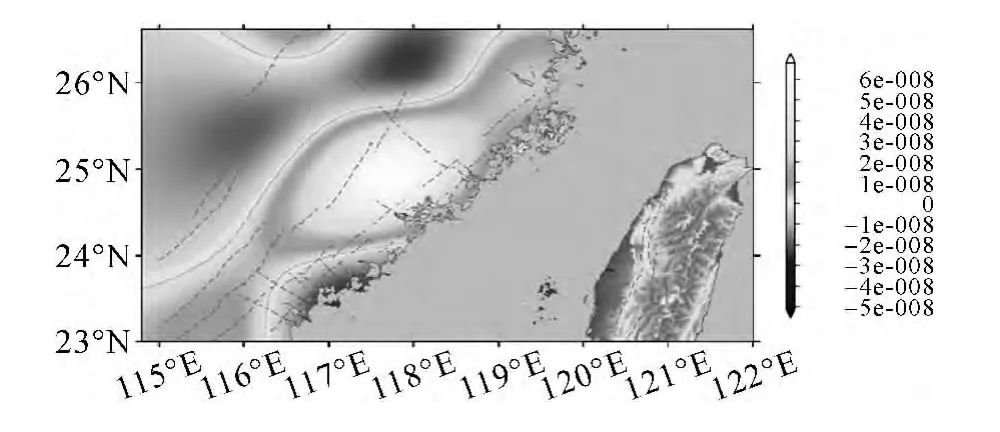
图3 南北向应变率

图4 东西向应变率

图5所示的研究区域最大剪应变普遍较小，且近似呈NE-SW的条带状分布。这与长乐—南澳断裂带现今构造活动呈现出的左旋压扭性特征发育结果和该地区最大剪应变较为一致。剪应变最大值出现在长乐—南澳断裂带与九龙江断裂带的交汇地区，其值达到 8.99×10-8/a。

图6为福建地区区域第一剪应变率场分布，图中正值区域表示该地区受到东西向伸长、南北向压缩的形变;为负值时则相反。从图中可以看出，福建地区从整个呈现由NW-SE方向的条段状展布。西北部地壳比较稳定，中部东西向伸长、南北向压缩，沿海福州、漳州城市群东西向压缩、南北向伸长，与该地区相对形变场一致。图7为福建地区第二剪应变分布图，为正值时，表示该地区收到NE-SW向伸长、NW-SE向压缩的形变;负值则相反。从图中可推断，造成福建地区的地壳压缩或膨胀差异的还受到NE-SW向的应力分量作用，在福州盆地地壳NESW向压缩、NW-SE向伸长，南部的漳州盆地则相反，因而可以判断福建地区地壳运动的受力比较复杂，差异性较高。

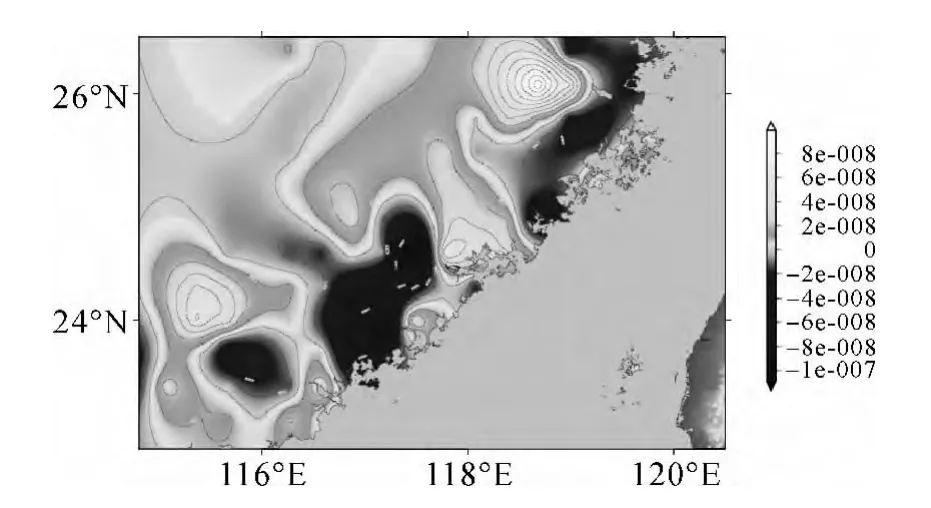
图6 第一剪应变

图7 第二剪应变

四、结 论

本文基于椭球坐标下的多面函数法建立了福建沿海地区的多面函数模型，在0.2°×0.2°格网节点GPS拟合速率场上，通过交叉验证法，认为当光滑因子δ=1.14、核函数为β=3/2时，建模效果最优。根据此多面函数模型进一步导出了基于旋转椭球面上的应变张量公式，并解算得到了福建沿海地区的各种应变场。

以往对于福建及其邻近地区沿海地壳形变特征的研究成果认为:该区域地壳形变存在东强西弱，南强北弱的总体特征。根据本文的研究结果，研究区域地壳的现今水平形变特征可能更加复杂。在总体形变的背景场相一致的基础上，局部存在较大的差异性变化。具体地，以助漳州盆地及九龙江中下游断裂为分界，可以将研究区域地壳水平形变分为两个小区。在九龙江断裂以北的沿海地区，地壳水平形变特征较为一致，基本符合南强北弱、东强西弱的特点。根据以上各个应变场的特征分析，为进一步研究区域地壳形变监测的深部驱动机制提供参考。

［1］黄声享，尹晖，蒋征.变形监测数据处理［M］.武汉:武汉大学出版社，2003.

［2］刘序俨，黄声明，林岩钊.地形旋转张量探讨［J］.大地测量与地球动力学，2010，30(5):57-63.

［3］刘序俨，黄声明，梁全强.旋转椭球面上的应变与转动张量表达［J］.地震学报，2007，29(3):240-249.

［4］吴绍祖，丁学仁，李祖宁，等.福建地区现今地壳运动变化特征研究［J］.华南地震，2005，25(3):87-94.

［5］石耀林，朱守彪.用GPS位移资料计算应变的方法的讨论［J］.大地测量学与地球动力学，2006，26(1):1-8.

［6］刘经南，施闯，姚宜斌，等.多面函数拟合法及其在建立中国地壳平面运动速度场模型中的应用研究［J］.武汉大学学报:信息科学版，2001，26(6):501-503.

［7］张贵钢，杨志强，王庆良，等.基于最小二乘配置模型探讨青藏高原巴彦喀拉块体的运动特征［J］.地球科学与环境学报，2011，33(2):213-216.

［8］CHEN Z，BCB，LIU Y，etal.Global Positioning for India/Eurasia intercontinental deformation［J］.Geophys Res，2001(105):16215-16227.