GNSS定位成果在不同ITRF框架间的转换方法研究

刘演志

(广州市城市规划勘测设计研究院，广东广州510060)

一、引 言

国际地球参考框架(international terrestrial reference frame，ITRF)是一个地心参考框架，由空间大地测量观测站的坐标和运动速度来定义，是国际地球自转服务的地面参考框架［1-9］。GNSS直接定位成果一般为ITRF框架结果，但由于章动、极移的影响及国际协定地极原点CIO变化，导致ITRF参考框架每时刻都在变化。尽管ITRF参考框架是随着时间而变化的，但无论是处于哪个框架哪个历元都可以根据一定的转换方法向任何的一个框架及对应历元转换。涉及到的转换过程有:①同一参考框架下不同历元转换;②同一历元不同参考框架转换;③不同参考框架不同历元转换。实现以上3个过程的方法有两种:①速度场法:在同一ITRF坐标参考框架下，利用速度场法实现不同历元的坐标归算;对于同一历元不同ITRF参考框架的坐标转换采用IERS公布的14转换参数进行基准转换;对于不同参考框架不同历元的转换，需要先进行源坐标参考框架下的历元转换，然后在同一历元下进行同历元不同参考框架转换。②约束平差法:获取测站点与就近IGS跟踪站的基线向量，然后选取要获取的ITRF框架及历元的IGS站的坐标(可在IERS网站获得)根据约束平差方法获得测站点所需要的ITRF框架坐标。在约束平差法中还会涉及速度场的内插计算。

二、原理与方法

1.速度场转换法

每一个ITRF参考框架都是由空间大地测量观测站的坐标和运动速度来定义，具体数据都能在IERS网站上获得。同一ITRF坐标框架下不同历元的转换公式如下

式中，Vx、Vy和Vz为观测站在该ITRF参考框架下的运动速度;t0为参考历元;t为待求历元。如果该点位IGS跟踪站点，则很容易从IERS网站上获取该点的速度，但是对于一般的测量点，该点的速度是未知的，也无法从IERS网站获得，可采用欧拉矢量方法获得，公式如下式中，Vx、Vy和Vz为观测站在该ITRF参考框架下的运动速度;X、Y、Z为该点ITRF参考框架下的坐标;Ωx、Ωy和Ωz为3个欧拉矢量。利用至少3个IGS跟踪站坐标及速度采用最小二乘平差方法即可获得3个欧拉矢量 Ωx、Ωy和Ωz，然后根据计算点的 X、Y、Z坐标即可求得计算点的速度参数，进而进行有关历元转换。

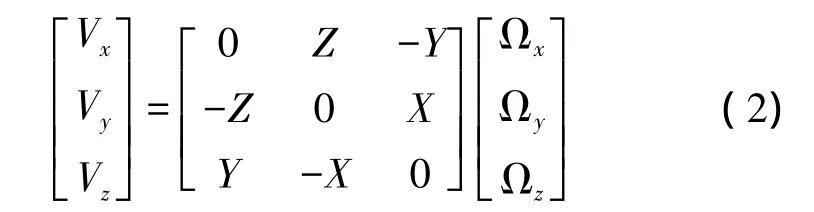
同一历元下不同ITRF框架转换方法一般采用经典七参数转换，并考虑转换参数随时间的变化率，转换模型公式如下

ITRF坐标框架间的转换首先应获取转换公式的七参数，七参数的变化率乘以转换历元与标准历元的历元差得到转换历元下七参数的变化大小，与七参数标准值相加得到转换公式所需的七参数，公式如下

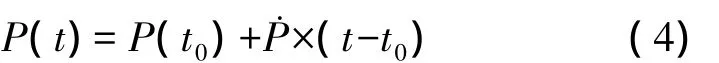
得到所需的七参数后，将点位信息与七参数代入转换公式，则可达到同一历元下ITRF坐标框架间的转换。式(3)和(4)转换所需要的转换参数可在IERS网站获得。

2.约束平差方法

约束平差方法的原理是利用计算点的坐标与就近的IGS跟踪站坐标(同一历元时刻，首先将IGS跟踪站坐标历元转换为相同历元)获得点间的基线向量，然后将IGS跟踪站坐标作为约束点，通过约束平差方法获得计算点的坐标。基于基线向量平差的误差方程式可写为［10］

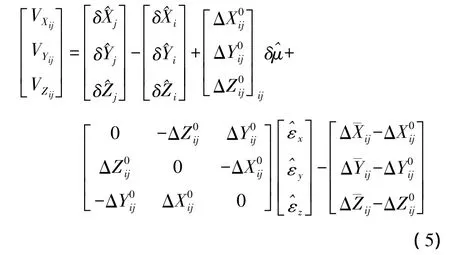
式中， [δX^iδY^iδZ^i]、[ δX^jδY^jδZ^j]为国家坐标系下(i，j)点的三维坐标改正数;(ΔX珔，Δ珔Y，ΔZ珔)为WGS-84坐标下的基线观测值、和为旋转参数;δμ^为尺度参数;上标“0”表示变量的近似值。

但该方程秩亏，需附加约束条件才可以进行约束平差，若K点的大地纬度、大地经度和大地高已知，则可列立约束条件:

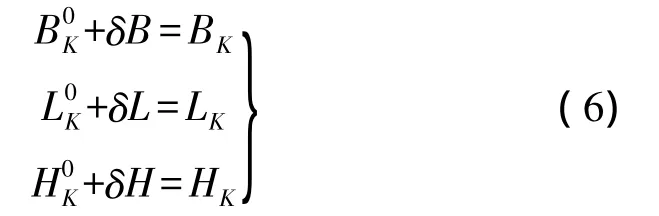
三、结果分析

笔者采用模拟计算方法对本文两种方法进行精度分析，选取 4个 IGS跟踪站 BJFS、SHAO、WUHN和KUNM，并将WUHN站作为待求点展开研究。所有计算结果都与IERS公布结果进行比较，速度场法计算得到的WUHN站的速度见表1，结果与IERS公布结果差异较小;坐标转换结果见表2，转换结果的平面和高程精度均约5 cm;采用约束平差方法结果见表3。结果显示，转换结果的平面和高程精度均可以达到5 cm。

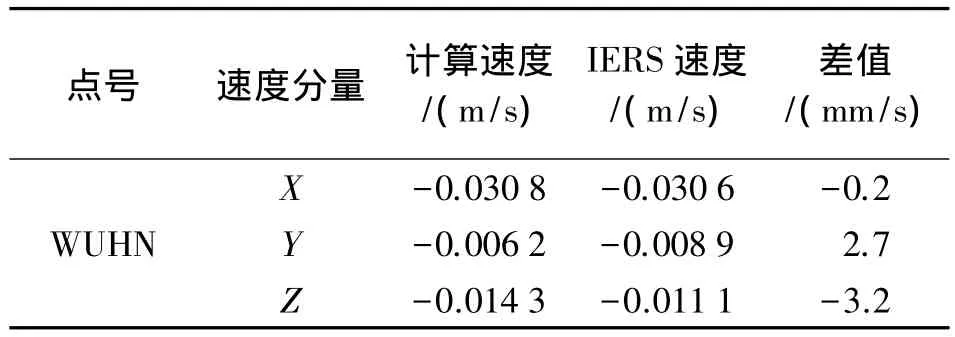
表1 WUHN站ITRF1997框架1997.0历元速度

表2 速度场转换方法结果与IERS公布结果的比较

表3 约束平差方法获得的结果与IERS公布结果的比较

四、结束语

本文对ITRF框架及历元转换的两种常用方法(速度场法和约束平差法)展开研究，并利用4个IGS跟踪站的数据对两种方法的精度进行分析，结果表明，两种转换方法均可获得5 cm左右的转换精度。在实际工程中，精密单点定位技术越来越广泛地被应用在实际生产中，但精密单点定位结果的基准一般是ITRF参考框架，而我国采用的CGCS2000坐标是ITRF97框架2000.0历元，采用本文方法可方便地将精密点定位结果转换为CGCS2000坐标。

［1］党亚民，成英燕，薛树强.大地坐标系统及其应用［M］.北京:测绘出版社，2010.

［2］陈俊勇.大地坐标框架理论和实践的进展［J］.大地测量与地球动力学，2007(4):1-6.

［3］杨元喜.2000 中国大地坐标系［J］，科学通报，2009，54(16):2271-2276.

［4］朱文耀，熊福文，宋淑丽.ITRF2005简介和评析［J］.天文学进展，2008，26(1):1-14.

［5］陈仲怀，廖超明，宋传峰，等.基于 PPP的 CGCS2000坐标计算方法研究［J］.测绘通报，2014(2):10-12.

［6］杨建华，杨志强，王腾军，等.一种ITRF框架坐标的间接测量方法［J］.测绘通报，2005(10):25-27.

［7］符养，韩英.ITRF2000和新的全球板块运动模型［J］.测绘学院学报，2002，19(2):85-87.

［8］刘立，成英燕.ITRF框架的相互转化［J］.大地测量与地球动力学，2010，30(2):141-143.

［9］党亚民，秘金钟，成英燕.全球导航卫星系统原理与应用［M］.北京:测绘出版社，2007.

［10］施一民.现代大地控制测量［M］.北京:测绘出版社，2003.