常用稳健估计方法应用于概率积分法参数求取时的有效性研究

王晓辉，姜佃高

(太原理工大学测绘科学与技术系，山西太原030024)

一、引 言

开采沉陷预计可以定量地研究开采影响的地表移动变形在时间和空间上的分布规律，对“三下”开采也具有重要指导作用。而开采沉陷预计方法中应用最为广泛的是概率积分法，其预计结果的精度主要取决于预计参数的可靠性［1］。因此，准确确定概率积分法参数对开采沉陷理论和生产实践都具有重要意义。

概率积分法的预测参数一般根据地表移动观测站实测资料通过最小二乘曲线拟合确定，最小二乘法有极好的配赋误差的能力，但它易受粗差的影响，使参数估值失真［2-4］。当观测值中不可避免地存在粗差时［5-6］，稳健估计求参技术具有有效抵御粗差或异值对参数干扰的特性，能够克服最小二乘法拟合求参时常出现的结果发散问题，保证求参结果的可靠性［7-8］。然而，不同稳健估计方法的稳健特性不同。Mitra等［9］研究表明，考虑到重尾噪声分布，Huber法和Andrews法的稳健性要优于L1法。Li等［10］指出Fair法的稳健性要优于 L1法。Pennacchi［11］通过算例表明，在迭代 100次的情况下，Cauchy法比German-McClure法、Welsch法和Tukey法效果更好。方俊涛等［12］研究认为，Welsch法的稳健性最好，其次是Tukey法，Huber法的稳健性最差。李惠芬等［13］分析指出，Andrews法、Tukey法和IGG方案均优于Fair法。

本文在嘉乐泉煤矿实测资料基础上进行人工异值干扰求参试验，以观测值中含有不同粗差值为例，比较了13种常用稳健估计方法求取概率积分法参数时的稳健特性。

二、概率积分法参数的稳健估计

1.概率积分法参数的稳健估计模型

概率积分法参数的稳健估计模型详细见文献［14］。

2.改进算法麦夸尔特法

用曲线拟合求取实测参数的基本算法是泰勒级数展开法，但其存在一个缺点，即当各参数初始值选的偏离其真值过大时，各次求得的各参数值可能不逐渐趋近于真值(称为迭代收敛)，而是越来越偏离真值(称为迭代发散)。为了克服这个缺点，放宽对初始值的限制，采用其改进算法，即麦夸尔特法。

首先选取参数 bi(i=1，2，…，m)的初始值可从经验值中选取，也可根据本矿区已有的实参数据求出，则有(Δi为第i个参数的修正值)

将f(Xk;B)附近按泰勒级数展开，并假设与bi足够接近，使Δi足够小，并可在展开式中略去Δi的二次及二次以上的项，则有

式中

根据最小二乘原理VΤV=min，则有

即

写出m个未知数Δi的线性方程组，并进行整理、移项，则上式可写作

式中

上述中的d称为阻尼因子，是一个≥0的可调整的常数，其作用是适当选择d可使每次迭代后求得的Q'值均较迭代前的值小。d值的选择原则是:在迭代收敛时，d选取较小的值，以减少迭代次数;在迭代后的Q'值大于迭代前的值时，将d值放大，重新进行迭代，直至迭代后的Q'值比迭代前的值小为止，这样能保证经过一次迭代Q'就减少一次，bi的值就向其真值接近一步，从而大大放宽了对接近bi的要求，最终可求得各参数值bi。对应于概率积分求参下的参数有下沉系数q，主要影响角的正切 tanβ，主要影响传播角 θ0和点偏移距 s1、s2、s3、s4等参数。

三、常用稳健估计方法和稳健性比较

1.常用稳健估计方法

13种常用的稳健估计方法及它们的调和系数见文献［15］。

2.两种参数估计方法的比较

为了比较任意两种参数估计方法在人工异值干扰试验下哪种方法更有效，给出参数的相对减益的概念，简述如下:

定义:在概率积分求参中，当观测值中不存在粗差时，通过最小二乘曲线拟合法求得的参数理论上是最优值，而当观测值中存在粗差时通过各种稳健估计方法求得同一参数的值与无粗差的最小二乘曲线拟合法求得的参数值会发生变化，二者之间的差值与无粗差的最小二乘曲线拟合法求得的参数比值的绝对值的百分数就称作参数的相对减益。当用稳健估计方法求得参数的相对减益越大，说明这种方法越不稳健;反之，其值越小则越稳健。

在概率积分求参中选取3个主要参数:下沉系数q、主要影响角的正切tanβ和拐点偏移距D=(H0为平均采深)。令下沉系数q的相对减益为

主要影响角的正切tanβ的相对减益为

拐点偏移距D的相对减益为

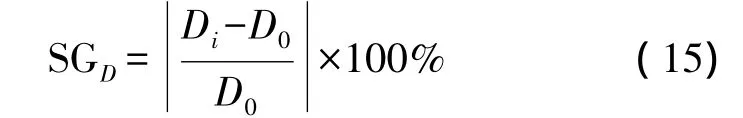
上式中，当观测值中不存在粗差时，通过最小二乘曲线拟合法求得的3个主要参数值为下沉系数q0、主要影响角的正切tanβ0和拐点偏移距D0;当观测值中存在粗差时，通过各种稳健估计方法求得的3个主要参数值为下沉系数qi、主要影响角的正切tan βi和拐点偏移距 Di(i=1，2，3，…，13)，i为所选的第i种稳健估计方法。

四、结果与讨论

基于嘉乐泉煤矿某工作面地表移动走向观测线实测资料，通过人为地增加一些异值点的办法，进行人工干扰稳健求参试验。该工作面采用走向长壁采煤法采煤，全部陷落法管理顶板，上覆岩层岩性综合评价为中硬，地表沉陷规律基本符合概率积分模型，地表线A是半无限开采，其实测下沉值见表1。本文采用将走向观测线的拐点和最大下沉点处第一次加上100 mm粗差，第二次加上200 mm的粗差，经计算得出了13种常用稳健估计方法与无粗差下最小二乘法3个主要参数的相对减益，其结果如图1—图3所示。

表1 走向观测线地表下沉值

图1 不同稳健估计方法相对于无粗差的最小二乘法下沉系数的相对减益

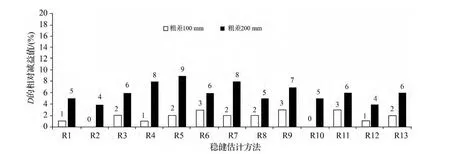
图2 不同稳健估计方法相对于无粗差的最小二乘法拐点偏移距的相对减益

图3 不同稳健估计方法相对于无粗差的最小二乘法的主要影响角正切的相对减益

由图1可看出，当粗差取100 mm时，L1法和German-McClure法下沉系数的相对减益均为0%，其次是IGGIII方案，其相对减益为1%，其余方法的结果都≥2%;当粗差取200 mm时，L1法和IGGIII方案相对减益均为6%，而German-McClure法下沉系数的相对减益为7%，其余方法的结果都≥8%。

由图2可看出，当粗差取100 mm时，L1法和German-McClure法拐点偏移距的相对减益均为0%，而IGGIII方案的相对减益为1%，其余方法的结果都≥2%;当粗差取200 mm时，L1法和IGGIII方案相对减益均为4%，而German-McClure法拐点偏移距的相对减益为5%，其余方法的结果都≥6%。总体上看各个稳健估计方法的拐点偏距的相对减益相差不是很大，都在9%以内。

由图3可看出，当粗差取100 mm时，L1法、L1-L2法和German-McClure法主要影响角正切的相对减益均为 0%，而是 Huber法、Andrews法、Welsch法、Tukey法、Danish法、IGG 方案、IGGIII方案和Cauchy法主要影响正切的相对减益为1%，各方法的结果都特别接近，都不大于3%;当粗差取200 mm时，L1法、German-McClure法和IGGIII方案相对减益均为4%，其余方法的结果都≥6%。

五、结束语

综合图1、图2和图3的试验结果，可知当给走向观测线的拐点和最大下沉点处同时加上100 mm的粗差时，对于各稳健估计方法3个主要参数的相对减益相差都不是很大，其中 L1法、German-McClure法和IGGIII方案相对更稳健;当给走向观测线的拐点和最大下沉点处同时加上200 mm的粗差时，各稳健估计主要参数相对减益值差异逐渐增大，而 L1法、German-McClure法和IGGIII方案的3个主要参数相对减益值比其他稳健估计方法的都小。对于概率积分法参数的稳健估计方法，L1、German-McClure方法和IGGIII方案较其他稳健估计方法相对更稳健。

［1］何国清，杨伦，凌赓娣，等.矿山开采沉陷学［M］.徐州:中国矿业大学出版社，1994.

［2］王素立，刘永.基于波动相关性及主分量变换的多元线性回归模型研究［J］.统计与决策，2012(22):18-21.

［3］高山，李孝军.关于最小二乘法的稳健性分析［J］.统计与决策，2006(8):125-126.

［4］何霞，刘卫锋.基于全最小一乘准则的灰色GM(1，1)模型参数估计［J］.统计与决策，2006(8):30-33.

［5］GRIEP M I，WAKELING I N，VANKEERBERGHEN P，et al.Comparison of Semi-robust and Robust Partial Least Squares Procedures［J］.Chemometrics and Intelligent Laboratory Systems，1995，29(1):37-50.

［6］GUO JF，OU J K，WANG H T.Robust Estimation for Correlated Observations:Two Local Sensitivity-based Down Weighting Strategies ［J］.Journal of Geodesy，2010，84(4):243-250.

［7］吴健平，张立.地理数据线性回归中的稳健估计方法［J］.干旱区地理，1994，17(1):83-88.

［8］冯守平，石泽，邹瑾.一元线性回归模型中参数估计的几种方法比较［J］.统计与决策，2008(24):152-153.

［9］MITRA S，MITRA A，KUNDU D.Genetic Algorithm and M-Estimator Based Robust Sequential Estimation of Parameters of Nonlinear Sinusoidal Signals［J］.Communications in Nonlinear Science and Numerical Simulation，2010，16(7):2796-2809.

［10］LI H F，JIANG X Q，LI Z.Robust Estimation in Gaussian Filtering for Engineering Surface Characterization［J］.Precision Engineering，2004，28(2):186-193.

［11］PENNACCHI P.Robust Estimate of Excitations in Mechanical Systems Using M-Estimators-Theoretical Background and Numerical Applications［J］.Journal of Sound and Vibration，2008，310(4-5):923-946.

［12］方俊涛，何桢，宋琳曦.响应曲面建模的稳健M-回归方法［J］.工业工程，2012，15(3):98-103.

［13］李惠芬，蒋向前，李柱.高斯滤波稳健性能的研究与改进［J］.仪器仪表学报，2004，25(5):633-637.

［14］郭广云，汪云甲.概率积分法参数的稳健估计模型及其应用研究［J］.测绘学报，2000，29(2):162-165.

［15］GE Y H，YUAN Y，JIA N N.More Efficient Methods among Commonly Used Robust Estimation Methods for GPS Coordinate Transformation ［J］.Survey Review，2013，45(330):229-234.