一种改进的LLR-SPA译码新算法*

王 岩，王中训，唐田田，刘为云，高兴龙

(烟台大学 光电信息科学技术学院，山东 烟台 264005)

0 引言

低密度奇偶校验码(Low Density Parity-Check，LDPC)是一种误码性能逼近香农极限的实用码，并且能够做到完全的并行译码，一直以来备受研究者的关注。近年来随着其编码和译码算法的不断改进与完善，该码在深空、水下、移动通信等领域得到了较为广泛的应用[1-4]。

LDPC码的译码算法是建立在无环Tanner图上的置信传播(Belief Propagation，BP)算法。基于概率域的BP译码算法涉及大量的加法和乘法运算，其又被称作和积(Sum-Product Algorithm，SPA)算法。该算法中的乘法运算不仅会消耗大量运算时间，而且不利于量化实现[5-6]。针对此问题，研究者提出使用似然比表示概率消息，用加法运算代替大量乘法运算，基于此方法提出的译码算法被称为 LLR-SPA（Sum-Product Algorithm in Log-Likelihood-domain)算法，LLR-SPA算法的提出为 LDPC码的实际应用打下了坚实的基础。

LLR-SPA算法虽然极大地降低了BP算法的复杂度，但是其译码复杂度仍然较高，限制了LDPC码的进一步应用。目前，专家学者为LDPC码的实际应用做了诸多贡献。参考文献[7]提出了一种基于LLR-SPA算法的改进的MS(min-sum)译码算法，该算法虽然降低了LLR-SPA译码算法的复杂度，但其译码性能相对较差，难以满足对译码性能要求较高的应用。参考文献[8-9]提出了一种基于LLR-SPA算法的改进的OMS(offset min-sum)译码算法和 NMS(normalized min-sum)译码算法，这两种算法虽然能够提供较高的译码精度，但是要根据实际情况设置相关的偏移参数和校正因子，增加了译码复杂度，而且也不利于硬件实现。参考文献[10-11]分别提出了一种基于一阶迈克劳林级数和一阶泰勒级数简化的译码算法，这两种算法虽然能有效地降低译码复杂度，但是牺牲了译码精度。基于此，本文提出一种基于泰勒级数分段线性近似的简化算法，该算法是将LLR-SPA译码算法中复杂度较高的雅克比修正项采用泰勒级数进行分段线性近似，在译码复杂度相当的情况下，大大提高了译码精度。

1 LDPC码的译码算法

1.1 LLR-SPA译码算法

LDPC 码根据检验矩阵 Hm×n传送的码字 x={x1，x2，…，xn}和接收的码字 y={y1，y2，…，yn}进行译码。

信息经过编码，采用BPSK调制，通过AWGN信道传输，其信道的噪声方差为σ2，每个变量节点的先验似然比是 L(xn)=log{P(xn=0|yn)/P(xn=1|yn)}，则 LLR-SPA算法的译码过程如下：

(1)初始化，变量节点传向校验节点的初始信息和校验节点传向变量节点的初始信息，其计算公式分别如式(1)、式(2)所示：

(2)校验节点的更新，对于每一行 m，n∈N(m)，N(m)表示与校验节点m相连的所有变量节点的集合，n′=N(m) ，N(m) 表示N(m)中去掉变量节点n。计算公式为：

(3)变量节点的更新，对于每一列 n，m∈M(n)，M(n)表示与变量节点n相连的所有校验节点的集合，m′=M(n)m，M(n)m表示M(n)中去掉校验节点m。计算公式为：

1.2 基于泰勒级数的简化译码算法

本文提出的算法是针对LLR-SPA算法中复杂度较高的雅克比修正项采用泰勒级数进行分段线性近似，主要是对其校验节点进行更新，对于式(3)中的tanh运算采用参考文献[12]中的核心操作对式(3)重新处理得到式(7)。其中式(7)中的两个非线性的对数函数是雅可比修正项。

从校验节点获得外部信息：

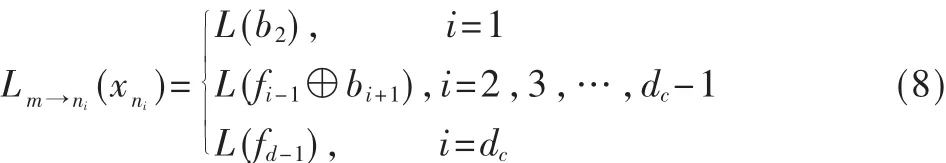
其中，U、V表示统计独立的二进制随机变量，L(U)、L(V)是 U、V的似然比值，fi、bi分别表示一组辅助的二进制随机变量，i=1，2，…，dc，dc表示 LDPC 码的校验度，⊕表示模二操作。

利用式(7)和传送的码 字 x={x1，x2，…，xn}对辅助的二进制随机变量 fi、bi分别作递归处理，得到 L(fi)和 L(bi)。利用公式(xn1⊕xn2⊕…⊕xnd)=0，得到 xni=(fi-1⊕bi+1)，其c中i∈{2，3，…，dc-1}。通过这种前向后向递归运算完成校验节点的更新。

[11]使用一阶泰勒级数对式(7)中的修正项进行处理。本文提出的算法与该算法与原曲线的最大误差对比结果如表1所示，本文提出的算法与参考文献[11]提出的算法近似曲线的对比结果如图1所示。本文采用泰勒级数对式(7)中的修正项进行分段线性近似。使用函数g(x)=log(1+e-|x|)表示式(7)中的修正项，在一阶泰勒级数近似的基础上对曲线g(x)进行分段线性近似，并以g(x)函数切点x0为分段节点进行分段，分段步长为0.75，分段函数如表2所示。

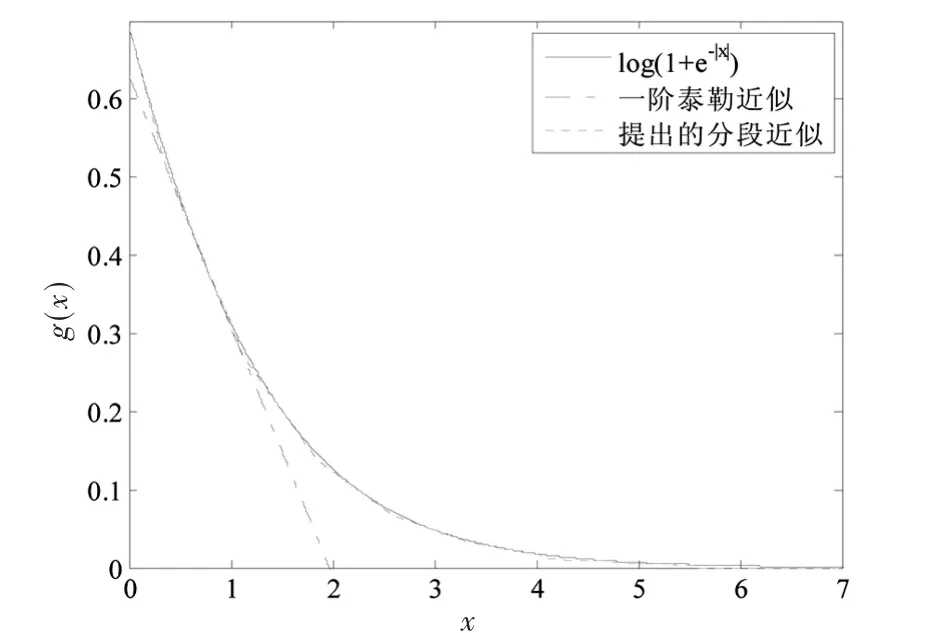
图1 两种线性近似曲线

表1 两种线性近似方式与原曲线的最大误差

从图1可以看出本文提出的算法有效地解决了参考文献[11]提出的使用一阶泰勒级数近似时在x=0和g(x)=0处造成误差的问题。

该算法与LLR-SPA算法相比，在译码性能基本没有变化的情况下，避免了查表操作和非线性的对数运算，降低了算法的复杂度。与两种修正的MS译码算法相比无需设置偏移参数和校正因子，更利于实际应用。

2 仿真结果

实验使用MATLAB从以下几个方面进行验证：与原曲线的最大误差；信噪比和误比特率。实验环境如下：信道采用AWGN信道，调制方式为BPSK，规则的LDPC码(504，3，6)和(6 000，3，6)，迭代次数分别设为 40 和 80。

从表1数据可以看出，本文提出的算法相比于文献[11]提出的算法与原曲线的最大误差小，更接近原曲线。

在迭代次数为 40，使用规则 LDPC码(504，3，6)的情况下，本文提出的算法与LLR-SPA算法、最小和译码算法、一阶泰勒级数近似算法在信噪比和误比特率方面对比结果如图2所示。

图 2 规则 LDPC码（504，3，6）的译码性能，迭代次数为 40

从图2可以看出，当误码比特率为10-4时，本文提出的算法在译码性能上优于一阶泰勒级数算法和最小和算法分别约为0.15 dB，0.35 dB。相比于最优的LLRSPA算法，仅有0.05 dB的性能损失。

在迭代次数为 80，使用规则 LDPC码(6 000，3，6)的情况下，本文提出的算法与LLR-SPA算法、最小和译码算法、一阶泰勒级数近似算法在信噪比和误比特率方面对比结果如图3所示。

图 3 规则 LDPC码（6 000，3，6）的译码性能，迭代次数为 80

从图3可以看出，当误码比特率为10-4时，本文提出的算法分别优于一阶泰勒级数算法和最小和算法分别约为 0.2 dB，0.55 dB；当误码比特率为 10-5时，本文提出的算法分别优于一阶泰勒级数算法和最小和算法分别约为0.22 dB，0.6 dB。从图中还可以看出本文提出的算法与最优的LLR-SPA算法相比，几乎没有性能损失。

3 结论

本文旨在提出一种提高译码精度的新算法，该算法将LLR-SPA译码算法中复杂度较高的雅克比修正项采用泰勒级数进行分段线性近似。该算法与一阶泰勒级数近似相比在译码复杂度基本不变的情况下，极大地提高了译码算法的性能；与LLR-SPA译码算法相比，不仅避免了查表操作和复杂的非线性对数函数的计算，而且在性能上逼近最优的LLR-SPA译码算法，具有有效性和实用性。

参考文献

[1]沈雪梅.下一代无线局域网中LDPC译码算法研究[J].科技通报，2013，29(2)：127-129.

[2]Wang Kaiyao，Xiao Yang，KIM K.Construction of timefrequency codes based on protograph LDPC codes in OFDM communication systems[J].Journal of Systems Engineering and Electronics，2012，3(23)：335-341.

[3]乔晓峰，刘跃敏，宁永海.RS码与QC-LDPC码的级联码在浅海信道中的性能研究[J].电子技术应用，2012，38（5）：122-124.

[4]李成福，卢选民，杨杰，等.基于LDPC码和物理层网络编码的联合信道编码技术[J].微型机与应用，2013，32(17)：41-43.

[5]吴斌，杨波，叶明.LDPC硬件实现中的数据量化位数选择及其性能仿真[J].信息通信，2012，118(2)：26-28.

[6]梁伟，刘亮，沈旭，等.采用动态量化的低存储空间 LDPC译码研究[J].计算机工程与应用，2011，47(10)：106-109.

[7]吴琼，梅进杰.改进Min-sum的 LDPC译码研究[J].无线电通信技术，2012，38(2)：27-29.

[8]陈旭灿，刘冬培.改进的 LPDC译码算法研究[J].电子科技大学学报，2010，39(2)：219-222.

[9]Hu Xiaoyu，ELEFTHERIOU E，ARNOLD D M，et al.Efficient implementations of the sum-product algorithm for decoding LDPC codes[C].Global Telecommunications Conference，IEEE GLOBECOM(2)，2001：1036-1036E.

[10]PAPAHARALABOS P，MATHIOPOULOS P T.Simplified sum-product algorithm for decoding LDPC codes with optimal performance[J].Electronics Letters，2009，45(2)：116-117.

[11]胡树楷，王新梅.一种简化的GF(q)-LDPC码译码算法[J].西安电子科技大学学报，2011，38(2)：8-12.

[12]Chen Jinghu，DHOLAKIA A，ELEFTHERIOU E，et al.Reduced-complexity decoding of LDPC codes[J].IEEE Transactions on Communications，2005，53(8)：1288-1299.