导管架管节点穿透裂纹应力强度因子数值分析

薄景富,杨树耕,李 铎,周 楠

(1.天津大学a.水利工程仿真与安全国家重点实验室;b.建筑工程学院,天津300072;2.海洋石油工程股份有限公司,天津300461)

导管架管节点穿透裂纹应力强度因子数值分析

薄景富1a,b,杨树耕1a,b,李 铎2,周 楠2

(1.天津大学a.水利工程仿真与安全国家重点实验室;b.建筑工程学院,天津300072;2.海洋石油工程股份有限公司,天津300461)

采用有限元软件ANSYS建立多个不同尺寸的撑杆焊趾处带穿透裂纹的导管架平台T型管节点有限元模型,载荷分别为施加在撑杆上的轴力和平面内弯矩,采用位移外推法计算裂纹前缘的应力强度因子。首先验证ANSYS计算的管节点撑杆焊趾处穿透裂纹应力强度因子结果随裂纹前缘网格尺寸变化的收敛性,然后初步讨论管节点撑杆壁厚和穿透裂纹角度半宽值对撑杆焊趾处穿透裂纹应力强度因子的影响,得出了应力强度因子随撑杆壁厚和穿透裂纹角度半宽值的变化规律,可为工程中管节点的止裂工作提供参考。

导管架平台;管节点;撑杆;穿透裂纹;应力强度因子;有限元法

导管架平台在我国浅海油田中应用广泛,长期承受风、浪等疲劳载荷作用,而管节点处存在显著的应力集中,因此导管架管节点疲劳寿命问题不可避免。目前裂纹结构的疲劳寿命的断裂力学评估方法皆基于1963年Paris和Erdogan提出的Paris方程为核心的疲劳断裂理论[1,2]。Paris方程通过裂纹前缘的应力强度因子得出裂纹疲劳扩展速率,继而求得裂纹疲劳寿命,因而疲劳裂纹前缘的应力强度因子SIF的计算尤为重要。

应力强度因子的计算起步于对平板问题的解析解,对于一些含特殊结构的裂纹应力强度因子的解,已经整理成几本可以供工程人员查阅的手册[3-5]。近年来国内外学者对管节点弦杆焊趾处的表面裂纹的应力强度因子做了许多试验测试和数值分析工作,取得了值得关注的成果[6-16]。Lie[17-18]仅研究了T、Y型管节点弦杆焊趾处表面裂纹和穿透裂纹的有限元网格划分方法,并没有对结果做出分析。总体来说,在管节点穿透裂纹方面的研究,目前尚未有足够的工作。

在导管架上常见的薄壁管节点中,弦杆是重要的立柱结构,而撑杆则是次要的横撑或斜撑结构,撑杆不仅直径较弦杆小,而且壁厚也远小于弦杆,因而撑杆在焊趾处更容易出现穿透裂纹。出于安全性的保守设计理论,认为带穿透裂纹的管节点结构已经失效,但实际上作为次要结构的一个甚至一组撑杆出现穿透裂纹,管节点依然有承载能力,因而基于断裂力学的管节点撑杆焊趾处穿透裂纹的研究对于提高导管架的经济性方面是必要的。

1 位移外推法计算应力强度因子

应力强度因子的理论计算方法有多种,主要分为直接法和间接法两类,直接法有应力外推法和位移外推法,间接法有J积分法和能量释放率法,由于在弹性材料范围内,位移外推法在计算代价、成熟程度、精度等方面都能令人满意,故在此采用位移外推法计算应力强度因子。

运用位移外推法就是应力强度因子最重要的就是要得到裂纹前缘的位移场,G.R.Irwin利用Westergard半逆解法提出了适用于裂纹前缘附近位移场近似解的表达式。如图1建立裂纹前缘的局部坐标系,在平面应变假设下三类裂纹的位移场表达式为[19]:

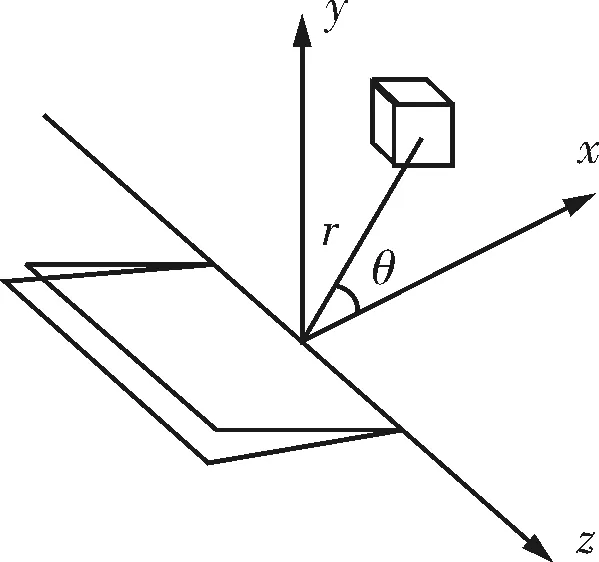
图1 裂纹前缘坐标系

Ⅰ型裂纹:

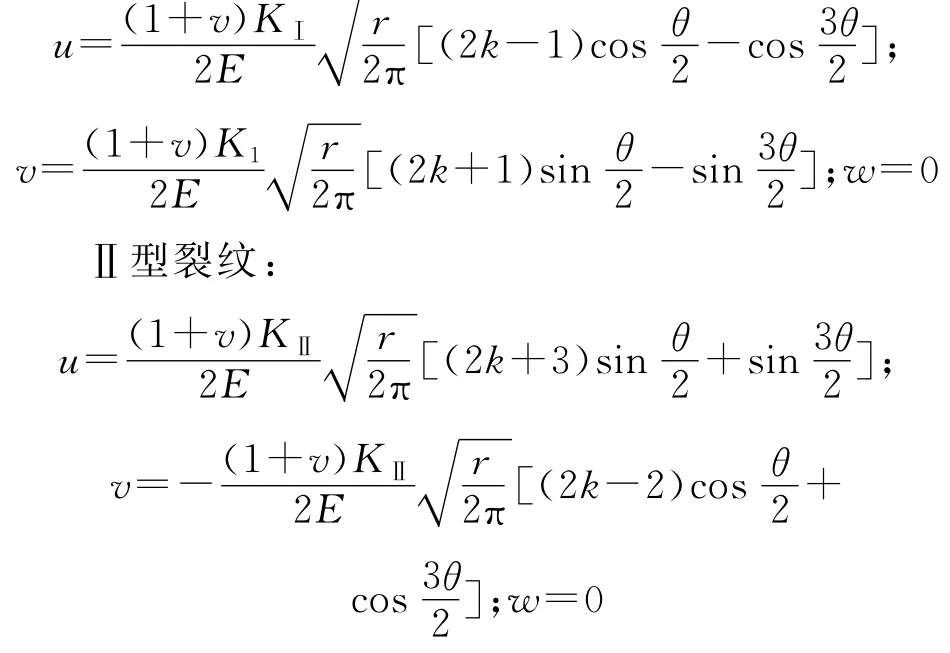
Ⅲ型裂纹:

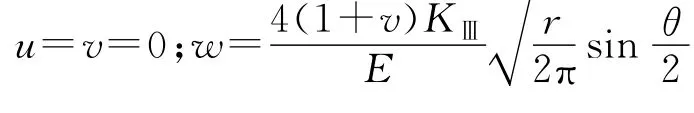
式中:KⅠ、KⅡ、KⅢ为3类裂纹的应力强度因子;r、θ为裂纹前缘极坐标,其中r→0时,也就是无限接近于裂纹前缘,上述位移场表达式才是准确解,而r>0时,也就是裂纹前缘附近,上述位移场表达式是近似解;u、v、w为直角坐标系x、y、z方向的位移分量;E为弹性模量;ν为泊松比,k=3-4ν。

由上述裂纹前缘附近位移场近似解表达式不难看出在求得裂纹前缘附近节点位移u、v、w后,就可由上述表达式求出应力强度因子KⅠ、KⅡ、KⅢ。一般情况下,采用2个裂纹面上对应节点的相对位移来求KⅠ、KⅡ、KⅢ,即令上述表达式中θ=π,可得KⅠ、KⅡ、KⅢ的表达式为:

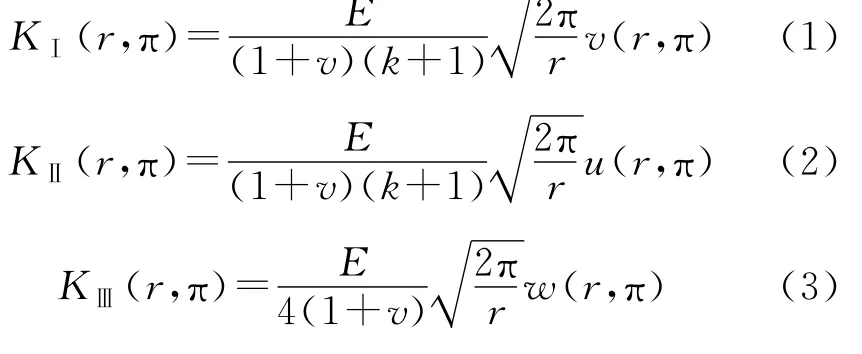
式中:u(r,π)、v(r,π)、w(r,π)为2个裂纹面上对应节点的直角坐标系x、y、z方向相对位移。

通过式(1)～(3)计算应力强度因子的方法就是位移外推法,而由于研究的带裂纹结构的日趋复杂,裂纹前缘的节点位移的计算已经不能通过解析解得到,而需要借助于数值方法,也就是说应力强度因子的计算需要采用数值方法,而现今求解应力强度因子首选的数值方法就是有限元法。

2 T型管节点的有限元模型

要采用有限元法计算管节点撑杆焊趾处穿透裂纹的裂纹前缘附近位移场,继而结合位移外推法计算裂纹前缘应力强度因子,首先要考虑的就是如何建立准确且高效的有限元计算模型。

由于是针对海洋平台导管架的管节点来研究,因而选取某导管架上典型尺寸的T型管节点来研究应力强度因子随裂纹前缘网格尺寸变化的收敛性,T型管节点的外形如图2,尺寸如表1。

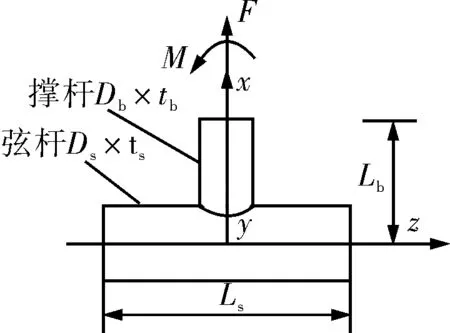
图2 T型管节点示意

表1 T型管节点外形尺寸

T型管节点的材料属性采用有代表性的导管架管节点用钢的参数:弹性模量E=206 GPa,泊松比ν=0.3。

对T型管节点施加的计算载荷分别为沿撑杆轴线方向的轴力F=312.78 N和管节点平面内的弯矩M=1 k N·m两类。

由于载荷和管节点结构都具有对称性,因而建立模型时只需利用对称性建立1/2模型,以提高计算效率,因而模型的约束条件为在模型的对称面上施加的对称约束和弦杆两端施加的固定端约束。

本文研究的裂纹是在T型管节点撑杆焊趾处穿透裂纹,裂纹对称地位于管节点冠点两边,在此裂纹长度半宽值由裂纹角度的半宽值代替,裂纹位置示意如图3,尺寸如图4。

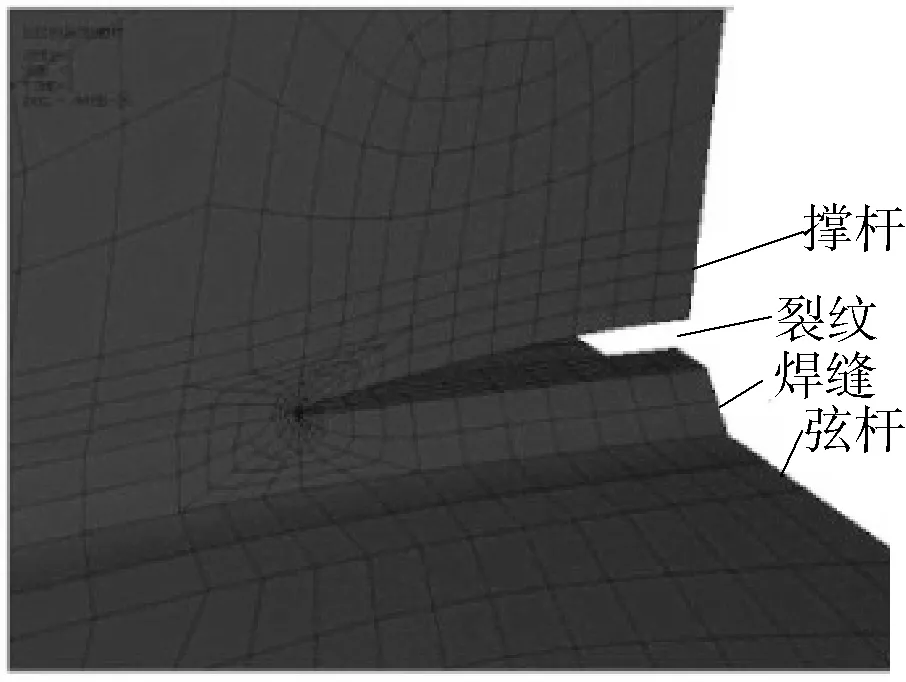
图3 裂纹位置示意

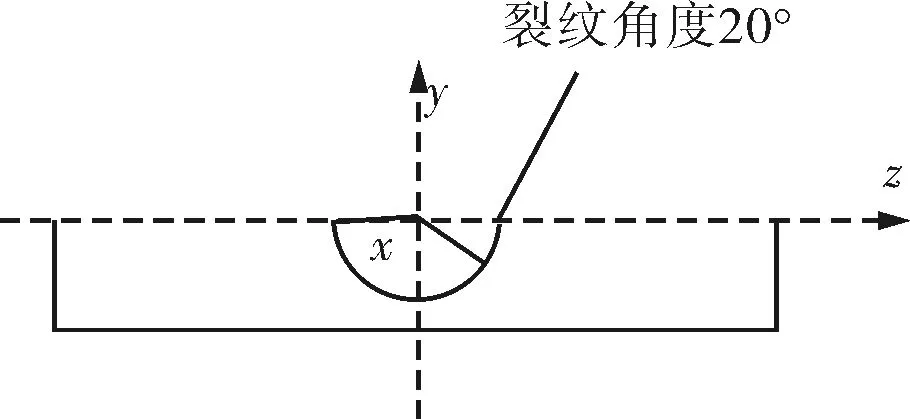
图4 裂纹尺寸

由于所研究的裂纹发生在焊趾处,凸起焊缝的存在势必对裂纹前缘应力强度因子解的有影响,在T型管节点模型中依据我国《钢结构焊接规范》[20]对焊缝的形状进行了模拟,如图5。

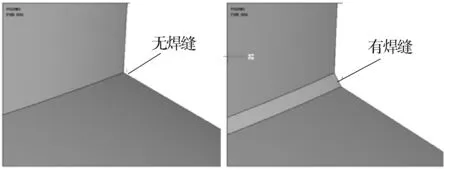
图5 焊缝示意

因为管节点焊趾处形状复杂,加载计算后有较大的应力集中,单元变形明显,因而管节点焊趾处裂纹的应力强度因子的解对于裂纹前缘及其附近的单元划分质量要求很高,这就要求裂纹前缘及其附近有着形状规整的有限元网格划分,对此将T型管节点的几何模型进行了独特的分区,如图6所示。

图6 几何模型分区(整体→局部)

基于以上的几何模型分区,采用ANSYS的实体单元对几何模型进行有限元网格划分。由于裂纹前缘存在奇异性问题,用普通单元模拟裂纹需要过多的自由度,即需要在裂纹前缘加密网格,这样不仅受到计算机能力的限制,而且解的收敛性与精度也没有保障。建议在裂纹前缘采用奇异单元,使单元本身位移模式反映奇异性,不仅降低了应力强度因子的解对裂纹前缘网格尺寸的依赖,而且解的精度也得到保证[21]。为此实体单元采用二阶二十节点的Solid186单元,以便于构造奇异单元,即将二阶单元的中间节点移动到靠近裂纹前缘的1/4点处,并且将20节点的六面体单元Solid186的1个面缩减为1条边而得15节点的五面体棱柱单元,由面缩减所得的边就是裂纹前缘,如图7所示。

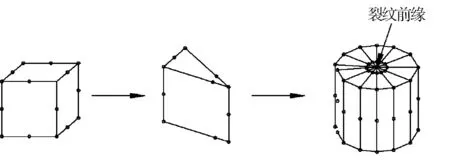
图7 转化solid186单元为奇异元

为了有效地减小模型的计算量,各部分网格尺寸划分的基本原则是应力梯度大的采用较小的尺寸,反之应力梯度小的采用较大的尺寸,因而由裂纹前缘奇异单元出发利用各个过渡分区,逐步增大网格尺寸,有限元模型如图8。

图8 T型管节点有限元模型

至此用于计算T型管节点撑杆焊趾处穿透裂纹的裂纹前缘应力强度因子的1/2有限元模型建立完成,此模型不但保证了焊缝周围尤其是裂纹前缘的计算精度,同时有效地控制了模型计算量。其他如K型、KK型等复杂管节点的此类问题亦可效仿以上分区网格划分方法建立有限元模型。

3 应力强度因子收敛性分析

经过分区网格划分方法建立撑杆焊趾处带穿透裂纹的T型管节点的有限元模型。为了验证ANSYS中计算所得的应力强度因子解对于裂纹前缘网格尺寸具有收敛性,又因为ANSYS的通用后处理器POST1采用位移外推法计算应力强度因子时只需要裂纹前缘奇异元的节点位移,因而仅对裂纹前缘的有限元模型采用了五个逐渐减小的网格尺寸,其中裂纹前缘奇异元的半径分别为5、4、3、2、1 mm,相对于撑杆厚度19 mm的比值在0.26～0.05,而其他区域网格尺寸不变,裂纹前缘区域有限元网格如图9。

图9 裂纹前缘不同网格尺寸

通过ANSYS通用后处理器POST1提取出裂纹前缘应力强度因子的结果,因为从3类应力强度因子结果幅值上看出所建立的混合型裂纹主要为I型裂纹,即张开型裂纹,因而在此仅给出轴力和平面内弯矩2种载荷下I型应力强度因子的结果,如图10～11。

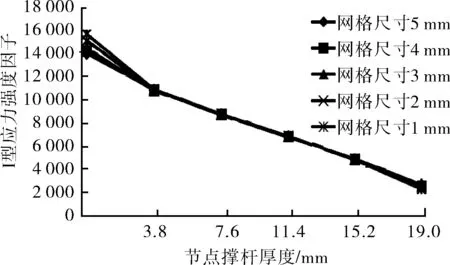
图10 轴力Ⅰ型应力强度因子

图11 平面内弯矩I型应力强度因子

在图10～11中,横坐标节点撑杆厚度0～19 mm指的是裂纹前缘沿撑杆厚度方向从外表面到内表面的6个节点的位置;图例中网格尺寸指的是裂纹前缘奇异元的半径大小。

由图10～11知,轴力和平面内弯矩2种工况计算出的不同裂纹前缘网格尺寸下的I型应力强度因子结果曲线重叠性很好,具体来说,每2个相邻网格尺寸下I型应力强度因子结果之间百分比差值的绝对值,轴力和平面内弯矩的结果均小于5%,尤其是裂纹深度方向上位于中间的4个节点的百分比差值均小于1%,这说明采用的分区域网格划分并且在裂纹前缘采用1/4节点奇异元的建模方法得到的应力强度因子结果对于裂纹前缘网格尺寸的变化具有收敛性,而且裂纹深度方向上中间段的结果较内外表面的结果有着更好的收敛性。

4 应力强度因子影响因素分析

验证了ANSYS计算的裂纹前缘应力强度因子随着裂纹前缘网格尺寸具有较好收敛性的基础上,在此进一步分析对应力强度因子有显著影响的管节点及裂纹尺寸因素。由于研究的是撑杆焊趾处穿透裂纹的应力强度因子,撑杆的壁厚势必对应力强度因子有显著影响,而裂纹角度半宽值可以反映裂纹扩展过程中应力强度因子的变化,因而着重研究薄壁管节点撑杆壁厚和穿透裂纹角度半宽值对裂纹前缘应力强度因子的影响。在保证其他模型参数均不变情况下,分别设置3个撑杆壁厚和3个裂纹角度半宽值,组合如表2。

表2 裂纹角度半宽值与壁厚组合

基于以上撑杆壁厚与裂纹角度半宽值组合,采用本文提出的建模方法建立了9个不同组合的T型管节点的有限元模型,并沿撑杆轴线方向施加轴力F=312.78 N,分别计算出应力强度因子,以提供比较。

4.1 裂纹角度半宽值对应力强度因子的影响

由图12～14可看出应力强度因子与裂纹角度半宽值正相关,这说明随着裂纹不断扩展,裂纹的扩展速度会不断增加,直至裂纹失稳扩展,因而对裂纹的处理要在裂纹初期就采取措施。

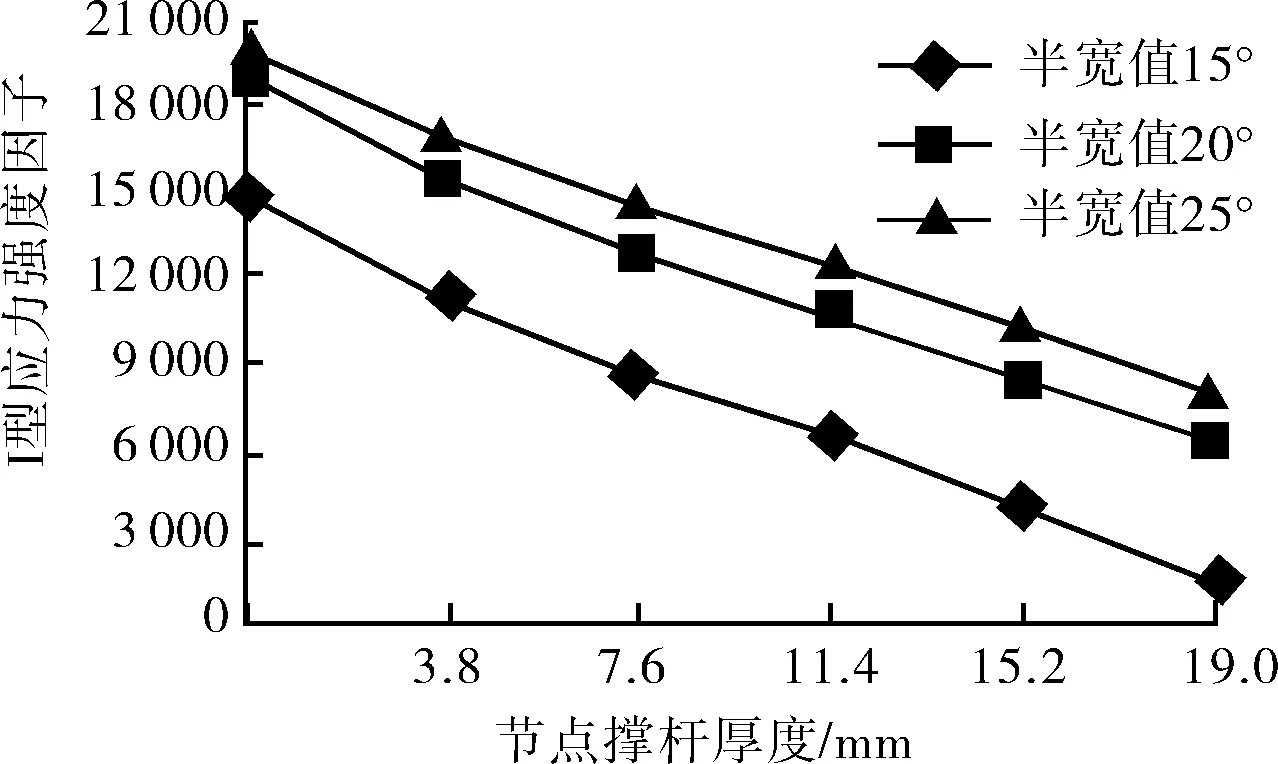
图12 组合1、2、3比较

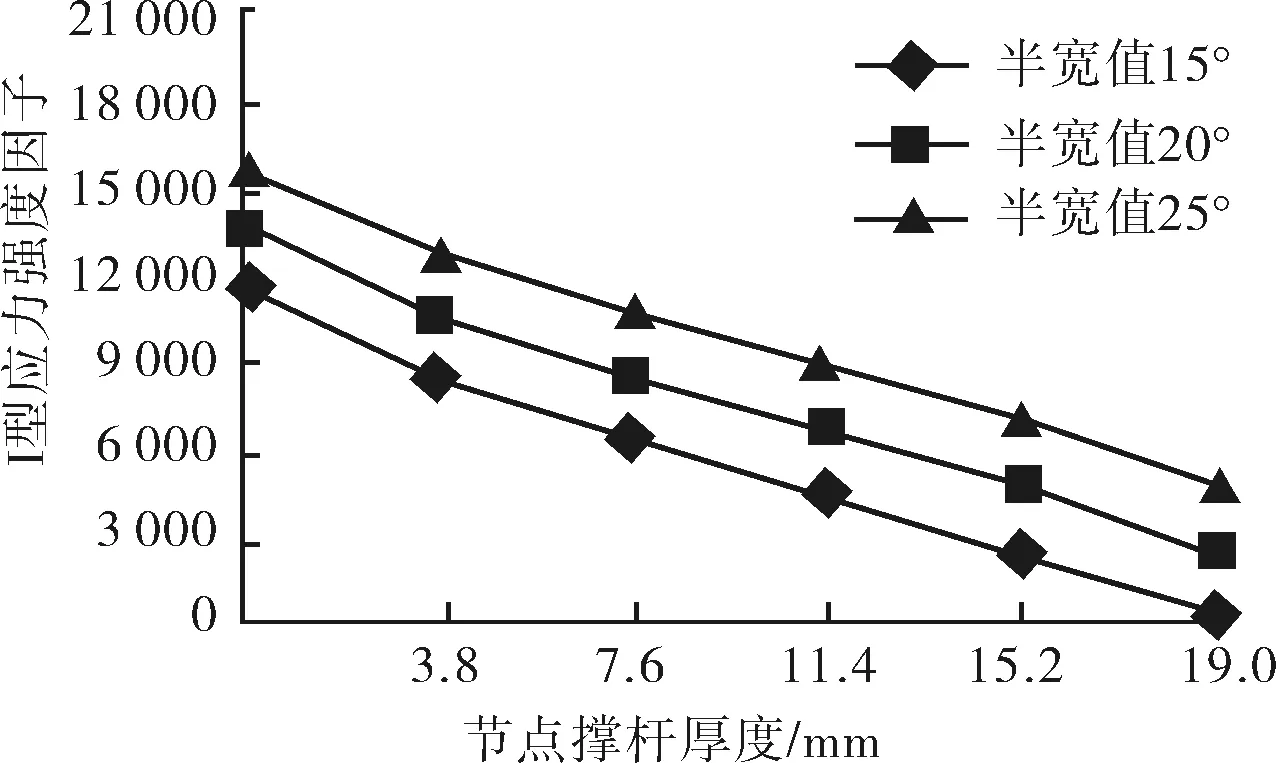
图13 组合4、5、6比较

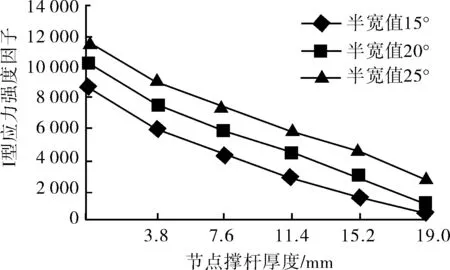
图14 组合7、8、9比较

4.2 撑杆壁厚对应力强度因子的影响

由图15～17可看出应力强度因子与撑杆壁厚负相关,也就是说要达到使管节点有更好的抗裂纹扩展能力,加大管节点焊缝处壁厚以及做好管壁防腐是有效措施。

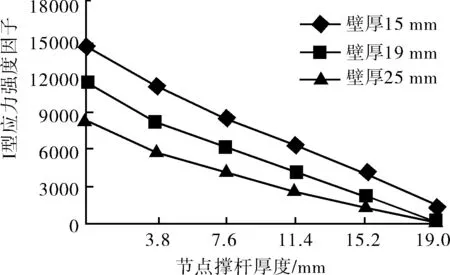
图15 组合1、4、7比较

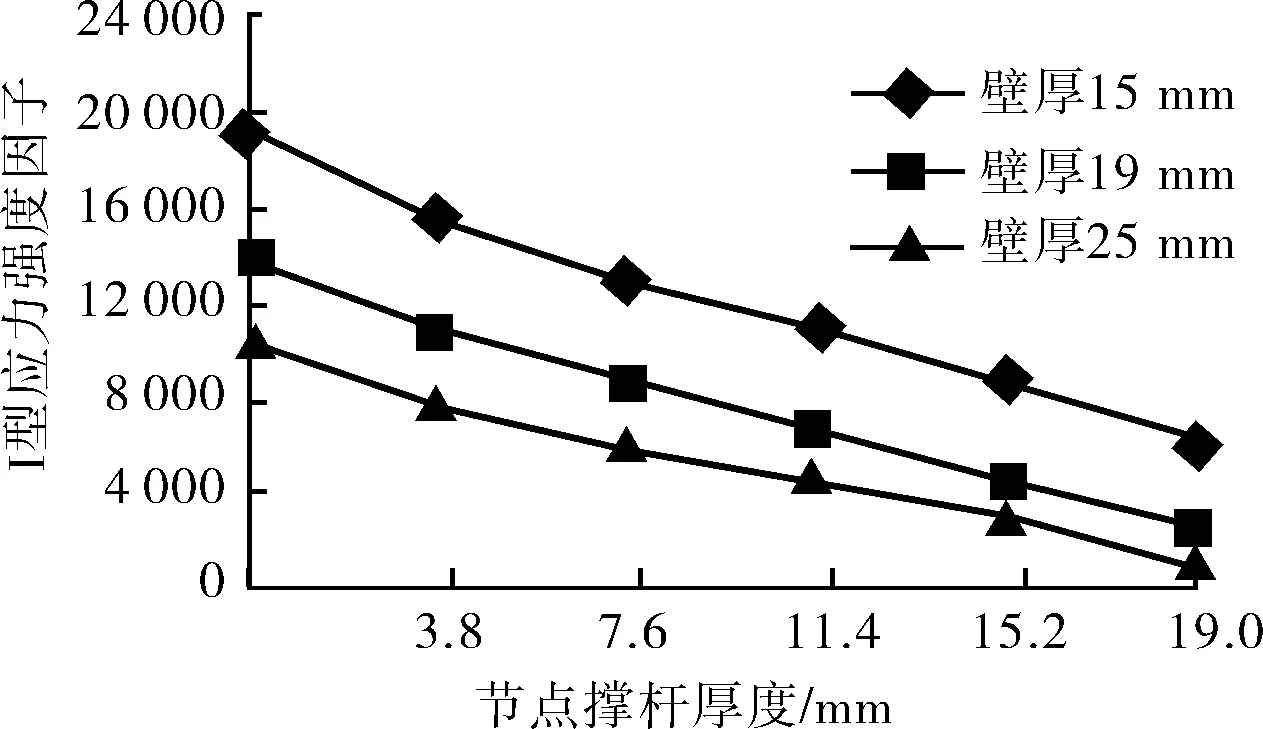
图16 组合2、5、8比较

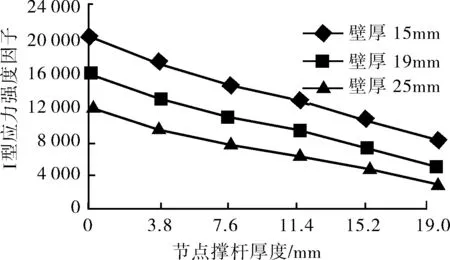
图17 组合3、6、9比较

5 结论

1) 本文提出了利用有限元软件ANSYS分区域划分网格并在裂纹前缘采用奇异单元的方法,建立的撑杆焊趾处带穿透裂纹的管节点有限元模型,既保证了计算的精度,又有效地减小了计算量。

2) 对5个裂纹前缘网格尺寸不同的T型管节点模型的应力强度因子计算结果的比较分析,证明了所提出的建模方法下建立的撑杆焊趾处带穿透裂纹的管节点有限元模型计算出的应力强度因子随裂纹前缘网格尺寸变化的收敛性。

3) 通过对9组不同撑杆壁厚和裂纹角度半宽值的T型管节点的有限元模型的应力强度因子计算结果的比较分析,得到了撑杆壁厚和裂纹半宽值对应力强度因子的影响规律。工程中对裂纹的处理工作要在裂纹失效破坏前,而且设计中应该加大管节点处壁厚以及做好管壁防腐。

[1] 张淑茳,史冬岩.海洋工程结构的疲劳与断裂[M].哈尔滨:哈尔滨工程大学出版社,2006.

[2] 李国义,郝丽丽,李箐泉.抽油杆杆体表面裂纹应力强度因子的研究[J].石油矿场机械,2007,36(12):14-16.

[3] Rooke D P,Cartwright D J.Compendium of Stress Intensity Factors[M].London:Her Majesty’s Stationary Office,1976.

[4] Tada H,Paris P C,Irwin G R.The Stress Intensity Factor Handbook[M].Hellertown:Del Research Corporation,1985.

[5] Murakami Y.Stress Intensity Factor Handbook[M].New York:Pergamon,1987.

[6] Kristiansen N O,Fu B.Free-surface stress intensity factor of surface cracks in tubular joint models[C]//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering.Glasgow,Scotland,Engl,1993:795-801.

[7] Nwosu D I,Olowokere D O.Evaluation of stress intensity factors for steel tubular T-joints using line spring and shell elements[J].Engineering Failure Analysis,1995,2(1):31-44.

[8] Caoa J J,Yanga G J,Packer J A,et al.Crack modeling in FE analysis of circular tubular joints[J].Engineering Fracture Mechanics,1998(61):537-553.

[9] Bahtui A,Tkach Y.Computational fracture mechanics assessment of 3-D crack-like defects in complex geometries[C]//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering.Rotterdam,Netherlands:2011:123-129.

[10] 钱仍勣,郑学祥,房咏柳.具有初始裂纹T型管节点的应力强度因子[J].海洋工程,1986,4(1):24-31.

[11] 卫欣,杨卫,余寿文.利用线弹簧模型计算含表面裂纹的板壳结构的复合型应力强度因子[J].计算结构力学及其应用,1991,8(3):257-265.

[12] 王自力,刘康林,李维扬.T型管节点表面裂纹应力强度因子的全三维有限元分析[J].哈尔滨工程大学学报,1995,16(2):31-37.

[13] 林红,陈国明,陈团海.老龄导管架平台管节点表面裂纹分析[J].机械强度,2008,30(5):814-819.

[14] 张宝峰,曲淑英,邵永波,等.海洋平台K型管节点的疲劳裂纹扩展分析Ⅰ:试验测试[J].计算力学学报,2007,24(5):643-647.

[15] 张宝峰,曲淑英,邵永波,等.海洋平台K型管节点的疲劳裂纹扩展分析Ⅱ:数值分析[J].计算力学学报,2007,24(6):800-805.

[16] 邵永波,杜之富,胡维东.海洋平台中KK管节点表面裂纹应力强度因子的有限元计算方法[J].船舶力学,2008,12(1):80-88.

[17] Lie S T,Chiew S P,Lee C K,Wong S M,Huang Z W.Modeling arbitrary through-thickness crack in a tubular T-joint[C]//Proceedings of the International Offshore and Polar Engineering Conference[C]//Seattle,WA,USA:2000:53-58.

[18] Lie S T,Lee C K,Wong S M.Model and mesh generation of cracked tubular Y-joints[J].Engineering Fracture Mechanics,2003(70):161-184.

[19] 程勒,赵树山.断裂力学[M].北京:科学出版社,2006.

[20] GB50661—2011,钢结构焊接规范[S].

[21] 解德,钱勤,李长安.断裂力学中的数值计算方法及工程应用[M].北京:科学出版社,2009.

Numerical Analysis of Stress Intensity Factor of
Through-Thickness Crack for Tubular T-Joints in Jackets

BAO Jing-fu1a,b,YANG Shu-geng1a,b,LI Duo2,ZHOU Nan2
(a.State Key Laboratory of Hydraulic Engineering Simulation and Safety;b.School of Civil Engineering,Tianjin University,Tianjin 300072,China;2.China Offshore Oil Engineering Corporation,Tianjin 300461,China)

A number of different sizes of finite element models of tubular T-joints in jacket platforms were established,using the finite element software ANSYS,with a through-thickness crack at the weld toe of the brace.The load was axial force and in-plane bending moment,applying on the brace.Displacement extrapolation method was used to calculate stress intensity factor at the crack front.Firstly,the astringency of the results of stress intensity factor calculated by ANSYS was verified,with variation of the mesh size at the crack tip.Secondly,the influence of the wall thickness of brace and the angle half-width of through-thickness crack on stress intensity factor was discussed preliminary.The variation of stress intensity factor was obtained,with the wall thickness of brace and the angle half-width of through-thickness crack,to make some suggestions for the crack arrest of tubular joints in engineering.

jacket platform;tubular joint;brace;through-thickness crack;stress intensity factor;finite element method

TE95

A

1001-3482(2014)02-0015-06

2013-08-27

薄景富(1988-),男,河北人,硕士研究生,研究方向:船舶与海洋结构物设计与建造,E-mail:tjubaojingfu@163.com。