DFFD自由变形算法实现过程

刘敏

(泉州财贸职业技术学校,福建泉州 362000)

DFFD自由变形算法实现过程

刘敏

(泉州财贸职业技术学校,福建泉州 362000)

本文主要从三维的Delaunay三角划分、三维Voronoi图和Sibson坐标值三个方面对算法进行全面分析。

自由变形算法 Delaunay三角划分 Voronoi图 Sibson局部坐标

1 三维Dirichlet算法概述

为了实现人脸夸张化变形,就必须在三维上进行变形,由于现今Dirichlet自由变形算法多应用于二维问题中,因此必须将其推广至三维上。我们可以对比其在二维时的Delaunay三角划分和Voronoi图形成来实现算法的三维推广。

首先,Delaunay三角划分时不再是划分为三角形,而是划分成四面体。其次,在形成Voronoi图时选取的是不再是三角形的外接圆圆心,而是四面体的外接球球心。最后,Sibson坐标的值是由中垂面切割后的体积与Voronoi单元体积之比。因此,算法总的步骤如下：

(1)设计控制点集合,从读入的物体点中选取控制点,不需要在控制点集合上定义任何特殊的拓扑结构。控制点可以在物体表面,也可以在物体的内部,但是物体需要变形的部分必须包含在控制点集合的凸包内。(2)对控制点进行三角划分,并保存三角划分所形成的四面体集合。对所有物体点遍历控制点的四面体集合,从而能够找到影响物体点的控制点集合,即为Sibson邻居。(3)对单个物体点的Sibson邻居(即影响它的控制点集合)进行三角划分,根据三角划分结果,计算物体所在Voronoi单元和Voronoi单元体积。(4)计算Sibson邻居划分物体点的Voronoi单元所形成的Voronoi图以及相应的体积,每个Sibson邻居划分求得的体积与物体点的Voronoi单元体积之比就是控制点相对于物体点的Sibson坐标值。(5)对所有物体点遍历(3),(4)操作,从而可以求出每个物体点的Sibson邻居的坐标值。(6)通过移动控制点,然后查找受影响的物体点,并根据Sibson坐标值计算受影响点的新坐标值,从而达到物体变形效果。

接下来,我们就按照上面步骤介绍如何在三维空间中进行Delaunay三角划分,以及如何形成Voronoi图,从而利用这些结果计算出Sibson坐标值。

2 三维Delaunay三角划分

我们依旧按照二维Delaunay三角划分的思想,采用超四面体的方法来进行三角划分。

首先,构造一个包含所有控制点的超四面体,通过遍历所有控制点找到其中含有x,y,z的最大值和最小值的点。然后通过以下公式构造点

在构造出超四面体之后,将进行依次插入点对其进行三角划分,生成三角网格。具体步骤如下：

(1)插入第一个点时,该点与超四面体的每一个面都形成一个四面体。记录这三个四面体,将其存储。(2)从第二点开始,插入点之后,判断此点在哪个四面体的外接球内,将相对应的四面体记录,并删除这些四面体中所包含的相同的面,从存储四面体的数据结构删除这些四面体。这样这些四面体去除相同面之后就形成一个多面体凸壳。(3)新插入的点与这个多面体凸壳的每个面都形成一个四面体,将这些四面体存储。(4)重复(2),(3)步骤,直到所有点都插入。然后删除超四面体和包含超四面体顶点的四面体,剩余的四面体集合即为控制点集合的三角划分结果。该结果主要用来确定物体点的Sibson邻居集合,即四面体的外接球包含该物体的四面体的顶点集合都为物体点的Sibson邻居。

3 三维Voronoi图

Voronoi图是为Sibson坐标的生成而铺垫的,它是Delaunay三角划分结果的对偶图。在二维的Voronoi单元中,其Voronoi边是由三角划分结果的三角形边的中垂线相交而成。Voronoi单元顶点则由这些中垂线的交点构成,这些顶点也是三角形外接圆的圆心。通过最简单的类比,我们可以知道,将一条线(A,B)放于三维空间中,要找距离A点比距离B点近的所有点,则可以找到这条线的垂直平分面,将空间划分为两块,包含A点的空间内的所有点到达A点的距离比到达B点的距离近。而对于点集S由n个点组成距离iP比距离其他点更近的点的区域是包含iP的那n-1个半空间的交集。这n-1个半空间是由点与其他点的垂直平分面确定的。所以,我们得知：三维空间中Voronoi图是一个多面体,多面体由三角划分结果的四面体棱经过其中垂面相交划分而得到的,四面体四条边的中垂面交点即为四面体外接球的球心,从而形成了Voronoi图的顶点。因此,Voronoi图是根据上步的Delaunay三角划分结果而得来。

在DFFD算法中,Voronoi图是用来求Sibson邻居坐标值的,根据公式

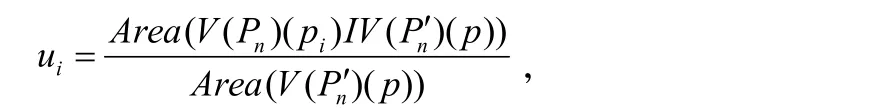
我们需要知道物体点所在的Voronoi单元的体积以及每个控制点划分得到的Voronoi单元的体积,相比即所谓的贡献比例。

首先讨论如何生成物体点所在的Voronoi单元。在得到三角划分结果后的具体步骤如下：

(1)通过物体点以及三角划分的结果,找到影响该物体点的控制点集合,即通过三角划分结果寻找其四面体的外接球包含物体点,这些四面体的顶点即为要找的控制点集合。(2)将这些控制点重新进行三角划分。根据三角划分的结果可以计算得到物体点的Voronoi单元。(3)重复(1),(2)步骤,则可以得到所有物体点的Voronoi单元。

通过类比二维Voronoi图我们可以知道：(1)共面的四面体的球心连线为Voronoi单元的一条棱;(2)共棱的四面体的球心共面,一次连接共棱的四面体的球心构成的面即为Voronoi单元的一个面。

3.1 物体点的Voronoi单元的形成

根据上面得到的Voronoi单元的棱和面的生成方法,可知物体点的Voronoi单元的形成过程,具体步骤如下：

(1)从物体点的Sibson邻居坐标中选取一点,设为pi,从保存Sibson邻居集合的三角划分结果的四面体所形成的凸包中(说明已经去掉重复面),找到包含该控制点pi的第一个面,将该面设为已用,并从该面中找到一条以pi为点的边pipj,将该面所在的四面体的外接球球心保存。(2)找到包含pipj边的另一个面,把该面设为已用,并把该面对应的四面体的外接球球心保存。(3)选择此面上以p为顶点的另一条边pipk。(4)重复(2),(3)依次找到包含pi的所有面,每个面对应一个四面体的外接球球心(因为是在凸包中,所以一个面只会对应一个四面体),依次连接这些球心可以形成一个多边形,这个多边形即为Voronoi单元的一个面。

3.2 控制点分割物体点的Voronoi单元

Sibson局部坐标值为控制点所分割物体点Voronoi单元所剩下部分的体积与物体点的Voronoi单元体积之比。现在我们就来介绍如何用控制点分割物体点的Voronoi单元。具体步骤如下：

(1)我们就随机选取一个控制点pi,以pi为顶点的棱E1设为

i pipj,使用下面方法求它的中垂面方程。由于我们已知pi的坐标为pj的坐标为。我们可以根据点法式来求垂直平分面,首先我们知道面的法线为且E1的中点为面上的点,设中点为s,其坐标为

3.3 通过Sibson坐标来变形

根据公式,可以求得控制点的Sibson的局部坐标值

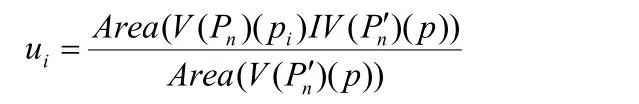
对于给定控制点集合 Pn和其凸包内的一点p的Sibson邻居集合计算出p相对于Pn的Sibson局部坐标当移动Pn中一个或多个控制点后,假设控制点的新位置为控制点pi的位移Δpi可以等于0,那么凸包内点 p的新位置P′就由来确定。

4 结语

本文介绍三维Delaunay三角划分的具体过程和三维Voronoi图的具体过程从而计算出Sibson局部坐标,通过细致的数学公式表达DFFD算法的实现步骤,从而实现了DFFD自由变形算法。

This paper is divided, three-dimensional Voronoi diagram and Sibson coordinate values ??of the three aspects of a comprehensive analysis of algorithms from the three-dimensional Delaunay triangulation.

free-form deformation algorithm Delaunay triangulation Voronoi diagram Sibson local coordinate

刘敏(1974.10.16-),性别:男,籍贯:江西丰城,学历:硕士,职称:高级讲师,研究方向:计算机应用。