一个新型指数混沌系统的设计与电路实现

薛 华

（滨州学院 光电工程系，山东 滨州 256603）

混沌可作为随机信号源用以产生保密通信中所需的伪随机序列.为了提高混沌伪随机序列的复杂性，近年来各种新型的混沌系统不断被提出，如超混沌系统［1－2］、分数阶混沌系统［3－4］、基于记忆电阻的混沌系统［5－6］、恒lyapunov指数混沌系统［7］等.非线性是系统产生混沌的必要条件之一，从某种意义上说非线性的强弱决定了混沌系统本身及其混沌吸引子的复杂性.迄今混沌系统中采用的非线性函数除乘积函数外，还有分段线性、绝对值及正弦等函数［8－10］.指数函数本身是一个非线性函数，如果把其指数变量用两个或两个以上的变量的乘积来表示，其将是一个强非线性项.另外，指数函数常作为人口成长模型，而PN结的数学模型也是一个自然指数函数.因此，如果自然指数函数能够构成混沌系统，其在实际应用中将比乘积项更有价值.但目前此类研究较少，因此作者拟提出用自然指数函数替代一个非线性乘积项来构建一种新型混沌系统，研究该系统的复杂动力学特性，同时还设计该混沌系统的硬件电路，通过数值仿真和电路实验验证该系统的混沌特性.

1 混沌模型

构造的新混沌系统为

其中：a，b，c∈R＋.

令

系统的5个平衡点为

通过分析可知，当系统参数a，b，c∈R＋，x2和y2为复数时，只有S0，S1，S2为系统的平衡点.当a＝10，b＝3，c＝4时，系统（1）存在一个混沌吸引子，如图1所示.

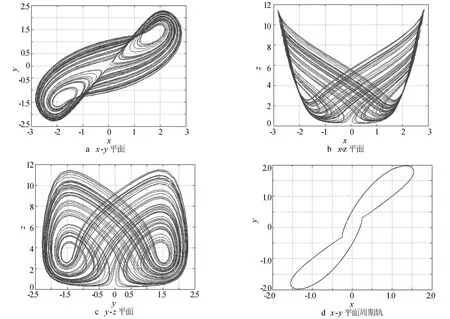
图1 系统（1）的混沌吸引子相图Fig.1 The chaotic attractor phase diagram of system（1）

2 基本动力学特性

2.1 系统的耗散性

系统（1）的散度为

当a＝10，b＝3，c＝4，－（a＋b－c）＜0时，系统为耗散系统，该系统按照如下指数速率收敛

系统被限制在一个体积为0的点集上，其渐进动力学行为被限制在一个吸引子上，说明该系统存在着吸引子.

2.2 平衡点及稳定性

当a＝10，b＝3，c＝4时，系统的3个平衡点为

在S0处将方程线性化，可得Jacobian矩阵

由其特征方程为｜J｜－λI＝0，得

在S0处，当a＝10，b＝3，c＝4时，系统（1）的特征根为

为使系统（1）产生混沌，特征方程的特征根要至少有一项大于零.当a＝3，b＝4，c＝10时，系统（1）的特征方程特征根λ2＝3.675 0＞0，由此可知平衡点S0不稳定.

在平衡点S1，S2处将方程线性化，得到二者相同的特征多项式

当a＝10，b＝3，c＝4时，线性化系统在S1，S2处的Jacobian矩阵具有相同的特征值

且满足Shil Nikov定理，则系统（1）能产生混沌的鞍焦点.

2.3 Lyapunov指数和分岔图

为了研究参数变化对系统动力学特性的影响，固定参数a＝10，c＝4，使参数b在［0，6］这个区间内变化，Lyapunov指数随b变化的指数图谱和变量x随b变化的分岔图如图2～3所示.

图2 Lyapunov指数谱Fig.2 Lyapunov index spectrum

图3 分岔图Fig.3 Bifurcation diagram

从图2可以看出，当a＝10，b＝1，c＝4时，LE1＝0，LE2＝LE3＜0，系统（1）处于周期状态.当b∈［2.3，3.2］，［3.5，6］，LE1＞0，LE2＝0，LE3＜0时，系统处于混沌状态，通过数值仿真可得到混沌吸引子相图（见图1）.

3 混沌系统的电路设计与实现

为了验证系统的混沌行为，基于模拟电子电路的设计原理，设计出了如图4所示的混沌电路［11］.该电路可实现加、减、反相、积分、指数运算，电路中的乘法器（AD633）可实现非线性乘积项，乘法器的增益为0.1［12］.

图4 系统（1）的混沌电路Fig.4 Chaotic circuit of system（1）

图4所示电路的状态方程为

设R4＝R11＝R17＝R，C1＝C2＝C3＝C.作线性变换

和时间线性变换

得

将上式改写为

当a＝10，b＝3，c＝4时，将式（1）与（10）比对，得到

令

可解得

根据图4所示的电路搭建硬件电路，通过示波器观察到的混沌吸引子如图5所示，此实验结果和Matlab仿真结果相同.

图5 示波器中观测到的混沌吸引子相图Fig.5 The chaotic attractor phase diagram that is observed in oscillograph

4 指数混沌序列随机性测试

为了了解指数混沌系统所产生的伪随机序列的随机性，采用NIST测试标准和安装在Linux系统下的STS－2.0软件包对其进行随机性测试.根据测试要求，利用该文提出的指数混沌系统生成了109bit的2进制序列，并将其分成1 000组进行测试，测试结果如表1所示.

表1 指数混沌伪随机序列测试结果Tab.1 Test results of the index chaotic pseudo－random sequence

根据P－VALUE值计算公式可得，若P－VALUE≥0.000 1，则可认为被测试序列P－VALUE值是均匀分布的.观察表1中15项测试的P－VALUE值，除了傅里叶变换测试项外，其余14项都满足判定要求，在测试中表现为均匀分布.

值得注意的是，虽然测试项在P－VALUE值和PROPORTION通过率中各有一项未通过，但一般情况下表1中前4项（基本测试项）通过即表明序列有良好的随机特性［13］，该测试中4个基本项在均匀分布和通过率方面都通过了测试，说明指数混沌有着良好的随机特性.

5 结束语

作者提出了一个新型的混沌系统，用指数函数替代原方程中的非线性项，该系统有复杂的动力学特性，理论上的动力学分析、数值仿真及实验都证明了系统具有混沌性，所设计的硬件电路选用的是反相输入运算放大器，使硬件电路的参数调节方便.指数运算电路是通过一个二极管实现，电路简单可行.该混沌系统通过了NIST测试，表明其有着良好的随机特性，因此可作为混沌信号源应用于混沌保密系统和混沌雷达系统之中.

［1］Lorenz E N.Deterministic non－perodic flows［J］.Atoms Sci，1963，20：130－136.

［2］Chen G，Ueta T.Yet another chaotic attractor［J］.International Journal of Bifurcation and Chaos，1999，9（7）：1465－1466.

［3］蔡国梁，谭振梅，周维怀，等.一个新的混沌系统的动力学分析及混沌控制［J］.物理学报，2007，56（11）：6230－6237.

［4］禹思敏.混沌系统与混沌电路－原理、设计及其在通信中的应用［M］.西安：西安电子科技大学出版社，2011：22.

［5］周小勇.一个新混沌系统及其电路仿真［J］.物理学报，2012，61（3）：030504.

［6］Wang G Y，Bao X L，Wang Z L.Design and FPGA implementation of a new hyperchaotic system［J］.Chinese Physics B，2008，17（10）：3596－3602.

［7］Wang G Y，Qiu S S，Li H W，et al，A new chaotic system and its circuit realization［J］.Chinese Physics，2006，15（12）：2872－2977.

［8］Stojanovski T，Kocarev L.Chaos－based random number generators－part I：analysis［J］.IEEE Trans Circuits Systems I，2001，48（3）：281－288.

［9］Stojanovski T，Pihl J，Kocarev L.Chaos－based random number generators－part II：practical realization［J］.IEEE Trans Circuits Systems I，2001，48（3）：382－385.

［10］Ding Q，Pang J，Fang J，et al.Designing of chaotic system output sequence circuit based on FPGA and its applications in network encryption card［J］.Int J of Innovative Computing，Information and Control，2007，3（2）：449－456.

［11］王光义，丘水生，等.一个新的三维二次混沌系统及其电路实现［J］.物理学报，2006，55（7）：3295－3301.

［12］韩春艳，薛华，吴新华.一个新的混沌模型及其数字伪随机信号的实现［J］.河北师范大学学报：自然科学版，2010，34（2）：165－169.

［13］Yalcin M E，Suykens J A K，Vandewalle J.True random bit generation from a double－scroll attractor［J］.TEEE Trans Cir Syst I，2004，51：1395－1404.