基于改进自适应遗传算法的固定结合面动态特性参数优化识别

朱坚民 张统超 李孝茹 周冬儿

上海理工大学，上海，200093

0 引言

数控机床存在大量的结合面，结合面的存在破坏了机床结构的连续性，增加了机床建模的复杂性。结合面的接触刚度和接触阻尼是机床刚度和阻尼的重要组成部分，统计表明，机床静刚度的30%～50%取决于结合面的刚度，机床阻尼的90%以上来源于结合面的阻尼，机床上出现的振动问题有60%以上来源于结合面，因此结合面对机床的静动态特性有重要影响［1－2］。建立合理的结合面动力学模型和获得准确的结合面动态特性参数一直是国内外相关学者研究的重点问题。

固定结合面是机床上最常用的一种结合面，主要为螺栓连接的结合面，起着固定连接和支撑的作用。目前，螺栓连接结合面的建模方法主要有粘接法、弹簧阻尼单元法和虚拟材料法等。基于弹簧阻尼单元的建模方法由于建模简单、满足工程实际要求而被广泛采用。王禹林等［3］采用弹簧阻尼单元模拟结合面的接触特性，建立了大型螺纹磨床的有限元模型并对其静动态特性进行了优化；曹定胜等［4］采用自定义的弹簧阻尼单元模拟加工中心结合面的刚度，对机床进行了理论模态分析和试验验证；冯砚博等［5］采用弹簧阻尼单元模拟结合面的性能，建立了多线切割机床的有限元模型并对其进行了动力学分析。以上研究在建模时将螺栓刚度和结合面的接触刚度叠加在一起由等效的弹簧刚度来代替，不符合结合面的实际情况，建模精度不高。结合面动态特性参数的识别方法主要有理论计算法、实验测试法和理论计算与实验测试相结合的方法。Fu等［6］提出了结合面刚度和阻尼参数的通用计算公式，但该理论计算法的可靠性较低；张华等［7］设计了滚动导轨结合面的试验台，通过消除基础位移法测得结合面的动态特性参数，但该实验测试法只能针对某些特定结构的结合面而通用性较差。理论计算与实验测试相结合的方法既发挥了理论分析的便捷性，又利用了实验测试结果的可靠性，因而得到了广泛的应用。陈新等［8］使用无约束优化问题的梯度法识别了磨床固定结合面的刚度和阻尼参数；王立华等［9］基于ANSYS软件的优化设计模块获得了铣床关键结合面的动态特性参数；黎定仕等［10］使用模拟退火优化算法识别了螺栓结合部的动力学参数，然而这些优化方法存在计算量大、收敛效率低等问题。

针对以上问题，本文以自行设计制作的螺栓连接固定结合面模型为研究对象，将螺栓和结合面的刚度分开考虑建立结合面的模型，提出一种改进的自适应遗传算法用于固定结合面动态特性参数的识别，获得了较高的识别精度。

1 固定结合面动态特性参数识别的基本原理

基于遗传算法的固定结合面动态特性参数识别的基本原理如图1所示，其基本思想是：①对固定结合面结构进行实验模态分析，获得其前若干阶固有频率、模态阻尼比和模态振型；②建立结合面结构的有限元模型，以结合面的刚度和阻尼参数为优化变量，以理论模态分析的固有频率和阻尼比与其对应实验模态分析结果的相对误差最小为目标函数，采用改进的自适应遗传算法对结合面有限元模型的刚度和阻尼参数进行寻优。

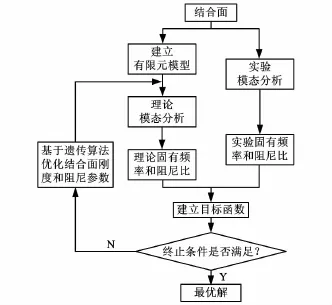
图1 基于遗传算法的固定结合面动态特性参数识别原理

2 固定结合面的建模方法

刚度和阻尼特性反映了固定结合面的本质属性，对于图2所示的由子结构M和子结构N组成的固定结合面，传统的建模方法是在结合面之间构造一组弹簧阻尼单元，若能合理确定弹簧阻尼单元与子结构的连接位置、弹簧阻尼单元的数量以及刚度和阻尼参数，则可用此等效的弹簧阻尼单元代替原固定结合面对子结构的作用，并可根据弹簧阻尼单元的串并联关系得出结合面的刚度和阻尼参数［11］。

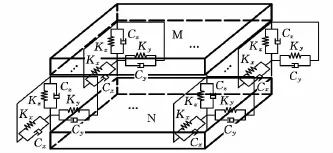
图2 固定结合面传统建模方法的等效模型

螺栓连接固定结合面的动态特性参数，包括x、y、z三个方向的刚度和阻尼。其中，刚度包括螺栓和结合面x、y、z三个方向的刚度，阻尼主要为由螺栓的预紧力引起的结合面在x、y、z三个方向的阻尼。因此，传统建模方法中的刚度实际是螺栓刚度和结合面刚度的叠加，该建模方法不能准确描述结合面的接触特性。本文在建模时将螺栓的刚度和结合面的接触刚度分开考虑，以提高理论模态分析的求解精度，进而保证结合面的参数识别精度。

本文在建立固定结合面模型时采用ANSYS13.0中提供的Matrix27单元，其特性和弹簧阻尼单元类似，通过设置刚度和阻尼参数使用Matrix27单元模拟螺栓的刚度和结合面的接触特性。在螺栓连接处，将子结构螺栓孔两端附近的节点利用耦合单元节点的方法连接到两个独立节点上，然后用Matrix27刚度单元将两独立的节点相连，如图3所示，每个刚度单元包含参数Kx1、Ky1、Kz1，分别代表螺栓x、y、z 三个方向的刚度。在接触面上，使用一定数量的Matrix27刚度单元和Matrix27阻尼单元将两子结构连接起来，用以模拟结合面的刚度和阻尼。每个刚度单元包含参数Kx2、Ky2、Kz2，每个阻尼单元包含参数Cx、Cy、Cz。根据 Matrix27单元的特性和并联弹簧阻尼单元的等效原理，从而求得固定结合面的刚度和阻尼参数。

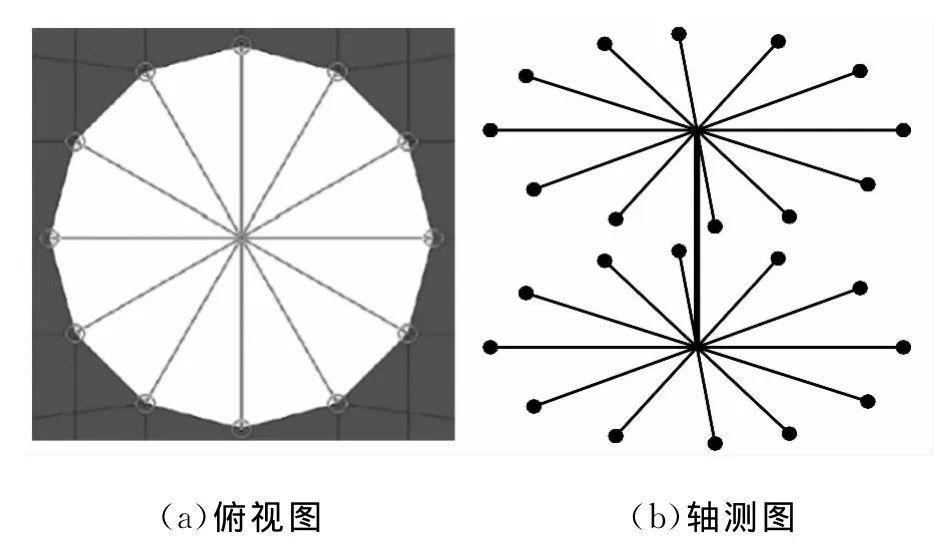
图3 螺栓的有限元模型

3 改进自适应遗传算法

遗传算法是一种模拟生物群体进化的高效并行的优化搜索算法。经典遗传算法和某些改进遗传算法的交叉概率和变异概率需要反复调整，且算法运行过程中的交叉概率和变异概率保持不变，导致算法局部搜索能力差、存在未成熟收敛等问题。

自适应遗传算法（adaptive genetic algorithm，AGA）由Srinivas等［12］提出，它的基本思想是交叉概率和变异概率随着适应度的变化而变化，采用相对某个解的最佳交叉概率和变异概率，算法具有较强的搜索能力和收敛能力。任子武等［13］提出了一种改进的自适应遗传算法（improved adaptive genetic algorithm，IAGA），该算法作了如下调整：如果个体的适应度接近平均适应度，则交叉概率和变异概率接近最大值；如果个体的适应度接近最大适应度，则交叉概率和变异概率很小。这种调整方法有利于进化后期优良个体的保存，但对于进化初期是不利的，因为一些适应度较好的个体处于一种几乎不变的状态，容易造成局部收敛。针对该问题，基于现有的自适应遗传算法，本文提出一种与进化代数相关的改进自适应遗传算法，其交叉概率和变异概率的调节公式如下：

式中，Pc为交叉概率，Pc1＝0.9，Pc2＝0.6；Pm为变异概率，Pm1＝0.1，Pm2＝0.05；F为待交叉的两个个体中适应度的较大值；F′为待变异个体的适应度值；Favg为当前群体的平均适应度值；Fmax为当前群体中适应度的最大值；n为当前迭代次数；N为最大迭代次数；λ为与进化代数有关的系数。

本文改进的自适应遗传算法的基本思想为：小于平均适应度的个体总是取较大的交叉概率和变异概率，有利于淘汰较差的个体；大于等于平均适应度的个体，其交叉概率和变异概率随着适应度的增大而减小，且随着进化代数的增加，交叉概率和变异概率越来越小。这种调节方法使得在进化初期适应度较大的个体可取到合适的交叉概率和变异概率，算法具有较强的全局搜索能力，随着进化代数的增加，算法的全局搜索能力减弱，局部搜索能力增强，便于找到全局最优解。

将上述改进的自适应遗传算法应用于固定结合面参数寻优时，刚度参数影响结合面结构的固有频率、模态振型和振动幅值，而阻尼参数不影响结合面结构的固有频率和模态振型，只影响振动幅值。在本文研究中，首先以结合面和螺栓的刚度参数为优化变量，在ANSYS中对结合面结构进行无阻尼实模态分析，基于本文改进自适应遗传算法寻优刚度参数；然后基于已识别的结合面刚度参数，以结合面阻尼参数为优化变量，在ANSYS中对固定结合面结构进行复模态分析，由改进自适应遗传算法寻优结合面阻尼参数。

改进的自适应遗传算法主程序采用MALTAB语言编制，在优化过程中动态调用由APDL语言编制的ANSYS模态求解子程序，改进的自适应遗传算法应用于结合面动态特性参数寻优的基本流程如图4所示。

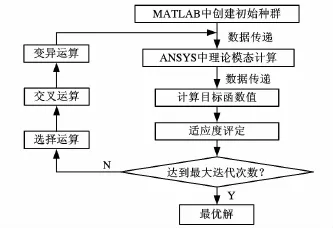
图4 基于改进遗传算法的固定结合面动特性参数寻优流程

在固定结合面动态特性参数优化识别过程中，需要考虑以下几点：

（1）优化变量。刚度参数识别时，变量为Kx1、Ky1、Kz1、Kx2、Ky2、Kz2，记为K；阻尼参数识别时，变量为Cx、Cy、Cz，记为C。

（2）目标函数。刚度参数识别时，以固定结合面固有频率的有限元计算值与其对应的实验测试值建立的优化目标函数如下：

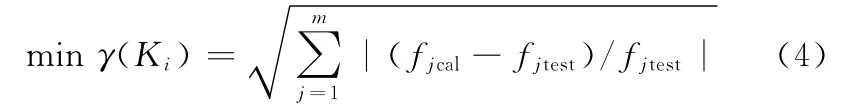
式中，fjtest为固定结合面第j阶的实验固有频率；fjcal为与实验固有频率相对应的理论固有频率。阻尼参数识别时，以固定结合面阻尼比的有限元计算值与其对应的实验测试值建立的优化目标函数如下：

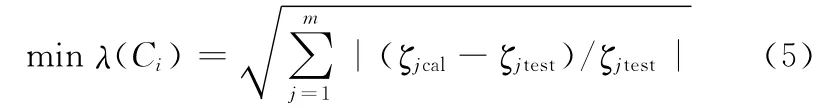
式中，ζjtest为固定结合面第j阶实验阻尼比；ζjcal为与实验阻尼比相对应的理论阻尼比。

（3）染色体编码方式。由于结合面刚度参数和阻尼参数的变化范围较大，使用二进制编码方式将使遗传算法不能兼顾编码精度和计算效率的要求。本文采用十进制浮点数对染色体进行编码，待识别的一组刚度或阻尼参数构成一条染色体，每一个基因位置对应一个待识别参数，如图5所示。

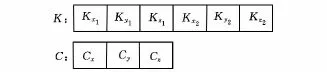
图5 染色体编码方式

（4）适应度函数。适应度函数用来评价个体的适应度，个体适应度越高，其存活的概率就越大。根据本文优化问题的目标函数（式（4）和式（5）），设置刚度参数识别时的适应度函数如下：

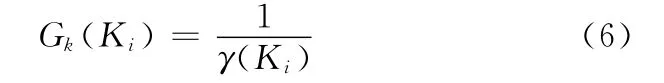
阻尼参数识别时的适应度函数如下：

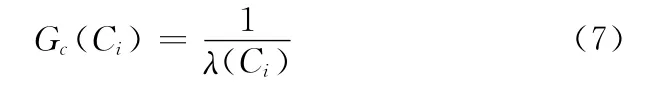
（5）遗传算子。选择算子采用赌轮盘选择与精英保留策略相结合的方法，个体按照与适应度成正比例的概率向下一代群体繁殖，如果子代最佳个体的适应度值小于父代最佳个体的适应度值，则将父代最佳个体直接复制到子代。交叉算子采用单点交叉的方法，并按式（1）确定交叉概率，对个体进行交叉操作。变异算子采用均匀变异的方法，并按式（2）确定变异概率，对个体进行变异操作。

（6）收敛准则。本文以设置进化代数终止遗传操作。

4 应用实例

4.1 固定结合面的物理模型

目前，机床上的螺栓连接固定结合面主要有三种形式：立柱与底座的结合面、滑块与滑板的结合面和导轨与床身的结合面，如图6所示。其中，立柱与底座的结合面、导轨和床身的结合面为“线性式”连接结合面，滑块与滑座的结合面为“阵列式”连接结合面，分别如图7a和图7b所示［14］。

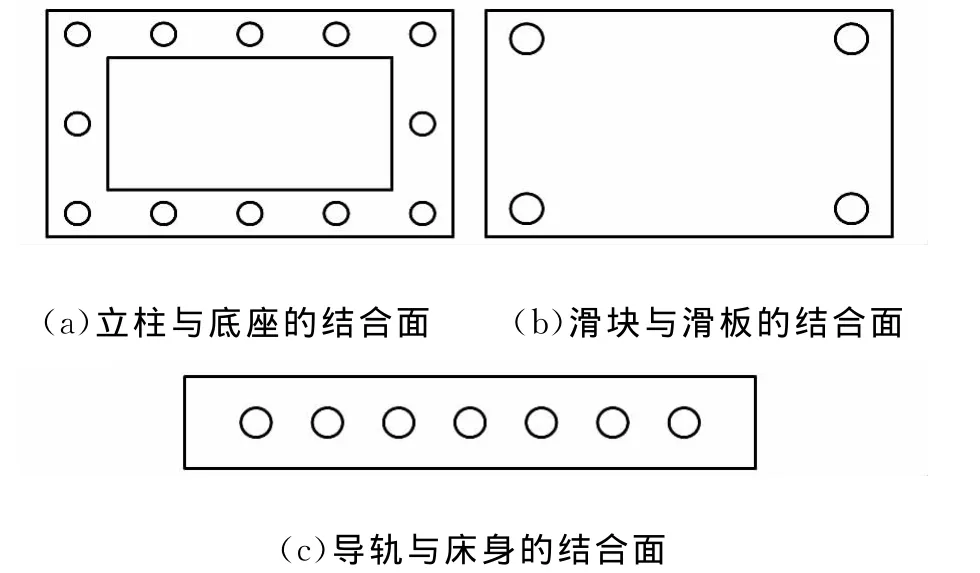
图6 机床固定结合面的三种形式

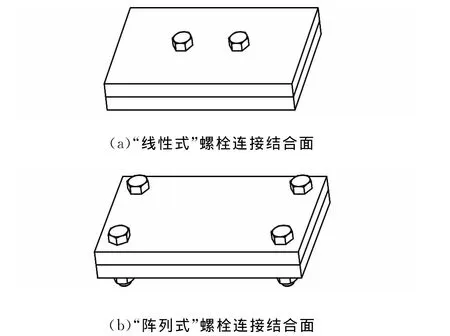
图7 “线性式”连接结合面和“阵列式”连接结合面

根据圣维南原理，连接螺栓的数量大于等于2且呈单列排布的结合面被称为“线性式”连接结合面，连接螺栓的数量大于等于4且呈阵列排布的结合面被称为“阵列式”连接结合面。国内外学者对“线性式”螺栓连接结合面已经进行了大量的研究［15－20］，而对“阵列式”螺栓连接结合面的研究较少。本文以“阵列式”螺栓连接结合面为研究对象，自行设计制作了结合面的物理模型，如图8所示。在该结合面物理模型中，上实验板和下实验板由4个位置对称的M12锁紧螺栓连接在一起，螺栓的强度等级为8.8级。上实验板的物理参数如表1所示，下实验板与上实验的物理参数相同，仅多了两个固定端用于实验时的安装固定。

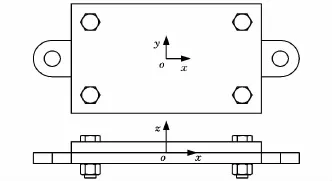
图8 “阵列式”螺栓连接固定结合面的模型

表1 结合面实验板的物理参数

4.2 固定结合面的实验模态分析

为了获得图8所示固定结合面模型的固有频率、阻尼比和模态振型，对其进行实验模态测试。实验中使用的测试设备主要包括Kistler SN2075427型激振力锤、3个BK 4525B型三向加速度传感器、搭载了3个NI 9234采集模块的NI cDAQ－9172数据采集系统、Exploit 135型力矩扳手。实验数据的采集和分析使用 Modal－View模态分析软件。

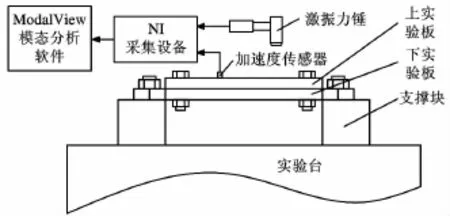
图9 模态测试系统原理图

图10 结合面的支撑方式

模态测试系统的工作原理如图9所示，实验时固定结合面的支撑方式如图10所示，结合面由两个支撑块支撑，通过T形螺栓连接固定在实验台上。T形固定螺栓的预紧力矩很大，可以认为结合面的支撑为刚性连接。如图11所示，在ModalView软件中建立结合面的模型，在该模型表面设置了24个测点，力锤锤击位置在第17号测点。使用单点激振多点拾振的锤击法对结合面进行模态测试，其基本过程主要为：对结构激振、输入输出信号的采集与处理、频响函数的计算和模态参数的识别。

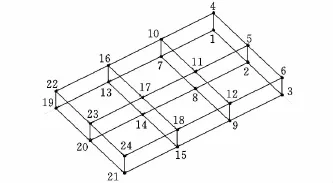
图11 实验模型及测点布置

结合面4个螺栓连接的预紧力矩为55N·m时，模态测试结果如表2所示。

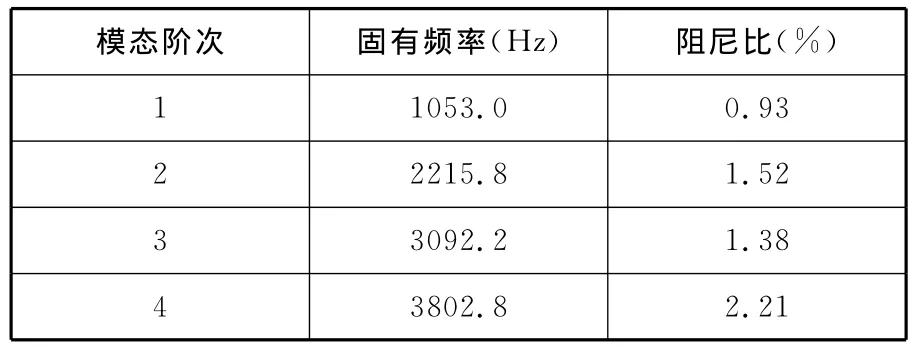
表2 实验模态分析结果

4.3 固定结合面的理论模态分析

在ANSYS13.0中建立固定结合面的有限元模型，如图12所示，该模型的节点数目为9032，单元数目为6116。在该有限元模型中，在螺栓连接处设置了4个Matrix27单元来模拟4个螺栓连接。在保证计算精度和效率的基础上，在结合面上通过均布的35个Matrix27刚度单元和35个Matrix27阻尼单元将上下实验板连接起来。根据刚度单元和阻尼单元的并联关系，该固定结合面x、y、z三个方向的刚度分别为35 Kx2、35 Ky2、35 Kz2，结合面x、y、z 三个方向的阻尼分别为35Cx、35Cy、35Cz。

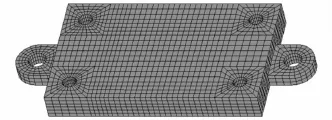
图12 固定结合面的有限元模型

根据实验模态测试时的实际约束情况，在结合面有限元模型两个固定端的底面施加了全约束。结合面刚度参数优化识别时，采用ANSYS中的Block Lanczos法进行模态求解。结合面阻尼参数优化识别时，采用ANSYS的QR Damped法进行模态求解。

4.4 寻优算法的有效性验证

为了验证本文优化算法的有效性，以图12中螺栓连接固定结合面的有限元模型为对象，用随机生成的若干组计算数据进行验证。随机设定3组螺栓和结合面的刚度参数Kx1～Kz2（表3中的“设定”行数据），代入有限元模型进行理论模态计算，将得到的前4阶理论固有频率f1～f4作为参考值代入式（4）建立目标函数，以螺栓和结合面的刚度参数Kx1～Kz2为优化变量，使用改进自适应遗传算法反向识别固定结合面刚度参数（表3中的“识别”行数据），如果识别值与设定值接近，则说明本文寻优算法是有效的。同理，对固定结合面阻尼参数进行验证的结果如表4所示。

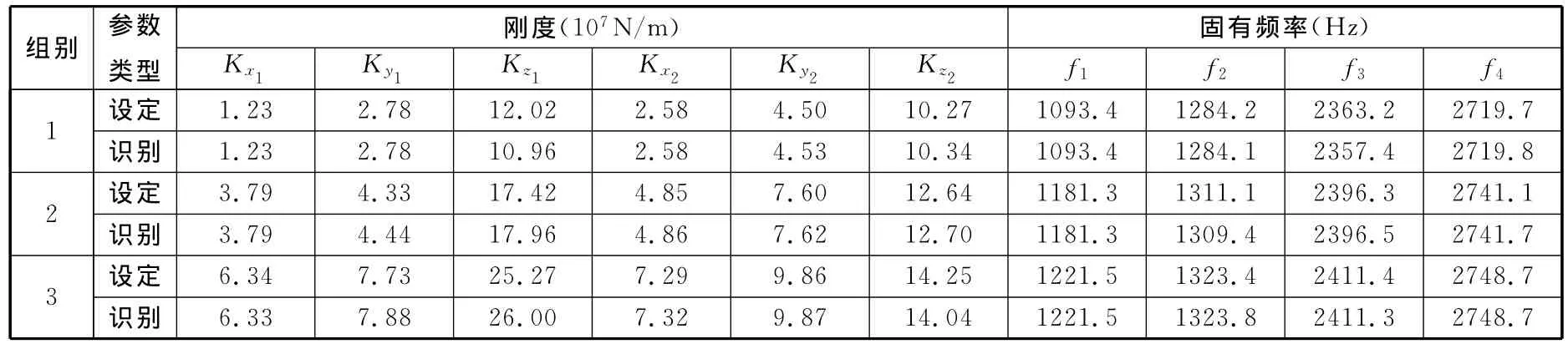
表3 刚度参数的设定值和识别值的比较

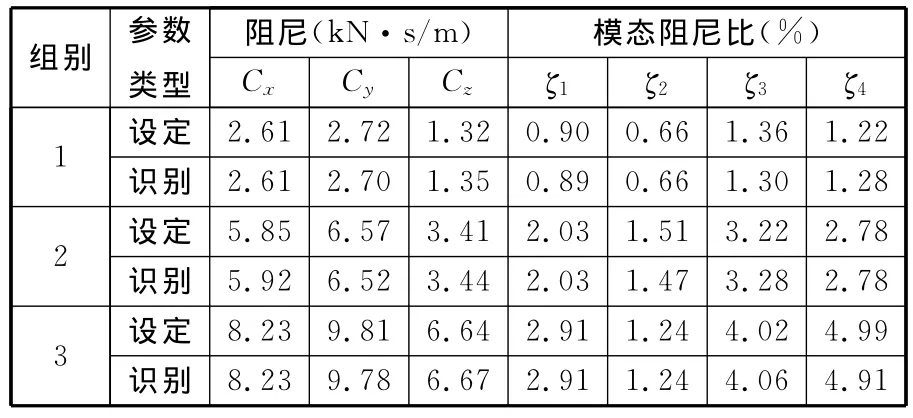
表4 阻尼参数的设定值与识别值的比较

表3和表4中，“设定”行数据是事先随机设定的刚度和阻尼参数，“识别”行数据是使用改进自适应遗传算法识别得到的刚度和阻尼参数。由表3、表4中的计算结果可以看出：使用本文改进自适应遗传算法识别的刚度和阻尼参数与真值（设定值）非常接近，误差很小，说明采用改进自适应遗传算法用于固定结合面动态特性参数的识别是可行的、有效的。

4.5 结合面刚度参数的识别

基于有限元分析的收敛性法则，以固定结合面待识别刚度参数为优化变量，对图12所示螺栓连接结合面有限元模型的前4阶固有频率进行收敛性分析，初步确定待识别固定结合面刚度参数的变化范围。

分析结果如图13所示，刚度参数从106N／m数量级开始改变5次到1011N／m数量级，每一次是上一次的10倍。螺栓连接固定结合面前4阶固有频率的计算值随着刚度变量的增加有收敛于某一确定值的趋势，当变量的数值超过109N／m数量级时，前4阶固有频率几乎不再变化。当刚度参数变化范围为107N／m数量级到109N／m数量级时，前4阶固有频率变化较为明显，在这一范围内种群个体的多样性较好，并根据结合面刚度参数的经验值设置其变化范围为107N／m数量级到1010N／m数量级。

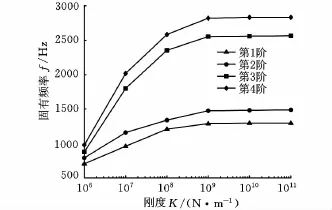
图13 固有频率的收敛性分析

在刚度参数的变化范围内，比较实验模态分析的振型和理论模态分析的振型，得出实验模态分析的第1、第2、第3、第4阶模态振型分别和理论模态分析的第1、第3、第5、第7阶模态振型符合较好，故由式（4）可得刚度参数优化识别的目标函数如下：

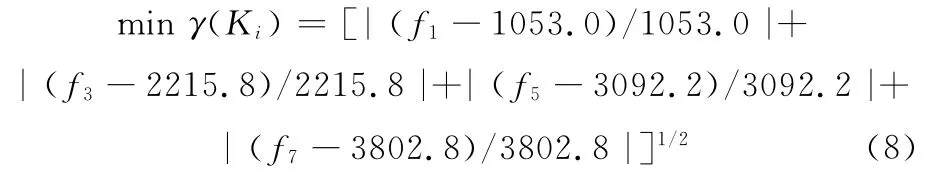
分别采用经典遗传算法（SGA）、文献［13］的改进自适应遗传算法（IAGA）和本文的改进自适应遗传算法对固定结合面刚度参数进行寻优，三种算法种群最优解的变化分别如图14a、图14b、图14c所示。由图14可知：采用SGA进行识别时，算法在70～80代时才能接近最优解，对应的目标函数最小值为0.3310；采用IAGA进行识别时，算法在40～50代时达到最优解，对应的目标函数最小值为0.3309；采用本文改进的自适应遗传算法进行识别时，算法在20～30代就已经达到最优解，对应的目标函数最小值为0.3309。采用本文优化算法时，最优解对应的螺栓和结合面的刚度参数如表5所示。

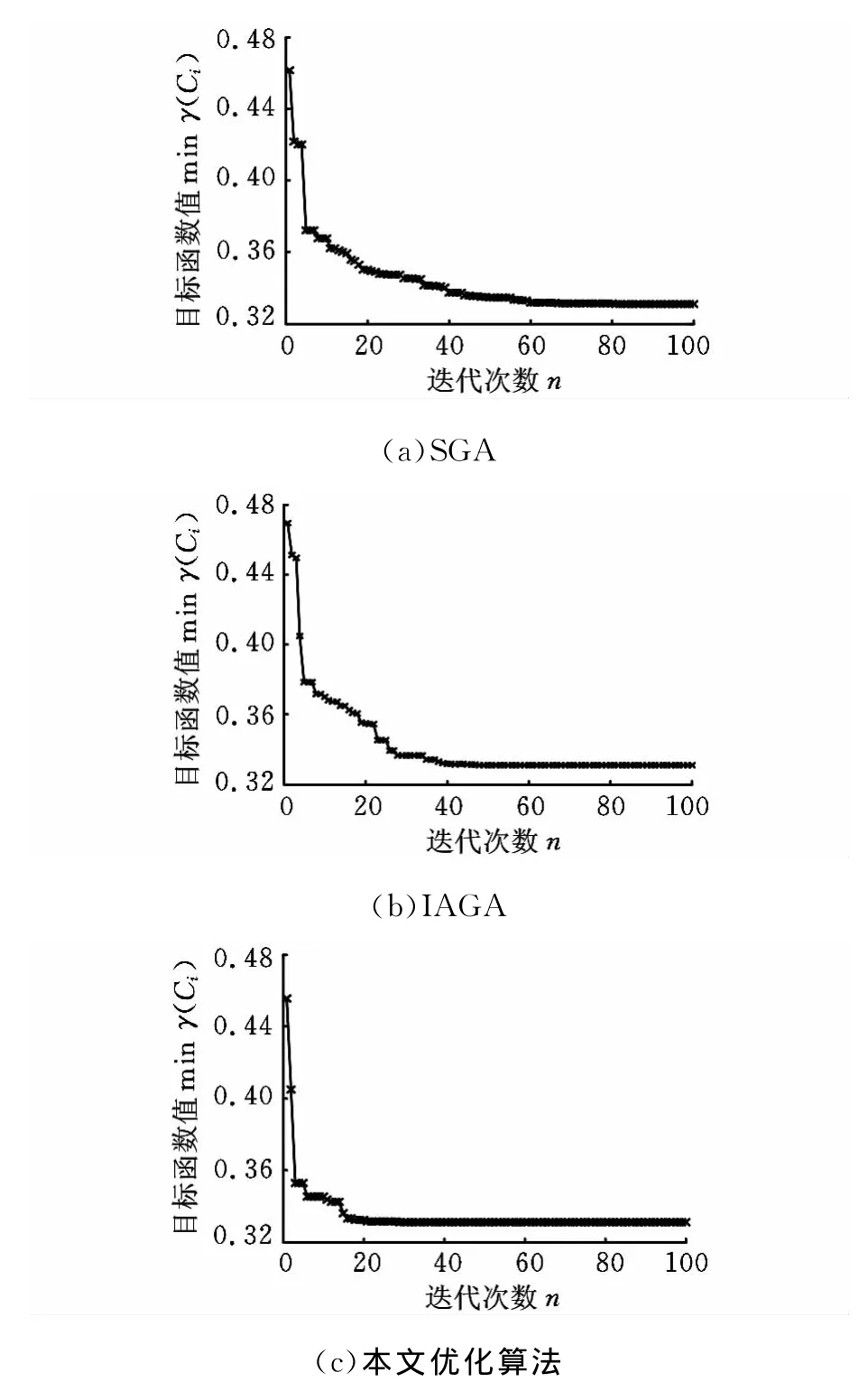
图14 刚度参数识别中最优解的变化

表5 刚度参数的识别结果 108 N／m

由表5中数据可知，螺栓x、y和z三个方向的刚度分别约为结合面三个方向刚度的5、7和5倍，螺栓的刚度和结合面的刚度相差较大，传统建模方法认为结合面刚度均匀分布将产生较大的建模误差，这验证了本文改进建模方法的必要性和正确性。在所识别的刚度参数条件下，结合面实验模态分析的固有频率和理论模态分析的固有频率如表6所示，实验模态振型和理论模态振型如图15所示。由表6中的数据可以看出，理论固有频率和实验固有频率误差均在5%以内，同时由图15中振型对比可知：理论振型和实验振型非常符合，验证了刚度参数识别的正确性。

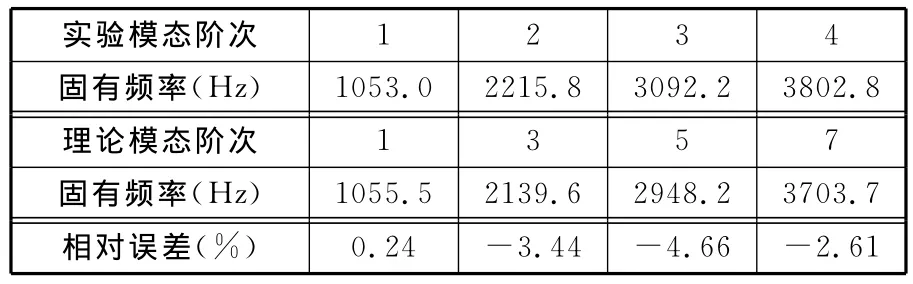
表6 实验固有频率和理论固有频率的对比

图15 实验模态振型与理论模态振型的对比

4.6 结合面阻尼参数的识别

将已识别的固定结合面刚度参数作为已知量，以结合面待识别的阻尼参数为优化变量，由式（5）可确定阻尼参数的优化目标函数：

分别采用经典遗传算法、文献［13］的改进自适应遗传算法和本文的改进自适应遗传算法对结合面阻尼参数进行寻优，三种算法种群最优解的变化分别如图16a、图16b、图16c所示。由图16可知：采用SGA进行识别时，算法在70～80代时才能接近最优解，对应的目标函数最小值为0.3079；采用IAGA进行识别时，算法在50～60代时达到最优解，对应的目标函数最小值为0.2960；采用本文的改进自适应遗传算法进行识别时，算法在30～40代就已经达到最优解，对应的目标函数最小值为0.2955。采用本文优化算法时，最优解对应的固定结合面的阻尼参数如表7所示。

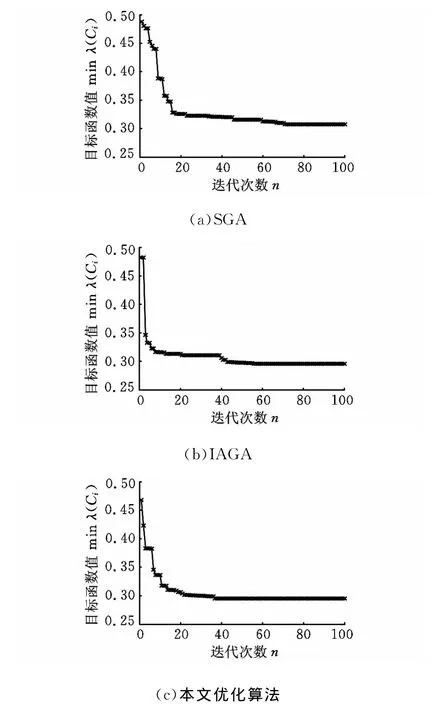
图16 阻尼参数识别中最优解的变化

表7 阻尼参数的识别结果 N·s／m

在所识别的阻尼参数条件下，结合面理论模态分析的阻尼比和实验模态分析的阻尼比如表8所示。由表8可以看出，理论模态分析的阻尼比和实验测试值误差均在5%以内，验证了阻尼参数识别的正确性。

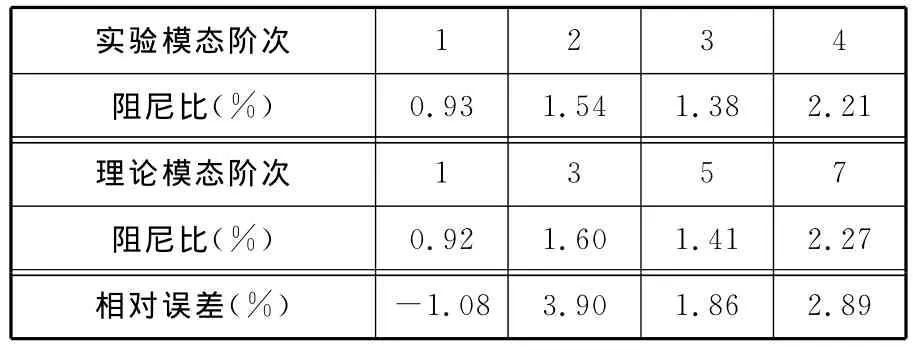
表8 理论模态阻尼比和实验模态阻尼比的对比

5 结论

（1）提出了在固定结合面建模中将螺栓和结合面的刚度分开考虑，在ANSYS中基于弹簧阻尼单元建立固定结合面有限元模型的方法，从而提高了固定结合面的建模精度。

（2）提出了与进化代数有关的改进自适应遗传算法，并将其应用于固定结合面动态特性参数的识别。对固定结合面刚度和阻尼参数识别的结果表明：与经典遗传算法和文献［13］的改进自适应遗传算法相比，本文提出的改进自适应遗传算法识别时间短、识别精度高。

（3）提出了基于遗传算法的固定结合面动态特性参数的识别方法，以有限元理论计算的固有频率和阻尼比与其对应实验模态分析结果的相对误差最小为优化目标函数，使用改进的自适应遗传算法优化识别固定结合面的刚度和阻尼参数，实际识别结果验证了本文方法的正确性和有效性。

（4）本文的方法适用于固定结合面的同时，也适用于机床导轨、丝杠、轴承等结合面动态特性参数的优化识别，可为机床整机理论分析提供准确的结合面参数，并为复杂机械结合面动态特性参数的识别提供参考。

［1］赵宏林，丁庆新，曾鸣，等.机床结合部特性的理论解析及应用［J］.机械工程学报，2008，44（12）：208－214.Zhao Honglin，Ding Qingxin，Zeng Ming，et al.Theoretic Analysison and Application of Behaviors of Machine Tool Joints［J］.Chinese Journal of Mechanical Engineering，2008，44（12）：208－214.

［2］张学良.机械结合面动态特性及应用［M］.北京：中国科学技术出版社，2002.

［3］王禹林，吴晓枫，冯虎田.基于结合面的大型螺纹磨床整机静动态特性优化［J］.振动与冲击，2012，31（20）：147－152.Wang Yulin，Wu Xiaofeng，Feng Hutian.Static and Dynamic Characteristics Optimization for a Whole Large－sized Thread Grinder Based on Joint Surface［J］.Journal of Vibration and Shock，2012，31（20）：147－152.

［4］曹定胜，王学林，张宏志.高速加工中心有限元计算模型与实验验证［J］.振动与冲击，2006，25（3）：190－192.Cao Dingsheng，Wang Xuelin，Zhang Hongzhi.FE Model and Experimental Verification for Machine Center Modal Analysis［J］.Journal of Vibration and Shock，2006，25（3）：190－192.

［5］冯砚博，孙涛.多线切割机床动力学分析［J］.振动与冲击，2011，30（7）：169－172.Feng Yanbo，Sun Tao.Dynamic Analysis of Multi Wire Saw［J］.Journal of Vibration and Shock，2011，30（7）：169－172.

［6］Fu Weiping，Huang Yumei，Zhang Guangpeng.Experimental Investigation on Damping Behavior of Normal Joint Surfaces at Unit Area［J］.Modeling，Measurement ＆Control，B，1993，51（2）：13－20.

［7］张华，袁军堂，汪振华.滚动导轨结合面动态特性参数识别实验研究［J］.中国机械工程，2011，22（4）：415－418.Zhang Hua，Yuan Juntang，Wang Zhenhua.Experimental Research on Identification of Dynamic Characteristic Parameters of Rolling Guide’s Joint［J］.China Mechanical Engineering，2011，22（4）：415－418.

［8］陈新，孙庆鸿，毛海军，等.基于接触单元的磨床螺栓连接面有限元建模与模型修正［J］.中国机械工程，2001，12（5）：524－526.Chen Xin，Sun Qinghong，Mao Haijun，et al.Modeling and Correcting FEM with Contact Element forthe Combined Surfaces of Grinder Bolts［J］.China Mechanical Engineering，2001，12（5）：524－526.

［9］王立华，罗建平，刘泓滨，等.铣床关键结合面动态特性研究［J］.振动与冲击，2008，28（8）：125－129.Wang Lihua，Luo Jianping，Liu Hongbin，et al.Research on Dynamic Characteristics of Key Machine Joint Surfaces of the Numerically Controled Milling Machine［J］.Journal of Vibration and Shock，2008，28（8）：125－129.

［10］黎定仕，张以都，王鹏.基于结构阻尼的机械结合部动力学模型研究［J］.振动与冲击，2010，29（8）：204－208.Li Shiding，Zhang Yidu，Wang Peng.Dynamic Model of Machine Joints Based on Structure Damping［J］.Journal of Vibration and Shock，2010，29（8）：204－208.

［11］Yoshimura M，Okushima K.Computer－aided Design Improvement of Machine Tool Structure Incorporating Joint Dynamics Data［J］.Annals of the ICRP，1979，28（1）：241－246.

［12］Srinivas M，Patnailk L M.Adaptive Probabilities of Crossover and Mutation in Genetic Algorithms［J］.IEEE Transaction on System，Man and Cybernetics，1994，24（4）：656－667.

［13］任子武，伞冶.自适应遗传算法的改进及在系统辨识中应用研究［J］.系统仿真学报，2006，18（1）：41－43.Reng Ziwu，San Ye.Improved Adaptive Genetic Algorithm and Its Application Researchin Parameter Identification［J］.Journal of System Simulation，2006，18（1）：41－43.

［14］Mao Kuanmin，Li Bin，Wu Jun，et al.Stiffness Influential Factors－based Dynamic Modeling and Its Parameter Identification Method of Fixed Joints in Machine Tools［J］.International Journal of Machine Tools ＆ Manufacture，2010，50（2），156－164.

［15］Heller L，Foltete E，Piranda J.Experimental Identification of Nonlinear Dynamic Properties of Built－up Structures［J］.Journal of Sound and Vibration，2009，327（1）：183－196.

［16］Jalali H，Ahmadian H，Mottershead J E.Identification of Nonlinear Bolted Lap－joint Parameters by Force－state Mapping［J］.International Journal of Solids and Structures，2007，44（25／26）：8087－8105.

［17］Tian Hongliang，Li Bin，Liu Hongqi，et al.A New Method of Virtual Material Hypothesis－based Dynamic Modeling on Fixed Joint Interfacein Machine Tools［J］.International Journal of Machine Toolsand Manufacture，2011，51（3）：239－249.

［18］温淑花，张宗阳，张学良，等.固定结合面刚度分形模型［J］.农业机械学报，2013，44（2）：255－260.Wen Shuhua，Zhang Zongyang，Zhang Xueliang，et al.Stiffness Fractal Model for Fixed Joint Interfaces［J］.Transactions of the Chinese Society for Agricultural Machinery，2013，44（2）：255－260.

［19］李玲，蔡安江，蔡力钢，等.栓接结合部动态特性辨识方法［J］.机械工程学报，2013，49（7）：168－175.Li Ling，Cai Anjiang，Cai Ligang，et al.Identification Method for Dynamic Properties of Bolted Joints［J］，Chinese Journal of Mechanical Engineering，2013，49（7）：168－175.