基于能量法的脑机接口运动想象分类研究

【作 者】乔静，胡鹏举，洪杰

1 西北工业大学机电学院，西安市，710072

2 中国航天空气动力技术研究院研究生院，北京市，100074

0 引言

脑机接口(Brain-computer Interface，BCI)，是近些年来发展起来的一种人机接口技术，它不同于以往传统的依靠键盘、鼠标等外围设备与计算机进行交互的方式，是一种不依赖于脑的常规输出通道(即外围神经和肌肉)就可以实现脑—机通信的系统[1]，该技术为有运动障碍的人提供了新的与外界沟通的途径。由于脑电信号(EEG)记录简单，且外置式无创伤性，对被试的安全及要求比较低，多数BCI技术都基于EEG信号。

经过各国研究者的努力和实践，目前，已经形成具有代表性的用以实验、验证的BCI系统：事件相关电位(Event Related Potential: ERP)P300的BCI系统[2]、视觉诱发电位(Visual Evoked Potential: VEP)的BCI系统[3]、事件相关同步/去同步 (Event-related synchronization and desynchronization,ERS/ERD)的BCI系统[4-6]、稳态视觉诱发响应(Steady State VEP:SSVEP)的BCI系统[7]等。为后续研究者提供了实验建立的基础和信号特征提取、分类的依据，目前常见的EEG信号分析技术有：时域分析法、频域分析法、时—频分析法及多维统计分析法。其中，时域分析法直观性强，能通过时域图明显表示出随时间变化而引起的信号变化，不失为一种直观有效的EEG信号分析方法，最初的EEG信号分析大都采用这种方法；时—频分析法可以将信号的时间和频率特征同时显现在一幅图里边，表现不同时间点的信号频率变化，更有利于凸显EEG信号的特性，所以在EEG信号的处理中得到广泛应用，是目前比较成熟的EEG信号分析方法[8-9]。

将EEG信号作为BCI系统的输入，要先确定所需EEG信号的特征，在本文的研究中，需要选择与运动最相关的脑电节律。脑科学的研究表明，人类脑电频率主要分布在0.5～30 Hz，划分为4个基本节律：δ节律0～3 Hz、θ节律3～8 Hz、µ节律8 ～13 Hz和β节律13～30 Hz。脑科学经过这么些年的发展，已经证实：当人们想象或做单侧肢体运动时，大脑神经元突触后电位相互削弱和增强，使大脑对侧的运动感觉区的µ节律和β节律能量减小，而同侧的运动感觉区µ节律和β节律能量增大，这种现象被称为事件相关去同步(ERD)和时间相关同步(ERS)[4]。脑电信号的ERD和ERS现象成为判断左右手想象运动的最根本依据[10]。

目前，常见的基于运动想象的EEG信号的特征提取算法有：小波变换、支持向量机、傅里叶变换（Fast Fourier Transform，FFT）、相关性分析、AR参数估计、共空间模型（CSP）、Butterworth低通滤波、遗传算法等；常见的基于运动想象的EEG信号的分类算法有：线性距离判别、支持向量机（Support Vector Machine，SVM）、聚类算法、贝叶斯分类器、人工神经网络(Artificial Neural Networks,ANN)等[11-17]。

本文针对6路EEG信号通道、两类思维任务的实验平台，采用小波包分解的方法提取特定频带的能量信息，然后采用线性距离判别的方法进行分类，最后采用Kappa系数进行分类衡量，编程简单，得到良好的实验结果。

1 实验数据

本研究所用的实验数据来自公开发布在互联网的用于BCl2008竞赛的脑电数据，是由奥地利Graz科技大学提供的BCICIV_2b_gdf，分为训练数据和测试数据。整个试验共有9个被试者，每个被试者做5组试验，其中前2组实验是无反馈的，后3组实验是带反馈的；前3组是训练数据，后2组是测试数据。每个实验包括120个试次（60次想象左手，60次想象右手）。实验采用AgCl电极，数据由差分电极从国际标准10-20导联系统的C3、CZ、C4三个通道获得，如图1所示。依据人体功能区域在脑部的划分，C3、C4位置包含了想象对侧手部运动时最为丰富的信息，本研究只采用这两个通道的数据信息。实验组成如图2所示。

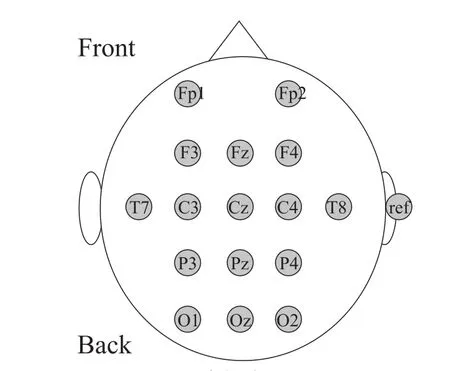
图1 电极布置图Fig.1 Position of EEG electrodes

图2 实验设置时序图Fig.2 Timing of the paradigm

实验设置1中，1～3 s，受试者盯着屏幕，屏幕上显示一个“+”，其中第2 s时，一声蜂鸣(1000 Hz，70 ms)，提示试验即将开始。3 s时十字符号被一个向左或者向右的箭头所代替，受试者被箭头引导着想象手的运动，该箭头持续1.25 s，整个实验过程持续7 s，之后有一个1.5 s的暂停，最后有1 s的空白，防止与接下来的试次发生重叠。

实验设置2中，实验开始时屏幕上呈现灰色的反馈标示，第2 s时一声蜂鸣(1000 Hz，70 ms)提示试验即将开始。3 s时箭头出现并持续至第7.5 s，受试者依据箭头指向想象相应的运动，在反馈阶段，反馈标示依据想象结果与箭头对应或不对应而呈现笑脸或苦脸。同样在之后有一个1.5 s的暂停和1 s的空白，防止与接下来的试次发生重叠。

2 特征量的提取和分类

2.1 数据预处理

选择每个被试的前3组实验作为训练数据进行特征提取和分类器训练，后2组实验用来测试分类器。

选择合适的频段进行滤波：依据运动想象左右手的µ节律8～12 Hz和β节律19～26 Hz[4]，对数据进行巴特沃斯带通滤波。在构建带通滤波器时，首先会牵涉到滤波器阶数选择的问题。阶数越高，滤波器的截止频率越精确，但会导致在时域的数据分散；阶数太低了，滤波效果不明显[18]。经过多次试验，本文选用6阶的巴特沃斯带通滤波。

图3 想象左右手(5 ～7)s数据滤波前后对比Fig.3 Data comparison of (5 ～7)s about left/right hand class before and after filtering

选择合适的时间段作为能量对比区间：对每组数据都进行可视化处理，然后根据计算的结果，最终选择(5 ～7)s作为能量特征对比区间。其滤波前后结果，如图3所示。

2.2 小波包分解

小波包分解是小波变换的一种形式，小波变换是时间（空间）频率的局部化分析，它通过伸缩平移运算对信号(函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能很好地反映信号在时域和频域的局部信息。

信号f (x)从 j尺度到 j+1尺度逐步分解的过程，也就是对信号f (x)从高分辨率到低分辨率的分析过程[13-14]。

小波包分解的数学公式为：

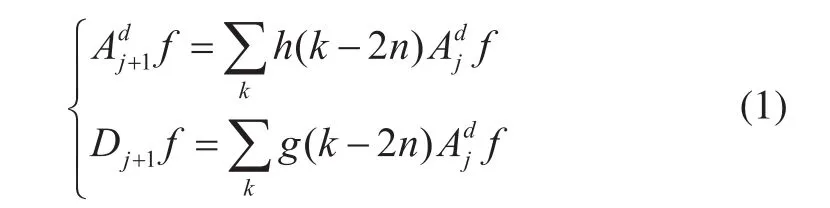
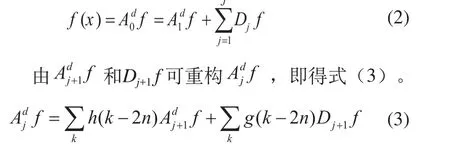
小波包分解是一个递推的过程，分解形式及过程，如图4所示。其中CA、CD分别表示小波包分解所得各层的逼近信号(低频部分)和细节信号(高频部分)。

小波包分解的级数是由用于特征提取的信号所覆盖的频率范围决定的，分解级数越高，各层所覆盖的频率范围越小[14,19]。因此，将信号进行小波包分解时，分解的层数要视具体信号的采样频率及用于特征提取的信号的频率范围而定。本文分析所采用的脑电竞赛数据的采样频率为250 Hz，先将信号进行重采样到256 Hz，然后进行5层分解，各层所对应的频带如表1所示。

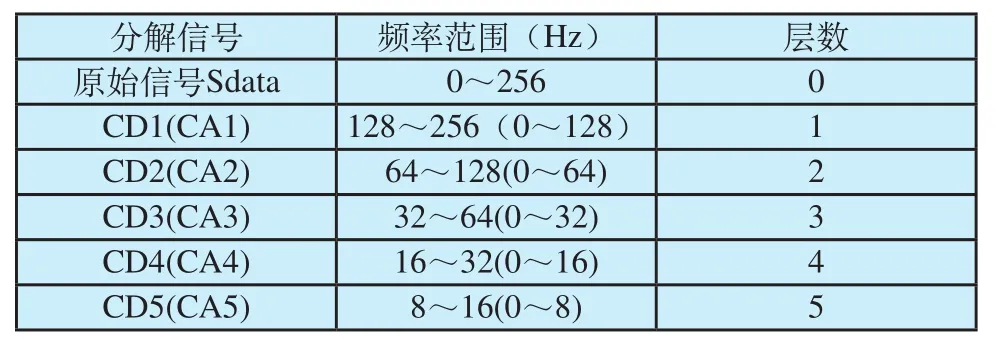
表1 分解层数与对应频率Tab.1 Decomposition levels and the corresponding frequency bands

图4 小波包分解示意图Fig.4 Schematic diagram of wavelet packet decomposition

由于ERD/ERS现象在想象左右手中体现为µ节律8～13 Hz 和β节律13～30 Hz能量的不同，本研究选用小波包分解的第四层的CD4、第五层的CD5进行信号的重构。经分解并重构后，很好的对脑电信号进行进一步降噪并使特定频段能量特征更加突出。降噪后信号，如图5所示。

2.3 分类

分类采用线性距离的阈值进行判定，不需要特别的设计分类器。

把脑电信号的每次试验开始后5～7 s的数据作为能量特征输入，判断C3通道和C4通道能量的大小，其能量差记作γi。

其中，Pc3(i)、Pc4(i)分别是C3、C4通道对比区间的能量。γi>0或γi<0意味着第i个试次是属于想象L类或R类。

2.4 衡量标准——Kappa系数

Kappa系数是由Cohen在1960年提出的，是一种衡量分类精度的方法，它使不同任务下的分类正确率标准转化成用统一参数即Kappa进行衡量，使得多分类任务性能的比较更加公平[20]。Kappa计算结果为-1～1，但通常Kappa是落在0～1间，可分为5组来表示不同级别的一致性：0.0～0.20为极低的一致性(slight)、0.21～0.40为一般的一致性(fair)、0.41～0.60为中等的一致性(moderate)、0.61～0.80为高度的一致性(substantial)和0.81～1为几乎完全一致(almost perfect)。即Kappa值越大，表示对不同任务的分类越接近实际情况。

图5 降噪后想象左右手(5～7)s 数据对比Fig.5 Denoised data comparison of (5～7)s about left/right hand class

Kappa系数的计算公式为：

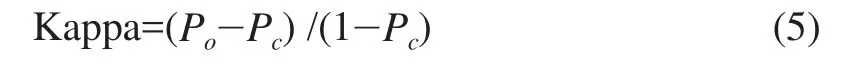
式中，Po为真实正确率，Pc为期望正确率。

设样本总数为n，真实为1类的样本数为a1，为2类的样本数为a0，预测为1类的样本数为b1，为2类的样本数为b0，真实label和预测label对应值相等的象元数为s，则

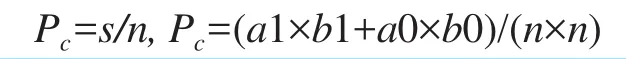
3 结论

本文的研究中，小波包分解采用Daubechies小波家族的db5作为基进行分解。

采用能量对比的方法，本文的特征提取和分类算法对BCI2008的竞赛数据BCICIV_2b_gdf，最优正确率93%，对各被试的两个试次的Kappa系数值如表2所示， Kappa系数的最优结果为0.6033，较竞赛结果略好。同时，由表2可得出，竞赛最优结果[21]对各个被试结果的样本方差为0.0763，本文所采用的方法得到的样本方差为0.0195，可见本文所采用的方法得到的处理结果更为平稳。

表2 本文试验结果与竞赛结果Kappa系数比较Tab.2 Results comparison of Kappa coefficients between this article and the competition

从以上的分析及结果可以看到，采用特定时间段能量对比的方法可以得到平稳且可靠度更高的结果，比较适合于在线系统，可以使繁琐的分类校准期和决策时间大大缩短；另外，也可以由此得出结论当人们看到提示想象或做单侧肢体运动后的2 s内，ERD/ERS现象最为显著[22]。同以往的方法[9-17,23]相比，该算法无疑既简单效果又好。但该算法是有不足之处存在的：该算法对于3种及以上的运动意识任务不能进行分类，因为多类的能量特征不能很好地使用能量差分离开，因此会对结果产生很大的偏差。但对于目前较为简单的两类意识任务的BCI接口，该方法还不失为一种简单可靠的方法，具有很大的应用空间。

[1]Birbaumer N,Heetderks WJ.Brain-computer interface technology：a review of the first international meeting[J].IEEE Trans Neur Syst Rehabil Eng,2000,(8): 164-173.

[2]Farwell LA,Donchin E.Talking off the top of your head: toward a mental prosthesis utilizing event related brain potentials[J].Electroenceph Clin Neurophysio,1988,70(1): 510- 523.

[3]Sutter EE.The brain response interface: communication through visually induced electrical brain response[J].J Microcomput App,1992,15(l): 31- 45.

[4]Pfurstcheller G,Lopes da Silva FH.Event-related EEG／MEG synchronization and desynchronizaiton: basic principles[J].Clin Neurophy,1999,110(11): 1842-1857.

[5]Wolpaw JR,McFarland DJ,Neat GW,et al.An EEG-based brain-computer interface for cursor control[J].Electroenceph Clin Neurophysiol,1991,78: 252-259.

[6]Kalcher J,Pfurtscheller G,Flotzinger D.Graz brain-computer interface: an EEG-based cursor control system[C].Proc IEEE EMBS,1993,1264-1265.

[7]McMillan GR,Calhoun GL,Middendorf MS,et al.Direct brain interface utilizing self regulation of steady state visual evoked response(ssver)[C].Proc 18th RESNA,1995: 693-695.

[8]付春梅.基于聚类分析法的脑电图数据分析的研究[D].大连交通大学,2007.

[9]李丽君.基于运动想象的脑电信号特征提取及分类算法研究[D].华南理工大学,2012.

[10]徐宝国,宋爱国.单次运动想象脑电的特征提取和分类[J].东南大学学报,2007,37(4): 629-633.

[11]吴婷,颜国正,杨帮华.一种快速的脑电信号特征提取与分类方法[J].系统仿真学报,2007,19(18): 4342-4344.

[12]裴晓梅,郑崇勋.基于Fisher判据时频分析的运动相关脑电特征选择及优化[J].西安交通大学学报,2008,42(8): 1026-1030.

[13]何庆华,吴宝明,彭承琳,等.基于小波和神经网络的视觉诱发电位识别方法[J].仪器仪表学报,2007,28(6): 1003-106.

[14]徐宝国,宋爱国,费树岷.在线脑机接口中脑电信号的特征提取与分类方法[J].电子学报,2011,5: 1025-1030.

[15]李丽君,黄思娟,吴效明,等.基于运动想象的脑电信号特征提取与分类[J].医疗卫生装备,2011,32(1): 16-25.

[16]王宏,赵海滨,刘冲.采用小波熵和频带能量提取脑电信号特征[J].吉林大学学报工学版,2011,41(3): 828-831.

[17]刘净瑜.运动想象脑电信号的识别方法及应用[D].北京工业大学,2009.

[18]李钟慎.基于MATLAB设计巴特沃斯低通滤波器[J].信息技术,2003,27(3): 49-52.

[19]徐长发,李国宽.实用小波方法[M].第二版,武汉: 华中科技大学出版社,2004.

[20]杨平,刘铁军,尧德中.支持向量机后验概率方法在多任务脑机接口中的应用[J].中国生物医学工程学报,2009,32(2): 171-176.

[21]竞赛最优结果[DB/OL].[2008].http://www.bbci.de/competition/iv/results/index.html#dataset2b.

[22]王江,徐桂芝,王磊,等.基于多通道自适应自回归模型脑-机接口系统特征的提取[J].中国组织工程研究与临床康复,2011,48(15): 9007-9010.

[23]金晶,王行愚,张秀.基于能量特征的左右手运动想象脑信号的识别方法 [J]. 华东理工大学学报,2007,33(4): 536-540.