水下航行器导航系统的模糊自适应多模型滤波方法

许昭霞，王泽元，吴振东

(1．中国人民解放军61081 部队，北京100094;2．中国人民解放军61618 部队，北京102102;3．中国船舶重工集团公司 第七一四研究所，北京100012)

0 引 言

高精度导航系统可保障水下航行器顺利完成任务，由于组合导航技术具有导航精度高，可靠性强等优点，被广泛应用于高精度导航系统［1］。对于组合导航系统模型为精确已知情况，可以用卡尔曼滤波方法进行状态估计，获得状态的精确估计值。但对于实际的水下航行器组合导航系统而言，因处于复杂的工作环境，不易获得精确量测噪声的统计特性，影响系统对状态误差的估计［2］。

为在线估计量测噪声统计特性，文献［3－4］采用自适应滤波方法，通过分析实时量测信息实际方差与理论方差的差异，设计推理模型在线实时调整量测噪声矩阵。文献［5］采用模糊系统调整滤波器的增益系数，在线自适应调整子滤波器，并对联邦滤波器信息分配系数进行模糊自适应调整。但是这些方法均假设系统模型固定不变，降低了估计算法的抗干扰能力。

本文针对上述问题，为提高估计精度和抗干扰特性，将模糊逻辑与多模滤波算法相结合，设计了基于模糊自适应的改进多模型滤波算法，减少模型误差对状态估计的影响，利用滤波信息的统计方差和计算方差的偏差作为模糊系统输入，设计模糊推理系统调节量测噪声方差。所提方法可以增强系统滤波模型对外部环境的适应性，有效提高水下航行器组合导航系统的精度。

1 组合导航系统滤波模型分析

对于水下组合导航系统，线性化后离散系统数学模型如下［5－6］:

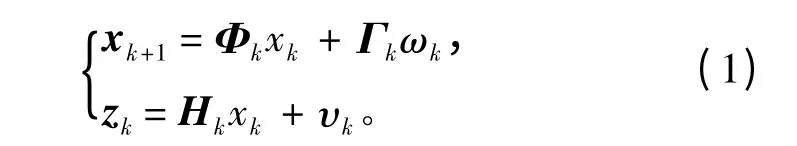
式中:xk为状态向量;zk为观测向量;Φk为状态转移矩阵;Γk为噪声干扰矩阵;Hk为观测矩阵;ωk，υk为零均值高斯白噪声，且。

由于水下航行器处于复杂的工作环境，当其滤波模型建模为式(1)的形式，对外部环境的适应性不强，因此建模为含有时变参数的卡尔曼滤波模型［7］，考虑到水下航行器滤波模型在状态方程中不包含时变参数，时变参数只影响观测方程，针对此特点，对多模型方法进行改进，建模为如下形式:

式中:sk为时变参数向量，其取值为有限的一系列真实值，sk∈{s1，s2，…sn}，n 为参数向量可能取值的个数，sk只影响系统观测方程，且其变化符合半马尔科夫假设，离散系统式(2)可以依据参数sk的不同分为n 个子系统。

基于贝叶斯估计理论和全概率公式，在估计方差最小条件下，sk的最优估计为:

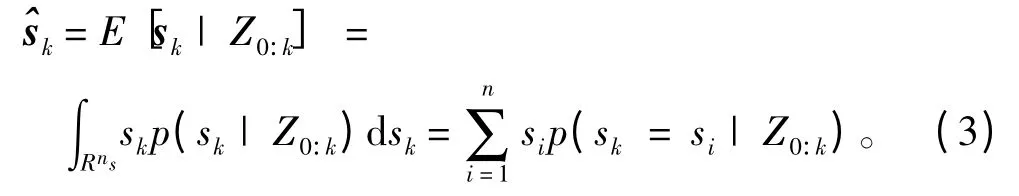
式中:模型匹配概率p(sk=si| Z0:k)计算公式如下:

式中:分母p(zk| Z0:k－1)为归一化系数，由全概率公式计算。式(4)中分子第一项似然函数p(zk|Z0:k－1，sk=si)与最新观测量zk有关，体现观测更新后的模型概率更新，利用子滤波器的观测信息γk(si)及其协方差阵Sk(si)求得，即

式中γk(si)和Sk(si)为观测新息及其协方差阵。

式(4)中分子第二项p(sk=si| Z0:k－1)体现先验知识，利用马尔科夫状态转移概率递推求得，即

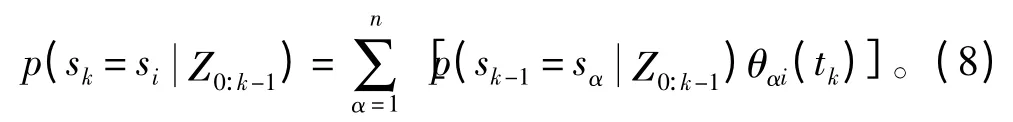
通过式(3)～式(5)和式(8)，可得到参数sk的估计值，将代入式(2)，消除滤波模型的不确定性，然后可采用扩展卡尔曼滤波算法得到状态的估计值。

2 模糊自适应多模型滤波算法

从上述分析可知，求解式(5)过程中需要得到准确的观测噪声统计特性，然而，在实际应用中，由于环境干扰等多方面因素，很难先验给出观测噪声方差的精确值，降低似然函数的估计精度，进而影响多模算法整体估计性能，下面给出本文提出的模糊自适应扩展卡尔曼滤波结构，应用协方差匹配技术设计模糊推理方法，在线调整传感器观测噪声协方差矩阵。

2.1 模糊自适应扩展卡尔曼滤波结构

观测信息的实际协方差通过在1 个大小为N 的移动估计窗口中取平均值近似得到:

式中:i0=k－N+1 是在估计窗中的第一次采样，这表明只有最后的N 个采样时刻的γi值被用于估计其协方差，N 根据经验选取使得协方差的计算具有较好的统计性(N=10 或15)。当信息序列的实际协方差与其理论值有偏差时，通过模糊推理系统根据这个偏差调整Rk。为了描述与Sk之间的偏差，定义新的变量匹配度:

理论上说，如果滤波过程中设定的Rk与真实值相符，则Mk应该为一小量，因此可以通过判断Mk的大小来自适应调整Rk的大小，进而改变Sk的大小，使Mk趋于0。由于Rk为对角阵，可以设计单输入单输出的自适应算法调整Rk的第i 行上的对角线元素Rk(i)。为了调节系统特性，设定相对于Rk(i)阀值μk(i)＞0，具体调节方式如下:

2)如果Mk(i)＞μk(i)，表明减小Rk(i)值。

3)如果Mk(i)＜－μk(i)，表明，增大Rk(i)值。

式中:ΔRk(i)为每个瞬时时刻从Rk(i)中增加或减去的因子;ΔRk(i)为模糊推理系统的输出;Mk(i)为模糊推理系统的输入。系统结构如图1所示。

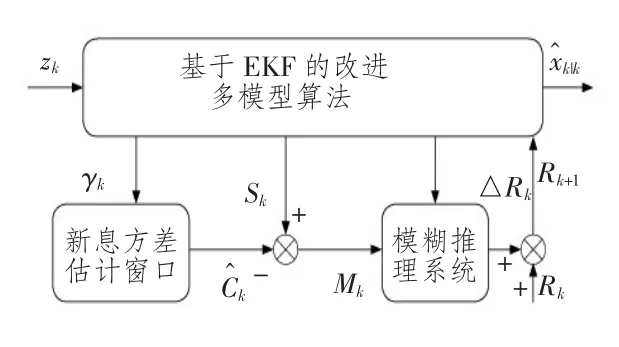
图1 观测噪声方差模糊自适应滤波结构图Fig.1 Block diagram of fuzzy adaptive filtering on measurement noise

2.2 观测噪声方差模糊自适应算法

由图1 可见，模糊推理系统的输入为新息序列的实际协方差与其理论值的匹配度Mk，输出为观测噪声估计值的增量。模糊推理系统的主要包括:数据预处理、隶属度函数定义、模糊规则和输出数据反模糊化。

1)数据预处理

为了实现算法的通用性，首先对Mk(i)进行归一化处理:

传感器的测量噪声调整量ΔRk(i)的范围定义与传感器特性当关，定义归一化的测量噪声增量。将的范围定义为［－1，1］，则测量噪声的增量由式(4)得到:

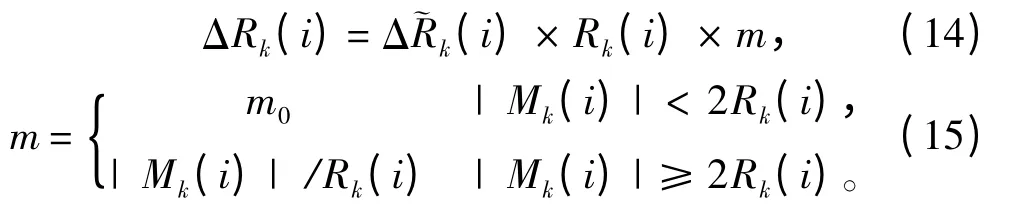
式中:m0为一正常数，m0的选取影响Rk(i)的收敛速度和收敛精度。m0值选取较大，Rk(i)可以迅速逼近真实的量测噪声矩阵，Rk(i)振荡严重;m0值选取较小，Rk(i)收敛速度较慢，估计方差较小。

2)隶属函数定义

模糊推理需要利用输入、输出变量的模糊集、论域和隶属度函数，将变量的精确值映射到模糊集上。定义的模糊集为P(正)，Z(0)，N(负)。~Mk(i)的隶属度函数采用三角形函数。输出变量是归一化的测量噪声增量，通过它实现测量噪声的自调节。定义的模糊集为I(增大)，M(保持)，D(减小)。输入输出变量的隶属度函数采用三角形函数，如图2和图3所示。

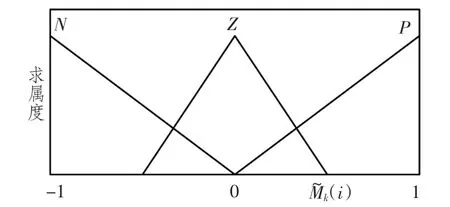
图2 观测噪声方差输入变量的隶属度函数Fig.2 Membership grade of measurement noise covariance input variable

图3 观测噪声方差输出变量的隶属度函数Fig.3 Membership grade of measurement noise covariance output variable

3)模糊规则

定义输入输出变量后，可以利用以下模糊规则进行模糊推理。每个模糊推理系统规则库中包括3个模糊规则:

4)输出数据反模糊化

2.3 算法实现

基于模糊自适应改进多模型滤波算法的计算步骤如下:

1)初始化

确定参数集合{s1，s2，…sn}和模型转换概率θαi(tk)，i=1，2，…n，α=1，2，…n，计算初始状态估计值、协方差阵。

3)更新模型概率

其中p(zk| ρk=ρi，Z0:k－1)由式(5)得到。

4)估算导引头观测方程阵

若k 小于设定观测窗口值设定值，则

若k 大于窗口值设定值，利用前面提出的模糊推理方法，得到ΔRk，则

利用式(4)和式(3)计算模型概率p(sk=si|Z0:k)，得到参数s 的估计结果。

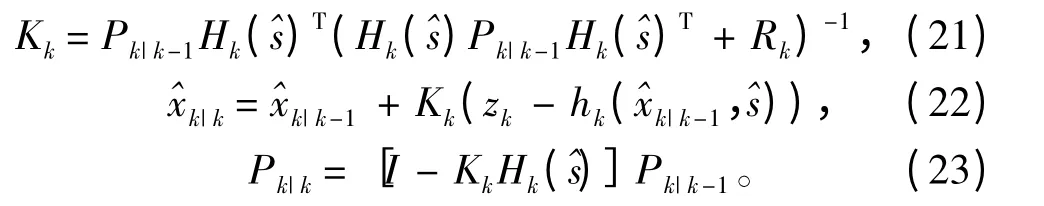
3 仿真结果与分析

仅考虑在固定水深下的航行，水下航行器组合导航系统的仿真模型和条件同文献［2］，仿真时间取1 000 s。从仿真时间600 s 开始，将系统噪声干扰的方差阵参数取为600 s 前的100 倍。

为验证本文提出方法的有效性，采用本文的方法和卡尔曼滤波算法进行仿真，2 种方法在纬度和经度方向的位置误差仿真结果如图4和图5所示。

由仿真曲线可知，采用模糊自适应改进多模型滤波算法可以有效地降低系统状态误差，加快滤波状态收敛速度;仿真时间在600 s 后，单一卡尔曼滤波器由于噪声矢量和方差阵固定不变，导致滤波效果不好，而模糊自适应改进多模型滤波算法仿真结果不受影响。

因此，在系统噪声和噪声模型不准确的情况下，模糊自适应改进多模型滤波算法可以有效地抑制系统滤波发散，提高系统估计精度。

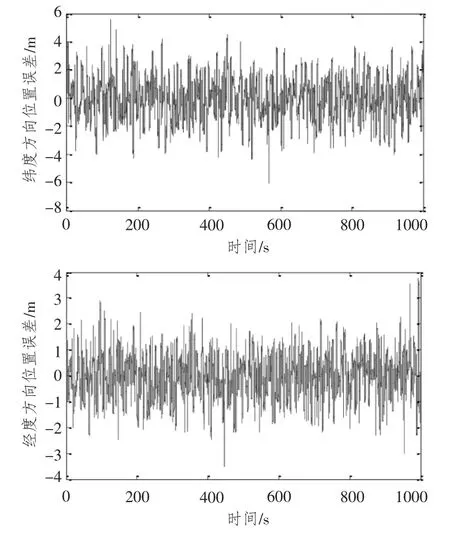
图4 模糊自适应多模型滤波算法的位置误差曲线Fig.4 Position error curve of fuzzy adaptive multiple model Kalman filtering algorithm

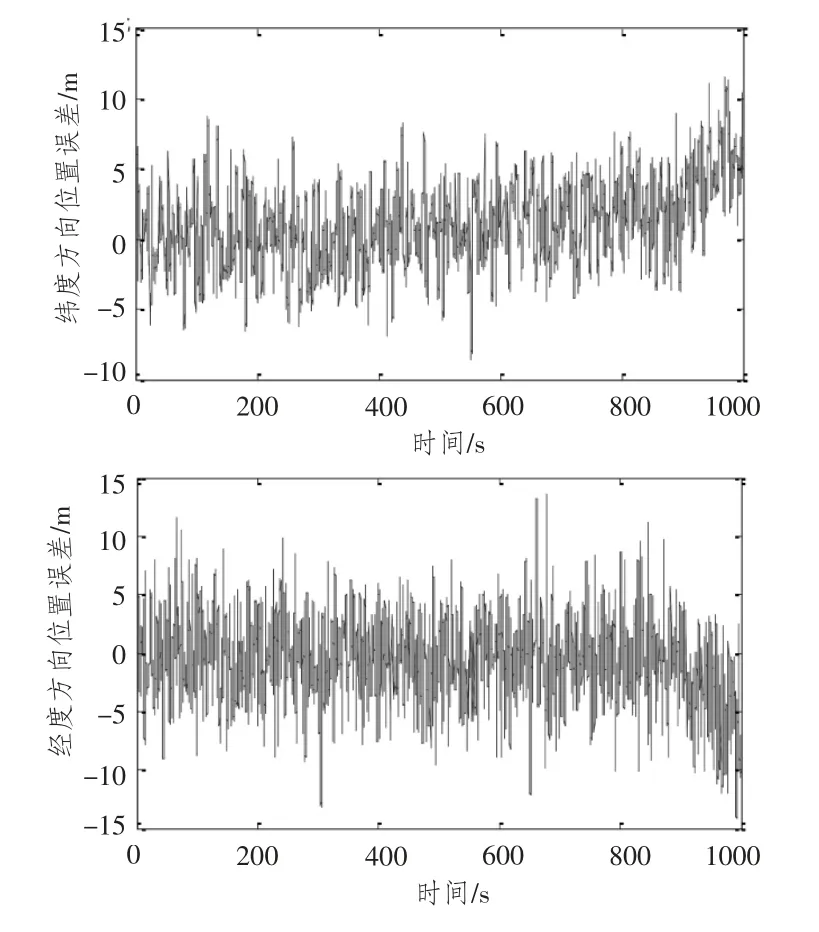
图5 卡尔曼滤波算法的位置误差曲线Fig.5 Position error curve of Kalman filtering algorithm

4 结 语

本文提出了一种基于模糊自适应改进多模型滤波的算法，可提高水下航行器组合导航系统的精度。针对观测噪声，设计采样窗口，在线统计滤波观测新息方差，然后应用协方差匹配技术设计模糊推理方法，在线调整传感器观测噪声协方差矩阵。仿真结果表明所提方法可增强估计算法的抗干扰能力，提高了估计精度。

［1］LI Kang-hua，WANG Jin-ling，LI Wan-li，et al．A noval INS and doppler sensors calibration method for long range underwater vehicle navigation［J］．Sensors，2013，13(14):583－600．

［2］HAO Yan-ling，MU Hong-wei．Application of integrated alignment in AUV based on GP－SRCDKF［J］．Advances in Information Sciences and Service Sciences，2012，4(21):598－605．

［3］LOEBIS D，SUTTON B，CHUDLEY J，et al．Adaptive tuning of a Kalman filter via fuzzy logic for an intelligent AUV navigation System［J］．Control Engineering Practice，2004，12(12):1531－1539．

［4］ZHU Feng-chun，JU Yan-bing，WANG Ai-hua．Research on integrated navigation technology of field robot［C］．2006 IEEE International Conference on Information Acquisition，2006:59－64．

［5］王其，徐晓苏，张涛，等．模糊自适应滤波在水下航行器组合导航系统中的应用［J］．中国惯性技术学报，2008，16(3):320－325．

［6］KIM H S，KIM I H．Design of adaptive fuzzy IMM algorithm for tracking the maneuvering target with time-varying measurement noise［J］．International Journal of Control，Automation，and Systems，2007，5(3):307－316．

［7］LI Wen-ling，JIA Ying-min．Consensus-based distributed multiple model UKF for jump markov nonlinear systems［J］．IEEE Transactions on Automatic Control，2012，57(1):230－236．