长期护理保险定价模型比较与分析
周海珍,杨馥忆
(浙江财经大学金融学院,浙江 杭州 310018)
一、引 言
我国目前已经进入老龄化社会,根据国家统计局的数据,至2013年末,我国60岁及以上人口占总人口的14.9%,其中65岁及以上人口则占了总人口的9.7%。在人类平均寿命不断延长的同时,各种老年性疾病如老年痴呆、中风截瘫、脑损伤等的发病率呈上涨趋势,再加之意外事故在老年人群中的高发生率,使生活不能自理的老年人所占的比重越来越高。
一直以来,我国老年人护理基本上沿袭的是居家养老方式,但“4-2-1”家庭模式和大量“空巢家庭”的出现改变正着传统的家庭养老观念和模式。另一方面,随着通货膨胀率和医疗费用的持续上涨,护理成本也呈逐年上涨趋势,导致了人们对医疗保险需求急剧增加。而我国现行的社会医疗保险制度尚不能提供长期护理保障,因此长期护理保险成为转嫁护理风险的有效手段之一,这同时也有助于我国健康保险体系的完善[1]。我国于2005年推出了商业长期护理保险,但至今市场上长期护理保险的品种并不多,且销量十分有限,这在一定程度上与长期护理保险在国内发展的时间比较短,经验数据匮乏,产品定价过程不规范和不完善有关。因此,选择合适的长期护理保险定价模型,对其进行深入系统的研究是非常必要的。
目前长期护理保险主要的定价方法包括曼联模型、减量表方法和马尔科夫模型。其中曼联模型(James.D.Craig,1930)是一种成熟且常用的模型[2];S.Haberman(1983)提及可运用减量表模型考察各健康状态的人数改变情况来计算状态转移概率[3];马尔科夫模型由于在模拟人群从健康状态向失能状态转移这一随机过程中具有数学上易处理和参数易估计的优点,在长期护理保险定价模型中被广泛应用。Beekman(1989)首次将长期护理过程视为一个持续的马尔科夫链,提出了计算长期护理保险保费的概率模型[4],Haberman(1997)扩展了Beekman模型,将马尔科夫过程的转移概率用一个明确的表达式加以阐述[5],Norberg(1995)提出了一种基于用以描述长期护理过程持续时间的马尔科夫链对长期护理产品定价的方法[6],在Haberman&Pitacco(1999)以准马尔科夫过程为基础建立了长期护理保险定价模型后[7],Levikson于2001年拓展了该方法,解决了个体在处于健康-失能循环下的定价问题[8],Robinson J.(2002)则利用连续时间的马尔科夫链模型对长期护理保险进行定价[9]。在国内,何林广(2007)分别运用上述三种方法模拟了长期护理保险的定价[10];陈岱婉(2008)运用多减因模型研究了在同时包括生存保障和死亡给付条件下的护理保险定价模型[11];李奇和张兆钺(2011)则对适合于中国长期护理保险产品定价的基础数据及相关问题进行了研究[12]。由以上分析可见,国外对长期护理保险定价模型的研究已经比较成熟,而国内对长期护理保险费率的研究相对较少,尚未形成一种适合我国的定价模型。本文将以美国常见的四种长期护理保险的定价模型为基础,将国内的实际数据代入以核算费率并进行比较,希望能从中选取一种适合我国目前实际需求和可得数据的定价模型。
二、长期护理保险定价模型
美国的商业长期护理保险发展较为完善,我们以美国长期护理保险的定价模型为分析基础,将这些模型大致分为不考虑状态转移的基础模型和考虑状态转移的动态模型两种类别。
(一)基础模型(不考虑康复的可能性)
基础模型只考虑被保险人从能够自理状态进入不能自理状态,并一直保持这种状态直到死亡,并不考虑被保险人从不能自理状态恢复到能够自理状态的情况。基础模型又可分为两种:第一种考虑了不能自理状态对后续年份的影响,用人均不能自理周数来定义不能自理的概率;第二种则将被保险人的一生划分为能够自理状态持续时间和不能自理状态持续时间两个随机时间段。
1.基础模型一:以人均不能自理周数表示不能自理概率
该模型基于全体人口的平均护理周数(护理率)来计算保费,假设只要被保险人进入不能自理状态,那么他将一直处于该状态直至去世。
如lx为年龄在x岁至x+1岁之间的生存人数,则不能自理概率sx等于某年龄段内所有人由于失能而需要的长期护理周数除以该年龄段内的总人数,如果一共不能自理r周,那么每个人的平均护理周数就为,即为不能自理概率。再假设对不能自理的人每周都给予1单位货币的给付,若赔付满足均匀分布,那么x岁至x+1岁之间所有人的给付折现到x岁时的现值是v1/2×1/2pxsx,其中v是折现因子;1/2px表示x岁的人存活半年的概率,通过岁时的人数除以x岁时的人数得到,根据均匀分布的假设,的人数就等于x岁至x+1岁之间的人数。模型假设x岁时产生的不能自理状态一直延续到去世,所产生的给付在x岁时的现值ASx为:
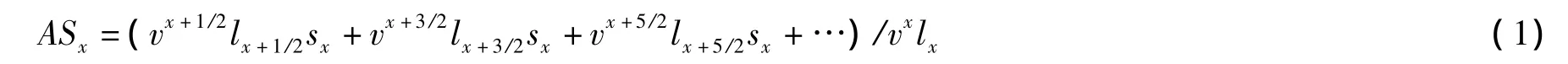
让Hx=vx+1/2lx+1/2sx+vx+3/2lx+3/2sx+vx+5/2lx+5/2sx+…,Dx=vxlx,则该模型下长期护理保险的趸缴纯费率ax为:
2.基础模型二:状态持续时间是随机变量
假设被保险人一旦陷入不能自理状态将持续至死亡,陷入不能自理状态和死亡都属于随机事件且相互独立,因此被保险人的一生将划分为两个随机时间段:能够自理状态持续时间和不能自理状态持续时间,这两个状态的持续时间都与被保险人的年龄有关。

以qax表示能够自理状态下的死亡率,qix表示不能自理状态下的死亡率,ix表示x岁时陷入不能自理状态的概率,aTix表示能够自理状态的持续时间,Tiy表示不能自理状态持续时间。若aTix=t1,则对应的概率等于从x岁到x+t1岁的过程中能够自理状态下的存活概率乘以x+t1岁时陷入不能自理状态的概率,即若Tiy=t2,对应的概率则是从y岁到y+t2岁的过程中不能自理状态下的存活概率乘以y+t2岁时不能自理状态下的死亡率,即Pr(Tiy=t2)
假设一位x岁的被保险人经过aTix=t1时间后,在y岁时由自理状态转移到不能自理状态,如果被保险人进入不能自理后每年都可以获得1个单位货币给付,那么未来全部的给付贴现到x岁时的现值为由于两个状态相互独立,因此他们的联合概率等于二者概率的乘积。因此该模型下长期护理保险的趸缴纯费率ax为:

(二)动态模型(考虑被保险人不能自理状态的转移)
事实上,在一定时间段内,个体的状态可能改变,而且处于某种状态的人数也会改变,因此在费率厘定时不光要考虑个体不能自理状态的发生,也要考虑不能自理状态的转移。动态模型也可分为两种:第一种是假设能够自理和不能自理状态交替反复出现直到个体去世;第二种则是个体在能自理、不能自理,死亡三类状态间转移。
1.动态模型一:Beekman模型
假设被保险人在某段时间内处于能够自理状态,随后持续一段时间不能自理,而后康复能够自理并保持一段时间,之后再次转移到不能自理状态,如此交替反复直到去世[3]。如图1所示,假设某人x岁,在x+t1岁时陷入不能自理状态,在x+t2岁时康复回到能够自理状态,在x+t3岁时再次恶化到不能自理状态,然后一直交替反复于能够自理与不能自理状态之间直到死亡。在实际应用中交替次数一般取3次或4次。

图1 Beekman模型时间轴
假设处于不能自理状态的被保险人每年均可得到1单位货币的给付,那么在第j次进入不能自理状态之后,在该阶段得到的所有给付在x岁的现值为:

由于j取值不定,所有关于时间的变量都是随机的,无法求出现值,因此需要引入新的变量简化模型。再者,陷入不能自理状态往往先于获得护理给付的时间,因此引入加权因子hx,表示x岁时陷入不能自理状态却未能获得给付的比例,而t1的含义则进一步细化为第一次获得护理给付的时间。在改进后的模型中用n(x,t1)表示处于不能自理状态且获得护理给付的年数,该变量与x岁时预期寿命ex和自理状态预期寿命(ae)x之差相关,即n(x,t1)=hx+t1·[ex+t1-(ae)x+t1],于是给付现值变为vt1(1-vn(x,t1))/(1-v),设jx(t1)表示t1的概率密度函数。在实际运用中,现值期望E(ASx)往往取五年为一个时间段进行计算,有:

其中k=0,1,…,最大取值与被保险人的投保年龄相关。购买长期护理保险的年龄大多为40或50岁,因此式(5)中c一般不大于10。该期望值近似等于:

即为长期护理保险纯费率ax。其中n(x,5k+2.5)=5hx+5k[ex+5k+2.5-(ae)x+5k+2.5]表示给付获得年数;密度函数表示第一次获得给付的时间t1在区间[5k,5k+5]范围内的概率,可由x岁的被保险人存活到x+5k岁的概率和x+5k岁至x+5k+5岁之间陷入不能自理状态概率相乘得到,但由于陷入不能自理状态和领取保险给付这两个事件可能并不同时发生,因此概率乘积还需要进行一定的调整,乘以加权因子5hx+5k,最后对k进行累加。
2.动态模型二:离散时间的马尔科夫链模型
假设被保险人存在能够自理(a)、不能自理(i)、死亡(d)三种状态,其中向死亡状态转移是单向的,不可逆转;能够自理状态和不能自理状态之间则可以相互转移,并且从x岁至(x+1)岁的状态转移满足离散时间的马尔科夫链,如表1所示。

表1 三状态模型转移概率矩阵
其中:
能够自理持续概率sax=健康人群存活率pax-不能自理发生率

康复概率rx=不能自理状态存活率pix-不能自理状态持续的概率
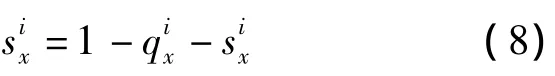
以aax,d表示x岁时处于能够自理状态的人一生所领取的所有给付,aix,d表示x岁时处于不能自理状态的人一生所领取的所有给付。x岁时处于能够自理状态的人在x+1岁时可能出现三种情况:仍然处于能够自理状态、进入不能自理状态、死亡,因此aax,d应该等于x+1岁时三种情况下领取给付加权平均后的现值,权重为各自发生的概率。其中x+1岁时仍然处于能够自理状态所领取的给付是aax,+d1,对应的概率为sax;x+1岁时进入不能自理状态所领取的给付是aix,+d1,对应的概率为ix;x+1岁时进入死亡状态之后将无法领取给付,因此给付为0。aix,d也可同理得到。假设被保险人在不能自理状态中每年可以获得1单位货币的护理给付,那么可得出如下的递推公式:

运用迭代法则,通过式(9)和式(10)即可以求得个体在x岁时能够自理和不能自理状态下的一生给付,再分别乘以两种状态的人数比例(不能自理的人数比例记为Kx)并加总则可得长期护理保险的趸缴纯费率ax:

(三)定价模型比较
基础模型一在构建思路和运算方面都较为传统,易于理解,可将各年龄的护理率进行统计,分析比较护理率随年龄变化的趋势,但它以人均不能自理的周数来定义不能自理发生概率并不十分准确,因为对于长期护理保险定价而言,更应关注的是被保险人每年新发生的不能自理的概率,即状态的转换率,而不是有多少人处于不能自理状态或自理状态持续多长时间;基础模型二则将生命划分为两个随机的时间段:能够自理状态和不能自理状态的持续时间,因为涉及两个随机变量,会让计算变得复杂,但却更加接近实际应用的需求。因此就两种基础模型而言,基础模型二可能更适合。
但长期护理保险定价的基础模型毕竟没有考虑被保险人状态的转移,即认为被保险人一旦进入不能自理状态,便保持这种状态直至去世,但在现实生活中并不一定如此,在上一年龄段进入不能自理状态的人在下一年龄段有可能继续维持不能自理状态,也可能会康复或去世;动态模型则考虑到了这一点,把康复的可能性加入模型,认为被保险人能不断地在能够自理状态和不能自理状态之间转移,直至最终进入死亡状态。因此相对于基础模型,动态模型更符合实际。
在两种动态模型中,Beekman模型考虑到被保险人进入不能自理状态和开始领取护理给付并不一定同时发生,因此对状态转移概率进行加权处理,而且该模型使用预期寿命和自理状态预期寿命的差值来度量领取给付的时间,这是它与其他模型迥异的一点,但是Beekman模型中存在积分,且以5年为一个时间段进行计算,求解的过程复杂且粗略,同时在实际应用中,目前我国并没有加权因子的统计数据,借用别国的数据会影响模型的适用性;而离散时间的马尔科夫链模型则考虑了各年龄段的康复概率,允许个体在不能自理状态和能够自理状态之间相互转移,更加符合实际,同时可以依据年龄和性别构建转移概率模型进行定价,使定价结果更公平合理,更具有现实意义。因此就两种动态模型而言,离散时间的马尔科夫模型可能更适合。
通过对上述四种定价模型的比较和分析,可以看出离散时间的马尔科夫链模型不失为一种较好的选择,可以将其作为我国长期护理保险定价模型的基础。虽然目前尚缺乏该模型中的康复率数据,但可以通过参考我国其他健康险以及医疗系统的相关统计数据近似得到。此外,随着医疗技术的提高,个体进入不能自理状态后的康复率会逐步提高,考虑了状态变化的马尔科夫链模型也会是一个较好的定价模型选择;且该模型可以通过细分不同护理状态扩展为多状态转移模型,有较强的灵活性和适用性。
四、马尔科夫链定价模型的数值核算
为了进一步验证离散时间的马尔科夫链模型作为我国长期护理保险定价模型的适用性和可行性,运用所能获得的我国实际数据,或经过简单运算后的数值代入模型进行核算。
(一)假设条件
1.投保年龄、保费缴纳及给付条件。假设一位60岁的男性以趸缴保费的方式购买一份长期护理保险,一旦被保险人陷入不能自理状态,保险人每年给予1单位货币的补偿直至被保险人康复或去世。同时,为简单起见,暂不考虑附加保费。
2.贴现率。本文不考虑利率风险和投资收益率,以银行一年定期存款利率3.25%作为不变的年贴现率。
3.不能自理人群的死亡率和长期护理状态发生率。我们利用式(12)来计算不能自理人群的死亡率。

其中,不能自理人群比例通过2010年人口普查数据获得,普通人群死亡率则采用《中国人寿保险业生命表(非养老金业务)2000-2003》数据。由于该生命表统计的是所有投保人群的平均死亡率,包括健康人群和次健康人群,而健康人群的死亡率应低于平均死亡率,因此,我们以生命表

其中,ix是X岁被保险人的不能自理发生率;qax是X岁健康人的死亡率;Kx是X岁人群中不能自理的比例;qix是X岁不能自理人群的死亡率。
(二)数值核算
假定被保险人在三个状态之间转移(死亡除外),被保险人获得给付的总现值ax=Kx×ai,dx+(1-Kx)×aa,dx中ai,dx和aa,dx可以通过迭代法求得,而每个年龄段的不能自理持续概率six,能够自理持续概率sax可由式(7)和(8)得到③由于篇幅关系,不能持续自理与能够持续概率具体数据不在文中列出。。其中不能自理人群的康复可能性很小且数据难以得到,因此我们假设康复概率为0。
假设个体预期最终寿命为100,因此aa,d100=0且ai,d100=1,可以迭代求得60岁时能够自理和不能自理状态下的一生给付:aa,d60=0.469302和ai,d60=3.273435,再分别乘以60岁时两种状态的人数比例累加后就可以得到总现值,为0.487904。
为了观察康复率对模型结果的影响,我们在上文的假设条件下,测算了康复率在不同水平时模型的核算结果。一般来说,随着年龄的增长,个体的康复概率逐渐下降,因此我们首先假设60-64岁的康复率为5%,65-69岁为2.5%,70-74岁为1.2%,75-79岁为0.5%,80岁以后康复率为0。在该假设下,计算可得投保人所需缴纳的纯保费为0.475511;若将60-79岁之间各年龄段的康复率增加50%,则纯保费为0.469865,减少了1.19%,敏感系数约为-2.37%。这说明在该模型中,康复率对核算结果有一定程度的影响,但影响不是很大。
从上述数值核算过程可见,利用现行可得的数据,可以运用离散型的马尔科夫链模型计算出一位60岁的男性购买长期护理保险时所需缴纳的纯保费,结果较为合理;并且,从康复率的敏感性分析可见,康复率对纯保费的影响并不大,因此在目前尚缺乏康复率统计数据的情况下,该模型也有一定的适用性。中平均死亡率的80%①[美]肯尼思·布莱克,哈罗德·斯基博著,孙祁祥、郑伟等译《人寿与健康保险》,经济科学出版社,2003年。估计健康人群的死亡率;然后借鉴李奇、张兆钺在《中国长期护理保险产品定价研究》中采用的公式(式(13))即可计算长期护理状态发生率②由于篇幅关系,生活不能自理人群死亡率与不能自理发生概率具体数据不在文中列出。。
五、结论与展望
通过对以上各模型的综述和比较,文章得到以下结论:第一,对于基础模型和动态模型而言,动态模型考虑了一生状态会不断变化这一事实,使定价更具有现实意义。第二,在两种动态模型中,离散时间的马尔科夫链模型在计算难度和数据可获得性方面都优于Beekman模型,同时,Beekman模型以五年为一个时间段进行计算,显得较为粗略。因此,在我国长期护理保险定价中,可以以离散时间的马尔科夫链模型作为定价的基础模型。
为进一步适应我国国情,可以对该模型做一些修正。首先,我国目前大部分长期护理保单选择单一的定额给付方式,容易因给付不足影响治疗或因给付过多而产生道德风险,根据被保险人在日常生活活动标准中不能完成的项目数及不能自理的项目内容来设计不同层次的护理给付则更为合理。因此,在定价时应引入多种护理状态,将离散马尔科夫模型中的不能自理状态细分为如不能洗澡、不能行走等多种状态,同时根据不能自理的项目数量和内容分别确定给付金额。其次,现实中可能存在不能自理状态和获得给付不同步的情况,可以考虑借鉴Beekman模型,引入加权因子进行调整。此外,对于目前尚缺乏的马尔科夫链中不同护理状态的转移概率及康复率数据,可以以医疗保险以及疾病保险的相关统计数据(这两个险种在国内开展的时间较长,数据相对完善)为基础并根据长期护理的特点进行加权调整;也可借鉴陈岱婉(2007)提出的根据转移概率、转移强度和护理时间之间的关系[13]来确定转移概率。
文章仅概述并比较了四种长期护理保险的定价模式,同时在数值核算中也做了诸多的简化处理,如未曾考虑利率波动和附加保费,将马尔科夫链模型中的康复率设为0等;此外,文章仅提出了离散时间的马尔科夫链模型可以作为我国长期护理保险定价的基础模型及一些模型的改进建议,但并未给出具体的修正模型,这都是在后续研究中可进一步探讨的问题。
[1]孙爱琳.论商业医疗保险与社会医疗保险的契合[J].商业经济与管理,2002,(11):48-51.
[2]James D.C..Actuarial basis for premiums and reserves in personal accident and health insurance [J].The Actuarial Basis for Premiums and Reserves,1930(17):51 -73.
[3]Haberman S..Decrement tables and the measurement of morbidity [J].Journal of the Institute of Actuaries,1983,(110):361 -381.
[4]Beekman J.A..An alternative premium calculation method for certain long-term care coverages [J].Actuarial Research Clearing House,1989,(2):39 -61.
[5]Haberman S.,Olivieri A.,Pitacco E..Multiple State Modelling and Long Term Care Insurance [M].Society of Actuaries,1997.
[6]Norberg R.Differential equations for higher order moments of present value in life insurance[J].Insurance:Mathematics and Economics,1995(17):171 -180.
[7]Haberman S.,Pitacco E..Actuarial Models for Disability Insurance [M].Chapman & Hall,London,UK,1999.
[8]Levikson B.,Mizrahi G..Pricing long term care insurance contracts[J].Insurance:Mathematics and Economics,1994,14(1):1 -18.
[9]Robinson J..A Long-term Care Status Transition Model[R].Unpublished paper,2002.
[10]何林广.长期护理保险定价研究[D].成都:西南财经大学硕士学位论文,2007.
[11]陈岱婉.综合责任长期护理保险的精算模型[J].山西师范大学学报(自然科学版),2008,(1):40-43.
[12]李奇,张兆钺.中国长期护理保险产品定价研究[N].中国保险报,2011-5-10(6).
[13]陈岱婉.长期护理保险精算模型的建立[J].重庆科技学院学报(自然科学版),2007,(12):136-138.

