三种分类预测模型在医学中的应用研究
(南方医科大学 公共卫生与热带医学学院 生物统计学系,广东 广州 510515)
在很多医学诊断和预后研究中都会用到统计预测模型,其中Logistic 回归是一种常被用于预测结果为二分类变量的统计方法.而神经网络作为一种新的技术,有学者(如曹志峰)认为它有可能代替Logistic 回归以及一些别的分类统计方法[1].BP (Back Propagation)神经网络是目前发展最成熟、应用最广泛的神经网络,是一种按误差逆传播算法训练的多层前馈网络.这一过程可以较迅速地通过调整网络中的权值以最小化网络输出和实际结果的误差.BP神经网络首先由Rumelhart,Hinton和Williams 提出,并逐渐在各领域被广泛应用[2].BP神经网络在医学领域中主要应用于疾病辅助诊断,如曹志峰将BP神经网络运用在甲状腺疾病的诊断上,结果显示网络对样本的判对率达到99.3%[1].而在BP神经网络中,由Mackay 提出的贝叶斯正则化的引入[3],是对传统BP神经网络的一种优化模型,可以修正BP神经网络中常出现的过拟合现象[4],从而提高其推广能力[5].国内研究对其应用还不够广泛,国外大多学者把这种神经网络用在工科领域[6-7],Yu 等人曾将此模型用于卵巢癌的诊断中[8].但总的来说,贝叶斯正则化BP神经网络在医学上的应用比较少,远不及其在工科领域的应用.因此,本文基于一个肾衰竭患者数据,应用BP神经网络、贝叶斯正则化BP神经网络与常用的二分类Logistic 回归对肾衰竭患者是否死亡进行预测,并比较三种模型的预测效果.
1 对象与方法
1.1 数据介绍及其来源
为了比较BP神经网络、贝叶斯正则化BP神经网络、Logistic 回归三者对同一个数据的预测效果,选用了《SPSS13.0 统计软件应用教程》上的一个关于急性肾衰竭(ARF)的数据[9].该数据为某医院1990~2000年中所有发生ARF的422名住院患者的临床资料.该资料共涉及29个变量,其中,器官衰竭和透析方式均为多分类变量,分别有5个水平和4个水平,已被重新分别设置4个哑变量和3个哑变量;计量资料有年龄、血肌酐、血红蛋白;其它均为二分类变量.把所有多分类变量转换成哑变量之后,该数据最后共涉及36个变量,见数据文件“ARF.sav”.
实际上,并不是自变量越多得到的模型效果越好,选择过多的变量往往会增加问题的复杂性,还会影响模型的拟合效果.本研究采用单因素Logistic 回归对自变量进行筛选,从中选取P值小于0.05的自变量,最终选取了24个自变量:age (年龄)、社会支持、慢性病、手术、糖尿病、肿瘤、cr (血清肌酐)、少尿、lbp(低血压)、黄疸、昏迷、辅助呼吸、心衰、肝衰、出血,呼衰、器官衰竭2个、器官衰竭3个、器官衰竭4个、dic (弥散性血管内凝血)、败血症、感染、透析方式1、透析方式3.
1.2 方法介绍
1.2.1 BP神经网络
典型的BP神经网络,是一个含有隐含层(既不属于输入层也不属于输出层,可同时存在多个隐含层)的三层网络结构,如图1所示.

图1 BP神经网络基本结构
BP神经网络训练主要分两个过程:输入变量的前向传播以及误差反向传播.全程流程图如图2所示.
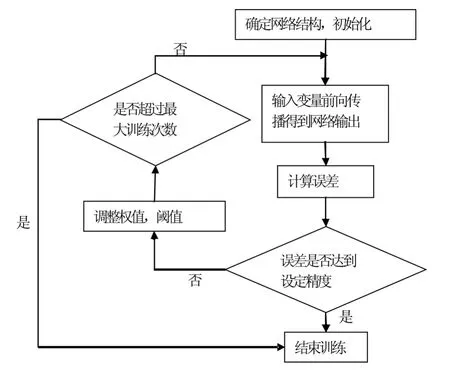
图2 BP神经网络训练流程
具体训练步骤如下:
(1)确定网络结构.
①确定隐含层层数.
1989年Robert Hecht-Nielson 已经证明对于任意闭区间内的一个连续函数,都可以用只含有一个隐含层的BP神经网络来逼近.本研究选用单个隐含层[10].
②确定隐含层节点数[11].
隐含层节点的选取,到目前还没有完善的理论依据,大多以经验为主,且有多种可参考原则,本研究用以下原则来确定隐含层节点数:m =log2n,其中,n为输入层节点数,m为隐含层节点数.本研究计算得出m约为4.55,四舍五入,以5为隐含层节点数.
③确定激活函数类型[12].
理论上已证明,至少一个S 型隐含层加上一个线性输出层的神经网络,能够逼近任何有理函数.因此,本研究隐含层激活函数f选用tansig 函数,输出层函数g选择purelin 函数.
(2)初始化[12].
根据样本输入、输出变量确定网络输入、输出层节点数n,其中,输入、输出层节点数可以不同,如当输入节点数为c,输出节点数为d时,神经网络就表达了从c个自变量到d个因变量的函数映射关系.初始化输入、隐含和输出层间的权值wij和wjk,隐含、输出层阈值aj和bk,其中i=k =1,2,…,n,j =1,2,…,m.(此处i=k是指输入层节点与输出层节点个数一致).学习速率设为0.01 (常用),最大训练次数设为20000,目标精度设为0.
(5)误差反向传播[2],根据梯度下降算法更新权值wij和wjk,阈值aj和bk.如:wjk(l+1)= wjk(l)+Δwjk= wjk(l)+ηδkHj、wij(l+1)= wij(l)+Δwij=wij(l)+ηδjxi、bk(l+1(= bk(l)+Δbk=bk(l)+ηδk、aj(l+1)=aj(l)+Δaj=aj(l)+ηδj.其中,η为学习速率,δk为输出层误差,δj为隐含层误差,l =1,2,…,M为训练次数.
1.2.2 贝叶斯正则化BP神经网络
实际上,贝叶斯正则化神经网络是在BP神经网络误差反向传播后增加一个贝叶斯正则化优化参数的过程.因此,对于贝叶斯正则化BP神经网络中BP神经网络那一部分的参数设置和计算等不再赘述,而贝叶斯正则化优化参数这一过程又分为正则化和贝叶斯推理两个部分,步骤如下[3,5,14]:
这里,我们记网络模型训练样本集D =(xi,yi),i=1,2,…,n,令网络框架为A(包括网络层数、每层节点数、激活函数类型),网络参数为w(包括三层间所有的权阈值),网络模型为O(x;w,A),误差函数为ED(D|w,为了缩减网络复杂度,给误差函数加一个权罚项1,2,…N.注意,这里提到的i和m在本节中分别表示样本数和网络参数(权值阈值)个数,不要与前面提及的记号混淆.由ED和Ew综合成一个新的目标函数(目标是指整个算法的最优化目标):M =αEw(w | A)+βED(D| w,A).其中,α,β为“黑箱子(black box)”参数[3],也叫超参数[14].实际应用时,最小化目标函数是为了减少网络训练误差的同时降低网络结构的复杂度.因为常规的正则化方法一般很难确定正则化参数的大小,而采用贝叶斯理论可以在网络训练过程中自适应地调节正则化参数大小并使参数达到最优,最后经过一系列推导,可以得到其中,γ=N-2αtr(M(wMP))-1,wMP表示M取最小值时所对应的网络参数值;γ表示有效的网络参数个数,反映网络的实际规模;N是网络中所有参数的个数.
1.3 软件实现及方法
用SPSS 21.0 对原数据中的变量进行筛选,以不同分界点作Logistic 回归并得出相应的判对率,画出三个模型的ROC 曲线并计算其AUC;用Matlab 训练BP神经网络和贝叶斯正则化BP神经网络并以不同分界点计算其判对率.
2 结果与讨论
2.1 不同分界点下三种模型判对率的比较

表1 不同分界点下三个模型的判对率
比较不同分界点下三个模型对同一数据的预测效果,观察分界点的选择对三个模型预测效果的影响,选择了0.3、0.4、0.5、0.6 与0.7 五个分界点,结果见表1.可见三个模型以0.5为分界点时判对率最高.此时,Logistic 回归模型的灵敏度为81.6%,特异度为93.4%;BP神经网络模型的灵敏度为84.6%,特异度为93.1%;贝叶斯正则化BP神经网络模型的灵敏度为96.3%,特异度为99.6%.
2.2 三个模型ROC 曲线及曲线下面积(AUC)比较
以三个模型输出的原始结果为基础画出三个模型的ROC 曲线(图3)并求出曲线下面积(表2).直接比较两个ROC 曲线下面积的95%可信区间是否交叉,如交叉,则表明两个ROC 曲线下面积在α =0.05时无显著差异;如不交叉,则有统计学差异[15].可见,BP神经网络和Logistic 回归比较,它们的AUC 无显著差别,而贝叶斯正则化BP神经网络和上述二者比较,它们的AUC 有显著差别,且贝叶斯正则化BP神经网络AUC为三者中最大者,即模型预测效果最好.

图3 三个模型ROC 曲线图

表2 三个模型AUC 及95%置信区间
3 结论
针对本研究的数据,当三个模型的输出结果都以0.5作为分界点时,它们的判对率分别为89.1%(Logistic 回归)、90.05% (BP神经网络)和98.58%(贝叶斯正则化BP神经网络).用三个模型原始输出结果和目标数据作比较画出的ROC 曲线及求得的AUC分别为0.950、0.947和0.995.可见,针对这一数据,BP神经网络的预测效果并不像大多数以往研究中所说的会比Logistic 回归结果好[1,16-17],反而是和Logistic回归得出的结果差不多,但是贝叶斯正则化BP神经网络的预测效果比上述两个模型好很多.当然,不排除是由于数据样本量不足导致BP神经网络不能得到很好的训练,从而预测效果不如理想中准确.不过,本研究突出了贝叶斯正则化BP神经网络不需要大量的训练样本也能得到很好的输出结果这一优点.
[1]曹志峰.BP神经网络在临床诊断中的应用与探讨[J].实用医技杂志,2005,12 (9):2656-2657.
[2]Rumelhart D E,Hinton G E,Williams R J.Learning representations by back-propagating errors[J].Nature,1986,323 (9):533-536.
[3]MacKay D J C.A practical Bayesian framework for backpropagation networks[J].Neural computation,1992,4 (3):448-472.
[4]Moody J,Hanson S J,Lippmann R P.The Effective Number of Parameters:An Analysis of Generalization and Regularization in Nonlinear Learning Systems[J].Advances in neural information processing systems,1992,4:847-854.
[5]魏东,张明廉,蒋志坚,等.基于贝叶斯方法的神经网络非线性模型辨识[J].计算工程与应用,2005,41(11):5-8.
[6]Auld T,Moore A W,Gull S F.Bayesian neural networks for internet traffic classification[J].Neural Networks,IEEE Transactions on,2007,18 (1):223-239.
[7]Goh A T C,Kulhawy F H,Chua C G.Bayesian neural network analysis of undrained side resistance of drilled shafts[J].Journal of Geotechnical and Geoenvironmental Engineering,2005,131 (1):84-93.
[8]Yu J,Chen X W.Bayesian neural network approaches to ovarian cancer identification from high-resolution mass spectrometry data[J].Bioinformatics,2005,21 (1):i487-i494.
[9]陈平雁.SPSS 13.0 统计软件应用教程[M].北京:人民卫生出版社,2005,196-197.
[10]Hecht-Nielsen R.Theory of the backpropagation neural network[J].International Joint Conference on IEEE,1989:593-605.
[11]MATLAB 中文论坛编著.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社,2010,9-10.
[12]闻新,周露.MATLAB神经网络应用设计[M].北京:科学出版社,2000:225-232.
[13]MacKay D J C.Bayesian interpolation[J].Neural computation,1992,4 (3):415-447.
[14]李鹏.基于贝叶斯理论的神经网络算法研究[J].光机电信息,2011,28 (1):28-32.
[15]DeLong E R,DeLong D M,Clarke-Pearson D L.Comparing the areas under two or more correlated receiver operating characteristic curves:a nonparametric approach[J].Biometrics,1988:837-845.
[16]黄德生,周宝森,刘延龄等.BP人工神经网络用于肺鳞癌预后预测[J].中国卫生统计,2000,17 (6):337-340.
[17]Peng SY,Peng SK.Predicting adverse outcomes of cardiac surgery with the application of artificial neural networks[J].Anaesthesia,2008,63 (7):705-713.

