并行计算中组合空间问题的均衡划分研究
孙发军,彭际群
(怀化学院1.数学系;2.高性能并行计算中心,湖南 怀化 418008)
1 组合空间的划分问题
近年来,随着云计算的兴起,其基础技术——并行计算更是得到国内外广泛的研究[1-6].实际应用中通常有这样一类问题:需要从一个组合空间中通过穷举搜索寻求最优解或在组合空间上完成一定的计算,如交巡警平台的增设问题就是这样一例.
为了更有效地贯彻实施巡警服务职能,需要在市区的一些交通要道和重要部位设置交巡警服务平台.每个交巡警服务平台的职能和警力配备基本相同.假设该城市有92个路口,现已经设置20个巡警平台,根据现有交巡警服务平台的工作量不均衡和有些地方出警时间过长的实际情况,拟在该区内再增加2-5个平台,即在72个路口中选择其中2-5个,使得在平台个数增加尽可能少的情况下整个城市巡警工作量足够低且分配平均.
定义1组合空间的划分问题:并行计算中,给定k个cpu节点,如何把Cnm个组合动态均衡而又连续地分配给各cpu节点去计算的问题.
假设解决该问题的划分方案需满足以下要求:
(1)动态性:为了提高速度及满足一般性需要,我们假设这Cnm个组合是运行时动态生成和分配的.
(2)连续性:为便于各CPU 节点上的并行程序在自己连续的子空间内使用循环完成计算,如穷举搜索最优解,这就要求划分组合空间后的子空间应该连续;
(3)均衡性:划分后所得每一个子空间所含的组合数近似相等,最好能达到完全相等.
为了讨论该问题的解决方案是否均衡,我们定义了如下两个指标[2-4]:均衡指数和加速比.均衡指数用于理论分析中衡量均衡性,而加速比用于通过实验分析均衡性,因为通常来说均衡性越高所得到的加速比应该越大,而高加速比正是我们让划分达到均衡的最终目的.
定义2 均衡指数δ:设分配给n个CPU 节点的任务量分别为q1,q2,…,qn,则我们定义均衡指数为他们之间的标准差:
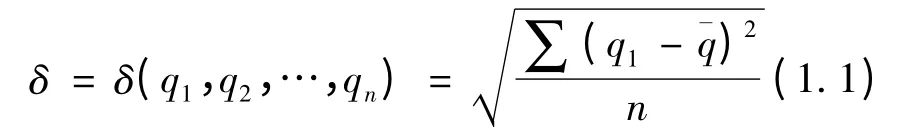
定义3 加速比η:算法串行计算时间ts和算法并行计算时间tp之比,即:

2 均衡划分研究
以前面描述的交巡警服务平台增设问题为例,记的组合为(u,v,w,x,y),(假设已设置的平台号为0~19,则其中20u87,21v88,22w89,23x90,24y91),现考虑将该组合空间划分成16个子空间,以方便将任务分配给16个cpu核并行执行,我们总结出下面的两类三种方案.
2.1 常规划分
考虑20u87,计u =20 时的组合为(20,v,w,x,y),计u =21 时的组合为(21,v,w,x,y)… 计u=87 时的组合为(87,v,w,x,y),这样就把C572的组合空间分成了68个u类组合.要将其划分成16个子空间分配到16个CPU 节点上则可为每个节点分配4-5 (由68 ÷16 =4.25)个u类组合,我们可得到划分并计算出了每个节点分配到的实际组合数如表1所示(为便于描述,文中所有节点号是CPU 节点号,一般来说一个CPU 节点是一个CPU 核).
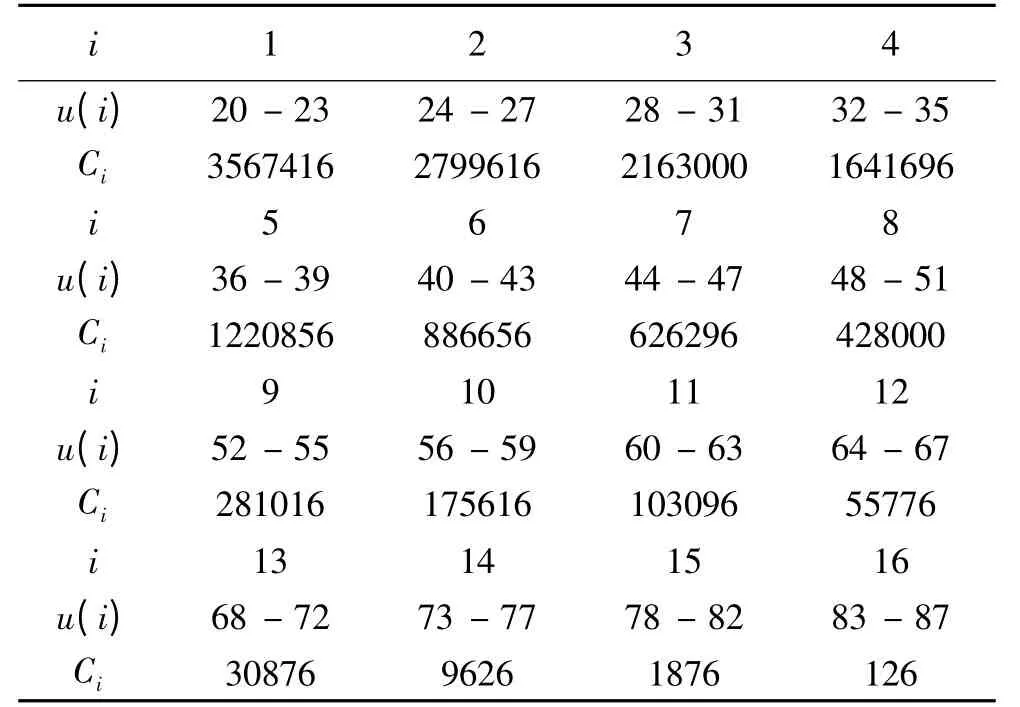
表1 u-均匀划分方案
记该方案为方案一,其均衡指数为标准差δ1=δ(C1/1000,C2/1000…C16/1000),计算得到δ1≈1080.5,均衡指数非常大表明各CPU 节点负载非常不均衡,最大值达到3567416个组合.
分析C37的分配情况我们不难发现产生以上现象的原因.C37的组合空间为(1,2,3),(1,2,4),(1,2,5),(1,2,6),(1,2,7),(1,3,4),(1,3,5),(1,3,6),(1,3,7),(1,4,5),(1,4,6),(1,4,7),(1,5,6),(1,5,7),(1,6,7),(2,3,4),(2,3,5),(2,3,6),(2,3,7),(3,4,5),(3,4,6),(3,4,7),(4,5,6),(4,5,7),(4,6,7),(5,6,7).对于C37的组合(u,v,w),若以均匀u为依据划分,很显然u =1 时的组合数是最多的,u值越大,其组合数越少,当u =5只有一个组合(5,6,7).
2.2 均衡划分
常规划分方案虽然实现了并行计算,提高了计算的速度,但因为出现了明显的负载不均衡现象,没有充分发掘出任务的并行性.由表1可以总结出,不能以u为标准去划分整个组合空间,因为对于不同的u,其组合(u,v,w,x,y)的个数本身就是不均衡的.
分析u,v,w,x,y组合的分布规律我们发现,w的组合分布相对更均匀(如表2所示),表2为不同的k值的组合(u,v,w,x,y)的个数.
于是我们考虑以w(22w89)为标准进行划分,这样我们可给每个节点平均分配4-5个w值得到如表3所示的w-均匀划分方案(记该方案为方案二),然后可据式(1.1)计算出均衡指数为δ2=462.77,最大值降为1487196个组合,不到常规方案的42%,可见方案二比方案一的均衡性好很多,计算时间理论上可缩小一半以上.
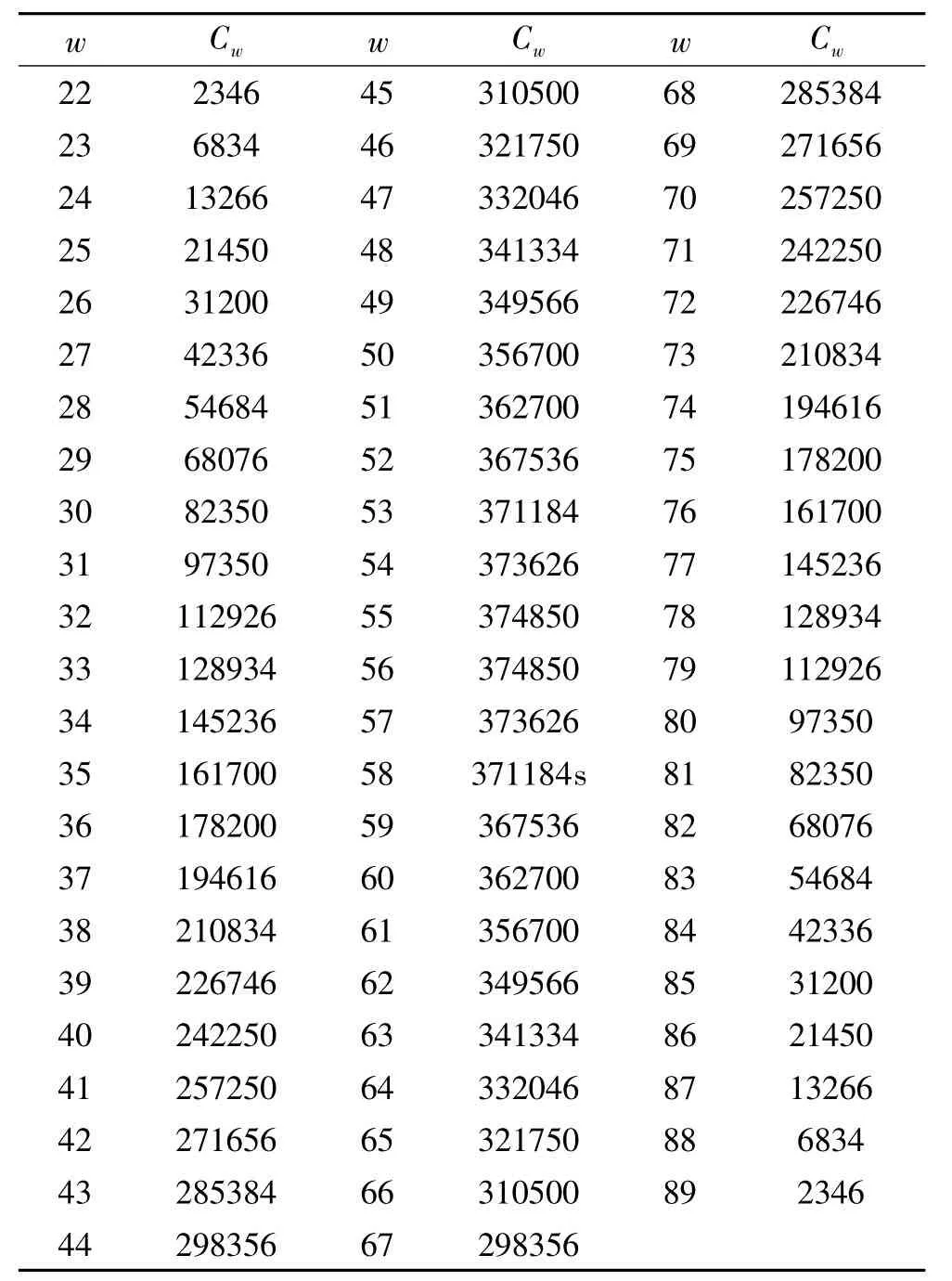
表2 不同w值的组合个数
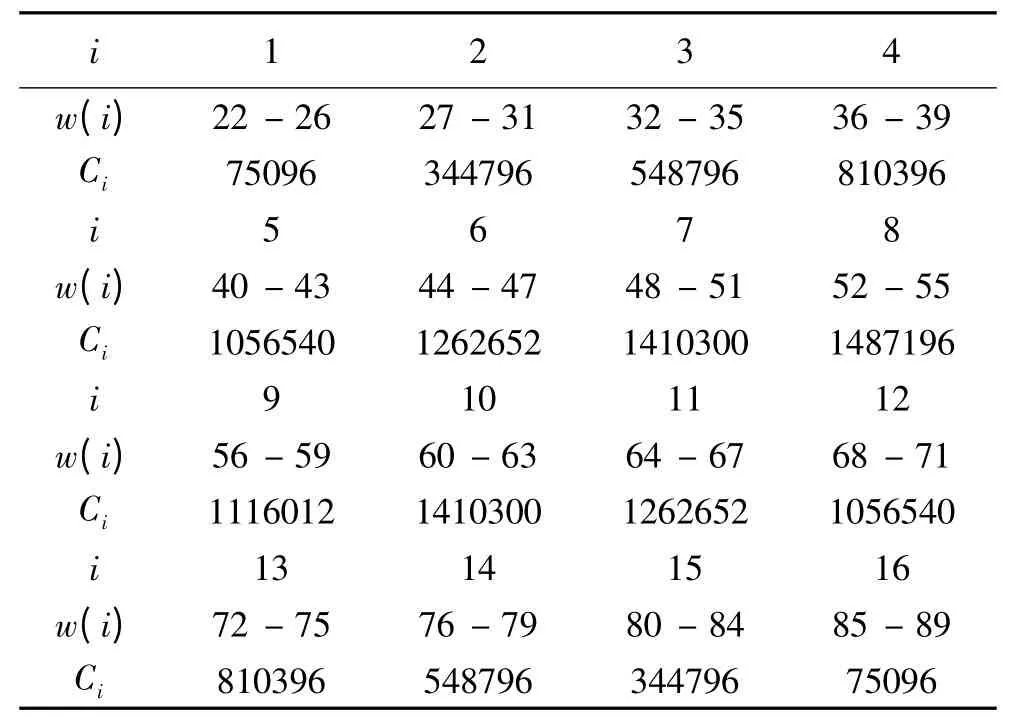
表3 w- 均匀划分方案
事实上,为使各节点负载更均衡,我们可不均匀分配w值来进行划分,而是先统计出每一个w的组合(u,v,w,x,y)的个数(如表2所示),再根据组合个数进行子空间划分,且对于w=j的组合数与w =111-j的组合数相等.C572=13991544,13991544 ÷16 =874471.5,我们考虑为每个CPU 节点分配800000~900000个组合数,得到如表4所示的分配方案(记为方案三).
由式(1.1)可计算出方案三的均衡指数为,计算δ3=118.24,而最大组合数为1068966,对比方案一下的均衡指数δ1=2.335δ2=9.138δ3,显然δ3比δ1几乎小一数量级,从而可知均衡划分方案下各个CPU 节点负载更为均衡.
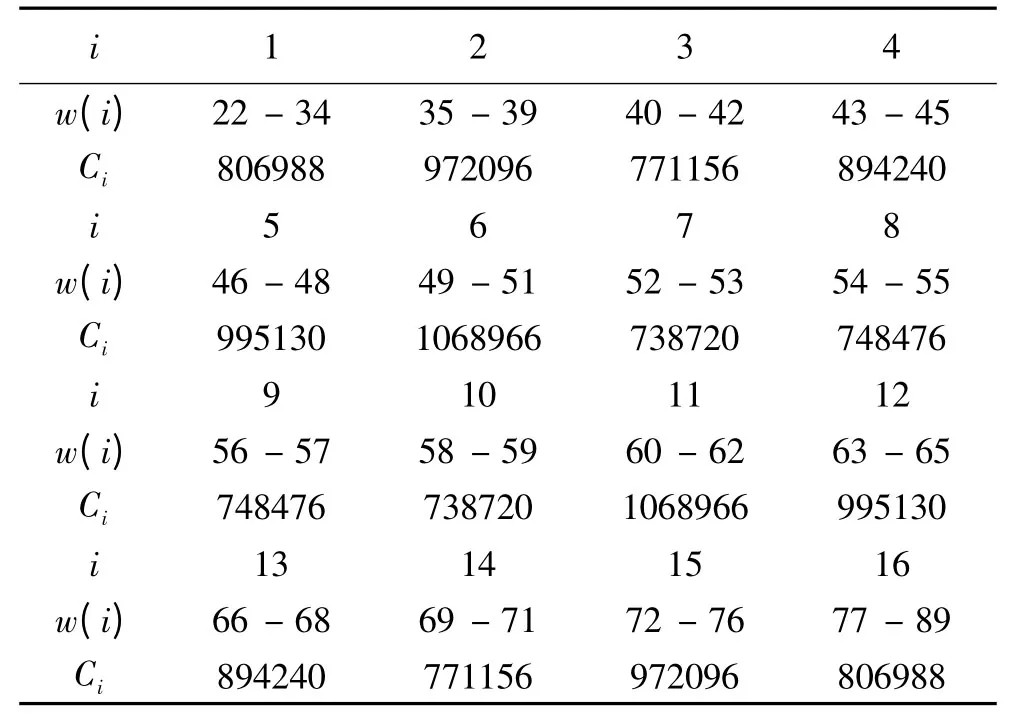
表4 w- 不均匀但更均衡划分方案
3 均衡划分的实验分析
为了便于比较各方案的优劣,我们定义并行计算的加速比为式(1.2)所示.
按这种方案划分,进行并行计算,发现经过30020.23 s 后计算完毕,速度明显比单节点串行快(串行所需计算时间为117554.85 s),我们可据式3.1 计算出其加速比为:

我们在曙光3600 系列服务器集群(10个2 路刀片服务器)上选择了16个cpu 核对以上三种方案进行了实验并记录了相应结果.
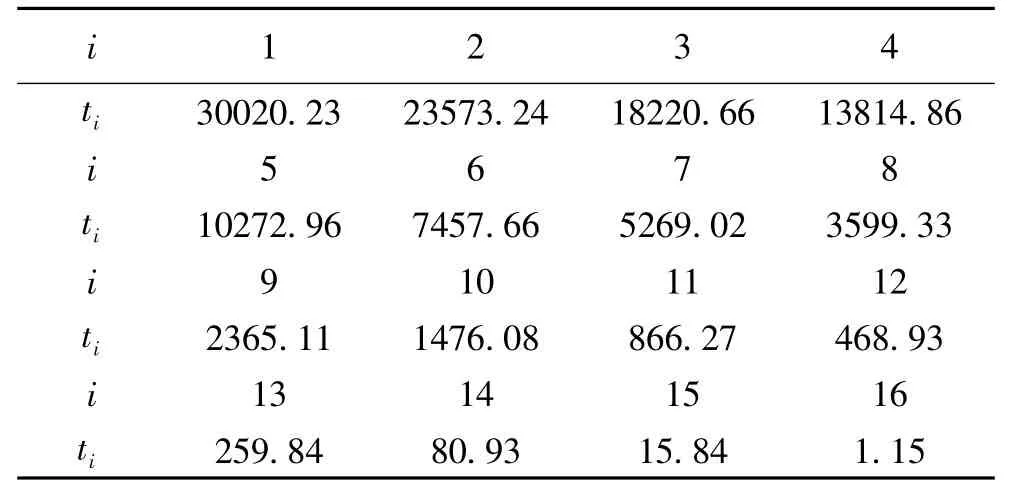
表5 u- 均匀划分的实验结果(单位:秒)

图1 方案一下16个节点的利用率
实验中我们记录的各CPU 上的计算时间如表5所示,记常规方案下第i号CPU 节点的利用率为ei,ei=ti/MAX(t1,…,t16)×100%,得到各个CPU 节点的利用率如图1所示.从图1中可以看出,CPU利用率差异很大,该方案下CPU 资源浪费严重.
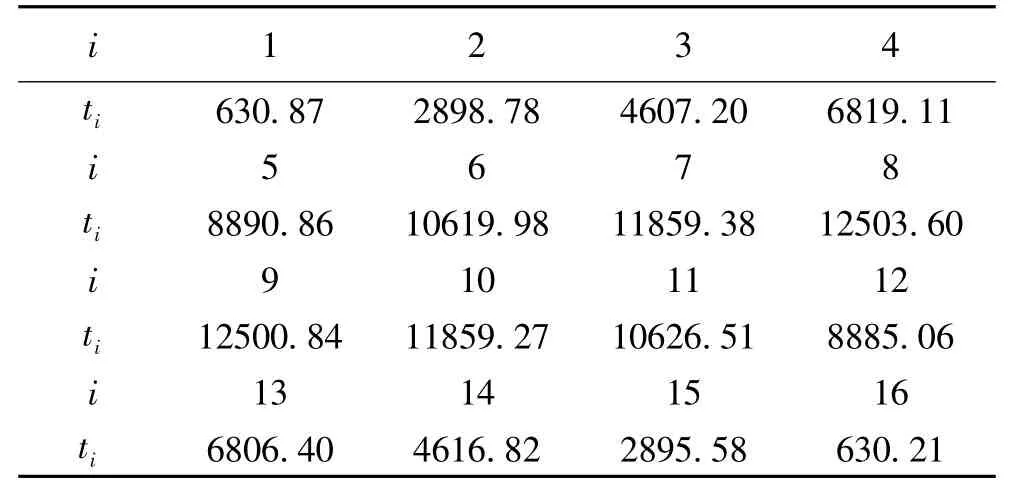
表6 w- 均匀划分的实验结果(单位:秒)
我们也记录了方案二的各CPU 计算时间如表6所示,依式(1.2)我们可计算出加速比为:
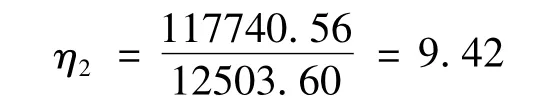
结果表明w-均匀划分相对于u-均匀划分提高了2.40倍.
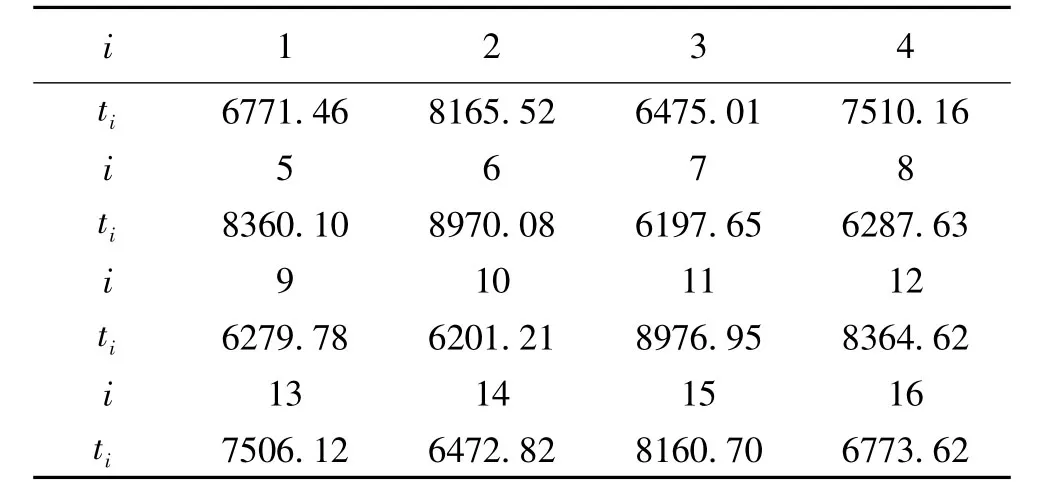
表7 w- 不均匀划分的实验结果(单位:秒)
而按方案三进行计算,各CPU的运行时间和利用率分别如表7所示,并可计算出各CPU 节点利用率如图2所示.
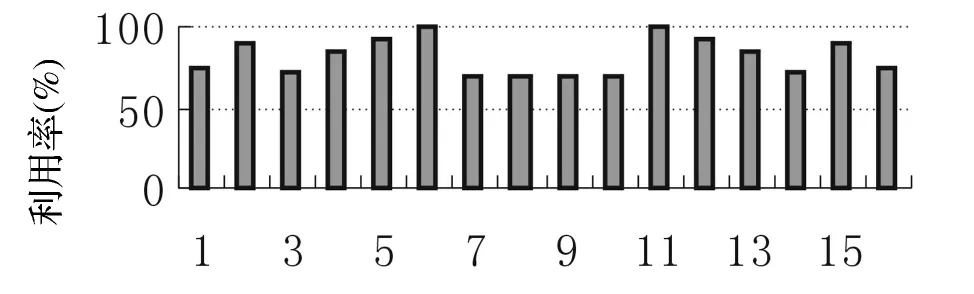
图2 方案二下16个CPU 节点的利用率
由图3.4可以看出,16个CPU 节点的利用率均比较高,CPU 资源得到了充分的利用.
同样我们可计算出加速比为:
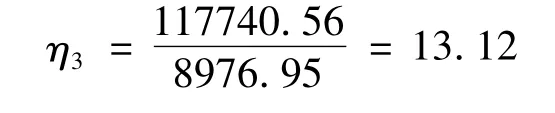
该加速比是u-均匀划分的3.35倍,是w-均匀划分的1.39倍,与理想值16 仅差2.88.
4 结论
论文提出的组合空间划分方案充分考虑了CPU负载均衡和各CPU的利用率,进一步挖掘了对称多处理机上并行计算的效率,但为了方便计算机的执行,组合空间采用了连续分配,导致各个划分子空间大小仍有差距,在图2中也可以看出,CPU 利用率最低约为63%,依然存在CPU 资源的浪费,在并行计算过程中会出现一定的负载不均衡现象,探索出方便计算机执行的非连续分配方案,进一步挖掘CPU 资源的利用率,将是后续研究的一个重要内容.事实上若将组合事先均等划分地存到文件中,然后将文件分派到每个节点上执行.这或许是种效率更高的方案,但从文件中读数据或许会增大程序的执行时间,从而也降低了计算速度,具体还有待进一步研究.
[1]汤继飞,李思,张理论,等.面向并行负载平衡的数据剖分技术[J].计算机应用研究,2010,27 (11):4015-4019.
[2]王之元,杨学军.并行计算系统度量指标综述[J].计算机工程与科学,2010,32 (10):44-48.
[3]郑秋亚,刘三阳,左大海,等.多块结构化网格CFD并行计算和负载平衡研究[J].工程数学学报,2010,27 (2):219-224.
[4]陈国良.并行算法研究方法学[J].计算机学报,2008,31 (9):1494-1502.
[5]马永刚,谭国真,杨际祥,等.一种改进的并行计算图划分模型[J].小型微型计算机系统,2011,32 (3):417-418.
[6]MENON S.Effective reformulations for task allocation in distributed systems with a large number of communicating tasks[J].IEEE Transactions on Knowledge and Data Engineering,2005,14 (12):1497-1508.
[7]Bokhari S H.Assignment problems in parallel and distributed computing[M].Norwell,MA,USA:Kluwer Acadermic Publishers,1987.

