分数阶系统的状态反馈控制

方园，王先超，马玉田 （阜阳师范学院数学与金融学院，安徽 阜阳236037）

分数阶微积分自被提出以来便被学者们广泛用于描述各类系统，分数阶系统的稳定性问题也越来越受到学者们的广泛关注［1－4］。下面，笔者主要针对带Riemann－Liouville导数的分数阶系统，讨论了状态反馈控制问题。

1 预备知识及问题描述

定义1 若α（n－1＜α＜n），函数ft（）的Riemann－Liouvill导数定义如下：

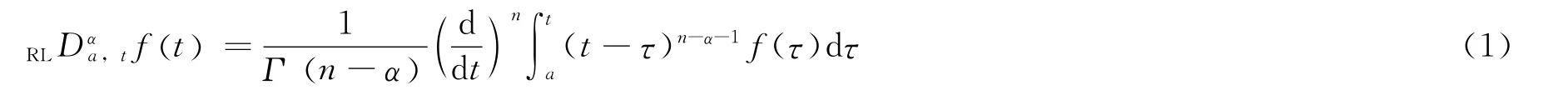
考虑带Riemann－Liouvill导数的线性分数阶系统：

定理1［3］若矩阵A中所有特征值满足则系统所有零解是渐近稳定的。

引理1［4］分数阶系统（2）渐近稳定的条件是当且仅当存在2个实对称矩阵Pk1∈Rn×n（k＝1，2）和2个反对称矩阵Pk2∈Rn×n（k＝1，2），使得：

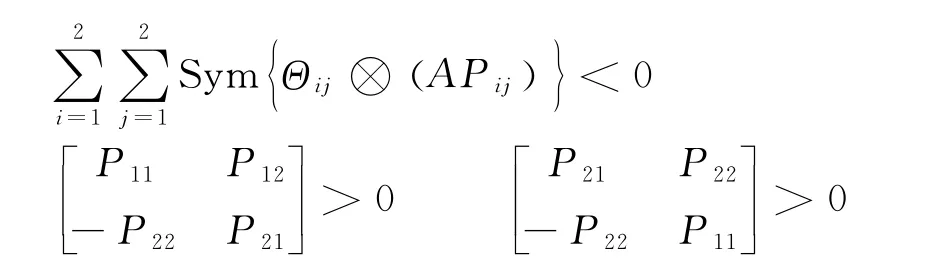
引理2［5］若系统（2）中矩阵A∈Rn×n，且1≤α＜2，则成立当且仅当存在对称矩阵P＞0使得：

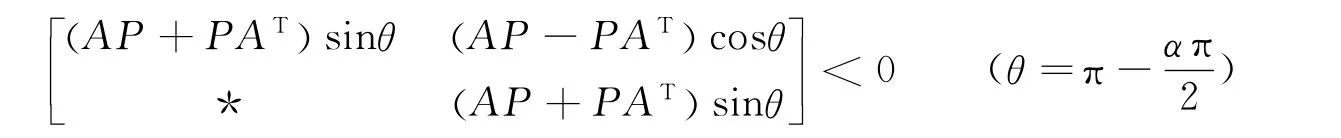
引理3［6］假设X、Y为适当维数的矩阵，则成立不等式：

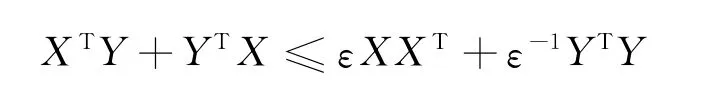
2 主要结果

考虑带R－L导数的分数阶系统：

式中，x（t）∈Rn为系统状态；u（t）是系统的输入；常数矩阵A∈Rn×n，B∈Rn×m，且矩阵A不满足为初始状态。

考虑反馈控制器u（t）＝Kx（t），带入系统（3）中可得：

2.1 0＜α＜1

定理2 若存在正定矩阵P11，P21，常数矩阵K，实数εi＞0（i＝1，2），使得矩阵：

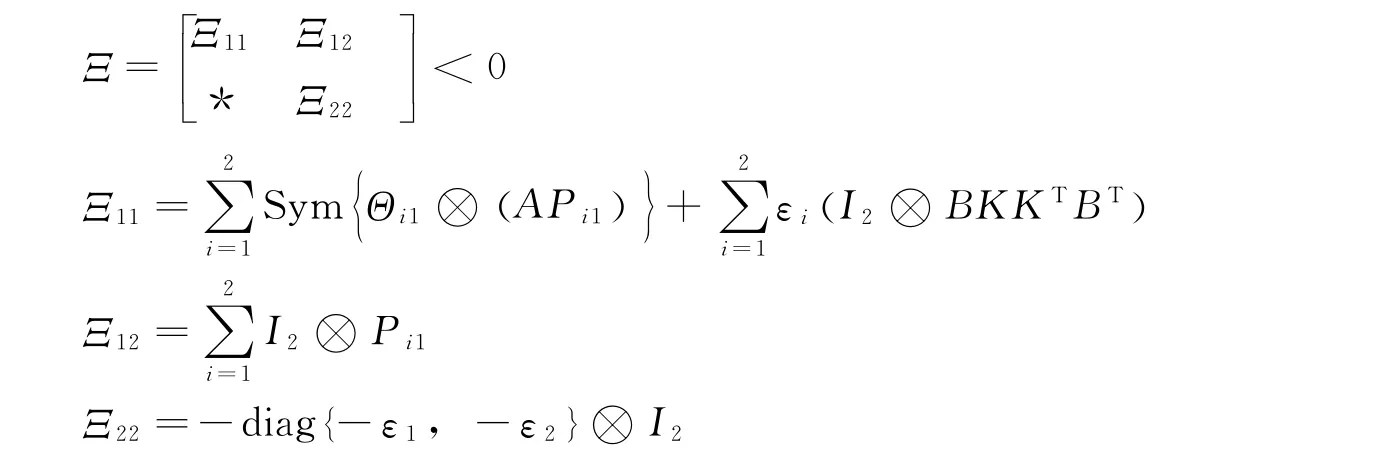
则带R－L导数的分数阶系统（4）是渐近稳定的。

证明 利用引理1可知，存在2个正定矩阵Pk1∈Rn×n，k＝1，2。 反对称矩阵Pk2∈Rn×n，k＝1，2。使得假设P12＝P22＝0，此时可以得出当满足条件时，系统（4）是渐近稳定的。其中不等式Φ＜0等价于：

记Θi1Θi1＝I，并利用引理3可知：对于任意实数εi＞0（i＝1，2），有：

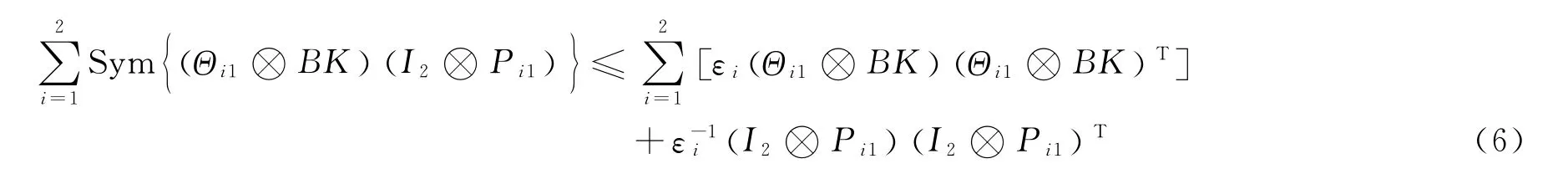
再利用矩阵Kronecker product性质，有：

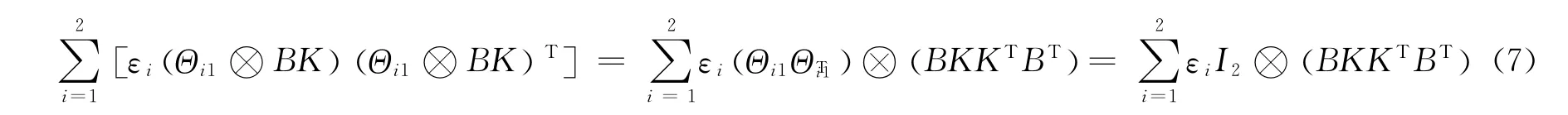
最后由矩阵的Schur补性质，式（5）、（6）、（7）等价于Ξ＜0。

2.2 1≤α＜2

定理3 存在正定矩阵P，常数矩阵K 和常量ε＞0，使得（线性矩阵不等式（LMI））：

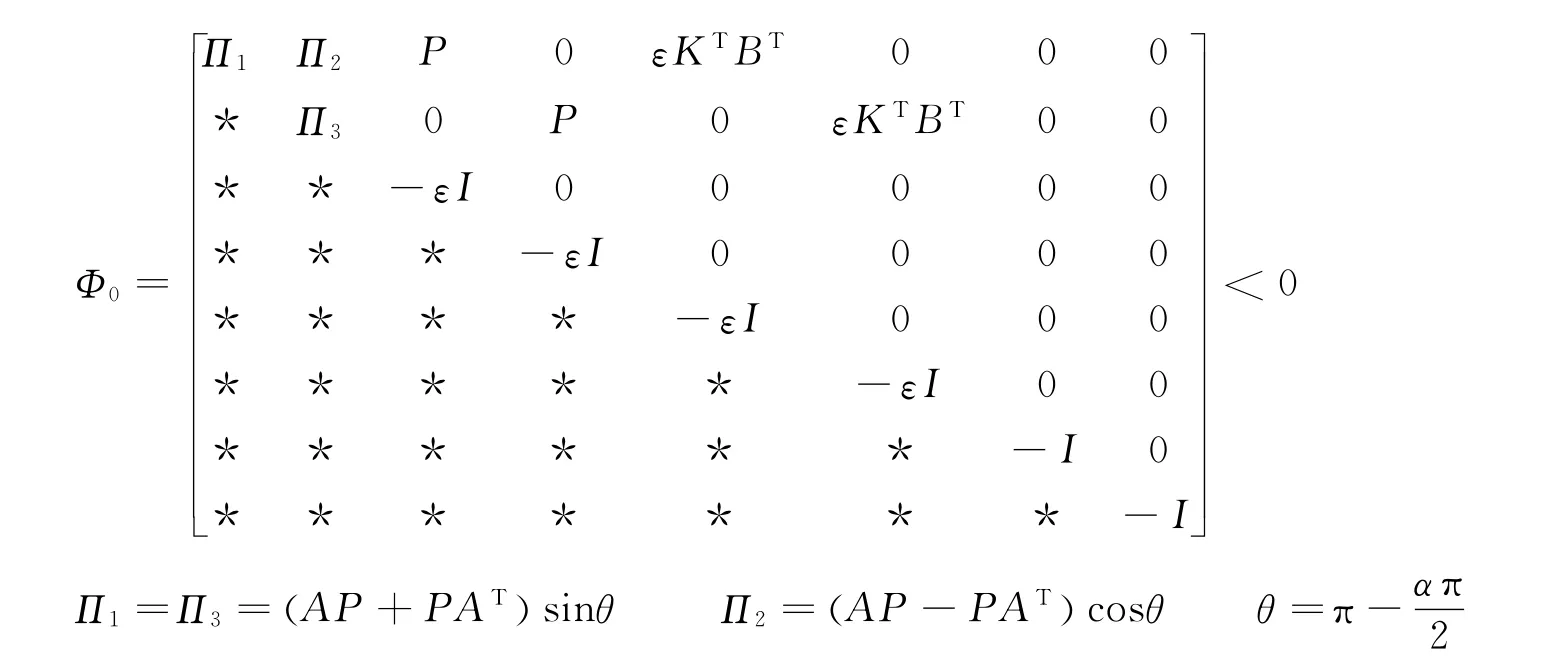
证明 由引理2可知，当下列条件满足时，系统（4）是渐近稳定的。

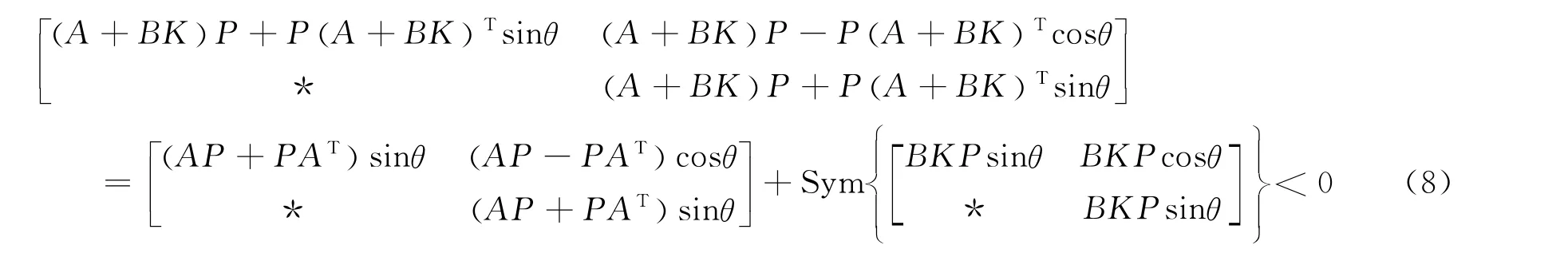
再利用引理3可得，式（8）中第2部分可以作如下分解：

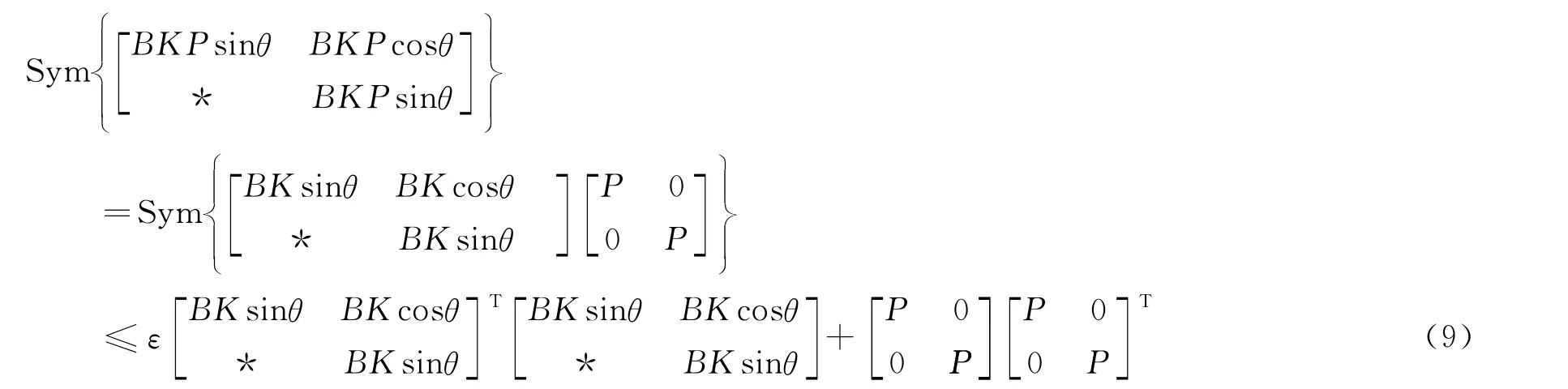
将式（9）带入式（8）中，并利用Schur补引理，可得线性矩阵不等式Φ0。证毕。

3 结语

针对阶数α的2种情况，分别用不同的方法得到系统稳定的条件。下一步可考虑系统中含有时滞情况，进一步讨论系统的稳定性条件。

［1］ 方园，蒋威 .一类分数阶时滞系统的输出反馈镇定 ［J］.信息与控制，2013，42（1）：33－38.

［2］ 方园 .分数阶时滞系统的稳定性 ［J］.阜阳师范学院学报（自然科学版），2012，29（3）：11－13.

［3］ Qian D L，Li C P，Afarwal R P，et al.Stability analysis of fractional differential system with Riemann－Liouville derivative ［J］.Mathematical and Computer Modelling，2010，52：862－874.

［4］ Lan Y H，Zhou Y.LMI－based robust control of fractional－order uncertain linear systems ［J］.Computers and Mathematics with Applications，2011，62：1460－1471.

［5］ Chilali M，Gahinet P，Apkarian P.Robust pole placement in LMI regions ［J］.IEEE Transtctions on Automatic Control，1999，44（12）：2257－2270.

［6］ Chai L，Fei S M，Xin Y B.A new type of adaptive control for time－delay systems with input delay［J］.Journal of systems science and Mathematical Sciences，2008，28（12）：1535－1544.