时间序列长度对基于ARIMA模型的月径流预报效果的影响分析

徐敏 （武汉大学数学与统计学院，湖北 武汉430072）

谢倩倩 （武汉大学深圳研究院，广东 深圳518057）

水文预报是现代水文科学的一个重要分支，其中径流预报是水文学研究的重点，即根据已有资料建立较准确反映时间序列中包含的动态依存关系的随机模型，进而对径流未来状态及变化做出预报。时间序列分析是水文预报的一个重要工具，其中Box等提出的一类有限参数型线性时间序列预测模型（Autoregressive Integrated Moving Average，ARIMA）可用于时间序列分析，由于具有简单性、可行性和对水文序列趋势的预测准确率较高的特性，其在水文预报领域有着广阔的应用前景［1］。在实际研究中，由于资料获取方面的限制，某些河段只有二三十年的月数据，在这种情况下能否建立可靠的ARIMA模型还需要深入探讨。目前，针对历史观测资料时间序列长度不足是否会产生预报误差鲜有报道。为此，笔者基于ARIMA模型，以宜昌水文站逐月径流量为例，分析时间序列长度对基于ARIMA模型的月径流预报效果的影响，以便为水文预报提供参考。

1 ARIMA模型概述

ARIMA模型（Autoregressive Moving Average，求和自回归滑动平均模型）定义如下［2］：如果一个序列｛Xt｝经过d阶差分运算后为平稳序列，而且能用ARMA模型进行平稳序列建模，则称｛Xt｝的模型结构为求和自回归滑动平均模型，简称了ARIMA（p，d，q），其具体表达式如下：

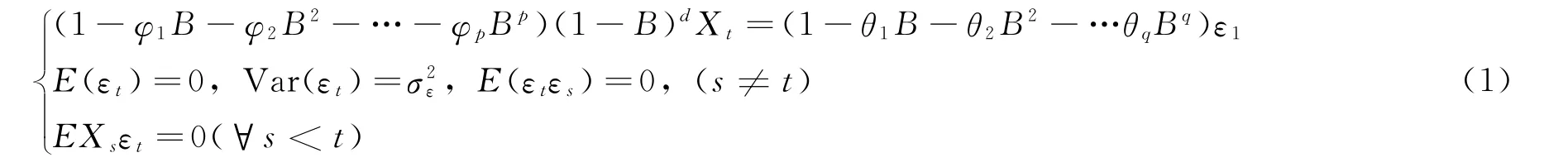
式中，p和q分别为模型的自回归（AR）阶数和滑动平均（MA）阶数；φ（B）＝1－φ1B－φ2B2－…－φpBp和θ（B）＝1－θ1B－θ2B2－…θqBq分别为自回归算子和滑动平均算子。

2 月径流ARIMA模型的建立

1）序列的去季节化 水文时间序列由于受季节因素的影响较大，表现出较强的季节变化特征，其季节均值作为确定性成分对预报有积极的作用。为此，采用剔除季节因素的方法将序列季节标准化，建立排除季节相关性影响的ARIMA模型。对于月径流数据的去季节化处理可表示如下：

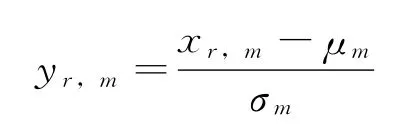
式中，r表示年份；m表示月份；μm、σm分别表示第m个月的月均值和标准差；xr，m表示第r年m月的月径流；yr，m表示去季节化后的结果。

2）数据的平稳化处理 非平稳序列经过差分提取确定性信息后，可以显示出平稳序列的性质，具体处理方法如下：对原数据分别作j次（j＝1，2，…，d）差分，综合分析其样本自相关函数和偏自相关函数的截尾性或拖尾性来确定差分次数。对差分后的序列要进行平稳性检验，基本方法包括ADF检验和 PP检验［3］。

3）模型的识别和参数估计 ARIMA模型的阶数p、q可通过样本自相关和偏自相关函数图来初步确定范围，再根据AIC准则和BIC准则选定使准则函数最小的模型为相对最优模型［1］。模型参数的估计一般采用极大似然估计法［4］，该方法利用了每一个观察值所提供的信息，估计精度高，且具有一致性的特点。

4）模型诊断检验 经过模型识别和参数估计后，还要对模型进行诊断性检验。一般通过对残差序列相关性的检验来进行判断，其中Ljung－Box方法是检验序列相关性的常用方法。Ljung－Box方法的原假设如下［2］：序列是序列m阶不相关，检验统计量记为LB，可表示如下：

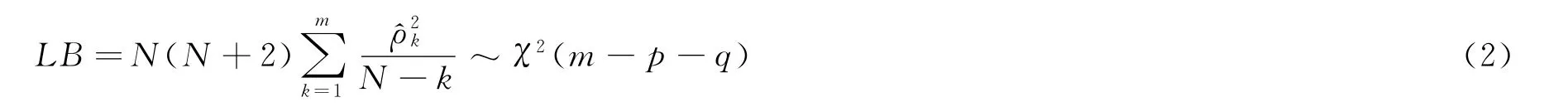
当给定置信水平1－α，若LB＜χ21－α（m－p－q），则接受原假设，认为模型通过诊断检验。

5）预报及预报效果评价 基于ARIMA模型进行月径流预报，一般采用线性最小方差预测的方法比较符合预报流域水文特性。水文序列未来某月的径流预报值等于季节均值加上由ARIMA模型预测的值。为了比较同类预测方法的时间序列长度对预测效果的影响，引入常用的预测效果评价指标如下［5］（设真实值xT＋1，xT＋2，…，xT＋l的预测值为l为预测长度，T 表示一段时间序列的开始时刻，为实测值的均值）。

①均方根误差（Root Mean Square Error）：

②绝对误差平均（Mean Absolute Error）：

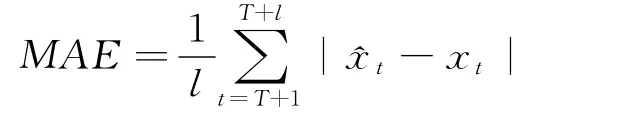
③相对误差绝对值平均（Mean Absolute Percentage Error）：

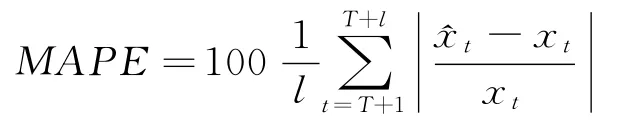
④正则均方误差（Normalised Mean Square Error）：

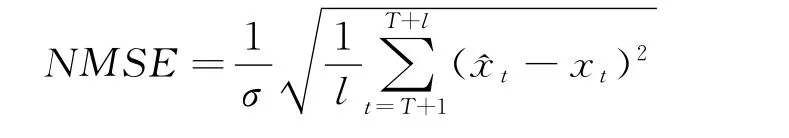
式中，σ为｛xt｝Tt＝1的标准差。

⑤确定性系数，预报值与实测值之间的吻合程度可用确定性系数作为指标，按下式计算：

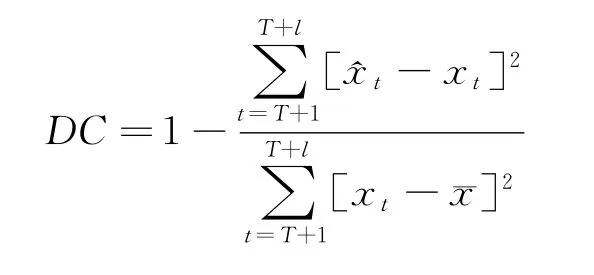
3 实例分析

宜昌水文站位于湖北省宜昌市境内，是长江三峡的出口控制站，控制流域面积100.55×104km2，占全流域面积的55%。根据宜昌水文站52年（1949～2001年）624个月径流数据，分析时间序列从2年，3年，…，52年的逐年长度变化对2001年的月径流预报效果的影响（以相对误差不超过20%为合格，月径流单位 m3／s）。

分析宜昌水文站多年月平均径流量曲线图（见图1），可以看出月径流幅度变化较大，可分为汛期和非汛期月份（6月份到10月份为汛期，7月份达到洪峰值），其中非汛期径流量较为平稳，变化不大。

通过平稳性检验和模型识别，根据AIC准则分别对1949～2000年，1950～2000年，…，1998～2000年共50组不同长度的历史月径流数据拟合适当阶数模型，并用极大似然估计法进行参数估计，模型通过诊断检验后再利用最小方差预测得到50组不同的2001年逐月径流数据的预报值。图2所示为预报结果的相对误差随时间序列长度的变化情况。

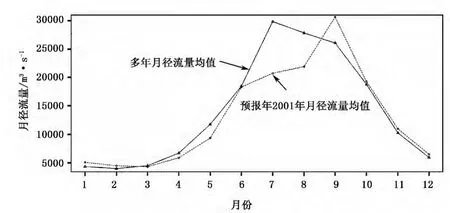
图1 宜昌水文站多年月平均径流量和预报年2001年的月平均径流量实测值曲线图

由于异常气象因素等不确定因素的影响，径流预报出现误差是不可避免的，根据径流业务预报精度评价标准，允许预报数值与实际值存在偏差：非汛期（11月至翌年5月）预报的相对误差 ，汛期（6月至10月）预报的相对误差 。从图2可以看出，在所预报的2001年月平均径流量中，预测的相对误差超过20%的仅有7月份。根据2001年湖北省水资源公报可知，2001年7月份由于气象因素异常，该月降水量出现异常，2001年湖北大部分地区出现汛期干旱，宜昌市降水量比常年偏少24.5%，与2000年比较减少30.51%，从而引起洪峰量异常。由于预报年7月份受降水异常的影响较强，因而不对7月份的预报效果进行分析。

根据水文情报规范，作业预报按每次预报误差的大小分为4个等级（许可误差可取20%的相对误差）：优（预报误差在许可误差的25%以下，即在相对误差的5%以内）；良（预报误差在许可误差的25%～50%，即在相对误差的5%～10%）；合格（预报误差在许可误差的50%～100%，即在相对误差的10%～20%）；不合格（预报误差大于许可误差，即相对误差大于20%）。

1）1月份、2月份、11月份、12月份 所有时间序列长度的预报相对误差均小于20%（基本稳定在10%左右），表明预报等级为合格，且预测精度随时间序列长度变化不大。

2）3月份 所有时间序列长度预报的相对误差均小于10%，表明预报等级为良。同时，相对误差随样本长度增加后的递减趋势较明显，即在时间序列长度小于240的范围内，相对误差在5%～10%；当时间序列长度超过240时，相对误差在5%以内；当时间序列长度大于336时，相对误差基本小于1%，当时间序列长度超过300时，相对误差保持在0.5%。因此，时间序列长度取240以上时预报较为精确。

3）4月份 当时间序列长度小于300时，相对误差精度较不稳定，在10%～20%的范围内上下浮动，表明预报等级属于合格；当时间序列长度超过300时，相对误差收敛于10%，表明预报等级属于良。

4）5月份 时间序列长度小于400时，相对误差在10%～20%内波动，表明预报等级属于合格；时间序列长度大于400时，相对误差稳定在20%，尤其当时间序列长度为24、36时，预测的相对误差在5%，表明预报等级为优，说明预报年2001年5月份的径流量与近3年该月份径流量高度相似。

5）6月份 预报情况较好，即相对误差在10%以内，尤其当时间序列长度大于72以后，相对误差在5%以内。

6）8月份 除了时间序列长度为48、60、72以外（相对误差分别达到36.2%，43.9%，37.5%），其余时间序列长度的相对误差在20%以内，表明预报等级为合格。

7）9月份 当时间序列长度小于216时，预报效果不稳定。当时间序列长度大于216时，相对误差基本稳定在20%，表明预报等级为合格。

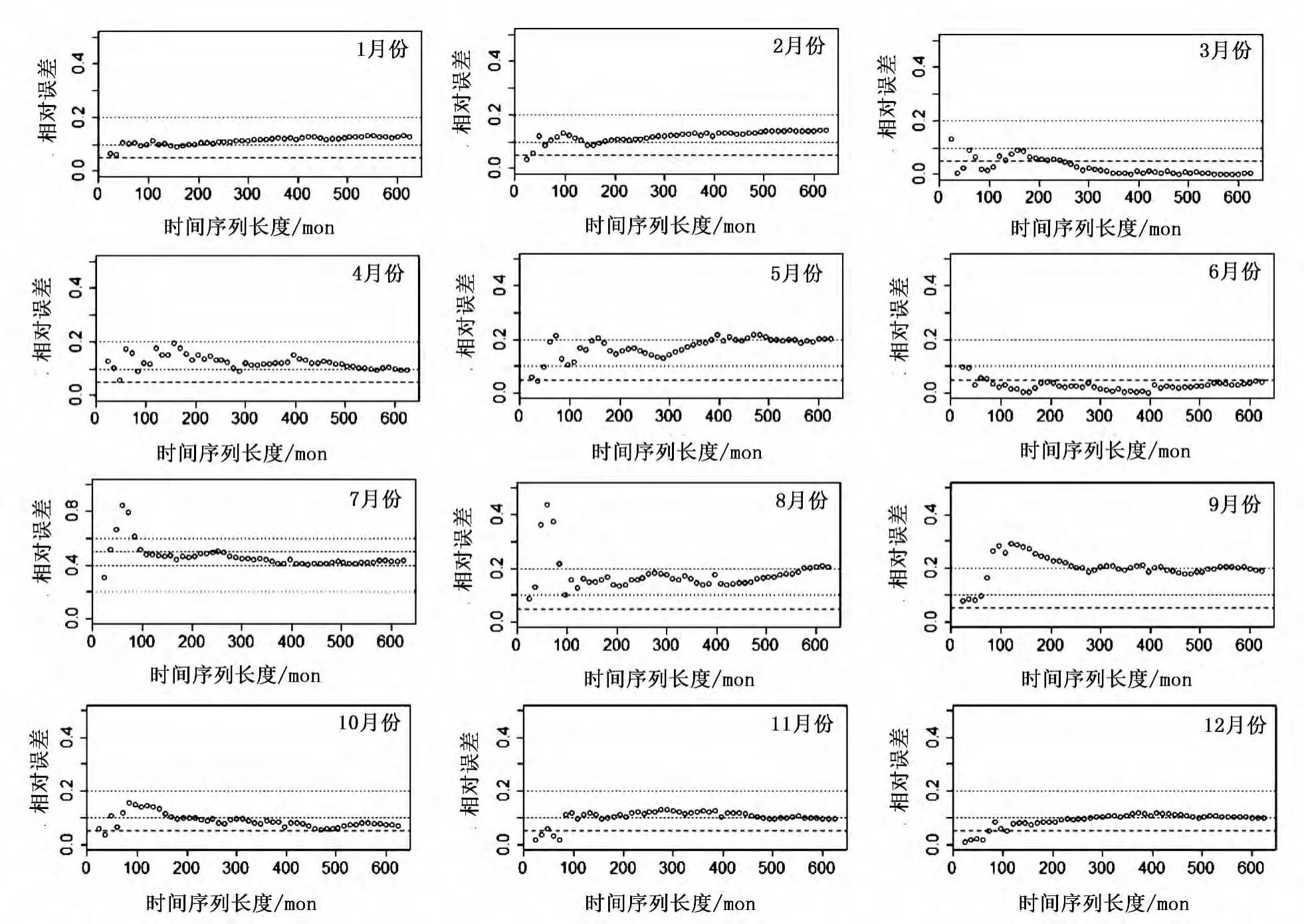
图2 2001年各月预报相对误差随时间序列长度的变化曲线图

8）10月份 当时间序列长度小于200时，相对误差精度较不稳定，在10%～20%的范围内上下浮动，表明预报等级属于合格；当时间序列长度超过200时，相对误差收敛于10%，表明预报等级属于良。

由图3可知，预测效果评价指标MAE、RMSE、MAPE、NMSE随时间序列长度的增加呈现逐渐趋于稳定状态；当时间序列长度大于200时，确定性系数DC基本稳定在80%～90%，说明预报效果较好（见图4），同时表明随着时间序列长度的增加，预报效果逐渐稳定下来。

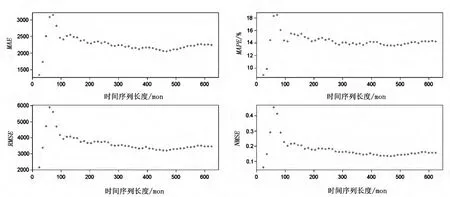
图3 预测效果评价指标随时间序列长度的变化曲线图

4 结论

1）线性最小方差预测适合用于月径流预报，尤其在非汛期的月径流预报中有较高的准确性。

2）随时间序列长度的增加，预报值的相对误差和预测评价标准MAE、RMSE、MAPE、NMSE确定性系数逐渐趋于稳定。月径流数据量不足会对预报效果产生影响，总体而言，对非汛期月份的径流预报影响较小，对汛期月份的径流预报影响较大。

3）在月径流数据量相同的条件下，非汛期月份较汛期月份的径流预报效果要好（因为只需相对较少的历史观测数据就能达到预报合格的标准），这表明对于不同月份来说，达到一定的预测效果对时间序列长度的要求是不同的。

图4 确定性系数随时间序列长度的变化曲线图

［1］ Box G E P，Jenkins A.Time Series Analysis Forecasting and Control［M］.Beijing：China Statistic Press，1997.

［2］ 王炜炘 .应用时间序列分析 ［M］.桂林：广西师范大学出版社，1999.

［3］ 章上游，林三益，黄庆宏.ARMA模型在实时水文预报中的应用探讨 ［J］.四川水力发电，1993（2）：6－14.

［4］ 王红瑞，康健，林欣，等 .水文序列ARIMA模型应用中存在的问题与改进方式 ［J］.系统工程理论与实践，2008，28（10）：166－176.

［5］ Dawson C W，Abrahart R J，See L M.HydroTest：a web－based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts ［J］.Environmental Modelling＆Software，2007，22（7）：1034－1052.