一种避免除法运算的矩阵的秩的计算方法

邓勇 （喀什师范学院数学系，新疆 喀什844006）

目前，通常采用初等行变换求解矩阵A的秩及其行空间的基，即将矩阵A化为一个行阶梯形矩阵，该行阶梯形矩阵中非零行的个数就是行阶梯形矩阵的秩。然后利用“矩阵的初等变换不改变矩阵的秩”这个结论，得到矩阵A的秩就是与其等价的行阶梯形矩阵的秩，并且行阶梯形矩阵的非零行构成了其行空间的一组基［1］。具体做法如下：设A是一个m×n整数矩阵，用初等行变换求A的秩，实际上是按下面2种基本方法分步将A化为行阶梯形矩阵。

第1种方法：用初等行变换将A的第一列中除第一个元素外的其他所有元素都化为0。

第2种方法：先用左上角元素a11除第一行所有元素（假设a11≠0），然后其他所有行减去第一行的适当倍数，将第1列中除第1个元素（实际上是1）外的其他所有元素都化为0。

这2种计算方法的最终目的就是为了把矩阵A化成形如：

的矩阵。这时有：

上述2种方法的一个共同特点就是需要对矩阵中的数字做大量除法运算，导致计算中会出现很多分数，潜在的运算错误会迅速增加，同时，究竟使用哪些行操作可减少计算量也具有不确定性。基于上述原因，笔者总结出一种不做除法运算就可求得矩阵秩的方法。

1 算法

设P是一个数域，Pm×n是数域P上的m×n矩阵集合，～表示矩阵的等价。对任何一个矩阵A＝（aij）∈Pm×n，当其元素aij的任何一对下标i、j满足2≤i≤m、2≤j≤n时，可定义2×2子行列式：

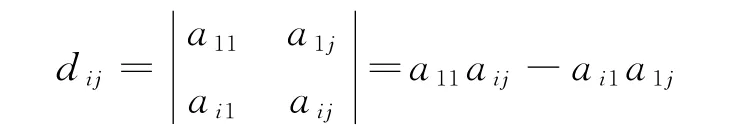
定理1 设A＝（aij）∈Pm×n，且a11≠0，则：

证明 用a11分别乘第2行到第m行，得到：

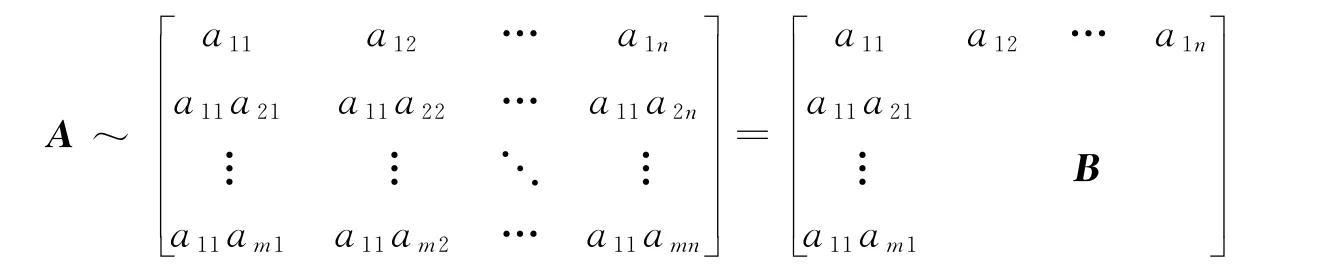
在矩阵B中，由于它的行标i和列标j分别满足2≤i≤m，2≤j≤n，所以再用ai1乘以第一行后减去后面的第i行（i＝2，3，…，m），得到：

因为a11≠0，所以：

按照定理1，可以得到不做除法运算来求矩阵A的秩的算法。算法的具体步骤如下：

1）如果给定非零矩阵A＝（aij）m×n的第一列元素全为0，那么删去这一列后，矩阵的秩不会改变。2）假设A＝（aij）m×n的第1列是非零列。不失一般性，设a11≠0。利用初等行变换将A化为与之等价的矩阵于是

2 具体算例

解

阵行空间的一组基。即：

3 几点说明

1）在求矩阵A行空间的一组基时，笔者用初等行变换建立起了一个与A等价的行阶梯形矩阵，而这个行阶梯形矩阵的非零行就构成了原矩阵行空间的一组基。因此，在建立这个行阶梯形矩阵中，必须注意重新插入在计算矩阵秩的过程中被删除的所有零列。

2）设A是一个n×n矩阵。如果把一个k×k矩阵减少为一个（k－1）×（k－1）矩阵，那么需要做2（k－1）2次乘法。当k从2增加到n时，对A共需要做次乘法，它与计算A的行列式所需要的计算量是相同的。

［1］ 张禾瑞，郝炳新 .高等代数 ［M］.第4版 .北京：高等教育出版社，1999：127－136.

［2］ 齐民友，蔡德祺，刘丁酉 .线性代数 ［M］.北京：高等教育出版社，2003：72－81 .