不同水平女子马拉松运动员的节奏策略研究

杨 锋，朱 瑜，高 岩，3

1 前言

马拉松是总距离为42.195km的周期性耐力项目，超长的运动时间与运动距离要求运动员具备很强的氧代谢能力、适时放松的能力以及经济的体力分配［6，10］。马拉松运动员取得优异成绩受到多种因素的影响，其中，适宜的节奏控制有利于其发挥出个人最佳成绩。因此，在比赛全程中的速度控制与节奏分配是否符合项目特点，是否符合自身训练水平对最终成绩起着决定性作用［11，12］。体力分配战术是运动员在比赛全程中根据自身训练水平进行合理体力分配获得优异成绩（包括成绩与名次）的战术行动，根据参赛目的还可细分为创造记录战术和夺名次战术［6］。

目前，国内、外诸多研究将运动员在训练、比赛中调节工作强度、分配能量的认知概念称为“节奏策略（Pacing Strategy）”，且定义为，在不对生理系统造成不可逆伤害的前提下，为了达到最优化运动表现的一种对能量输出调控［1，7，19］的意识或者潜意识，它包括消极性节奏策略、全冲节奏策略、积极性节奏策略、均匀节奏策略、抛物线型节奏策略及变异型节奏策略［1，3，16］，并根据项目特点而相应地应用。虽然每个马拉松运动员都有自身特色的节奏策略［25］，但许多研究者仍然发现了一些共性规律，比如马拉松比赛各分段速度变异不大，总体上有“匀速跑”特征［4，11，12］。但近年来的多项研究表明，匀速跑是相对的，比赛全程中的局部分段速度仍呈现出波浪式的上升、下降，特别是途中阶段和终点阶段［10，20］，并且30km、35km 阶 段速度下降较多［4］，表现出类似于“W”的波浪式变化。

运动员速度节奏的自我控制既受生理机能因素的作用，也受到心理因素的影响。运动员在比赛过程中对自我努力感（RPE）［30］、自我时间预期（ELT）［23］和领先运动员表现［18，24］的认知以及对冲击名次还是个人最好成绩等比赛结果的期望都会影响运动员速度节奏的自我控制。对于以夺名次为参赛目标来说，领先运动员的实力形成强烈的心理暗示进而干扰运动员的节奏控制［20］。也有一项实验室研究认为，领跑对运动成绩、心率（HR）、RPE的影响不显著［24］，但是，基于实验室研究设计的运动员、测试人员缺乏对奥运会、世界锦标赛这样的国际重大赛事比赛结果的强烈期望，因而，它关于“领跑作用”的研究结果适用性有限。

目前，国内对节奏策略的研究有不少，对前3名、前8名、前10名运动员甚至对一些优秀运动员的个案研究较多［2，4，10－12］，而 对 于 未 获 得 好 名 次 ，尤 其 是 有 竞 争 实 力 却 未取得相应比赛成绩的运动员的节奏策略研究却很少。通过分析2012年伦敦奥运会不同水平女子马拉松运动员在比赛中所表现出来的节奏策略，重点分析获得好名次的运动员与没获得好名次运动员节奏控制策略的差异和影响因素，为我国青少年、成年马拉松运动员的训练计划、参赛方案提供参考。

2 研究对象与方法

2.1 研究对象

参加2012年伦敦奥运会女子马拉松比赛运动员的成绩，包括5km分段成绩（Split time）、最后2.195km分段成绩、最终成绩（Finish time）和个人最佳成绩（PB time）。2012年伦敦奥运会女子马拉松比赛共有107名运动员参加，其中，在国际田径联合会官网上（www.iaaf.org）查到个人最佳成绩（PB time）的有89名，剔除了1名个人最好成绩和比赛成绩相差1 100s、年龄42岁运动员的成绩，共88名运动员。

2.2 研究方法

2.2.1 研究假设

个人最佳成绩可以体现出运动员竞技水平的高低。比赛中，运动员的竞技表现又受到个人最佳成绩的影响，因此，不同水平运动员比赛成绩的差异与个人最佳成绩之间的差异就应有较好的拟合度。适宜的节奏策略是保证运动员重现个人最佳成绩的重要因素［16，20］，所以，在理论上认为不同水平运动员的节奏策略应该相当。

基于此理论构想提出研究假设，假设1：不同水平女子马拉松运动员间个人最佳成绩变异程度与比赛成绩变异程度没有差异；假设2：不同水平女子马拉松运动员分段速度节奏（节奏策略）没有差异。

2.2.2 实验设计

采用前实验研究被试间事后准则多样组设计［5，12］，将88名运动员按比赛名次平均分配到4个分组作为自变量，每组22名，收集每组个人最佳成绩（PB time）和奥运会比赛成绩（Race time）。

计算每组个人最佳成绩（PB time）、奥运会比赛成绩（Race time）的“绝对平均速度”、奥运会比赛速度对于个人最佳成绩速度的保持比作为“相对平均速度”以及各分段“绝对平均速度”、“相对平均速度”和“全程分段速度”相对于第1个5km分段速度的变异量。

2.2.3 数据统计

运用SPSS 20.0软件统计计算成绩变量、速度变量、变异系数，并检验相关性、差异显著性，统计显著性水平α接受于P＜0.01。

1.用皮尔逊积差相关系数（Pearson produce－moment correlation）分析个人最佳成绩与比赛成绩的相关性；

2.单因素方差分析（One－way analysis of variance）检验各组个人最佳成绩速度与比赛速度的差异显著性，包括Bonferroni事后检验（Bonferroni post hoc test）进行两两比较、计算组间偏eta方η2p（Partial eta－squared）；

3.用Cohen’s d系数计算两组之间差异的效果量，小于0.2效果量小、接近0.5效果量适中，大于0.8效果量较大［13］。η2p计算组间自变量对因变量变异的解释程度，小于0.1效果量小，0.25左右效果量中等，大于0.4效果量大。

计算公式：

3 结果与讨论

3.1 不同水平女子马拉松运动员个人最佳成绩与奥运会比赛成绩差异

3.1.1 数据方差齐性、正态分布检验

统计学的方法有许多种，没有哪种方法是通用的，应用方差分析时，数据应当满足独立性、方差齐性假设和正态分布假设［14］。被试运动员的比赛成绩之间相互独立，没有相关关系保证其独立性。

表1显示，个人最佳成绩速度（PB Speed）与奥运会比赛速度（Race Speed）在独立性、方差齐性、正态分布检验上符合方差分析的应用条件（P＞0.05）。

表1 2012年伦敦奥运会比赛成绩与运动员个人最佳成绩数据（1～4组方差分析）假设检验一览表Table 1 Data of Personal Best Result of Marathoner in London Olympic Games

3.1.2 伦敦奥运会比赛运动员个人最佳成绩重现能力分析

个人最佳成绩是运动员当前所参加比赛中取得的最高成绩，运动员在比赛中取得的成绩越接近个人最佳成绩（甚至超过），就越证明运动员发挥了自身潜力。2012年伦敦奥运会女子马拉松比赛，比较4组比赛成绩组间变异与个人最佳成绩组间变异可以反映出不同水平女子马拉松运动员个人最佳成绩的重现能力。

图1显示，1～4组运动员的个人最佳成绩平均速度为4.90m／s、4.76m／s、4.68m／s和4.57m／s。经方差检验（表2），1～4组组间差异具有显著性（P＜0.01），组间差异解释量大（η2p＝0.521），其中，第1组显著快于第2、3、4组（全部P＜0.01，效果量为1.37、2.09、2.73），第2组显著快于第4组（P＜0.01，效果量为1.48）。

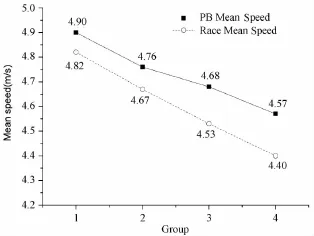
图1 本研究4组运动员个人最佳成绩平均速度、奥运会比赛平均速度示意图Figure 1. PB Mean Speed and Race Mean Speed of Group 1－4

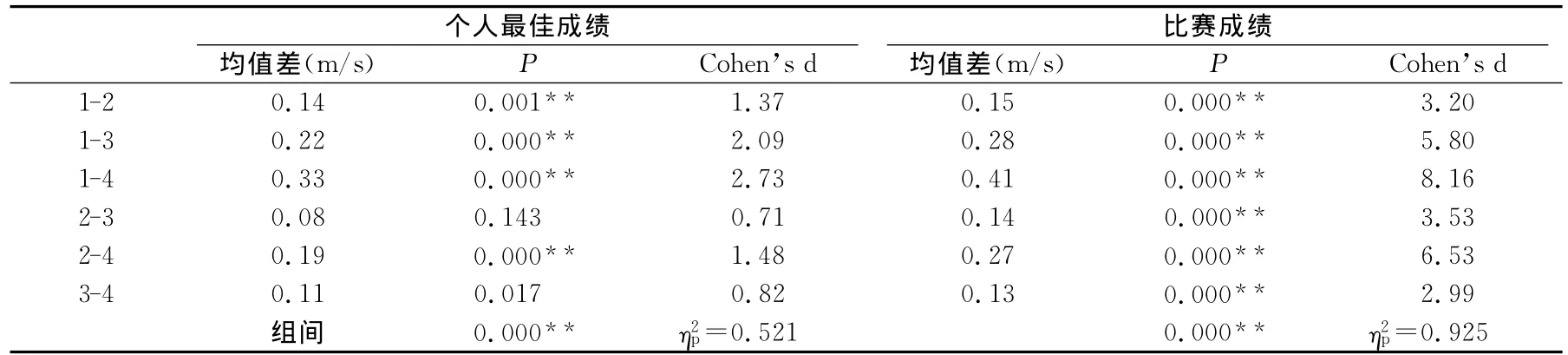
表2 本研究4组运动员个人最佳成绩与奥运会比赛成绩检验结果一览表Table 2 Statistics of Personal Best Result and Race Test Result of Group1－4

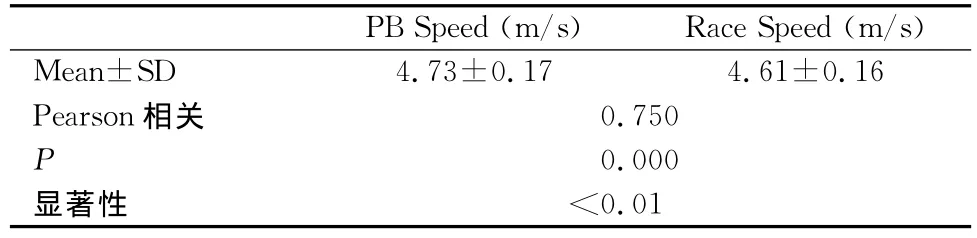
表3 伦敦奥运会成绩与运动员个人最佳成绩相关性检验统计一览表Table 3 Statistical Correlation Test of Marathon Performance and Marathoner Personal Best Result of London Olympic Games（n＝88）

比赛成绩平均速度为4.82m／s、4.67m／s、4.53m／s和4.40m／s。经方差检验（表2），差异具有显著性（P＜0.01）组间差异解释量非常大（η2p＝0.925），其中，第1组显著快于第2、3、4组（全部 P＜0.01，效果量为3.20、5.80、8.16）；第2组显著快于第3、4组（P＜0.01，效果量为3.53、6.53）；第3组显著快于第4组（P＜0.01，效果量为2.99）。

从折线图趋势、均值差等统计结果显示，1～4组个人最佳成绩、奥运会比赛成绩组间都表现出下降趋势，但下降的幅度不一致。经检验（表3），个人最佳成绩与比赛成绩相关系数高达0.75（P＜0.01），且组间η2p值差异大（比赛成绩、个人最佳成绩组间η2p为0.925、0.521）、比赛成绩各组Cohen’s d值差距幅度大于个人最佳成绩。因而，可以认为，比赛成绩组间下降幅度更大，趋势更加明显，这说明，比赛中获得好名次运动员的成绩比其他运动员更加接近于个人最佳成绩。

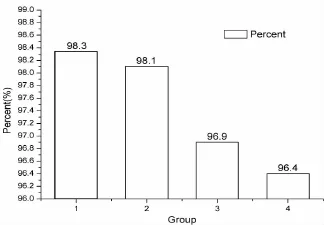
图2 本研究4组运动员奥运会比赛成绩速度与个人最佳成绩速度比例柱状图Figure 2. Diagram of Ratio between Race Speed and Personal Best Speed of Group 1－4

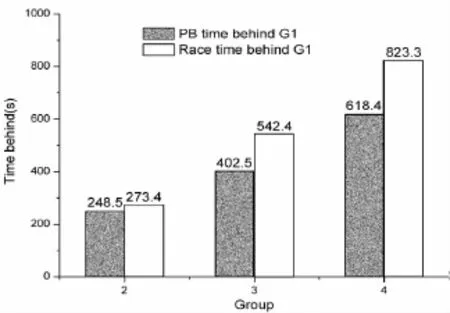
图3 本研究第2～4组运动员个人最佳成绩和奥运会比赛成绩与第1组落差柱状图Figure 3. Diagram of Difference between Personal Best Speed and Race Result of Group 2－4and Group 1

图2、图3显示，1～4组奥运会比赛成绩平均速度相对于个人最佳成绩平均速度比例分别为98.3%、98.1%、96.9%和96.4%。第1组运动员的比赛成绩平均速度最接近于个人最佳成绩平均速度；第2组平均个人最佳成绩、奥运会比赛成绩落后于第1组248.5s、273.4s，差值为24.9s；第3组为402.5s、542.4s，差值为139.9s；第4组为618.4s、823.7s，差值为205.3s。

统计结果显示，第2、3、4组奥运会比赛成绩落后于第1组的幅度比个人最佳成绩落后的幅度要大得多，数据显示，第3、4组比赛中重现个人最佳成绩的能力远远落后于第1、2组，这必然会导致比赛中名次的落后。假设第2～4组的比赛成绩都能像第1组实现个人最佳成绩98.3%的重现度，那么，第2～4组的比赛成绩将会分别提高16.5s、129.8s、191.3s，随之比赛运动成绩的提高也必然使比赛名次得到提高。

3.2 伦敦奥运会女子马拉松比赛运动员节奏策略特征分析

3.2.1 5km分段平均速度节奏控制分析

有研究表明，成功的运动员比其他运动员取得更优异的运动成绩是由于他们的比赛成绩更加接近于个人最佳成绩，产生这一现象的原因是采用更成功的节奏策略［20］。2012年伦敦奥运会女子马拉松比赛成绩优异或者超常发挥的运动员，或许采用了比其他运动员更适宜的节奏策略而取得接近、甚至超越个人最佳成绩的运动成绩。通过研究马拉松比赛5km分段平均速度变化可以揭示出比赛中运动员所采用的节奏策略。

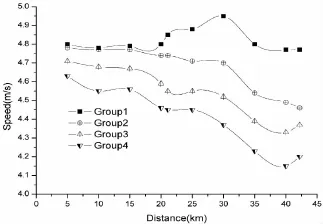
图4 本研究4组运动员5km分段速度节奏策略曲线图Figure 4. Diagram of 5km Sectional Speed Pacing Strategy of Group 1－4

图4、表4显示，第1组从比赛出发到终点各5km分段的绝对平均速度高于第2、3、4组（其中，0～20km分段第1组显著快于第3、4组且P＜0.01，20km～终点分段第1组显著快于第2、3、4组且P＜0.01），并且随着比赛的进行差距越来越大。1～4组各5km分段速度相对于比赛平均速度的变异量分别为0.96%、2.3%、2.52%和3.23%。可见，第1组前半程与后半程之间的波动相对较小，第2、3、4组都表现出递增的、不同程度的波动。第1组在5km、5～10km、10～15km 3个分段低于比赛成绩平均速度，而第2、3、4组却高于比赛成绩平均速度，经检验，第1组平均速度保持率与第2、3、4组存在显著性差异（P＜0.01，平均Cohen’s d为2.66、2.49、2.02，组间η2p为0.57、0.48、0.34），在15～20km、20～25km两个分段和平均速度基本相当，与第2、3、4组不存在显著性差异（P＞0.05），在25～30km、30～35km、35～40km仍保持较高的速度水平，而第2、3、4组却明显低于平均速度，第1组与第2、3、4组存在显著性差异（P＜0.01，平均Cohen’s d为1.4、1.49、1.16，组间η2p为0.26、0.30、0.20）。

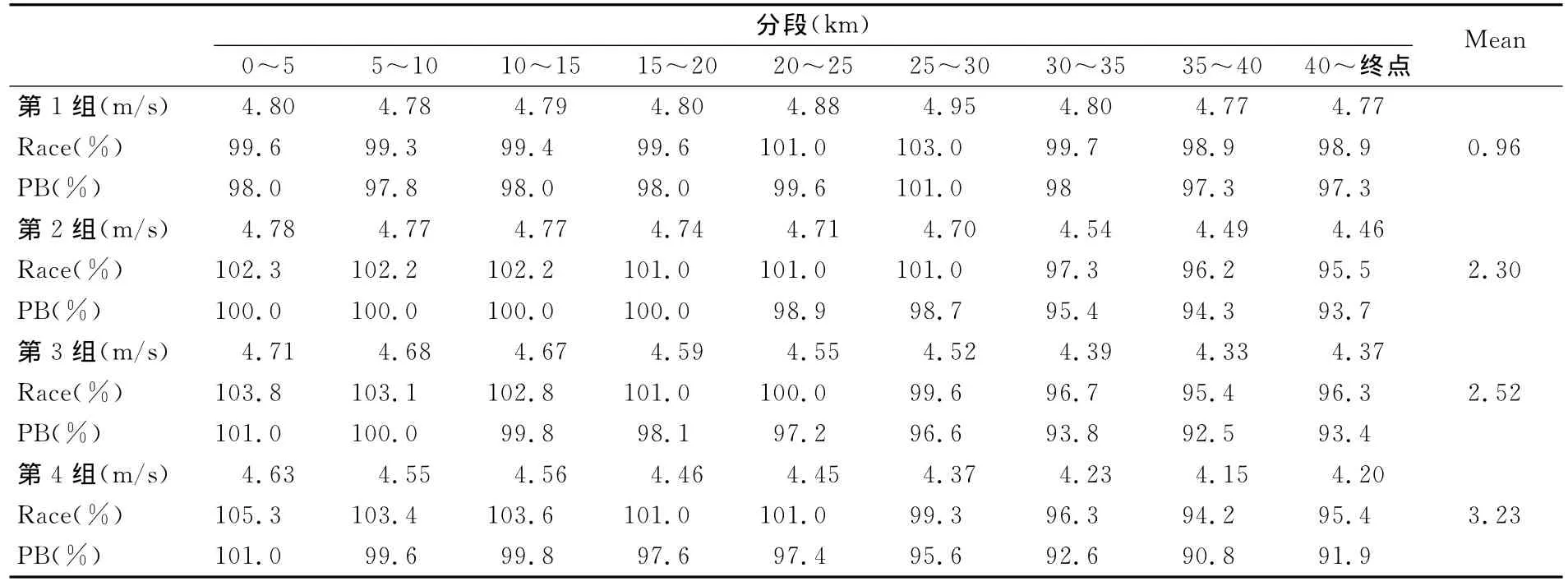
表4 本研究4组运动员5km分段速度相对于个人最佳成绩、奥运会比赛成绩平均速度变异统计一览表Table 4 Statistical Variation of 5km Sectional Speed Relative to the Personal Best Average Speed and Race Average Speed of Group1－4

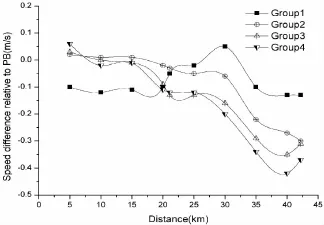
图5 本研究4组运动员5km分段速度相对于个人最佳成绩平均速度差值曲线图Figure 5. Diagram of Difference between 5km Sectional Speed Relative to the Personal Best Average Speed of Group 1－4

图5、表4显示，尽管第1组前半程平均速度高于第2、3、4组，但是却低于其个人最佳成绩平均速度。第1组运动员在0～5km、5～10km，10～15km、15～20km分段平均速度占个人最佳成绩平均速度比例为98%、97.8%、98%、98%，特别在比赛初始0～5km、5～10km、10～15 km的3个分段，是4个组中最低的（P＜0.01，与第2、3、4组的 平 均 Cohen’s d为 1.41、1.1、0.96，ηp2 为 0.26、0.18、0.14），然而，20～25km、25～30km、30～35km、35～40km分段却提高了跑速，持平甚至稍微超过了个人最佳成绩平均速度，在4个组中是最高的（P＜0.01，平均Cohen’s d为 0.89、1.49、1.41、1.07，η2p为 0.20、0.35、0.29、0.20）。

通过数据挖掘分析发现，第2、3、4组运动员比赛成绩的落后除了因为竞技状态的差距之外，还存在节奏策略选择上的错误。第1组运动员全程速度变异小，前半程分段平均速度低于比赛平均速度、个人最佳成绩平均速度，后半程分段高于比赛平均速度、持平甚至高于个人最佳成绩平均速度，但是，第2、3、4组的节奏刚好相反，且第3、4组在后半程还表现出更明显的下降。从比赛全程的角度看，第2、3、4组运动员选择了不适宜的初始速度，进而导致了后半程速度的大幅度下降，特别是在30km之后的分段，这形成了积极性节奏（Positive Pacing）。积极性节奏是一种全程速度逐渐下降的节奏策略，在短距离游泳如100 m、200m 泳［29］和田径800m跑［28］中经常看到以 用 于 保 证初始阶段的高速和加速。对于长距离耐力项目如马拉松、竞走等，这类项目能量消耗时间长、输出功率相对低，在初始阶段应该避免超出身体负荷的高速。在中、长距离跑中，为了战术和创造优异运动成绩的需要，较多采用一种类似于“J”、“U”型节奏策略，用来保证最后阶段的加速同时又避免过高的初始速度引起的生理动态平衡失调［16，26］。第1组运动员的节奏表现出了类似“J”、“U”的抛物线型节奏策略，前半程保持稍微低于个人最佳成绩的平均速度，进而使得后半程25～30km分段出现积极加速，在35km之后分段以不低于全程平均速度的节奏完成比赛。第2、3、4组都表现出了“积极性节奏”的特征，前半程（特别是前3个分段）以高于个人最佳成绩的速度比赛，导致供能系统、神经系统等生理系统的紊乱，引起后半程跑动速度的下降。

3.2.2 4组运动员各5km分段相对于第1个5km分段的速度变异分析

节奏策略从运动员比赛全程速度变化中表现出来，初始速度的高低直接影响后程的竞技表现，比较各5km分段相当于第1个5km分段的速度变异能更准确地揭示运动员初始阶段的节奏策略特征。

图6、表5显示，总体上，第1组运动员各5km分段速度与第1个5km保持均衡，20～25km、25～30km甚至高于第1个5km，而35～40km、40km～终点分段也仅慢0.03m／s；第2组运动员除了5～10km、10～15km基本与第1个5km持平外，其余各分段都显著慢于第1个5 km，在30km分段之后出现了渐进的速度大幅下降；第3、4组各5km分段都显著慢于第1个5km分段，在15～20 km开始就出现幅度较大的下降，而且后半程下降幅度更加明显。从后半程的数据来看，第2、3、4组在30～35 km、35～40km、40km～终点分段都表现出显著下降，平均下降0.28m／s、0.35m／s、0.44m／s，而第1组在后半程的变化仅平均降低0.02m／s，相对于第1个5km几乎没有出现速度下降。

可以看出，第2、3、4组相对于第1个5km分段的其他各5km分段速度变异值明显高于第1组。经检验，除了10～15km分段，其他分段组间存在显著性差异（P＜0.01，为 0.284、0.322、0.533、0.535、0.478、0.369、0.212），其中，第1组5～10km与第4组存在显著性差异（P＜0.01，Cohen’s d＝0.49），15～20km与第3、4组存在显著性差异（P＜0.01，Cohen’s d为1.17、1.47），20～25 km、25～30km、30～35km、35～40km、40km～终点都与第2、3、4组存在显著性差异（P＜0.01，平均 Cohen’s d为2.57、2.35、2.20、1.73、1.12），很明显，第1、2、3、4组随着比赛的进行，全程的、组间的各分段速度变异逐渐增大。

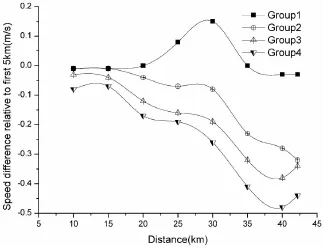
图6 本研究4组运动员5km各分段相对于第1个5km速度差值曲线图Figure 6. Diagram of Difference of 5km Sectional Speed Relative to First 5km Speed of Group 1－4

表5 本研究4组运动员5km各分段与第1个5km速度变异统计一览表Table 5 Statistical Variation of 5km Sectional Speed Relative to First 5km Speed of Group 1－4 （m／s）

终点冲刺阶段是比赛最后阶段，许多运动员在这个阶段往往会忽略生理动态平衡失调，选择保持高速来完成比赛［15］。从统计结果看，所有组运动员在30～35km分段的速度都出现了下降，其中，第1组运动员在30～35km分段将速度降到与第1个5km分段差不多的水平（这里可以认为是最适宜的水平），随后保持这一高速完成终点冲刺；第2组前半程保持与第1个5km分段基本相当的速度，在30～35km分段将速度下降，以保证终点阶段的速度不至于下降过多，如果能在第1、2个5km调整降慢跑速，可能就不会出现后半程的速度下降过大，进而提高全程平均速度，冲击第1组运动员。虽然第1、2组在终点冲刺前的30～35km都表现出了较大幅度的下降，但是，终点阶段的速度基本保持平稳或略微下降，而第3、4组却反而出现加速现象。可以认为，第3、4组运动员的30～35 km速度下降幅度大，而在35～40km分段进行节奏调整。整体上看，第3、4组运动员初始阶段速度过快，导致后半程速度下降过大，就出现了节奏的过度调整。

肌肉活动的调节与控制除了受生理机能应答的影响外 ，还 受 环 境 因 素 和 认 知 因 素 的 影 响［9，17，18］。 同 一 场 比 赛的外部环境对于每一个运动员都是相同的，运动员自身的认知心理因素也会影响运动员对节奏的控制。奥运会比赛时运动员采用的节奏策略与获得个人最佳成绩时是不一样的［22］，像奥运会这样的国际重大比赛，有时候名次比成绩更有意义，而且，大多数运动员是得不到奖牌的，尤其是金牌，所以，运动员从竞赛动机上说，是不太愿意做领跑人或者超过个人最佳成绩的平均速度领跑。第1组运动员选择低于个人最佳成绩的初始速度应该有战术上的考虑。在参赛动机与战术选择上，有研究认为存在性别差异，男运动员比女运动员更愿意展示自身的竞技水平，而女运动员的策略性更强，所以，性别可能会造成节奏策略的 选 择 性 差 异［20，21］。

运动员既不能在比赛完成前将能量消耗殆尽而导致生理机能紊乱，也不应该在比赛完成后还保留过多体能，因而，运动员在比赛中需要在初始速度的选择和维持生理机能之间博弈。比赛中若有运动员领先于自己，运动员倾向于做出跟随的决策，特别是当运动员认为对手可能比自己获得更好的名次或者成绩的时候［20］。虽然有实验研究认为，领跑对运动成绩的作用不显著［24］，但是，在实验室研究中的运动员缺乏对比赛结果的强烈期望，尤其像奥运会、世界锦标赛这样的国际重大赛事。由于未考虑到动机因素，所以该研究结果的适用性是非常有限的。在实际比赛中，由于对手干扰，运动员的领跑导致节奏控制紊乱的情况屡屡出现，这可能是导致第2、3、4组运动员根据第1组运动员速度而选择过高初始速度的原因。

避免后半程降速，特别是35km以后速度耐力以及保持高速的能力是马拉松制胜的重要因素［8，11］。虽然，第2、3、4组运动员在初始阶段选择了较高初始速度，使得0～5 km、5～10km分段高于个人最佳成绩的平均速度，但后半程出现大幅度的下降却致使整体平均速度低于个人最佳成绩时的速度，可能是缘于自身竞技水平的不足导致比赛冲刺前的30～35km分段出现了生理机能紊乱而速度大幅下降，从而影响了运动成绩和比赛名次。尽管每个运动员都有自己的最优节奏策略，但从1～4组个人最佳成绩的差异和第2、3、4组在比赛中速度的变异可以推断，他们选择的节奏策略是不太适合自己的，至少不是最优化的，比如初始阶段过高的速度策略、冲刺阶段前的过度调节策略等。

4 结论

1.名次靠前的运动员重现个人最佳成绩的能力强于名次靠后的运动员。4组运动员奥运会比赛成绩的组间差距大于个人最佳成绩的组间差距，与第2、3、4组相比，第1组运动员获得了更加接近于个人最佳成绩的比赛成绩。

2.运动员获得优异比赛成绩除了身体训练水平之外，还因为选择了适宜项目特点的节奏策略。第1组与第2、3、4组运动员的全程速度表现出不同的节奏策略，第2、3、4组表现出前快后慢的“积极性节奏策略”，而第1组采用了更符合马拉松项目特点的“J”型抛物线型节奏策略。

3.第1组选择了更适宜的初始速度，避免了后半程的速度下降。相对于第1个5km分段，第1组的后半程为正向变异，而第2、3、4组前、后半程出现了负向变异，并且变异随着名次的落后级别而增大，同时，第3、4组运动员的最后2.195km速度还出现了上升趋势，说明第3、4组运动员后半程的速度控制出现了过度调节。

4.战术考虑、环境认知等心理因素影响了运动员节奏策略的选择。4组运动员在比赛初始阶段、终点阶段都有基于战术、认知方面的速度改变，并影响了比赛成绩。比赛中，未获得前几名的运动员，以个人最佳成绩为基准，其身体训练水平与前几名没有多大差距，如能采用更适合的节奏策略，也许能提高比赛名次，而第3、4组类型的运动员，如果采用更平均、更适宜的节奏策略，也许能在运动成绩和名次上超过身体训练水平高，但是节奏控制不好的其他运动员。

［1］鲍政栋，姒刚彦，蒋小波.“节奏策略”的原理与运用［J］.体育科学，2007，27（8）：79－85.

［2］陈仁伟.我国优秀马拉松运动员李柱宏训练特点的分析［J］.中国体育科技，2005，41（3）：53－55.

［3］郜卫峰.计时类运动项目速度节奏的类型及应用［J］.体育科学，2011，31（5）：91－97.

［4］焦芳钱，刘大庆.我国女子马拉松训练理论研究综述［J］.中国体育科技，2008，44（4）：36－65.

［5］肯尼斯S博登斯，布鲁斯B阿博特（著），袁军（译）等.研究设计与方法［M］.上海：上海人民出版社，2008：241－293.

［6］李老民.田径运动教程［M］.北京：北京体育大学出版社，2008：248－249.

［7］苏志雄，黄志剑，蒋小波，等.节奏策略中枢控制的实验验证［J］.中国运动医学杂志，2010，29（1）：8－13.

［8］佟胜志.国家女子马拉松队外教罗萨训练理念探究［J］.北京体育大学学报，2011，34（8）：139－141.

［9］武雪莲.气象条件对马拉松成绩影响的研究［J］.中国体育科技，2012，48（5）：16－20.

［10］谢慧松，袁荣凯，周铁民.对我国优秀女子长跑运动员10 000m跑分段速度的研究［J］.北京体育大学学报，2004，27（6）：846－855.

［11］于奎龙，吴长稳.第29届奥运会马拉松运动员速度分配特征的研究［J］.首都体育学院学报，2009，21（6）：756－758.

［12］翟丰.优秀马拉松运动员比赛速度分配与模式建立的研究［J］.天津体育学院学报，2006，21（1）：63－66.

［13］张力为.体育科研方法［M］.北京：高等教育出版社，2002：152－169.

［14］张文彤，邝春伟.SPSS统计分析基础教程（第2版）［M］.北京：高等教育出版社，2011：263－275.

［15］A ST CHAIR GIBSON，T D NOAKES.Evidence for complex system integration and dynamic neural regulation of skeletal muscle recruitment during exercise in humans［J］.Brit J Sport Med，2004，38（6）：797－806.

［16］ABBISS CHRIS R，LAURSEN PAUL B.Describing and understanding pacing strategies during athletic competition ［J］.Sports Med，2008，38（3）：239－252.

［17］ABBISS CHRIS R，LAURSEN PAUL B.Models to explain fatigue during prolonged endurance cycling ［J］.Sports Med，2005，35（10）：865－898.

［18］ALAN S T CHAIR GIBSON，ESTELLE V LAMBERT，LAURIE H G RAUCH，et al.The role of information processing between the brain and peripheral physiological systems in pacing and perception of effort［J］.Sports Med，2006，36（8）：705－722.

［19］ANSLEY L，SCHABORT E，ST CHAIR GIBSON A，et al.Regulation of pacing strategies during successive 4－km time trials［J］.Med Sci Sport Exe，2004，36（10）：1819－1825.

［20］ANDREW RENFREE，ALAN ST CHAIR GIBSON.Influence of different performance levels on pacing strategy during the women＇s world championship marathon race ［J］.Int J Sport Physiol，2013，8（3）：279－285.

［21］BERND FRICK.Gender differences in competitive orientations：empirical evidence from ultra marathon running ［J］.J Sport Econ，2011，12（3）：317－340.

［22］CHRISTIAN THIEL，CARL FOSTER，WINFRIED BANZER，et al.Pacing in olympic track races：competitive tactics versus best performance strategy ［J］.J Sport Sci，2012，30（11）：1107－1115.

［23］COQUART JEREMY B，ESTON ROGER G，NOAKES TIMOTHY D，et al.The estimated time limit：a brief review of a perceptually based scale［J］.Sports Med，2012，42（10）：845－855.

［24］DERYN BATH LOUISE A，TURNER ANDERW N，BOSCH ROSS TUCKER ESTELLE V，et al.The effect of a second runner on pacing strategy and RPE during a running time trial［J］.Int J Sport Physiol，2012，7（1）：26－32.

［25］FOSTER C，GREEN M A，SNYDER A C，et al.Physiological responses during simulated competition［J］.Med Sci Sport Exerc，1993，25（7）：877－882.

［26］GARLAND S W.An analysis of the pacing strategy adopted by elite competitors in 2000mrowing［J］.Brit J Sport Med，2005，39（1）：39－42.

［27］MARCH DANIEL S，VANDERBURGH PAUL M，TITLEBAUM PETER J.Age，sex，and finish time as determinants of pacing in the marathon［J］.J Strength Cond Res，2011，25（2）：386－391.

［28］SANDALS L E，WOOD D M，DRAPER S B，et al.Influence of pacing strategy on oxygen uptake during treadmill middle－distance running［J］.Int J Sports Med，2006，27（1）37－42.

［29］THOMPSON K G，HALJAND R，MACLAREN D P.An analysis of selected kinematic variables in national and elite male and female 100mand 200mbreaststroke swimmers［J］.J Sport Sci，2000，18（6）：421－431.

［30］TUCKER R.The anticipatory regulation of performance：the physiological basis for pacing strategies and the development of aperception－based model for exercise performance［J］.Brit J Sport Med，2009，43（6）：392－400.