基于FPGA 的祖冲之算法硬件实现

郭泓键，董秀则，高献伟

(1.西安电子科技大学通信工程学院，西安 710071;2.北京电子科技学院，北京 100070)

1 概述

长期演进(Long Term Evolution，LTE)于2010 年底被指定为第4 代移动通信标准，其中安全技术是LTE 的关键技术［1］。祖冲之(ZUC)算法是LTE 加密算法128-EEA3 和完整性算法128-EIA3 的核心，在2011 年被3GPP LTE 采纳为第4 代移动通信国际加密标准，是第一个我国自主研究设计并成为国际密码标准的密码算法［2］。

ZUC 算法是一种流密码，和分组密码相比，具有加解密速度快、适合硬件实现等特点［3］。随着集成电路技术的高速发展，硬件电路实现加密算法与传统软件加密方法相比具有安全性好、计算速度快、成本低、性能可靠等优点［4］。现场可编程门阵列(Field Programmable Gate Array，FPGA)器件因其现场可编程和低成本等特性在密码算法实现领域有着突出的优势［5］。因此，基于FPGA 器件实现ZUC 算法具有一定的现实意义。

目前，已有多篇文献对ZUC 算法的FPGA 实现进行了研究。但大都不能同时兼顾高吞吐量和低资源占用。例如文献［6］提出的方法逻辑资源占用为385 个slice，但是只达到了2.08 Gb/s 的吞吐量。文献［7］提出复用S 盒和CSA 树的设计方法，在分别占用311 个slice 和356 个slice 的情况下只达到2.0 Gb/s和3.456 Gb/s 的吞吐量。文献［8］提出的方法在CSA 树结构的基础上进行了改进，在占用395 个slice 的情况下达到5.504 Gb/s 的吞吐量。文献［3］采用流水线的设计方法仅对ZUC1.4 版本的工作阶段进行了实现，其实现的内容相比现在的ZUC 1.6 版本完整算法要简单很多，参考价值不大。本文提出了一种新的方法，通过使用占用逻辑资源较少的简单加法器完成了复杂的mod(231-1)加法运算，在仅占用305 个slice 的情况下达到了5.647 Gb/s的吞吐量。

2 ZUC 算法简介与实现分析

ZUC 算法是一种面向字的流密码，输入为一个128 bit 的初始密钥k 和一个128 bit 的初始矢量iv，输出为32 bit 的密钥流［9］。其整体结构如图1 所示，共包含3 个逻辑层，由上到下分别是线性反馈移位寄存器(LFSR)、比特重组(BR)和非线性函数F。

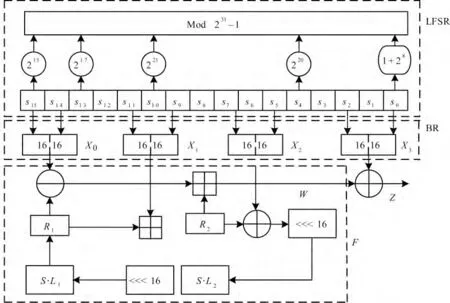
图1 ZUC 算法整体结构

2.1 ZUC 算法

ZUC 算法的执行分为2 个阶段:初始化阶段以及工作阶段。

2.1.1 初始化阶段

首先，密钥加载过程把128 bit 的初始密钥k=k0‖k1‖…‖k15，128 bit 的初始向量iv=iv0‖iv1‖…‖iv15以及240 bit 的长字符串D=d0‖d1‖…‖d15以si=ki‖di‖ivi(0≤i≤15)的方式加载到LFSR 的16个存储单元si(0 ≤i≤15)中。其中，ki和ivi均为8 bit，di为15 bit，si定义在素数域GF(231-1)上。然后，将32 bit 记忆单元R1和R2清零。最后，依次执行BR、非线性函数F、LFSR 初始化模式3 个步骤，重复执行32 次。

BR 的具体操作为:X0=s15H‖s14L，X1=s11L‖s9H，X2=s7L‖s5H，X3=s2L‖s0H，siH和siL分别是si的高位16 bit 和低位16 bit。

非线性函数F 依次执行以下计算:W=(X0⊕R1)R2，W1=R1X1，W2=R2⊕X2，R1=S(L1(W1L‖W2H))，R2=S(L2(W2L‖W1H))。S 是32 × 32 的S 盒。

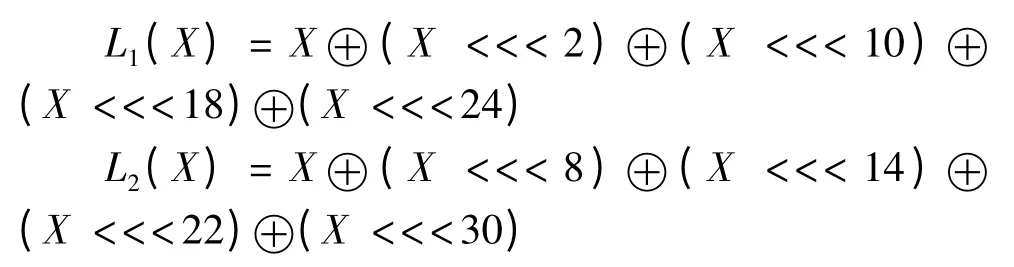
LFSR 初始化模式的具体操作为:

(1)v=215s15+217s13+221s10+220s4+(1 +28)s0mod(231-1)。

(2)s16=(v +u)mod(231-1)，其中，u 为非线性函数F 的输出W 去掉最右端比特位。

(3)如果s16=0，那么设置s16=231-1。

(4)(S1，S2，…，S16)→(S0，S1，…，S15)。

2.1.2 工作阶段

首先，顺序执行BR、非线性函数F(丢弃非线性函数F 的输出W)、LFSR 工作模式3 个步骤一次。然后，按顺序迭代执行BR、非线性函数F、Z=W⊕X3、LFSR 工作模式，每执行一次得到一个32 bit 的字Z。其中，LFSR 工作模式的具体操作为:

(1)s16=215s15+217s13+221s10+220s4+(1 +28)s0mod(231-1)。

(2)如果s16=0，那么设置s16=231-1。

(3)(S1，S2，…，S16)→(S0，S1，…，S15)。

2.2 ZUC 算法实现分析

ZUC 算法BR 逻辑层和非线性函数F 逻辑层中涉及到的运算包括模232加法、S 盒变换、字符串的级联、异或和循环移位。其中，2 个32 bit 数据进行模232加法运算在VHDL 语言中可以直接利用运算符“+”完成，S 盒变换可以通过查表(LUT)的方式快速实现。字符串的级联、异或和循环移位这3 种运算都是对数据比特位顺序的改变或者是对数据比特位的简单运算，在硬件上都比较容易实现。

ZUC 算法LFSR 逻辑层中涉及到的运算主要包括素数域GF(231-1)上31 bit 的字符s 与2i(i=15，17，21，20，8)相乘，以及31 bit 数据mod(231-1)加法运算。231-1 是一个特殊的大素数［10］，其二进制形式是31 bit 1，可以看出素数域GF(231-1)上31 bit 的字符s 乘2i(i=15，17，21，20，8)可以通过数据s 向左循环移位i 位快速实现。由此得到LFSR 中215s15，217s13，221s10，220s4，28s0可以分别如下快速实现:s15＜＜＜15，s13＜＜＜17，s10＜＜＜21，s4＜＜＜20，s0＜＜＜8。

但是在硬件上实现多个31 bit 数据mod(231-1)相加是相对复杂的，已公开发表的论文都是通过使用多个较复杂的加法器来实现。ZUC 算法执行过程中mod(231-1)加法运算需要被执行多次(ZUC算法初始化阶段，LFSR 初始化模式需要被执行32 次，每次需要执行7 次mod(231-1)加法运算;ZUC 算法工作阶段，LFSR 工作模式需要被执行多次，每次需要执行6 次mod(231-1)加法运算)，因此，LFSR 逻辑层中方程式(1)、方程式(2)的实现需要消耗较多的硬件资源，会产生较多的延时。

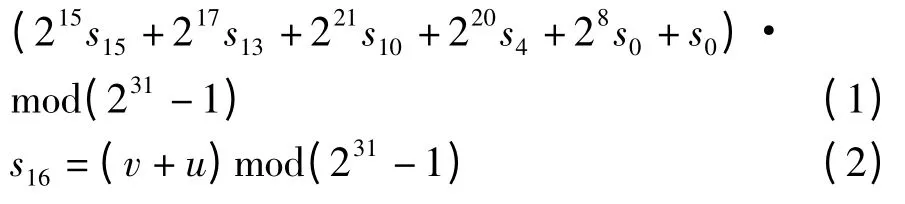
3 ZUC 算法的实现

根据ZUC 算法的特点，将ZUC 算法的整体结构分为库函数模块和主程序模块。主程序实体硬件接口如图2 所示。各管脚定义硬件接口设计为同步接口，每一个输入输出信号都在时钟周期的上升沿采样。

通过2.2 节的分析可知，LFSR 中式(1)、式(2)的实现消耗时间最长，需要资源最多，是基于FPGA实现ZUC 算法的关键路径。已公开发表的论文通过使用多个较复杂的加法器来实现这一关键路径，其资源使用情况大致如表1 所示。

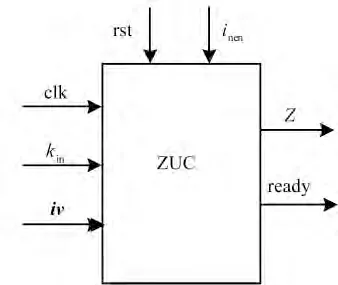
图2 主程序实体接口

表1 ZUC 算法关键路径资源使用

mod(231-1)加法器由2 个32 bit 加法器和1 个选通器(MUX)组成，如图3 所示。而进位保留加法器(CSA)较mod(231-1)加法器会占用更多的资源［11］。

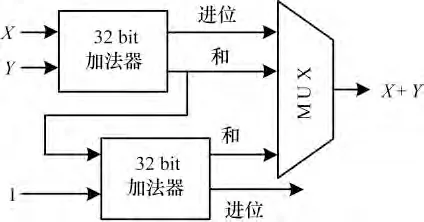
图3 mod(231 -1)加法器

为了进一步减少硬件资源占用，提高吞吐率，本文提出了一种新的实现方法。mod(231-1)加法是在素数域GF(231-1)上进行的，231-1 是一个特殊的素数，其二进制形式为31 bit 1。如果方程式(1)中6 个数据相加的和小于231-1，则其模231-1 是它自身。6 个31 bit 数据相加最大可产生1 个34 bit数据，所以如果表(1)中6 个数据相加的和大于231-1，那么其二进制形式位数一定大于等于32 位，小于等于34 位。若其从右至左第32 bit 为1，也就是十进制数231，231模231-1 后恰好为二进制数1;若其从右至左第33 bit 为1，也就是十进制数232，232模231-1 后恰好为二进制数10;若其从右至左第34 bit为1，也就是十进制数233，233模231-1 后恰好为二进制数100。可以看出如果方程式(1)中6 个数据相加的和大于231-1，其二进制形式每个从右至左第(31 +n)位为1 的比特位都会在其模231-1 后产生一个从右至左第n bit 为1 的二进制数。综上可以看出，mod(231-1)加法可以使用简单的加法器和移位操作来实现。

考虑到方程式(1)、方程式(2)中运算的迭代特点和很好的并行特性，为了在算法实现面积和速度方面取得平衡，本文根据上述结论采用混合方式对关键路径对应的方程式(1)、方程式(2)进行了实现，具体流程为:

(1)在方程式(1)中6 个31 bit 数据最高位前分别补3 bit 0，使其变为6 个34 bit 的数据，分别记为A，B，C，D，E，F。

(2)使用1 个34 bit 加法器迭代计算A，B，C 三者之和，结果记为G。同时并行使用另一个34 bit 加法器迭代计算D，E，F 之和，结果记为H。

(3)使用第2 个34 bit 加法器计算G，H 之和，记为I。

(4)使用1 个32 bit 加法器将I 的最高3 bit，和剩余31 bit 分别作为2 个二进制数相加，结果记为J(考虑到J 可能会大于231-1)。

(5)使用1 个31 bit 加法器将32 bit 数J 的最高位1 bit 与剩余31 bit 相加(结果不可能大于231-1)，结果即为方程(1)中的v。

(6)使用上述32 bit 加法器计算方程(2)中两数据之和，记为K。

(7)使用上述31 bit 加法器将K 的最高位1 bit与剩余31 bit 相加，结果即为s16。

本文方法无需判断s16的计算结果是否为0，因此，可以省去1 个选通器(MUX)。这是因为LFSR的所有寄存器单元si(0≤i≤15)的初始值都不为0，故本文方法中数据相加结果不可能为0。

本文提出的方法实现方程式(1)的计算只使用了2 个34 bit 加法器，1 个32 bit 加法器和1 个31 bit加法器，资源占用较其他方法中使用多个CSA 和mod(231-1)加法器相比会大幅减少，同时硬件延时也会大大减少。

4 仿真验证和性能分析

本文利用硬件描述语言VHDL 对ZUC 算法进行了编程实现，在Quartus Ⅱ9.0 上进行了综合仿真。对于初始向量为84319aa8de6915ca1f6bda6bfbd 8c766，初始密钥为3d4c4be96a82fdaeb58f641db17b 455b 的输入，得到了输出14f1c272，3279c419 等数据。结果与文献［12］中测试文件保持一致，证明了本设计的正确性。仿真结果如图4 所示。

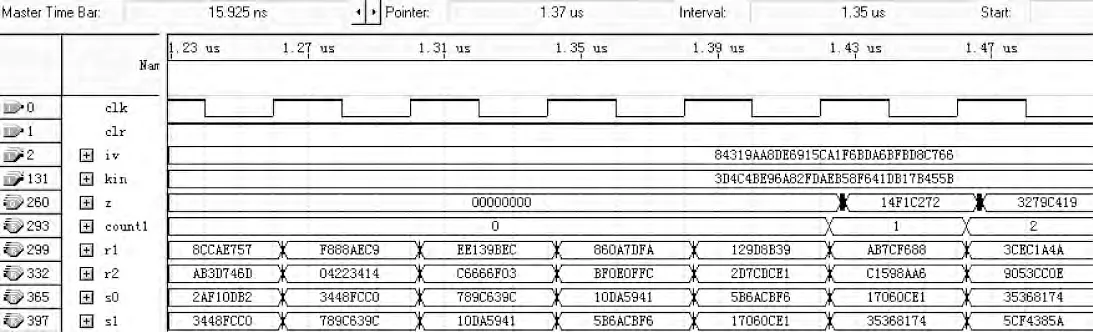
图4 编程实现综合仿真结果

目前业界评估密码算法硬件实现的关键指标主要有吞吐率和芯片面积。为了与其他实现方法进行对比，本文采用XILINX 公司的Virtex5XC5VLX110T 芯片，使用ISE 软件对本文方法进行了综合实现，在仅占用305 个slice 的情况下达到了5.322 Gb/s 的吞吐量。本文方法与其他方法的吞吐率与芯片面积等指标如表2 所示。

本文采用了FPGA 逻辑资源Slice 作为比较的基础，通过对比可以看出，本文方法硬件资源占用最少，仅为305 个slice。而在吞吐率方面，除了文献［8］的方法达到了最高。文献［2］中的方法是对ZUC1.4版本的实现，其余方法都是对ZUC1.6 版本的实现。ZUC1.4 版本是通过方程s16=v⊕u 计算得到s16的，计算量要比ZUC1.6 小很多，而且其初始化部分是在软件中实现的，所以大大减少了延时和硬件资源占用，不具有可比性。本文方法在吞吐量/面积方面达到了最高，较文献［8］方法提高了25.9%。这充分说明，本文方法通过对ZUC 算法关键路径的优化实现，在大幅减少硬件资源消耗的同时保证了极高的吞吐率。

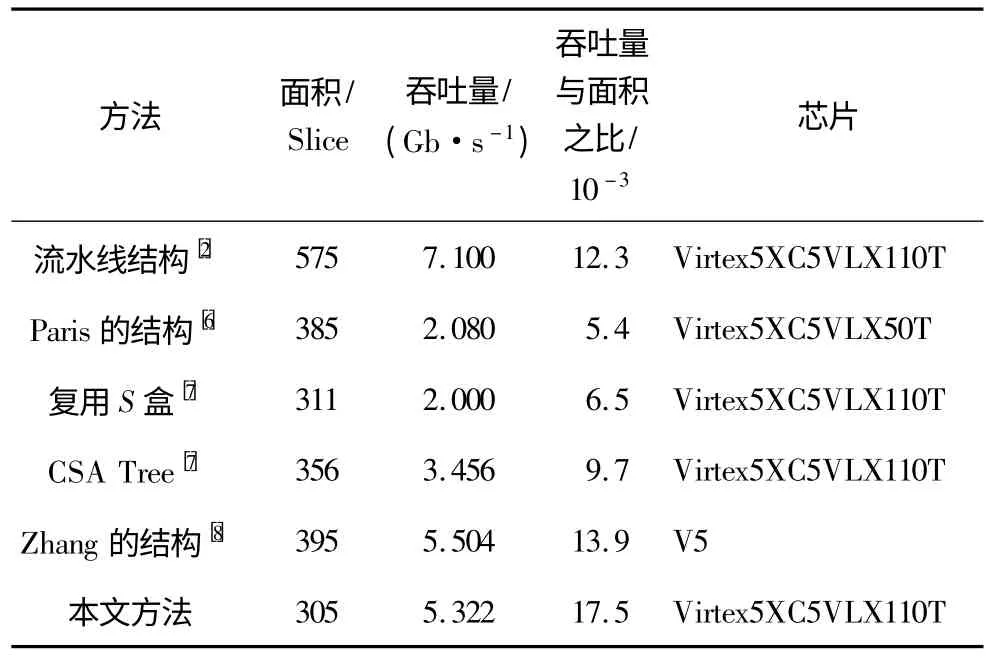
表2 本文方法与其他方法的数据比较

5 结束语

本文在FPGA 平台上设计并实现了一种新的ZUC 算法实现方法，在保证较高吞吐率的前提下，与目前最优实现方法相比，芯片资源占用减少了近23%，单位面积的吞吐量提高了25.9%，具有一定的实际价值。但是本文方法的吞吐量还有待进一步提高，这也是下一步的研究方向。

［1］江丽娜，高 能，马 原，等.祖冲之序列密码算法IP核的设计与实现［J］.信息网络安全，2012，(8):219-222.

［2］冯秀涛.3GPP LTE 国际加密标准ZUC 算法［J］.信息安全与通信保密，2011，9(12):45-46.

［3］Liu Zongbin，Zhang Lingchen，Jing Jiwu，et al.Efficient Pipelined Stream Cipher ZUC Algorithm in FPGA［C］//Proc.of the 1st International Workshop on ZUC Algorithm.Beijing，China:［s.n.］，2010.

［4］Zhang Xinmiao，Parhi K.High-speed VLSI Architectures for the AES algorithm［J］.IEEE Transactions on Very Large Scale Integration Systems，2004，12(9):957-967.

［5］Galanis M D，Kitsos P.Comparison of the Hardware Architectures and FPGA Implementations of Stream Ciphers［C］//Proc.of the 11th IEEE International Conference on Electronics，Circuits and Systems.Tel-Aviv，Israel:［s.n.］，2004:571-574.

［6］Kitsos P，Sklavos N，Skodras A N.An FPGA Implementation of the ZUC Stream Cipher［C］//Proc.of the 14th Euromicro Conference on Digital System Design.［S.l.］:IEEE Press，2011:814-817.

［7］Wang Lei，Jing Jiwu，Liu Zongbin，et al.Evaluating Optimized Implementations of Stream Cipher ZUC Algorithm on FPGA［C］//Proc.of 13th International Conference on Information，Communication and Signal Processing.Beijing，China:［s.n.］，2011:202-215.

［8］Zhang Lingchen，Xia Luning，Liu Zongbin，et al.Evaluating the Optimized Implementation of SNOW 3G and ZUC on FPGA ［C］//Proc.of the 11th IEEE International Conference on Trust，Security and Privacy in Computing and Communications.Liverpool，UK:［s.n.］，2012:436-442.

［9］ESTI/SAGE Specification of the 3GPP Confidentiality and Integrity Algorithms 128-EEA3 ＆ 128-EIA3 Document 2:ZUC Specification［Z］.2011.

［10］ESTI/SAGE Specification of the 3GPP Confidentiality and Integrity Algorithms 128-EEA3 ＆ 128-EIA3 Document 4:Design and Evaluation Report［Z］.2011.

［11］Murugeswari S.An Area Efficient and Low Power Multiplier Using Modified Carry Save Adder for Parallel Multipliers［C］//Proc.of the 2nd International Joint Conference.Bangalore，India:［s.n.］，2012.

［12］ESTI/SAGE Specification of the 3GPP Confidentiality and Integrity Algorithms 128-EEA3 ＆ 128-EIA3 Document 3:Implementor's Test Data［Z］.2011.