混沌特性与气象因素在负荷分类预测中的应用

魏 东彭 格魏 林

1.重庆电力公司电力科学研究院 重庆 401123；

2.重庆科技检测中心 重庆 401147；

3.重庆电力公司南岸供电局 重庆 400060

0 引言

电网负荷短期预测（short time load forecasting，STLF）对于制定电力调度计划、优化发电机组出力和电力公司经济利益的提高具有重要意义，也是大力实施需求响应项目的基础。

传统的预测模型主要有动力学模型和数理统计模型等［1-2］，动力学模型是先建立模型，然后对这些模型进行线性简化，数值求解，从而达到预测的目的。但是一般系统运动过程本身是错综复杂的，对其物理机制难以进行充分了解，而数理统计模型对历史数据要求较高。混沌理论（chaos theory）和相空间重构理论 （phase space reconstruction theory，PSRT）为电力系统STLF的研究找到了新方法。文献［2-4］采用混沌理论模型预测电力负荷，精度要高于其他预测方法。但是基于PSRT的各种STLF模型研究表明，这些模型在气象因素波动较小的时段节表现出很高的预测稳定性和较高的预测精度［5］，但在气象因素变化敏感的时段尤其是夏季高温区预测精度很不理想，主要是因为气象因素增加了负荷的随机波动性。目前，STLF的建模方法主要有两种：一是将所有负荷综合统一建模；二是对内、外部负荷分量分别建模［6］。文献［7］采用统一建模的方法，这会导致主要的混沌动力学行为无法体现，同样也会失去相空间内跟踪演化轨迹的能力，因此对内、外部负荷分量分别建模对提高预测精度具有实际意义。

本文将负荷问题的研究分割进行，在以上基础上采取分类预测方法，建立基本负荷份量预测（basic load component forecasting，BLCF） 模型和与气像相关的随机负荷预测 （meteorology load component forecasting，MLCF）模型，最终形成负荷整体预测。

1 总体负荷预测流程图

基于BLCF和MLCF的预测模型总体流程图如图1。需要说明的是本文的基本负荷分量与气象敏感负荷分量是典型气象日负荷减去非气象日负荷的基础上得来的。

图1 BLCF和MLCF模型预测流程图

BLCF的理论是混沌动力学［8-9］，混沌预测的关键是相空间重构，即如何正确选取延迟时间和嵌入维数，保证时间序列在高维空间把吸引子轨道显示出来，在重构的Rn空间里的轨线上与原动力学系统微分同胚。MLCF关键是如何准确考虑气象因素的影响和精确分类。

2 基本负荷分量预测

2.1 重构相空间

混沌预测的关键步骤是相空间的重构，即延迟时间ζ与嵌入维数m的选取，该参数对时间序列能否在高维空间还原出吸引子轨道至关重要。本文对延迟时间的选取采用自相关法，自相关法是应用较为广泛，比较成熟的方法，主要是通过求取时间序列的自相关性，求得延迟时间。一般情况下，当自相关函数下降到 1－1／e（0.632）时，对应的是最佳延迟时间ζ。对某地区的基本负荷分量时间序列做出自相关函数图，进行延迟时间求取，如图2所示。从图2中可见，当自相关系数下降到0.632时，对应的延迟时间为5。

图2 自相关法求延迟时间

根据嵌入定理，只要嵌入维数m>2d+1即可在高维空间中揭示混沌吸引子，郝柏林认为如果涉及到Lyapunov指数或维数等沿轨道的某种平均统计量，则只要满足2d>m>d。在实际的电力负荷预测中嵌入维数不能过大，否则会降低有效数据量，过小无法揭示时间序列的混沌特性。目前确定嵌入维数的方法有伪最邻近点法，Cao氏方法，C-C方法、G-P算法。G-P算法是计算关联维数的一种，可以有效的反应吸引子的不均匀性和动态特性，得到了广泛的应用。图3、图4为应用G-P算法得到的仿真图。

图3 关联积分指数变化

图3中横坐标表示的是负荷序列关联积分指数，纵坐标表示的是欧式距离极限指数，图4中表示的是嵌入维数与吸引子关联维数的关系。从图3、图4中看出m=8以后关联维数已趋于饱和，对应的吸引子维数d=2.12，此时的关联维数为相空间重构的最佳嵌入维数。

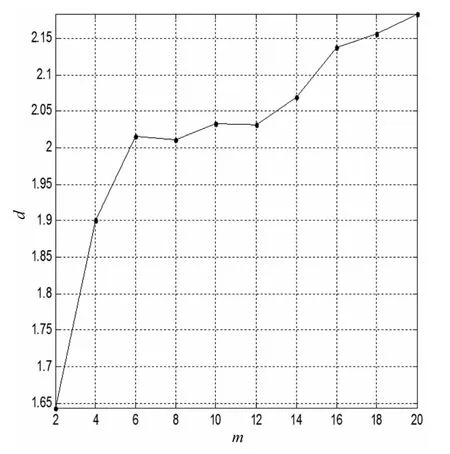
图4 关联维数m变化趋势

2.2 混沌动力学预测

混沌动力学预测方法主要有全域法、局域法、加权零阶局域法、加权一阶局域法，加权一阶局域法通过实际应用和数值试验相比其他几种预测方法具有更高的预测精度。根据上述得到的延时时间与嵌入维数重构相空间，选取加权一阶局域法预测，预测结果如下图5：

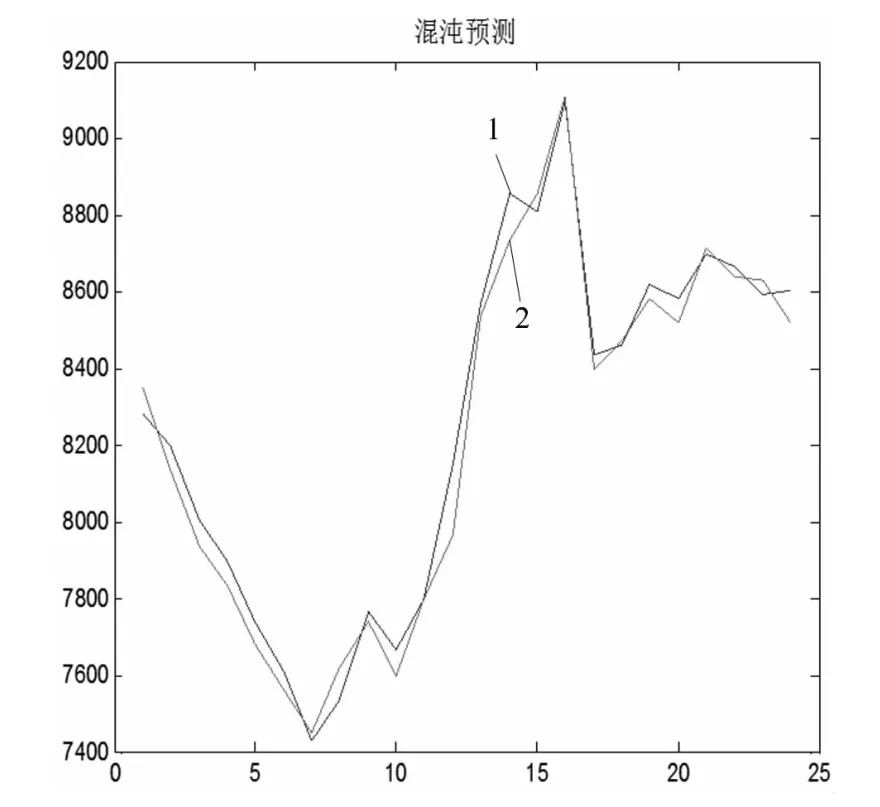
图5 混沌负荷预测

图5中1为实际负荷，2为预测负荷，从图中可见，预测结果与实际值之间的误差控制在2.34%以内，两曲线拟合度为0.96，标准差为4.32，与其他传统方法相比具有较高的预测精度。

3 气象负荷预测

气象因素对电网负荷波动的影响越来越大，尤其是夏季高温造成的负荷波动，这给负荷预测造成了很大困难。影响夏季负荷波动的影响因素主要有温度、湿度、降水量、风等，本文引入人体舒适度概念［10］来对上述因素统一考虑，对气象敏感负荷进行聚类分析，把具有相同人体舒适度和负荷特性的负荷聚类在一起，形成负荷特性识别表，当需要进行负荷预测时调用上述表中的负荷数据作为BP神经网络的输入进行预测，避免了相关性不强的数据输入，造成预测结果的偏差。

3.1 人体舒适度

人体对外界的感觉是受多种因素的复杂影响，包括温度、湿度、风速、雨水等，各个因素的影响程度又不相同。温度是其中最重要的因素，夏季人体最适宜的温度在19~24度，冬季在19~22度，当温度超出此范围时，人们能便会采取措施降温或取暖，造成负荷波动。湿度对人体感觉具有较弱的正相关性。当气温为32度时，风速大于4m/s，人体不会感到热，而在没有风时，人体就会感觉热，风速没加强1m/s，人体感觉气温下降2度左右。为此本文采用人体舒适度的概念来表征各种主要因素的影响，按照公式（1）进行划分。

其 中 C2=0.44C5+0.42C6，C1，C2，C3，C4，C5，C6分别表示气压，晴朗、温湿、风冷、日照、降水指数。根据公式（1）把夏季高温阶段划分为4个等级，如表1所示，基本可以表征人体对各种气象因素的反应。

表1 夏季人体舒适度等级表

3.2 聚类分析

对于分类数目不能太多，易造成相似特征的负荷数据分割为不同的类，又不能太少，致使没有相似特征的负荷分为一类，导致预测结果不准确。分类方法上多采用单步分类［11］，本文采用系统-模糊C均值两步聚类法，避免了系统聚类效果不理想和模糊C均值对初始聚类的敏感性。按照舒适度等级把夏季高温阶段分为 4 类，如图 6（a）、（b）、（c）、（d）所示。

第1类气象负荷在0点到10点之间较小，10点之后气象负荷快速增加达到650kW，人体舒适度下降，表征的是人体舒适度中的第3级。第2类气象负荷波动最大达到800kW，表征人体舒适度中的第2级，气象负荷有所凸显。第3类负荷在15点以后增加，之后最高达到550kW左右，气象负荷出现时间较前两种都短，属于人体舒适度第四级。第4类负荷波动平稳，基本在600-650kW左右，说明此时的天气状况已经非常炎热，需要持续采取措施，保证人体舒适度，属于人体舒适度的第1级。

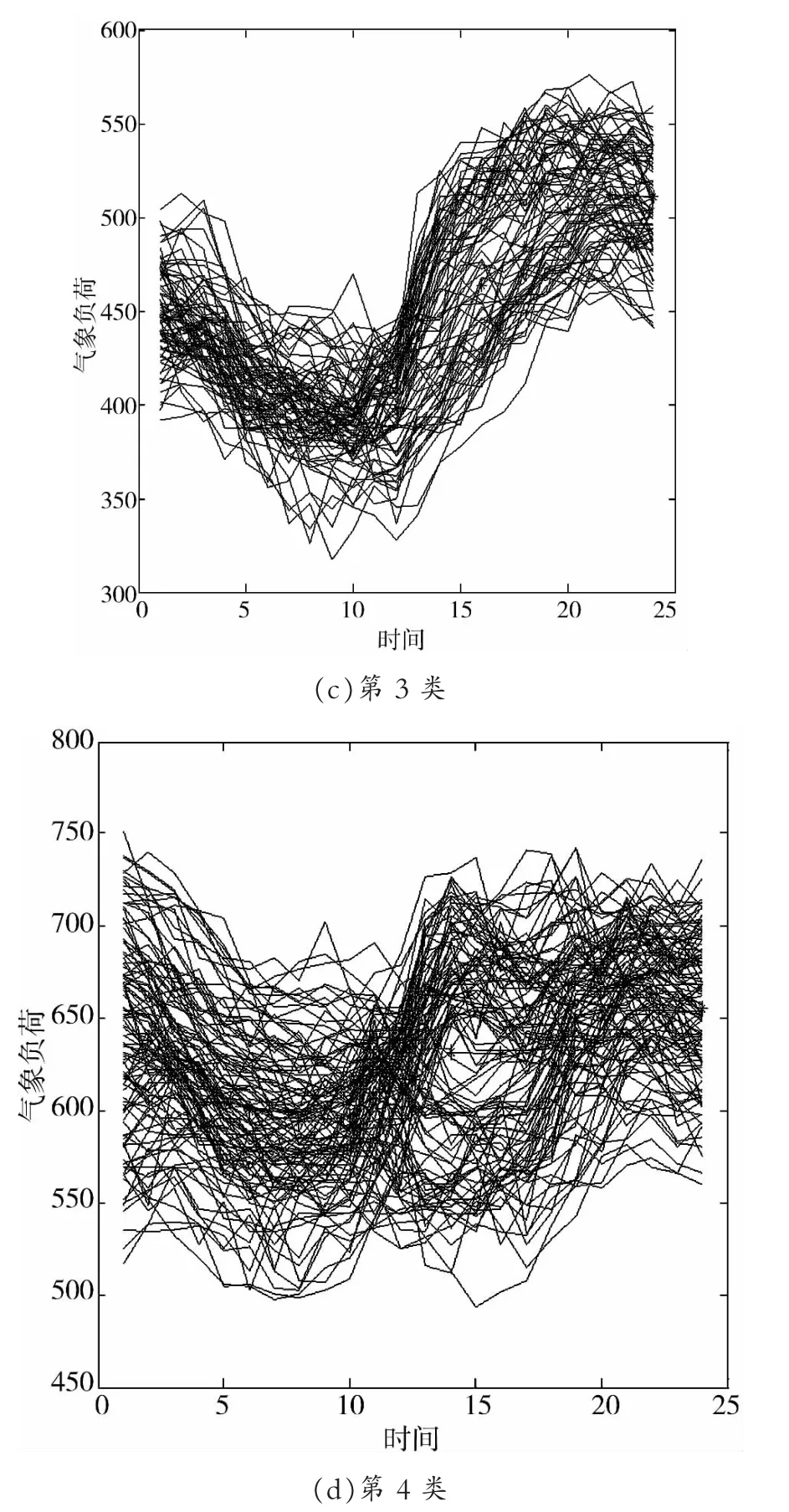
图6 按舒适度气象负荷分类图

3.3 气象负荷预测

对气象负荷预测采用BP神经网络，BP神经网络是一种按误差逆传播算法训练的多层前馈网络，具有强大的非线性映射能力，较强的容错能力和对噪声的鲁棒性，得到了广泛应用，具体理论不再叙述。数据根据次日气象条件确定哪一类为输入数据，仿真结果如图7所示。

图7 神经网络预测

图7中1线为预测日的实际负荷，2线为预测负荷。最大误差为3.8%，两曲线拟合度为0.92，标准差为6.58，具有较好的预测能力。

4 结论

本文通过对电力负荷采用分类预测，即具有混沌动力学特征的BLCF和气象因素引起的MLCF。BCLF采用混沌理论预测，首先根据自相关法和G-P算法确定延迟时间、嵌入维数，保证在高维空间充分显示吸引子轨道，进而运用加权一阶法预测，结果表明预测误差在2.34%以下。MLCF通过引入人体舒适度指数表征各种气象因素对负荷波动的影响，把夏季高温阶段分为4个舒适度等级，采用系统-模糊C均值两步聚类，提高聚类效果，把相应聚类类别作为BP神经网络的输入，算例分析表明预测误差在3.8%以下，具有良好的预测精度。提出的分类预测模型对准确预测短期电网负荷具有重要参考意义。

［1］钟庆，吴捷，伍力，黄武忠.基于系统动力学的分区预测［J］.电网技术，2001，25（3）：52-54.

［2］陈春琴.数理统计分析在电力企业负荷预测中的应用［J］.华东电力，2006，34（5）：55-58.

［3］张智晨，孙雅明，张世英.基于负荷内部特性和外部随机因素的短期负荷预测模型 ［J］. 电网技术，2006，30（8）71-74.

［4］周金勇.混沌时间序列模型研究［D］.武汉：武汉理工大学，2009.

［5］孙雅明，张智最.相空间重构和混沌神经网络融合的短期负荷预测研究［J］.中国电机工程学报，2004，24（1）：44-48.

［6］冯丽，邱家驹.基于电力负荷模式分类的短期电力负荷预测［J］.电网技术，2005，29（4）：23-26，40.

［7］ Drezga I，Rahman5.Input variable selection for ANN-based short time Ioad forecasting ［J］.IEEE Trans on Power systems，1998，13（4）：1238-1244.

［8］蒋传文，袁志强，侯志俭，等.高嵌入维混沌负荷序列预测方法研究［J］.电网技术，2004，28（3）：25-28.

［9］田聪.基于混沌理论的电力负荷短期预测［D］.哈尔滨：哈尔滨理工大学，2007，18-20.

［10］毛新桦.基于人体舒适度指数负荷特性分析方法的研究［D］.南京：东南大学，49-55.

［11］张智最，孙雅明，张世英，等.基于数据挖掘多层次细节分解的负荷序列聚类算法［J］.电网技术，2006，30（2）：51-56.