研究设计中样本量的确定

鲍 贵

(南京工业大学 英语系，江苏 南京 211816)

1.引言

任何推理统计都涉及到两类错误率，即第一类错误率(Type I error rate，记作α)和第二类错误率(Type II error rate，记作β)。第一类错误率是零假设(H0)为真却被错误拒绝的概率，因而不拒绝零假设的置信度为1－α。第二类错误率是零假设为误却被错误接受的概率，因而拒绝零假设的置信度为1－β。以往的研究重视第一类错误率，将α值设得很低，譬如.05或.01等，以期获得科学的新发现。传统上对第二类错误率的重视程度不足，主要是因为研究者通常希望证实与零假设相对立的备择假设(Ha，又称研究假设)而非零假设本身，零假设的提出与拒绝只是为备择假设的成立提供反证。

实际上，第一类和第二类错误率是紧密联系的，重视一类错误、忽略另一类错误不是很好的统计思维方法。近40年来，尤其在 Cohen(1969;1977;1988)的力作问世之后，研究者们逐渐意识到第二类错误率和第一类错误率一样值得重视，因为它们均对能否得到科学的新发现起着至关重要的作用。不过，研究者们在研究第二类错误率时却通常换用其补数(1－β)，将之称作统计效力(statistical power，简称效力)，以此反映零假设为误时研究拒绝零假设的能力。在科学的实证研究中，由于并不真正知道会犯哪类错误，因而研究者既需要控制第一类错误率，以避免在零假设为真的情况下得到虚假的研究发现，又需要控制第二类错误率(即提高统计效力)，以便在研究假设为真的情况下能够得到研究发现。关于实证研究中效力的重要性，Hallahan＆Rosenthal(1996:491)做了很好的概括:(1)如果计划研究时不考虑效力，研究能够发现实际存在的效应的可能性或许很小。其结果是，由于不可能拒绝零假设而造成时间和资源的浪费。(2)由于解释结果时没有考虑效力，研究者可能将无显著性结果解释为零假设为真，从而过早地放弃很有前景的研究取向。Shadish等.(2002)和 Heppner等(2008)等将低统计效力视作统计结论效度的重要威胁。美国心理学会(American Psychological As-sociation，2010:30)建议，使用推理统计时，研究者应考虑与假设检验相关的统计效力。这关系到在α水平、一定效应量(effect size，简称ES)和样本量(sample size)条件下正确拒绝所要检验的假设的可能性，因此，研究者应常规性地提供证据，表明研究有足够效力发现有实质性意义的效应。

在研究设计中，要保证统计效力，就要考虑选用合适的样本量。外语教学研究者在研究设计中通常对选择多大的样本量没有把握，样本量选择过大或过小的情况时常出现。样本量选择过大虽然不会削弱统计效力，但是往往会造成人力和物力资源的浪费，使研究设计显得不经济。而且，样本量过大也更易产生统计显著性结果(即概率p＜α)，可能导致研究发现没有实际意义的效应量。当然，习惯于直接解释效应量的研究者不会落入根据p值判断效应是否重要这一陷阱(Ellis，2010:52)。另一方面，样本量过小则会使统计效力降低，减少了发现总体效应的可能性，不仅造成人力和物力资源的浪费，还会导致错误的结论，譬如将统计不显著的结果错误地解释为接受零假设。因此，样本量过大和过小都会降低研究的效率。优化研究设计必须考虑效力、效应量和样本量之间的关系，选择适当的样本量。本研究以方差分析(含t检验)为例介绍统计效力和效应量的基本概念，分析样本量与其他影响参数之间的关系，为样本量的确定提供必要的方法。

2.决定研究所需样本量的参数及其相互关系

2.1 样本量、第一类错误率、效力和非中心参数

就方差分析而言，传统上影响效力的参数为第一类错误率、样本量和非中心参数(noncentrality parameter，简称NCP，记作λ)。非中心参数表示研究假设偏离零假设的程度，计算公式为:

公式中，SSHa是研究假设中期望平均数的平方和，n是每个比较总体平均数μi的样本量，μ是各个比较总体平均数μi的平均数，k是比较总体数。σ2是总体方差，常用方差分析中的误差均方(MSE)来估计。零假设为真时，λ =0，F分布为中心分布。研究假设为真时，λ≠0，F分布为非中心分布。自由度确定时，零假设条件下的F分布只有一个，即中心F分布，但是同样自由度时的非中心F分布却有多个，分布的位置取决于λ。非中心参数λ值越大，非中心F分布就越远离中心分布，统计效力就越高。图1显示单因素方差分析时中心和非中心F分布中各个参数之间的关系。

图1 中心与非中心F分布比较

左图中心F分布F(k－1，k(n－1))临界值右边的面积等于α值。右图中的β值为非中心F分布中小于或等于α值所对应的F临界值的F统计量的概率，效力为1－β。中心F分布临界值是F分布的分子、分母的自由度和α的函数，其中，分子、分母的自由度完全由比较总体数k和每组样本量n决定。中心F分布的临界值越大，临界线就越向右移，β值就会越大，效力也就越低，反之亦然。α值不变时，对于比较组数(k)相同的方差分析，每组样本量(n)越大，F分布临界值就越小(图中的临界线左移)，β值随之减小，效力也就增加。如果α值也增加，F分布临界值就会更小，β值也会更小，效力也就会再增加。

下面仍以单因素方差分析为例探讨不同参数之间的关系。假设三个比较总体的平均数分别为μ1=85、μ2=90 和 μ3=80，标准差 σ =10。我们利用R软件(鲍贵，2012)编写程序考察在α =.05、每组样本量n取10－30区间21个不同值时，样本量、非中心参数和效力之间的关系，统计结果见表1。

表1 显示，k=3、n=10 时，效力为 0.46，即在总体效应存在的情况下，基于该样本量发现它的概率却不到50%。要提高效力，就要增加样本量。当每组样本量增至20时，效力水平基本达到0.8。在此之前，效力随样本量增加而增加的速度较快，而在此之后，效力随样本量增加的速度有减缓的趋势，样本量的影响力减小。

总体上，α值不变时，增大任何两个参数值，都会增大第三个参数值。在一个参数值减小的情况下，要使另一个参数值保持不变，就要增大第三个参数值。譬如，如果非中心参数值小，要使效力保持在一个较高的水平，那就需要增加样本量。实际研究中，由于α值通常设定为.05，研究者往往根据n和λ确定效力或根据λ和效力确定研究所需的样本量。

表1 不同参数之间的关系

2.2 样本量、第一类错误率、效力和效应量

从λ的计算公式可以看到，λ不独立于样本量n，即λ不是反映总体特征的一个固定值。这两个参数的相互依赖性往往使得研究者不便依据λ来确定研究所需的样本量。当今研究中，往往用反映总体特征的一个固定参数来替代λ。这一固定参数就是Cohen(1969;1977;1988)提出的独立于样本量的效应量。效应量是指某个现象存在于总体中的程度或零假设错误的程度(Cohen，1988:9－10)，测量上表现为标准化平均数的标准差。方差分析中，效应量(用f表示)的计算公式为:

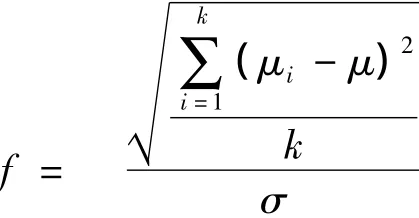
零假设为真时，f=0;零假设为误时，f≠ 0。在n和α值不变时，f值越大，效力就越高，反之亦然。表1的21个样本中，虽然λ值各不相同，但是效应量均相等(f≈0.41)。在f和α值不变时，如果要使效力保持在一个较高的水平，切实可行的办法是增加样本量。

由于f是反映总体平均数差异大小的一个稳定的特征，所以用它来估计研究所需的样本量比使用λ更为方便。以下仍以三组单因素方差分析为例探讨不同参数之间的关系。图2显示单因素方差分析(k=3，α =.05)中效应量与样本量之间的关系随效力变化的趋势。

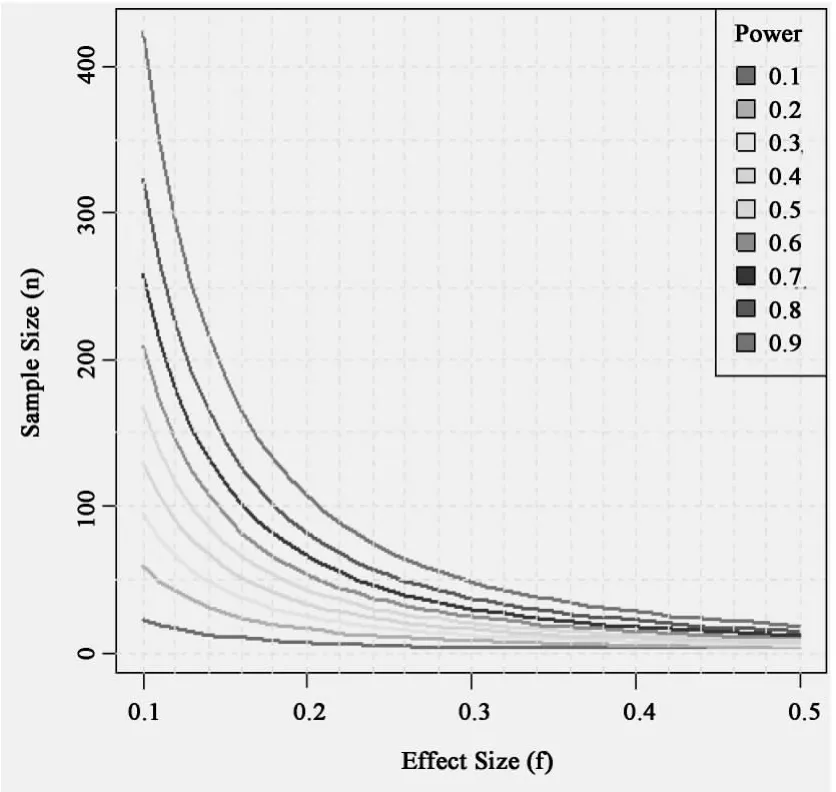
图2 不同效力中效应量与样本量的关系

图2中的9条曲线自下而上反映效力水平为0.1－0.9时研究需要的每组样本量。总体上，效力恒定时，随着效应量的增加，研究所需的样本量呈下降趋势。效应量介于0.1－0.25之间时，图中曲线下降较为陡峭，说明样本量受效力水平的影响较大。效应量大于0.25之后，曲线变化较为平缓，说明样本量受效力水平的影响减弱。效应量大于0.4之后，9条线几乎重合，效力水平对样本量的影响大大减弱。效应量小时，要使研究的效力保持在较高的水平，则必须扩大样本量。如果效应量大，即便要保持较高的效力水平，样本量也不必很大。

表2以具体数值的形式反映单因素方差分析(k=3，α =.05)中每组样本量、效力和效应量之间的关系。

表2 不同效力和效应量条件下的每组样本量

当f值为最小值0.1、每组样本量为22时，效力只有0.1，因而虽然总体效应存在，基于该样本量发现它的概率却只有10%。随着样本量的增大，效力也在增大。如果要达到0.8这一效力水平，每组样本量则应为323。随着效应量的提高，达到同等效力所需的每组样本量则减少。譬如，在效应量为0.3时，要达到效力水平0.8，每组所需样本量降至37。如果效应量高达0.5，每组样本量为14时便可达到效力水平0.8。

3.确定研究所需样本量的方法

3.1 确定α、效力水平和效应量

效力分析涉及四个参数，即样本量(n)、α、效力和效应量(或非中心参数)。知道其中的任何三个参数便可求得另一个参数。效力分析的主要目的之一是在研究设计阶段根据参数之间的关系确定研究所需的样本量。要确定研究所需的样本量，就要确定其他三个参数。为了同时控制第一类和第二类错误率，α和β通常设定为很小的水平。按常规，α =.05、.01或.001，其中 α 最常用值为.05。对于β值设定的规约性没有α那么强，但是当今研究中β的通常值设定为0.1，即效力取值为0.9，0.8常被视作可接受的最小效力值(即 β =0.2)(Batterham ＆ Atkinson，2005:158)。传统上，β 取值大于α之值，反映出研究者对错误接受零假设不那么保守。正如Cohen(1988:56)所说，通常情况下，行为科学家判定第一类错误比第二类错误严重，因此需要更加严防。没有发现比虚假的发现危害程度小这一认识与传统的科学观是一致的。研究者通常固定α和β值，其目的是为了控制基于样本的统计推理可能犯的不同类型错误。因此，研究者最重要的工作就是确定研究总体效应量或非中心参数。由于非中心参数与样本量不独立，因而，比较切合实际的做法是估计总体效应量。一旦明确了总体效应量估计，研究所需的样本量便可确定。总体效应量通常是未知的，准确估计它至关重要，因为它不仅直接影响对研究所需样本量的估计，而且也是科学研究追求的目标。

研究者通常可以用不同方法估计总体效应量。最好的方法是回顾相关实证研究，计算平均效应量作为总体效应量的最接近的估计。如果前期研究没有提供基于样本的效应量，研究者可以根据它们提供的基本数据(比如平均数和标准差)计算估计的效应量。计算平均效应量可采用加权(weight)方法，最简便的方法是以样本量作为权重(Hunter＆Schmidt，2004;Ellis，2010)。利用前期各项研究的效应量估计平均效应量采用加权的方式而不采用简单地求它们的算术平均数(即各个研究效应量之和除以研究的数量)的理由是，来自大样本的效应量估计因为取样误差小，所以比来自小样本的估计更准确，在平均效应量估计中应占有更大的权重。现以实验研究中常用的独立样本t检验为例。该检验用于比较实验组和对照组平均数差异，是单因素方差分析的简化形式。效应量(d)的计算公式为:

公式中，ME和Mc分别代表实验组和控制组总体平均数，σ为每个总体的标准差(假设每个总体的标准差相等)。该公式也适用于非实验条件下两个独立组比较时的效应量计算。如果前期研究对两个独立样本平均数差异采用单因素方差分析，则d=2f。实际研究中，用样本平均数(和)和合并标准差(SD)估计对应总体参数。两组样本量相等时，合并标准差为两个样本方差(VE和VC)平均数的平方根。假定某研究者回顾前期五项研究得到表3数据。

表3 五项研究的结果和效应量

根据d的计算公式，求得各项研究的效应量，如表3最后一列所示。从效应量估计值来看，各研究之间有很大差异。总体效应量的最优估计为各研究效应量加权平均数()，计算公式为:

公式中，wi是权重，di是第i个研究的效应量，k是研究的数量。本研究使用的权重是样本量Ni(第i个研究两个样本量之和)，经计算得到≈ 0.35。

由于d可以有方向性地比较实验组和控制组标准化平均数差异的大小，因而在元分析(metaanalysis)中常采用加权的方法估计总体效应。方差分析是无方向性的。在比较多组(三组或三组以上)平均数差异时，该分析只能回答各组之间有无显著性差异存在，不能明确差异的具体位置，除非进行多重比较(multiple comparisons)。正因为如此，统计学家不对多组方差分析中的效应量f进行元分析。不过，在研究设计阶段，为了确定研究所需的样本量，研究者也可以用以上对d的加权方法估计平均效应量f，作为对总体效应量的最近似估计。如果研究者不采用这一估算方法，也可以只计算出与自身研究相似的前期研究的效应量f，再决定合理的效应量应该有多大。

另一种方法是在没有前期实证研究结果做参考的情况下开展先导研究，对研究总体的效应量进行恰当的估计。第三种方法是结合研究实际合理地主观估计效应量。该方法适用于既没有前期相关实证研究结果作为支撑、条件又不允许开展先导研究的情形。由此得到的总体效应量估计可能不是很精确。最后，如果研究者认为合理的估计很难，不妨采用Cohen(1988)的建议。Cohen(1988)针对各种统计分析方法提出的效应量大小的标准可以作为合理的参照。譬如，Cohen(1988:25－27，284－288)将t检验中小、中、大效应量分别操作定义为d=0.2、d=0.5 和d=0.8;方差分析中的小、中、大效应量分别操作定义为f=0.1、f=0.25和f=0.4。在缺乏判断效应量大小的依据时，建议研究者采用小效应量计算研究所需的样本量，以免效应量估计过高导致实际统计效力降低。不管研究的实际效应量有多大，如果研究有足够的效力确保发现小效应，那么犯第一类或第二类严重错误的风险就会很小(Murphy＆Myors，2004:59)。

3.2 计算研究所需样本量的方法

在设定第一类错误率α和效力水平，并且估计出总体效应量之后，便可以确定研究所需的样本量了。研究所需样本量的确定方法主要有以下几种。第一种是利用R和SAS等软件的外置或附加效力分析程序计算出不同统计分析需要的样本量。譬如，表3中的平均效应量珔d≈0.35，设α=.05，效力水平为0.8。使用R的外置程序pwr，输入命令:pwr.t.test(d=0.35，sig.level=.05，power=.8，type= “two.sample”，alternative= “greater”)，则单侧t检验所需要的每组样本量为102。这意味着，要使研究在80%的情况下能够发现总体效应(0.35)，每组的样本量应为102。如果研究者使用双侧t检验，则只需将命令中的“greater”改为“two.sided”，由此得到n=130，比单侧t检验需要的样本量要大一些。

PASS和G*Power等效力分析专用软件也是很方便的选择。这些软件能够计算各种统计分析的效力或需要的样本量，并能绘制出各种效力分析图形。G*Power是免费使用软件(网址:http://www.psycho.uni－duesseldorf.de/abteilungen/aap/gpower3/download－and－register)，且界面操作简便，因此建议研究者使用该软件。关于该软件各种统计分析功能的详细介绍，研究者可参考Faulet al.(2007)、Mayret al.(2007)和 Lan ＆ Lian(2010)。

第三种方法是查阅效力分析样本量表。以Cohen(1988)提供的不同统计分析(包括t检验、方差分析和相关分析等)样本量表为例。如果研究的某个效应量在表中有显示，则查表比较方便:在某个α水平上，某个效应量所在的列与设定的某个效力水平所在的排交叉得到的数值即为样本量。譬如，d=0.30、α =.05、效力水平为 0.8 时，查表得到单侧独立样本t检验需要的每组样本量n=138。但是，如果研究的效应量d不在表中，则需要采用近似计算的方法得到样本量，计算公式为:

公式中，分子n.10是在某个α和效力水平上d=0.10时所需的样本量，分母中的d为表中没有显示的效应量，常数1是调整所需样本量的经验平均值。根据表3求出的加权平均效应量0.35不在效力分析表中，但是表中提供了单侧独立样本t检验在 α =.05、效力水平为 0.8 时的n.10值(1237)。在α =.05(单侧t检验)时，样本略微更精确的估计可采用常数0.7代替1，经计算得到本例所需的样本量为n≈102。如果采用双侧t检验，α值和效力水平不变，则n.10=1571(表中值)，经计算得到n≈ 130。

关于方差分析样本量表需要做点说明。Cohen(1988)提供的表为单因素方差分析样本量表。表中列出在分子自由度不同，α和效应量f取不同值时不同效力水平对应的样本量。如果研究的效应量f不在表中，则也需要采用近似计算的方法得到样本量，计算公式为:

公式中，分子n.05是在某个α和效力水平上f=0.05时所需的样本量，分母中的f为表中没有显示的效应量，1为调整样本量的常数。前面提到，独立样本t检验是单因素方差分析的简化形式(比较组限于2个)。用方差分析同样可以得到研究所需的样本量。两组比较时，表3求出的效应量d≈0.35等同于f≈0.175。在 α =.05，效力为0.8时，n.05=1571(表中值)，经计算得到n≈ 130，与上面得到的样本量相同。

Cohen(1988:396－403)谈到因素方差分析中在计算某个效力水平上发现主效应和交互效应所需的样本量时如何利用单因素方差分析样本量表的问题。各个效应量单元格样本量(nc)的计算公式为:

公式中，n'数值上等于表中的n，number of cells为单元格总数，u是效应自由度(等于因素水平数－1)，末尾的1是校正单元格样本〗uB=2，fB=0.4;uA×B=2，fA×B=0.25。为了确定各个效应需要的样本量，研究者决定将α和效力水平分别设定为.05和0.8。对于A因素效应，查表得到n=n'=45，利用上面的公式得到nc≈16，那么研究所需的总样本量N应为96。同样方法可以得到:因素B的单元格nc=11，总样本量N为66;交互作用A×B的单元格nc≈27，总样本量N为162。如果研究者要在效力为0.8的水平上发现中等效应的交互作用，则总样本量应为162。由于162是三个效应量所需样本量的最大值，所以使用此样本量能够保证两个主效应的效力水平在0.8以上。用G*Power计算得到的各效应所需总样本量分别为90(A因素)、64(B因素)和 158(A×B交互作用)。由于舍入和计算方法的不同，这些值略低于利用表格计算得到的对应总样本量。在算法上，Cohen(1988)表中的样本量采用近似算法，G*Power采用精确算法。总体上，这两种方法得到的结果基本一致。对于因素设计，Cohen(1988)算法得到的样本量估计偏高(Erdfelderet al.，1996)。

4.结语

统计学是发展迅猛的一门学科。传统的统计分析方法和统计观念不断地被调整，新的统计分析方法不断涌现。既然外语教学研究是以统计分析为主导的，那么外语教学研究者就有必要跟得上统计学发展的步伐，更新研究方法和统计观念。效力分析是外语教学研究必不可少的研究设计与分析环节。其主要目的之一就是为了在规定第一类和第二类错误率的前提下选择适当的样本量，确保总体效应量存在时一项研究在很大程度上能够发现它。

外语教学研究者对研究所需样本量问题的认识不够深刻，对效力分析还比较陌生。鉴于此，本文以单因素方差分析为例，介绍了决定研究所需样本量的三个重要参数，即第一类错误率、效力和效应量(或非中心参数)，探讨了它们之间的关系，详细分析了确定效应量的方法以及计算研究所需样本量的多种途径，以期引起研究者对确定样本量问题的重视，并在未来研究设计中能够确定恰当的样本量，提高统计分析的水平。

［1］ American Psychological Association.Publication Manual of the American Psychological Association(6th ed.)［M］.Washington，DC:Author，2010.

［2］Batterham，A.M.＆ G.Atkinson.How Big does My Sample Need to Be?A Primer on the Murky World of Sample Size Estimation ［J］.Physical Therapy in Sport，2005(6)3:153－163.

［3］Cohen，J.Statistical Power Analysis for the Behavioral Sciences［M］.New York:Academic Press，1969.

［4］Cohen，J.Statistical Power Analysis for the Behavioral Sciences［M］.New York:Academic Press，1977.

［5］Cohen，J.Statistical Power Analysis for the Behavioral Sciences［M］.Hillsdale，NJ:Lawrence Erlbaum Associates，1988.

［6］Ellis，P.D.The Essential Guide to Effect Sizes:Statistical Power，Meta－Analysis，and the Interpretation of Research Results［M］. Cambridge: Cambridge University Press，2010.

［7］Erdfelder，E.，F.Faul＆ A.Buchner.G*POWER:A General Power Analysis Program ［J］.Behavior Research Methods，Instruments，＆Computers，1996，(28)1:1–11.

［8］Faul，F.，E.Erdfelder，A.G.Lang＆ A.Buchner.G*Power 3:A Flexible Statistical Power Analysis Program for the Social，Behavioral，and Biomedical Sciences［J］.Be-havior Research Methods，2007(39)2:175－191.

［9］Hallahan，M.＆ R.Rosenthal.Statistical Power:Concepts，Procedures，and Applications［J］.Behaviour Research and Therapy，1996，(34)5/6:489－499.

［10］Heppner，P.P.，B.E.Wampold＆ D.M.Kivlighan，Jr.Research Design in Counseling(3th ed.)［M］.Belmont，CA:Thomson Brooks/Cole，2008.

［11］Hunter，J.E.＆ F.L.Schmidt.Methods of Meta-Analysis:Correcting Error and Bias in Research Findings(2nd ed.) ［M］. London:Sage Publications Ltd.，2004.

［12］Lan，L.＆ ZW.Lian.Application of Statistical Power A-nalysis–How to Determine the Right Sample Size in Human Health，Comfort and Productivity Research［J］.Building and Environment，2010，(45)5:1202－1213.

［13］ Mayr，S.，E.Erdfelder，A.Buchner ＆ F.Faul.A Short Tutorial of G*Power［J］.Tutorials in Quantitative Methods for Psychology，2007，(3)2:51－59.

［14］Murphy，K.R.＆ B.Myors.Statistical Power Analysis:A Simple and General Model for Traditional and Modern Hypothesis Tests(2nd ed.)［M］.Mahwah，NJ:Lawrence Erlbaum Associates，2004.

［15］Shadish，W.R.，T.D.Cook＆ D.T.Campbell.Experimental and Quasi-Experimental Designs for Generalized Causal Inference［M］.Boston:Houghton Mifflin Company，2002.

［16］鲍贵.多元回归分析中的交互作用问题——以语言阈限假设检验为例［J］.外国语文，2012(4):63－68.