风力发电机微机保护算法研究

刘 军,杨正理

(江苏长天智远交通科技有限公司 三江学院,南京 210012)

0 引言

目前，在对可再生能源的开发中，风力发电是除水能、太阳能外，技术最成熟、最具有大规模开发价值和商业开发条件的发电形式。我国是能源利用大国，但随着化石能源的日趋减少，价格不断上涨和自然环境的恶化，风力发电无疑是一种利好的能源补足形式，因而日益受到我国的重视。

风力发电机组是风力发电系统中的重要组成部分，其造价昂贵、结构复杂。发电机组的正常安全运行，对电力系统的安全、稳定运行起着极为重要的作用。风力发电机组一旦发生故障，对电网的冲击较大；而其损坏也是不可逆的，经济损失巨大。因而当发电机组发生故障时，继电保护装置必须快速将故障切除，才能使损坏降到最少。

现代微机保护装置是基于故障前后的电气量特征构成的，因而实现电气量的准确检测，是微机保护实现对电气元件保护的先决条件。全波傅里叶算法是目前电力系统微机继电保护中被广泛采用的算法。本文通过对风力发电机的微机电流保护所采用的全波傅里叶算法采用MATLAB方法进行辅助设计和分析，验证了该算法在风力发电机微机保护中的实用性。

1 全波傅里叶算法简介

全波傅里叶算法的基本思想来自傅里叶级数，利用正弦、余弦的正交函数性质来提取信号中某一频率分量。如果被采样的模拟信号为一个周期性时间函数时，利用傅里叶级数可将其表示为各次谐波的正弦量和余弦量之和。假设某电流信号，其傅里叶级数可表示为

根据傅里叶级数原理，基波分量的正弦、余弦项的振幅 和 分别为

采用微机计算式（6）的 和 积分值时，通常采用的是有限项求和的方法，即将 用各采样值代入，通过梯形法求和的方法取代积分值。如果对 的基波电流进行采样，每周波采样点为 ，采样周期为 ，考虑基波周期 ， ,则基波分量的正弦、余弦项的振幅 和 计算方法分别为

式中， 为第 次采样值； 和 为 和 时的采样值。

当每周波采样点 ，采样间隔 为 时有

2 全波傅里叶算法的频率响应

对离散计算表达式（7）进行求其 变换，得

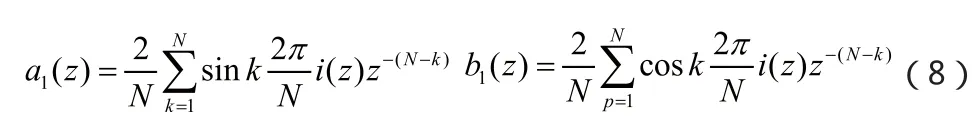
由式（8）可以看出，基波分量的正弦、余弦幅值的求取方法的实质是利用有限长单位冲激响应滤波器滤波器(FIR)进行计算的，而FIR滤波器的单位冲激响应序列为

采用MATLAB分析方法，得到基波分量的正、余弦幅值的频率特性如图1所示。

对基波分量的正、余弦幅值的计算过程是非线性的，因此难以采用图1所示的正弦、余弦幅值的频率特性直接得到傅里叶幅值的频率特性。为了分析全波傅里叶算法的频率特性，设 次谐波分量电流信号

式中， 表示谐波次数， 表示基波频率， 表示 次谐波的初相角。则 次谐波分量的第 个采样点值为

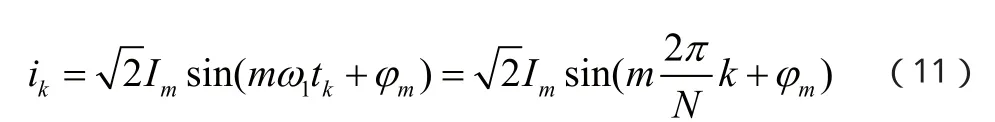
利用全波傅里叶算法求取 次谐波分量的有效值时，定义为相对频率 的幅频特性。

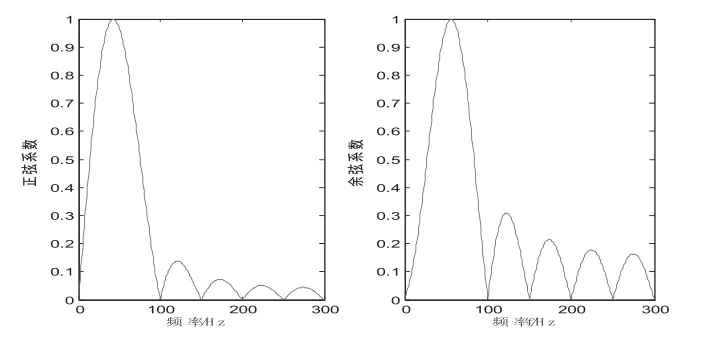
图1 傅里叶正、余弦系数滤波器的频率特性

利用MATLAB分析方法，可以得到在不同初相角情况下全波傅里叶算法的幅频特性如图2所示。由图中可以看出，在不同的初相角下，全波傅里叶算法对于基波、直流分量和各整次谐波分量的频率响应是一样的，但对非整次谐波分量的频率响应却有较大的差别。这一现象说明，全波傅里叶算法只能消除直流分量和整次谐波分量，但不能滤除非整数次谐波分量。在实际应用中，必须注意这一现象，否则得到的结果将不准确，最终会影响到风力发电机的微机保护可靠性。

图2 不同相角情况下全波傅里叶算法的帧频特性

3 结论

从图2中可以看出，采用全波傅里叶算法求取微机继电保护的各电气量参数时，数据窗的长度为一个周波，它用较长的数据窗长度换取了良好的滤波效果和计算的准确性。但应该注意，全波傅里叶算法本身虽然具有完全滤除输入信号中的直流分量和各整次谐波的能力，但在风力发电机出现短路故障时，故障信号中除了整数次谐波外，还具有衰减的直流分量。衰减的直流分量的频谱为连续谱，连续谱与信号中的基频分量会产生频谱混叠现象，从而导致采用全波傅里叶算法求取微机继电保护电气参数时出现误差。因此，在实际运用过程中，应结合相应的滤波器，首先对故障信号进行滤波，再采用全波傅里叶算法，或采用改进的全波傅里叶算法。

[1]于群,曹娜编.MATLAB/Simulink电力系统建模与仿真[M],北京：机械工业出版社,2011(05).

[2]杨正理,黄其新.小波变换在行驶车辆检测器中的应用研究[J],公路交通科技,2013(206)2:104-108

[3]笪丽琴.基于DSP的微机继电保护研究[J].南昌大学硕士论文,2007(12).

[4]何正友,蔡玉梅,王志兵,等.电力暂态信号小波分析的后处理方法研究[J].电网技术,2005(21):46-50.

[5]储呈阳.继电保护技术在电力系统中的应用与前景展望[J].现代企业教育,2012(07).

[6] Mallat S. Hwang W.L. Singularity detection and processing with wavelets[J]. IEEE transactions on information theory,1992(2 Part 2):617-643.

[7]Kaewpijit S, Le Moigne J, El-Ghazawi T, Automatic reduction of hyperspectral imagery using wavelet spectral anlysis[J]. IEEE transactions on Geoscience and Remote Sensing, 2003(4 Part 1):863-871.