等离子热障涂层构件高温热疲劳寿命预测研究

齐红宇，马立强，李少林，杨晓光，王亚梅，魏洪亮

（1北京航空航天大学 能源与动力工程学院，北京100191；2先进航空发动机协同创新中心，北京，100191）

热障涂层防护技术是为满足先进高性能航空发动机发展的需要于20世纪60年代开发出来的一种先进热防护技术[1，2］。热障涂层一方面利用陶瓷材料优越的耐高温、抗腐蚀和低导热等性能，提高热端部件抗高温腐蚀能力；另一方面，可以在保持原有设计的基础之上，减少用作叶片冷却的空气量。因此，从这两个方面来看都提高了整个发动机的推力。热障涂层最初的应用仅仅局限于航空发动机燃烧室的加力筒体和火焰筒等部位，而后随着制备技术的发展，已逐渐应用于导向叶片和转子叶片[3，4］。目前，热障涂层技术已成为研制新一代高推重比发动机的关键技术之一。

热障涂层在制备过程中，涂层内部会形成复杂的界面形貌，高温时粘接层将发生氧化现象，出现热生长层（Thermally Grown Oxide，TGO）[5－8］。这些因素的存在更进一步提高了热障涂层强度与寿命分析的难度，这是一种类似复合材料的非均质、跨尺度及非等向性的力学问题。因此，有必要对这一复杂问题做细致和深入的分析，使热障涂层技术的应用更加趋于成熟与完善。

本工作以某等离子热障涂层的高压涡轮导向叶片为对象，重点开展热障涂层寿命预测技术的研究。由于涡轮导向叶片紧邻燃烧室出口，处于高温、高腐蚀和高速燃气共同作用的工作环境中，保护基体合金的涂层一旦剥落，叶片将因为高温烧蚀而发生失效，所以必须确保热障涂层在工作过程中不出现较大面积的剥落[9，10］。因此，需要准确预测叶片表面涂层在给定工作载荷下的使用寿命，这样不仅可以减小设计风险，而且能够在最大程度上发挥其使用效能，从而达到降低发动机使用和维护成本的目的。

热障涂层寿命预测研究起始于20世纪80年代，最初由美国NASA的Lewis中心建立了一个适用于实验室条件的唯象学模型[11］。进入21世纪后，又出现了以基于材料缺陷尺度[12－14］、损伤力学[6，7］和断裂力学（如预埋主裂纹）[15］等寿命模型。以上寿命预测模型都建立在热障涂层失效和损伤机理的研究之上，而这些研究目前大多只停留在宏观基础之上，如对金属粘接层的氧化现象，只关注了氧化增重和氧化层厚度的增加等宏观量，把这些量引入了寿命预测模型，得到的结果存在一定的误差。所以寻求更准确更适合于工程应用的热障涂层寿命模型对热障涂层体系的进一步发展具有重要意义。

鉴于传统寿命模型对涂层损伤机制描述不足，本工作提出了一种基于Al贫化损伤的热疲劳寿命的预测方法。该预测方法不仅考虑了氧化层厚度的非均匀增长导致的应力重新分布，还考虑了界面形貌影响应力应变分布。同时对粘接层的氧化损伤提出利用粘接层铝浓度作为损伤参量描述氧化损伤，并引入寿命模型。结合圆管构件热疲劳寿命实验数据，获得了寿命预测模型参数，由此建立了带等离子涂层结构的热疲劳寿命预测模型。

1 带TBC构件氧化实验和热疲劳实验研究

1.1 热障涂层氧化实验

选用DZ125合金作为基体材料，线切割成20mm×10mm×2mm的长方体。采用大气等离子喷涂方法制备双层结构的涂层，其中粘接层（Bond Coat，BC）成分为 MCrAlY（Ni－25Cr－5Al－0.5Y），厚度约为150μm；陶瓷层（Top Coat，TC）成分为YSZ（7%Y2O3稳定的ZrO2，质量分数），厚度约为250μm。恒温氧化实验在高温箱式炉中进行。考虑到试样在多次冷却的过程中，涂层的边缘部分可能会发生剥落，因此实验过程中将试样放置在刚玉坩埚内，这样就保证了实验结果的准确性。

1.2 等离子涂层构件热疲劳实验

考虑到带涂层涡轮导向叶片的结构及工作环境特点，实验中采用带涂层薄壁圆管构件来模拟涡轮导向叶片前缘的几何特征。采用高频感应加热的方法对圆管中部进行集中加热，并且在降温过程中采用压缩空气强迫冷却的方式，来达到使试件快速冷却的目的。考虑到加热用感应线圈的直径以及有效加热范围，等离子涂层圆管构件内径设计为11mm，外径为15mm，长度为85mm，如图1所示。圆管基体材料为定向结晶高温合金DZ125。热障涂层中粘接层、陶瓷层的成分和厚度均与1.1节相同。

图1 等离子涂层圆管结构示意图Fig.1 Schematic drawing of the plasma sprayed coatings tube structure

选取1050℃作为带热障涂层圆管热疲劳实验的最高温度，实验最低温度设定为100℃。采用三角形和梯形循环谱作为实验载荷条件。只考虑热疲劳损伤时采用三角波，其中加热段时间设定为120s，冷却段时间设定为300s。考虑热疲劳损伤和氧化损伤的耦合效应时，采用梯形波，其中加热段时间和冷却段时间与三角形循环载荷谱相同，高温保持时间设定为670s。考虑到热障涂层内部氧化层厚度不同对于涂层热疲劳寿命的影响，实验中对部分构件分别进行了50，100，200h的高温（1050℃）预氧化处理。带热障涂层圆管热疲劳寿命实验结果如表1所示。

表1 带涂层圆管热疲劳寿命实验结果Table 1 Thermal fatigue test result of tube coated with TBC

2 热疲劳寿命预测模型的建立

2.1 粘接层Al贫化模型的建立

图2为涂层在等温氧化不同阶段的扫描电镜图片，沉积态的粘接层包含内部条形的氧化物，如图2（a），此氧化物在喷涂期间形成[16－18］；经过180h等温氧化后，观察到两个氧化铝的贫化区，一个靠近基体，另一个靠近TGO层，如图2（b）所示；在1050℃氧化300h后，条形的氧化铝严重消耗，在粘接层中观察到不连续的点状结构，见图2（c）。

图2 涂层在1050℃氧化不同阶段的扫描电镜图（a）沉积态；（b）氧化180h；（c）氧化300h；（1）TC／BC界面；（2）BC／Sub界面Fig.2 SEM images of cross－sections revealing the bond coat before and after isothermal oxidation at 1050℃（a）as－deposited；（b）after 180h；（c）after 300h；（1）TC／BC interface；（2）BC／Sub interface

通过对高温氧化实验结果的观察和分析，定性地得到了粘接层中的Al分别向粘接层表面和基体扩散的特征，为了进一步定量描述粘接层中Al浓度的变化，本工作将根据扩散的菲克定律[19，20］，结合实验数据建立粘接层Al贫化的数学模型。

假定Al元素经高温氧化后在粘接层和基体中某位置平均含量均匀一致。根据扩散的菲克第二定律式（1），对于热障涂层／粘接层界面（TBC－BC）和粘接层／基体界面（BC－Sub）给出不同的初始条件，得到扩散方程的解，可以评估Al元素在高温氧化过程中的扩散规律。

根据扩散的菲克第二定律式

对于热障涂层／粘接层界面和粘接层／基体界面给出不同的初始条件，得到扩散方程的解，可以评估Al元素在高温氧化过程中的扩散规律。

模拟TBC－BC界面时，初始条件为：

CBC为未氧化时粘接层中Al浓度，hBC为氧化t小时后粘接层厚度，hTGO为t时刻TGO层厚度，x为Al元素扩散的距离。

根据方程（1）和方程（2）的可以得到：

对于粘接层和基体边界，初始条件为：

CSub为t＝0时基体中Al元素浓度。方程（1）的解为：

根据扩散的叠加原理，将式（3）与式（5）相加，得到的粘接层Al贫化的数学模型：

在1050℃氧化后，粘接层和基体中模拟的平均Al浓度分布见图3，由式（6）绘制曲线得到。图3表明在氧化过程中，粘接层中Al元素浓度的变化，即随着氧化的进行，Al向粘接层两边扩散，粘接层中Al浓度逐渐减少。图3中模拟的平均Al浓度分布与前面所观察到的两个富铝相的贫化相对应。电子探针测得的垂直氧化层／粘接层界面方向平均Al浓度值为图3中的点，可以看出实验结果与模拟结果相符合。通过建立描述粘接层中Al扩散行为的数学模型，将粘接层Al浓度作为表征氧化损伤的控制参量引入寿命预测模型，为下一步建立更为准确的寿命模型值奠定了基础。

图3 高温氧化后粘接层和基体中模拟的平均Al浓度分布及部分测量与模拟浓度分布对比Fig.3 Comparison of the measured and modeled Al distribution

把Al浓度作为控制参量引入寿命模型，还有一个需要考虑的是选取合适位置的浓度值。本工作取在粘接层厚度方向上对Al浓度变化曲线积分值，则可得到粘接层中铝浓度随时间的变化规律c（t）（简记为c），如图4所示。

图4 涂层中粘接层中Al浓度随着氧化时间的变化Fig.4 Al content of internal oxide in the bond coat as function as oxidation time

2.2 等离子涂层热疲劳寿命预测模型的建立

根据传统的Manson－Coffin理论，确定热障涂层循环寿命预测的基础模型的基本表达式为：

其中，Nf为循环次数；Δε为危险部位的工作应变范围；Δεf为静载荷作用下失效时，涂层危险点的应变范围（循环寿命Nf＝1）；b为经验指数，通过疲劳实验确定。

由于热障涂层失效是粘接层氧化及热不匹配综合作用的结果，上述热障涂层循环寿命预测的基础模型仅仅反映出热不匹配的影响，未考虑高温氧化损伤的作用。本工作引入粘接层中Al浓度作为耦合氧化损伤的控制参量，提出一种新的寿命预测模型。

定义损伤变量D氧化＝1－c／c0，其中，c为氧化一定时间后粘接层中的Al浓度；c0为初始无氧化时粘接层中的Al浓度，当c＝c0时，此时只有机械应变对疲劳寿命造成影响，与式（6）相同；当c＝0时，表明氧化已经对热障涂层结构造成完全破坏；当c介于0和c0之间时，氧化和机械应变共同对涂层的寿命造成损伤。由于氧化的存在使热障涂层寿命降低，引入粘接层中铝浓度c作为控制参量，得到热障涂层热疲劳寿命预测模型：

其中，a为模型参数，需要通过实验数据获得。该修正模型适用工况为恒幅循环载荷，对于随机载荷条件下的寿命预测可以引入累积损伤的概念。根据Miner线性累积损伤模型，假设在某种载荷作用下循环一次造成的损伤为Dm＝1／Nm，则随机载荷工况下的损伤总计为：

其中，Dm为第m 种循环载荷对圆管的损伤，Nm代表第m种循环载荷工况下的循环寿命，nm为该工况下的循环次数，k为不同循环的总数。上式可以表示为：

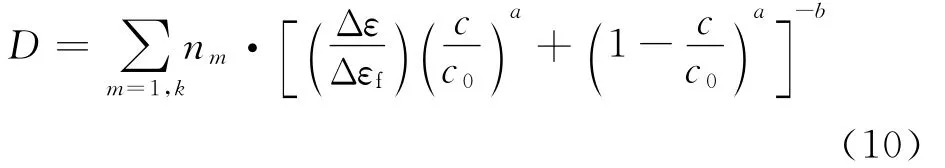
当累积损伤系数D≥1时，涂层失效。

3 等离子涂层圆管热疲劳分寿命预测

3.1 等离子圆管有限元计算

热障涂层由于陶瓷层与粘接层之间界面粗糙，在其周围很容易产生应力集中，正常情况下涂层失效部位应该在陶瓷层内并位于粘接层／陶瓷层界面附近，而且在整个循环周期里此处会出现非弹性变形对圆管进行有限元分析，主要目的是通过计算分析，确定危险点位置，并选取合适的应力或应变范围分量来作为衡量结构体系寿命的控制参量，对其进行寿命预测研究。

寿命公式中的Δε对于涂层来说表示为在一个完整的循环周期中，危险点处的非弹性应变范围，这个控制参量可以通过有限元计算得到。本工作根据对陶瓷层内界面附近应力场的计算结果，在对其进行寿命建模时，采用陶瓷层界面附近危险点的应变范围作为控制参量。

建立带等离子热障涂层的圆管有限元模型（如图1所示），进行高温热循环载荷作用下的应力应变计算。热障涂层系统中陶瓷层厚0.25mm，粘接层厚0.125mm。根据扫描电镜图片图3，考虑界面粗糙度及热生长氧化层TGO厚度的影响，选用正弦曲线模拟涂层界面形状，波长25.725μm，幅值7.94238μm。分别建立 TGO厚度为0，2，4，6，8μm和10μm六种情况下的4结点二维轴对称有限元模型，如图5所示。

危险点处的径向应变范围、剪切应变范围和轴向应变范围随氧化层厚度的变化曲线如图6所示，当氧化层厚度为零时，危险点处的剪切应变范围较大；随着氧化层厚度的增加，剪切应变范围经历了先减小后增大的过程，而轴向应变范围的变化趋势则刚好相反。可见，氧化层厚度的不同将极大影响陶瓷层界面附近的应力状态。

3.2 等离子涂层圆管热疲劳寿命预测分析

图5 圆管有限元模型示意图Fig.5 Axisymmetric FE model of the plasma sprayed coatings tube structure

图6 陶瓷层内部危险点处应变范围随着TGO厚度变化曲线Fig.6 Strain range with TGO thickness at critical point

在获得带热障涂层圆管热疲劳寿命实验结果后，分别采用轴向应变范围Δεa，径向应变范围Δεr，轴向和剪切等效应变范围以及径向和剪切等效应变范围进行参数的拟合计算。由已经得到的陶瓷层内应变范围和粘接层Al浓度，结合1～6号试样的实验结果，对修正的寿命预测模型中的参数a，b和Δεf0进行非线性拟合，结果见表2。

表2 热障涂层圆管热疲劳寿命预测模型参数Table 2 Thermal fatigue life prediction model parameters of the plasma sprayed coatings tube structure

1～6号试样的寿命的拟合值和实验值如图7所示，可以看出所有寿命值均处于±1.5倍分散带之内，这说明所建立的寿命预测模型是适用的。

图7 等离子涂层圆管寿命实验值与拟合值Fig.7 Thermal fatigue test and prediction data of parameters of the plasma sprayed coatings tube structure

4 结论

（1）根据菲克第二定律建立粘接层Al贫化的数学模型，模拟高温下粘接层中Al向粘接层表面和基体扩散的行为。

（2）把粘接层Al浓度作为耦合氧化损伤的控制参量引入已有的寿命预测模型，建立基于微观特征的可以体现氧化损伤与热疲劳损伤耦合效应的等离子热障涂层寿命预测模型，并根据热疲劳实验结果，使用线性回归的方法拟合寿命模型中的相关参数，涂层热疲劳寿命的拟合值处于±1.5倍分散带之内。

[1]MILLER R A.Current status of thermal barrier coatings－an overview[J］.Surface and Coatings Technology，1987，30（1）：1－11.

[2]韩萌，黄继华，陈树海.热障涂层应力与失效机理若干关键问题的研究进展与评述[J］.航空材料学报，2013，33（5）：83－98.HAN M，HUANG J H，CHEN S H.Research progress and review on key problems of stress and failure mechanism of thermal barrier coating[J］.Journal of Aeronautical Materials，2013，33（5）：83－98.

[3]SHEFFLER K D，GUPTA D K.Current status and future trends in turbine application of thermal barrier coatings[J］.Journal of Engineering for Gas Turbines and Power，1988，110（4）：605－609.

[4]钟锦岩，牟仁德，何英，等.NiCoCrAlYHf涂层与一种Ni基单晶高温合金循环氧化行为研究[J］.材料工程，2013，（8）：28－35.ZHONG J Y，MU R D，HE Y，etal.Thermal cyclic oxidation behavior between NiCoCrAlYHf bond coat and a kind of Ni－based single crystal superalloy[J］.Journal of Materials Engineering，2013，（8）：28－35.

[5]SCHLICHTING K W，PADTURE N P，JORDAN E H，etal.Failure modes in plasma－sprayed thermal barrier coatings[J］.Materials Science and Engineering：A，2003，342（1）：120－130.

[6]BUSSO E P，LIN J，SAKURAI S，etal.A mechanistic study of oxidation－induced degradation in a plasma－sprayed thermal barrier coating system Part I：model formulation[J］.Acta Materialia，2001，49（9）：1515－1528.

[7]BUSSO E P，LIN J，SAKURAI S，etal.A mechanistic study of oxidation－induced degradation in a plasma－sprayed thermal barrier coating system Part II：life prediction model[J］.Acta Materialia，2001，49（9）：1529－1536.

[8]CHEN W R，WU X，DUDZINSKI D.Influence of thermal cycle frequency on the TGO growth and cracking behaviors of an APSTBC[J］.Journal of Thermal Spray Technology，2012，21（6）：1294－1299.

[9]KERREBROCK J L.Aircraft Engines and Gas Turbines[M］.Cambridge，MA：MIT Press，1992.

[10]HE M Y，MUMM D R，EVANS A G.Criteria for the delamination of thermal barrier coatings：with application to thermal gradients[J］.Surface and Coatings Technology，2004，185（2）：184－193.

[11]DEMASI J T，SHEFFLER K D，ORITIZ M.Thermal Barrier Coating Life Prediction Model Development[R］.NASA－CR－182230，1989.

[12]EVANS A G，MUMM D R，HUTCHINSON J W，etal.Mechanisms controlling the durability of thermal barrier coatings[J］.Progress in Materials Science，2001，46（5）：505－553.

[13]EVANS A G，HE M Y，HUTCHINSON J W.Mechanics－based scaling laws for the durability of thermal barrier coatings[J］.Progress in Materials Science，2001，46（3）：249－271.

[14]HE M Y，EVANS A G，HUTCHINSON J W.The ratcheting of compressed thermally grown thin films on ductile substrates[J］.Acta Materialia，2000，48（10）：2593－2601.

[15]QIAN G.Fracture Analysis and Microstructural Modeling of Thermal Spray Coatings[D］.New York：School of Mechanical Engineering，State University of New York，USA，1999.

[16]BRODIN H，ESKNER M.The influence of oxidation on mechanical and fracture behaviour of an air plasma－sprayed NiCo－CrAlY bondcoat[J］.Surface and Coatings Technology，2004，187（1）：113－121.

[17]CHEN W R，WU X，MARPLE B R，etal.Oxidation and crack nucleation／growth in an air－plasma－sprayed thermal barrier coating with NiCrAlY bond coat[J］.Surface and Coatings Technology，2005，197（1）：109－115.

[18]EVANS H E，TAYLOR M P.Diffusion cells and chemical failure of MCrAlY bond coats in thermal－barrier coating systems[J］.Oxidation of Metals，2001，55（1－2）：17－34.

[19]王亚梅.热障涂层破坏机理及寿命分析方法的研究[D］.北京：北京航空航天大学，2009.

[20]CHE C，WU G Q，QI H Y，etal.Depletion model of aluminum in bond coat for plasma－sprayed thermal barrier coatings [J］.Advanced Materials Research，2009，75：31－35.