结合属性重要度和灰色关联度的数据补齐方法

王方心，潘 巍，吴立锋，金声震，李晓娟

（1.首都师范大学 信息工程学院，北京100048；2.首都师范大学 高可靠嵌入式系统技术北京市工程研究中心，北京100048；3.首都师范大学 电子系统可靠性技术北京市重点实验室，北京100048）

0 引 言

在模式识别中，人们通过对各种形式的数据进行处理和分析，进而对事物和现象进行描述、辨认、分类和解释。上述过程主要是通过对数据的聚类和分类来实现的。传统的识别方法 （如基于决策树模型的ID3算法、基于统计模型的贝叶斯分类方法和基于神经网络的数据分类方法等等）对属性完备的数据的处理和分类已经取得了令人满意的效果，应用也比较广泛。

然而，在实际获取信息的过程中，由于种种原因，所得到的数据往往是不完备的［1］，这主要是由以下几个方面造成的：①有些信息暂时无法获取；②有些信息可能是因为输入时认为不重要、忘记填写或对数据的理解错误而遗漏；③由于数据采集设备的故障、存储介质的故障、传输媒体的故障、一些人为因素等原因丢失；④有些对象的某个或某些属性是不可用的；⑤有些信息是被认为不重要的；⑥获取某些信息的代价过大；⑦系统实时性要求较高，即要求得到这些信息前迅速做出判断或决策。由于现今比较常用的识别方法大多针对完备数据，当存在数据缺失，尤其是关键属性的数据缺失时，经常会给数据分析造成干扰，如①数据处理效率的下降；②分析和处理数据时复杂性的增加；③不完备数据和完备数据间的偏差，而这些干扰会给后续的决策以及响应造成诸多不便。

目前，已经有一些方法来解决属性值缺失时的数据处理与分类问题，它们主要基于以下3个思路：①直接将具有缺失数据的样本删除［2］，这种方法主要应用于数据缺失量较少而且删除的样本数据对最终结果的分析不会造成重大影响的情况。当缺失数据较多时，这类方法往往会丢失大量有用信息［3］；②使用能够处理缺失数据的识别方法，但这类方法一般计算复杂度较高，应用场合也比较有限；③当具有缺失数据的样本较多但每个样本缺失的数据相对较少时，通过研究数据属性之间的分布状况，可首先对缺失的数据进行补齐，然后再利用已有的对完备数据进行处理的方法进行识别。用这类方法补齐的数据能够较好地保留数据的原有信息，是解决数据缺失问题的一种比较好的途径。

根据数据样本的分布状况进行数据补齐的主要思路是在完备数据子表中找出不完备样本的完备近邻，并利用这些完备近邻的相应属性值对不完备样本的缺失数据进行补齐，如KNN等方法。在距离测度上，通常可以使用欧氏距离、马氏距离和灰色关联度等。此外，大量的研究表明，属性的重要程度对于数据的处理也起着非常重要的作用。例如，采用属性重要度加权的欧氏距离来计算样本之间的距离能够提高聚类的正确率［4］。

综上，本文结合属性重要度和灰色关联度，提出了一种新的数据补齐方法。首先，按照属性重要度确定各个属性的补齐顺序；其次，对于当前要补齐的缺失样本，将所有完备样本分别与其进行两两比较，并选择灰色关联度最大的完备样本对样本进行补齐。实验结果表明，即使在很高的数据缺失比率下，本文方法仍能很好地进行补齐，并能取得较高的识别率，是一种理想的数据补齐方法。

1 常用的数据补齐方法

数据补齐方法主要通过研究数据表中每个属性下各个值之间 （纵向）或每条样本之间的 （横向）关系得到数据分布的规律和模型，进而对缺失属性进行合理的推断和补齐。这些方法包括：均值法：该方法用完备数据集中需被补齐属性的平均值来进行补齐，使用起来比较方便、计算量较小，在属性值分布较为集中时能够取得比较好的效果；概率法：该方法通过统计每个属性中各个值的出现频率，从中找出出现频率最大的值进行缺失数据的补齐，使用起来也较为简便；回归预测法［5，6］：该方法通过分析每条样本中各个属性之间的关系，建立各个属性之间的关系模型，进而对缺失数据进行回归预测和补齐；多重插补的方法［7］：该方法估计出待插补的值，然后再加上不同的噪声，形成多组可选插补值，最后根据某种选择依据，选取最合适的插补值；Hot Deck和Cold Deck补齐方法：该方法在完备数据中寻找与缺失数据在某种距离上最为接近的一个或多条样本，利用这些样本的属性值对缺失数据进行补齐，使得结果更加合理和准确。Hot Deck利用缺失数据的样本所在的数据集的完备数据进行补齐，Cold Deck则利用另一张同类的数据表对缺失数据进行补齐。事实上，距离尺度的选择以及如何利用距离最近的属性值进行补齐都是影响最终效果的重要因素，目前常用的距离尺度包括欧氏距离、马氏距离、隶属度函数和灰色关联度等。文献 ［8］中提出一种利用基于灰色关联度的KNN的数据补齐算法，但由于KNN算法本身的缺陷［9］使得该方法在使用上有所限制。文献 ［10］提出一种利用灰色关联度进行重复补齐的方法，首先用平均值法进行补齐，再计算不完备数据与完备数据的灰色关联度，并选择近邻数据进行二次补齐，并由此进行多次补齐直至与前一次补齐的数据值偏差达到收敛；这样的收敛条件一是会影响补齐算法的速度，不适合在实时性要求较高的场合中使用，二是不当的收敛条件会使得补齐过程陷入局部的死循环，给数据补齐造成困难。

2 基于属性重要度和灰色关联度的数据补齐方法

本文提出了属性重要度和灰色关联度相结合的数据补齐方法。首先，计算每个属性的重要度，并以此确定数据补齐时的先后顺序；其次，针对当前要补齐的样本，利用灰色关联度，在完备数据集中找出与其关联度最大的完备数据，对当前样本的缺失数据进行补齐。

2.1 属性重要度

多数情况下，人们假设数据集的属性是完全随机缺失（MCAR）的，并且完备数据与不完备数据的分布特性是相同的。因此，为了使得数据更加便于识别，所使用的距离衡量尺度应该能够反映原有数据的分布特点。同样，数据的补齐过程也应该能够体现这些特点。在一张数据表中，每个条件属性都会影响决策属性，各个条件属性值的共同影响使得数据在多维空间上呈现出特定的空间关系，而这种关系会最终影响识别的结果。与此同时，每个条件属性对决策属性的影响又是不同的，在由与决策属性关联度较高的条件属性组成的空间中，不同类别的数据能够较为清晰地被分辨出来，而在由与决策属性关联度较低的条件属性组成的空间中，不同类别的数据分布较为混乱 （如图1所示）。因此，属性的重要度可以作为一个能够体现原始数据分布特点的参数。

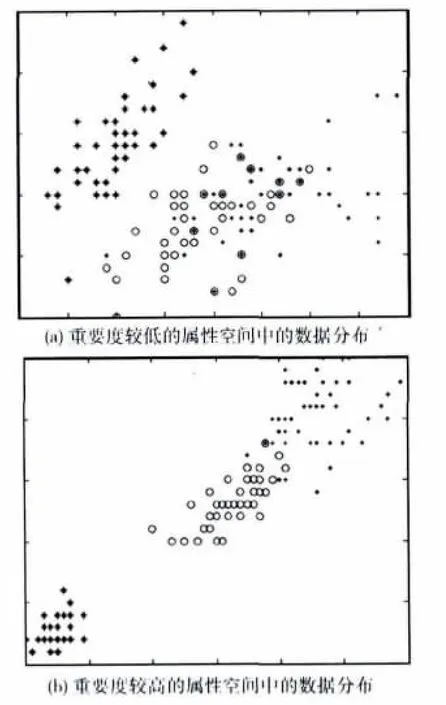
图1 不同属性空间中数据的分布情况

2.1.1 基于属性依赖度的属性重要度［11］

利用属性删除前后的属性集的依赖度之差来计算属性重要度

式中：card（）——集合的势，γ——属性依赖度，R——所有条件属性集合，条件属性C∈R，为X的下近似集，sig（C）为属性C的相对依赖度。这种计算属性重要度方法表征了该属性对于整个论域的分类能力的贡献大小。

2.1.2 基于互信息熵的属性重要度计算方法［12］

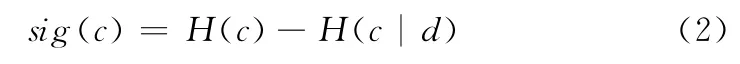
式中：H （·）——该属性的熵，c——条件属性，d——决策属性。这种方法利用条件属性与决策属性之间互信息的大小来衡量属性的重要程度，用信息论的观点对条件属性的性质进行分析。

2.1.3 本文的属性重要度定义

本文中，属性重要度的计算方法如下，假设数据表中样本的任意一个条件属性为C，决策属性为Di（i＝1，2，…，m，表示有m个决策类），则条件属性C的属性重要度为

式中：Maxi、Mini——属性C在Di类上的最大值和最小值，di——在 ［Mini，Maxi］上与 ［Mink，Maxk］（k≠i）的非交叉区域。

如图2所示，假设数据表中共有3个决策类 （Y1，Y2和Y3），图中的横线表示条件属性a的属性值的取值范围。

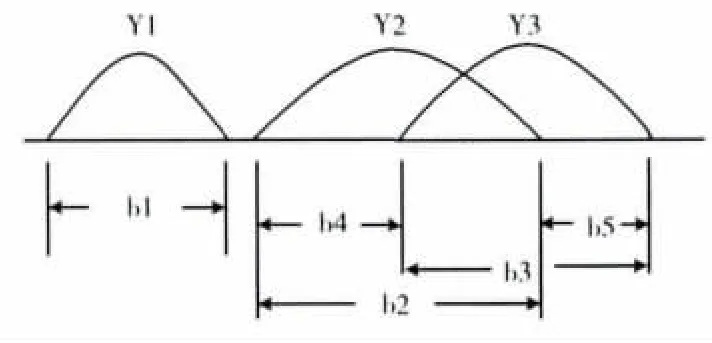
图2 属性重要度的确定

可以发现，在决策类Y1中，属性a的取值范围与其它类别并无交叉部分，所以如果某个样本的属性a的值在此范围内，就可以直接将该样本划归为Y1类。此时，属性a对Y1类的重要度为1。同时，Y2，Y3中，属性a的取值范围有交叉现象，当某个样本的属性a的值出现在交叉区域，就无法直接根据属性a判断该样本的类别，但当某个样本的属性a的值在b4段或b5段时，仍能仅根据属性a判断其类别。因此，属性a对某一决策类的重要度为非交叉区域占属性a的总体取值范围的比重大小。如对于Y2来说，属性a的重要度为b4／b2。同样，属性a对全体决策类的重要度为在其对于各个决策类的重要度之和，即b1＋b4／b2＋b5／b3。本文算法中，将据此确定属性重要度，从而确定补齐过程中各个属性的补齐顺序。

相较于传统的属性重要度的定义方法，本文方法更加客观也更加直观，能够清晰地描述各个条件属性对不同决策类别的分类能力：例如，在图2中，属性值在b1范围内的样本一定属于Y1类，利用该属性就能够直接判别样本是否属于Y1类。同理，由于Y2和Y3有交集，因此对于交集范围内的样本，无法仅根据属性a明确地确定归属。综上，这种属性重要度的定义方法能够清楚地刻画某一属性对整个样本分类的重要程度。

2.2 灰色关联度

样本之间的对比往往不是很精确的，做不到非白即黑，此时需要有指标进行衡量。灰色关联度是衡量两个样本相似程度的一种度量方法，它将数据看作是一个灰关联因子集，其中有参考序列和比较序列，每个参考序列与所有比较序列构成灰色子空间，各个灰色子空间构成灰色空间。灰色关联度使用整体比较，是有参考系的、有测度的比较［13］。

若

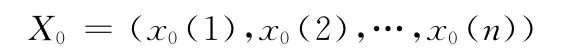
为参考序列

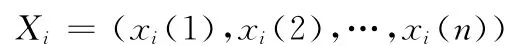
为比较序列。

且定义X0（k）与Xi（k）的关联系数为

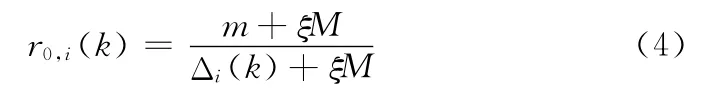
则X0与Xi的灰色关联度为

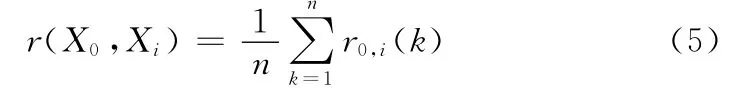
这种关联度的定义方式体现了序列之间对应点的平均相似程度，从这个角度能够较好地体现两个序列的相似性和关联程度。

2.3 数据补齐步骤

为了充分利用不完备数据中的信息，本文会将每一个补齐后的样本加入到原有的完备数据集中，将其用于下一个缺失样本的补齐。在这种情况下，补齐样本的加入顺序对最终的数据识别会产生一些影响。因此，本文首先从最初的完备数据子表中计算每个条件属性的重要度，优先补齐重要度高的属性。这种处理方式一方面可以减少整个数据表在补齐过程中的不确定性，另一方面会为后续缺失样本的补齐提供尽可能多的确定信息。

假设数据表T含有n个条件属性和1个决策属性 （假设共有k个决策类），并且表中有m个样本，每个样本的类标签d为已知。算法具体步骤如下：

（1）将数据表T拆分为完备数据表Tc和不完备数据表Tq。

（2）利用式 （3）计算Tc中的每个条件属性的属性重要度Sig（Ci）（i＝1，2，…，n），并根据Sig（Ci）的大小将Tq中的数据进行重新排序，将缺失重要属性的数据排在前列，优先进行数据补齐，排序后的新表为Tx。例如：若完备表中有4个属性，它们的属性重要度顺序为 ［2，1，3，4］，则在不完备数据表中依次存放缺失第2、1、3、4条属性值的样本数据。当样本同时缺失多个属性时，则按照缺失属性的重要度之和来进行数据补齐，例如，当存在同时缺失2、1属性和缺失2、3属性的样本时，则优先对前者进行数据补齐。

（3）依次取出Tx中的样本t（c1，c2，…，cn，d），根据d的值，找出Tc中决策属性为d的子样本集Tcs，然后分别将t和Tcs中缺失属性所在的列删除。例如：若不完备样本t缺失第二个属性，且t的决策属性为1，则在完备数据表中找出所有决策属性为1的子样本数据集，并删除t和该子样本数据集中所有样本的第二个属性。

（4）根据式 （4）、式 （5）分别计算t和子样本数据集Tcs中每个样本的灰色关联度。

（5）选择Tcs中与t关联度最大的样本，用其对应属性上的值对t中的缺失数据进行补齐。

（6）将补齐后的数据t添加到Tc中，并将其从Tx中删除，重复 （3）、（4）、（5）、（6）直至全部缺失数据补齐完毕，即Tx为空。

3 不完备数据补齐算法的评价方法

在评价数据补齐算法性能的时候，通常采用在原有完备表的基础上，人为地使之缺失某些值，然后利用该算法进行补齐后，比较补齐后的值与原有值的平均误差，以其作为评价补齐算法性能的指标。虽然该评价方法在某种意义上来说是较为有效的，但在某些领域中 （如分类识别），这样的评价方法并不能够有效评估补齐的数据对分类识别性能的影响。另外，通常在实际应用中，原值往往是不存在的，所以该评价方法并不实用。

此外，现实生活中大多数的数据缺失的模式都属于MCAR，而且通常认为具有缺失数据的样本与具有完备数据的样本具有相同的分布特性［5］。因此，一方面，补齐后数据表中的样本数据应该尽可能地被识别，另一方面，数据表中的原有完备数据部分的识别率应当优于补齐前的识别率，即补齐后的数据不能造成原有完备数据识别率的下降。

由此，本文提出了不完备数据补齐算法的评价标准：

（1）比较补齐前后整个数据的识别情况。在数据补齐前，若在完备数据表Tc中能够正确识别的样本个数为g，Tc的样本总数为f，Tq的样本总数为h，则补齐前Tc识别率I1＝g／f；补齐后，Tc的样本总数为m（m＝f＋h），补齐后能够被识别的样本个数为s，则补齐后的识别率I2＝s／m；最后比较I1和I2的值，I2—I1越大则算法越有效。

（2）比较原有完备数据在补齐前与补齐后的识别率变化情况，观察补齐前后属性分布的变化。在进行补齐前，对于Tc，完备数据的识别率为I1；补齐后，再对整个数据表进行识别，其中原有完备数据Tc能够被正确识别的样本数为y，则完备数据的识别率I3＝y／f，则I3—I1越大算法越有效。

4 实验与分析

本实验选用UCI数据库中的Tae（teaching assistance value）（属性值也有离散型也有连续型），Hayes－Roth（属性值均为离散型）和Iris（属性值均为连续型）数据集，分别在属性缺失比例为5%、10%、15%、20%的情况下，每个缺失比例下进行10次实验，分别采用直接将缺失属性数据删除、最大概率法 （如果是离散数据直接用出现频率最高的值进行补齐，如果是连续数据则出现频率最高的邻域的中心值进行补齐；邻域取该属性值的最小间隔）、基于欧式距离的K（k＝6）邻域补齐方法、基于灰色关联度的重复补齐方法［13］和基于属性重要度和灰色关联度的补齐方法对这些缺失属性的数据表进行补齐，最后用留一法对补齐的数据进行识别并计算识别率。结果见表1。

表1 在缺失属性的不同数据集上使用不同方法进行数据补齐后识别的正确识别率

当不使用任何数据补齐方法时，即直接删除含有缺失数据的样本时，3个表的样本识别率随着样本数据缺失比例的增加迅速下降。这样的结果对后

续的识别和分析是不利的，因此对不完备数据进行补齐是十分有必要的。

从表1可以发现，本文方法在对3个具有不同特性的数据集进行补齐后，都能达到最高的分类性能。即使数据集的缺失比率很高时，也能很好地保持系统的分类性能以及识别率。

下面将对上述各个数据表的条件属性分布特点进行分析，以此证明本文所定义的属性重要度能很好地描述各个属性对于分类的重要性。

Tae表共有151个样本，每个样本均有5个属性，共有3个决策类。如表2所示，在原完备数据表中第1个和第4个属性的重要度为0，因为它们的取值仅有1和2，而且在每一个决策类中都存在这两个值，仅依据这两个属性根本不能够确定任何样本的类别。因此，对于仅缺失这两个属性的样本，将其放在最后进行补齐。

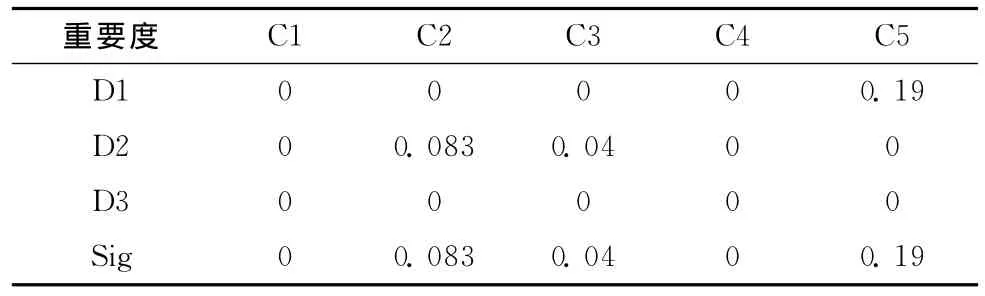
表2 Tae数据表各属性相对各决策属性的重要度和属性重要度

同理，各个条件属性在不同缺失比例下的属性重要度如表3所示，本文据此对具有缺失数据的样本进行排序。

表3 Tae数据表各属性在不同数据缺失比例下的属性重要度 （Sig）

在不同的数据缺失比例下，应用本文方法对Tae数据表进行补齐。在补齐前后，原有完备样本的识别率如图3所示。可以发现，当缺失数据的比例增加后，本方法显示出了鲁棒的性能优势，数据补齐后，原有完备样本的识别率得到了提高。

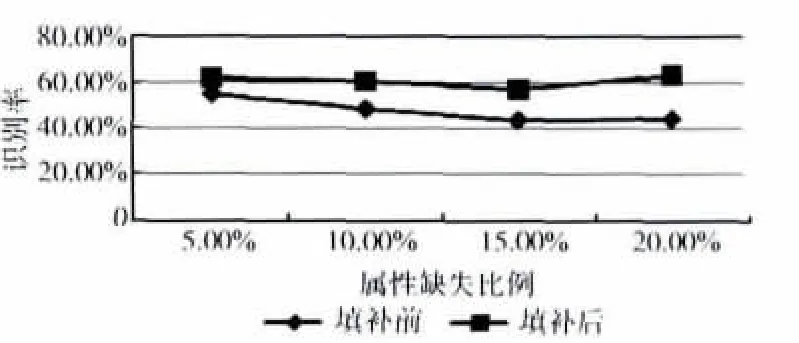
图3 Tae数据表填补前后完备数据识别率比较

Iris表共有150个样本，每个样本均有4个连续属性值，共3类。各属性在数据完备和缺失不同比例数据时的重要度见表4和表5。通过分析可以发现，Iris数据表的第3和第4个属性对于数据分类有着关键作用，特别在类别1中，根据它们即可以直接确定样本的归类，在其它类别中，它们在类与类之间的交叉部分也较小，加之该数据表本身的识别率较高，所以利用各种方法进行补齐之后的识别率相距并不太大。

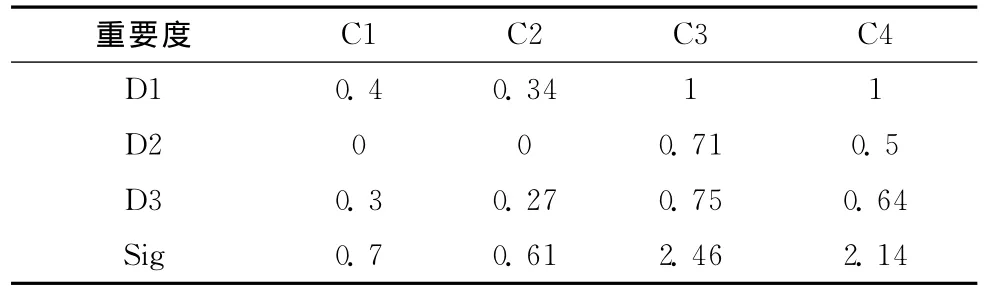
表4 Iris数据表各属性相对各决策属性的重要度和属性重要度

表5 Iris数据表各属性的属性重要度 （Sig）

在不同的数据缺失比例下，应用本文方法对Iris数据表进行补齐。在补齐前后，原有完备样本识别率如图4所示。

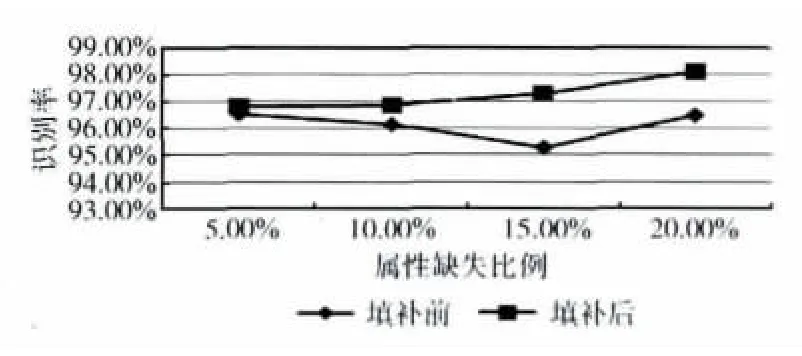
图4 Iris数据表填补前后完备数据识别率比较

实验表明：即使缺失比例不断增加，本文方法仍能显示出良好的性能。对于Iris表而言，虽然在属性缺失比例为5%时，本文方法补齐后的识别率 （95.53%）并不是最高，但依然接近最高识别率 （96%）。

此外，当缺失比例增高时，出现了识别率提升的情况。本文认为，Iris表本身的数据分布已较为清晰，识别率很高，只有少部分数据存在交叉分布的情况。因此，当缺失比例增加时，那些处于交叉区域的样本产生缺失数据的概率也随之增大。此外，本文采用与含有缺失数据样本具有最大关联度的完备样本的相应数据进行补齐，因此这些样本在补齐后会更接近完备样本，其不确定性进一步降低，因此最后的识别率也就会有所升高。

Hayes－Roth表共有160条样本，每个样本均有4个离散属性，共3类。各属性在数据完备和缺失不同比例数据时的重要度见表6和表7。由于此表为离散数据表，且存在大量重复离散值，个别属性值的缺失对属性重要度的影响几乎为0，因此即使在属性缺失比例明显不同的情况下，属性重要度仍基本相同。其中第2个、第3个和第4个属性对决策属性的影响程度相近，而第1个属性对于决策属性的影响几乎为0。

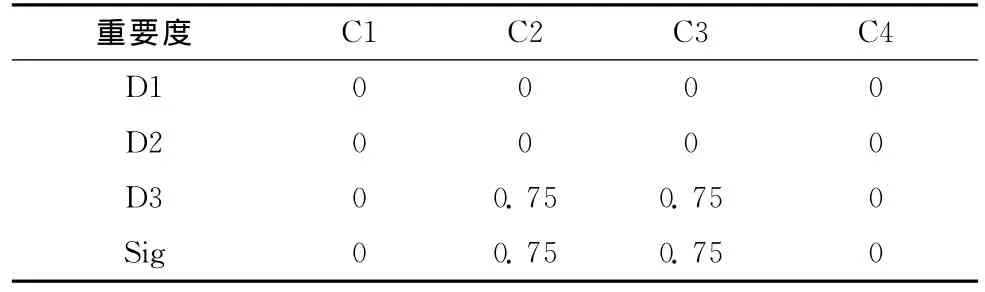
表6 Hayes－Roth数据表各属性相对各决策属性的重要度和属性重要度

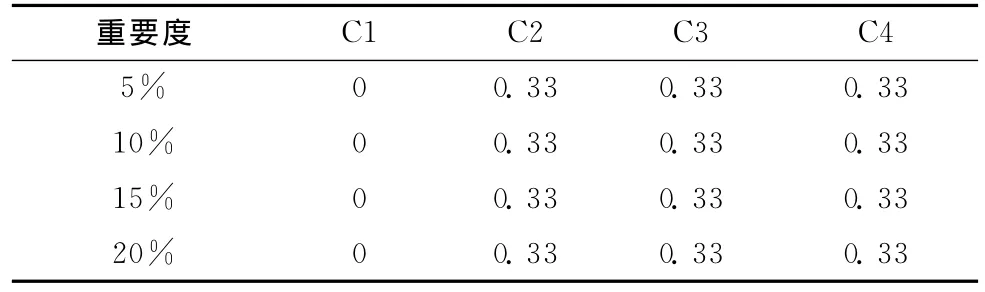
表7 Hayes－Roth数据表各属性的属性重要 （Sig）

在不同的数据缺失比例下，应用本文方法对Hayes－Roth数据表进行补齐。在补齐前后，原有完备样本识别率如图5所示。

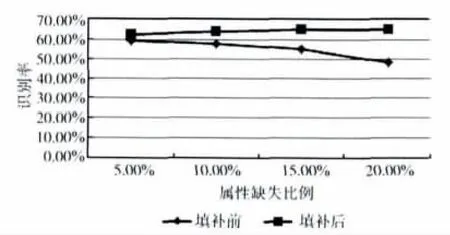
图5 Hayes－Roth数据表填补前后完备数据识别率比较

5 结束语

对缺失数据的数据表进行补齐会引入新的不确定性，它会影响后续的识别和分类效果。本文结合属性重要度和灰色关联度，提出了一种新的数据补齐方法，能使补齐后的数据具有高识别率。同时，本文还提出了判断数据补齐性能的评价标准，即补齐后的数据不能影响原有数据的识别率，它能对数据补齐方法做出客观的评价。实验结果表明，本文方法即使在很高的数据缺失比率下仍能很好地对数据进行补齐，并能取得较高的识别率，是一种理想的数据补齐方法。

［1］Matthias Templ Alexander Kowarik，Peter Filzmoser.Iterative stepwise regression imputation using standard and robust methods ［J］.Computational Statistics and Data Analysis，2011，55 （10）：2793－2806.

［2］SCI2Sthematic public websites.Imputation method ［EB／OL］.［2013－05－05］.http：／／sci2s.ugr.es／MVDM／.

［3］Eduardo R Hruschka，Antonio J T Garcia，Estevam R Hruschka Jr，et al.On the influence of imputation in classification：Practical issues ［J］.Journal of Experimental ＆ Theoretical Artificial Intelligence，2009，21 （1）：43－58.

［4］ZHANG Zhonglin，CAO Zhiyu，LI Yuantao.Research based on euclid distance with weights of k＿means algorithm ［J］.Journal of Zhengzhou University（Engineering Science），2010，31 （1）：89－92 （in Chinese）.［张忠林，曹志宇，李元韬.基于加权欧式距离的k＿means算法研究 ［J］.郑州大学学报，2010，31 （1）：89－92.］

［5］ZHAO Hongbo，JIANG Feng，ZENG Huifen，et al.Rough set approach to data completion based on similarity ［J］.Computer Science，2011，38 （11）：167－171 （in Chinese）.［赵洪波，江峰，曾惠芬，等.一种基于加权相似性的粗糙集数据补齐方法 ［J］.计算机科学，2011，38 （11）：167－171.］

［6］TIAN Shuxin，WU Xiaoping，WANG Hongxia.Improved method for data reinforcement based on ROUSTID ［J］.Journal of Naval University of Engineering，2011，23 （5）：11－15（in Chinese）.［田树新，吴晓平，王红霞.一种基于改进的ROUSTIDA算法的数据补齐方法 ［J］.海军工程大学学报.2011，23 （5）：11－15.］

［7］Rhian M Daniel，Michael G Kenward.A method for increasing the robustness of multiple imputation ［J］.Computational Statistics and Data Analysis，2012，56 （6）：1624－1643.

［8］Zhang Shichao.Nearest neighbor selection for iteratively kNN imputation ［J］.Syst Software，2012，81 （11）：2541－2552.http：／／dx.doi.org／10.1016／j.jss.2012.05.073.

［9］Van Hulse J，Khoshgoftaar T M.Incomplete－case nearest neighbor imputation in software measurement data ［C］／／IEEE International Conference on Information Reuse and Integration，2007：630－637.

［10］Su Yijuan.Multiple imputation method for missing values by gray relation analysis ［J］.Computer Engineering and Appli－cations，2009，45 （15）：169－172.

［11］WANG Guoyin，YAO Yiyu，YU Hong.A survey on rough set theory and application ［J］.Chinese Journal of Computers，2009，32 （7）：1229－1246 （in Chinese）.［王国胤，姚一豫，于洪.粗糙集理论与应用研究综述 ［J］.计算机学报，2009，32 （7）：1229－1246］

［12］LIU Lele，TIAN Weidong.Quantitative association rules mining based on mutual information entropy of attributes ［J］.Computer Engineering，2009，35 （14）：38－40 （in Chinese）.［刘乐乐，田卫东.基于属性互信息熵的量化关联规则挖掘［J］.计算机工程，2009，35 （14）：38－40.］

［13］Yang Yingjie，Robert John.Grey sets and greyness ［J］.Information Science，2012，185 （1）：249－264.