兆瓦级风力机偏航齿圈高强度联接螺栓螺纹表面裂纹扩展分析

李秀珍 ，邓华，吕杏梅，李中林，李润旭

(1. 中南大学 机电工程学院，湖南 长沙，410083；2. 南车株洲电力机车研究所有限公司 风电事业部，湖南 株洲，412001)

高强度联接螺栓是联接兆瓦级风力发电机组偏航系统中重要相关部件的重要元件[1]，其联接的可靠性决定着塔筒与偏航齿圈之间的联接可靠性。而兆瓦级风力机偏航振动过程中的轴向载荷、转矩以及倾覆力矩[2−3]将直接影响高强度联接螺栓联接的可靠性及大型风力发电机组运行的安全性，因此，对兆瓦级风力发电机组偏航齿圈螺栓联接强度进行有效分析和处理显得十分紧迫和重要。传统螺栓联接强度理论[4]往往用来分析螺栓组联接受轴向载荷或倾覆力矩的情况，但其结果却不太令人满意。近年来，德国标准VDI2230工程算法[5]、有限元分析方法或这两者相结合的方法[6−14]等被广泛应用于螺栓联接研究中，Dinger等[8−9]运用VDI2230与有限元相结合分别对螺栓联接的等效刚度与受压模型进行了仿真计算，结果比较理想。对于起联接作用的高强度联接螺栓，由于Schmidt-Neuper法主要适用于塔筒连接处螺栓联接形式，并不适用于塔顶法兰与偏航齿圈处高强度联接螺栓联接形式。而有限元仿真分析法在解决此类问题时具有明显的优势，可在兆瓦级风力发电机组设计初级阶段预先实现对关键零部件进行静强度疲劳分析，并可得到关键零部件如螺栓连接的应力及疲劳寿命。关于兆瓦级风力机高强度联接螺栓螺纹表面裂纹扩展研究目前尚未见相关文献报道，为此，本文作者将有限元仿真分析方法对兆瓦级风力机偏航齿圈高强度联接螺栓螺纹表面裂纹扩展进行仿真分析，这将对解决风力发电机中类似的螺栓联接结构强度静力学性能分析具有一定意义，并可为兆瓦级风力发电机组的稳定运行与可靠性设计提供参考。

1 兆瓦级风力机偏航齿圈高强度联接螺栓螺纹表面裂纹分析仿真模型

1.1 高强度联接螺栓螺纹表面裂纹分析几何模型

在Pro/E中建立几何模型。由于整个兆瓦级风力发电机模型结构复杂，细小零件繁多，为重点分析偏航齿圈与塔架法兰连接处的高强度联接螺栓，对整个模型进行一些合理简化，如：将偏航齿圈上的齿去掉，以圆环的形式替代，其他特征保持不变；将偏航齿圈、塔架法兰、螺栓模型中一些不会对整体分析产生影响的倒角修剪特征及螺栓的螺纹予以删除。Chaib等[15]指出在滚动式偏航轴承螺栓连接内外圈受载后的变形是相互独立的，相对于滑动式只研究偏航齿圈与塔架法兰处的高强度联接螺栓联接，故可将横向吊杆组件予以删除等，具体模型如图1所示。

1.2 高强度联接螺栓螺纹表面裂纹分析有限元模型

由于从整个系统来分析偏航齿圈与塔架法兰处的高强度联接螺栓应力强度，前处理重复步骤繁杂，计算时间较长，且考虑到整个系统结构的几何对称性和最大受载高强度联接螺栓及其极限工况，建立单个高强度联接螺栓联接结构系统的1/88局部模型，模型包括偏航齿圈、塔架法兰的局部模型及与其连接的单个高强度联接螺栓。

图1 偏航齿圈与塔架法兰高强度联接螺栓连接简化模型Fig. 1 Simplified model of bolt connection between yaw gear ring and tower flange

对于预紧力状态下的高强度联接螺栓连接模拟方法主要有：(1) 一维梁单元模拟螺栓，螺纹连接处用MPC连接进行模拟；(2) 实体单元模拟螺栓，螺纹连接处用绑定连接进行模拟。在运用实体单元模拟高强度联接螺栓时，即使不建立详细完整的螺纹细节，其数值仿真结果与实验结果在螺杆部位差别也不大，故可以只建立螺栓头、螺栓杆圆柱体、螺纹啮合部位光杆部分圆柱体来模拟高强度联接螺栓实体单元。

1.2.1 网格划分与单元类型的选取

由于运用 ABAQUS自带的网格划分工具划分模型的网格质量不高，故采用hypermesh来对零件进行六面体单元网格的划分，并在相应部位进行网格加密，单元总数为13 234个，如图2所示。将网格文件导入ABAQUS中选用缩减积分单元 C3D8R，该单元具有较强的接触模拟能力，且相对于协调单元计算成本较低，同样能得到较理想的计算结果。

图2 局部模型网格Fig. 2 Grid of local model

1.2.2 材料属性

塔顶法兰与偏航齿圈材料分别为 Q345E与42CrMo，均为低合金钢，故弹性模量与泊松比分别取为2.1×108Pa与0.3，密度均为7.85 mg/mm3，屈服强度分别为345 MPa与940 MPa。

1.2.3 接触、加载与边界条件的确定

模型中主要包括 4对接触面：(1) 螺栓头端面与垫圈；(2) 垫圈与法兰面；(3) 法兰与偏航齿圈接触面；(4)螺栓螺纹与偏航齿圈内螺纹孔。前3对接触面均为面面接触(surface-to-surface contact)，摩擦因数设为0.15。对于接触面(4)，为了增加计算收敛性，将其设为绑定接触，控制螺纹接触区域的相对位移。

载荷边界的施加分3步：首先，用bolt load对高强度联接螺栓施以预紧力537 kN；其次，在第2个分析步中施加极限载荷，如表2所示(其中极限载荷根据表 1换算所得)；最后，对局部模型在参考点(与法兰上端面耦合)上施以如图3所示的等效力。

模型的约束边界条件设置如下：限制塔架法兰塔筒壁下端面的3个自由度。由于此模型为单个高强度联接螺栓联接结构系统的1/88局部模型，为了等效于一个实际完整的系统模型，应对此局部模型施以循环对称约束。

1.2.4 有限元计算方法

本文模型采用的空间单元为八节点六面体单元。其单元节点列阵为

在单元中心建立一个局部坐标系(ξ,η,ζ)，其中，ξ，η和ζ轴分别与x,y和z轴平行，则节点的位移函数可表示为

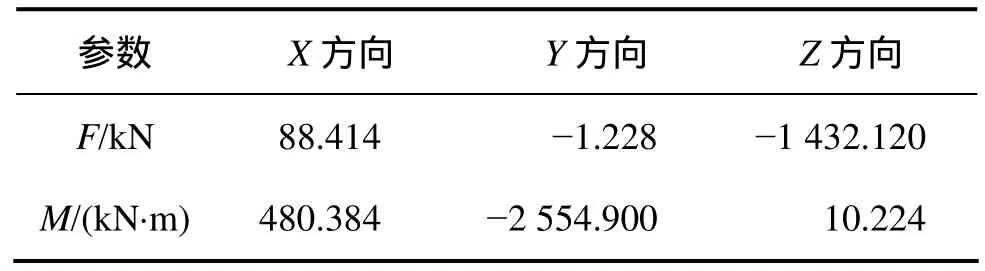
表1 整个模型的极限载荷Table 1 Limit load of whole model

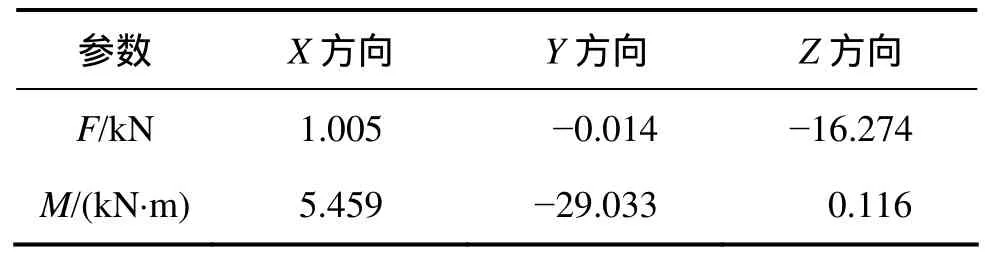
表2 局部模型等效极限载荷Table 2 Equivalent limit load of local model

图3 极限载荷在参考点RB1的耦合Fig. 3 Coupling of limit load at the reference point RB1

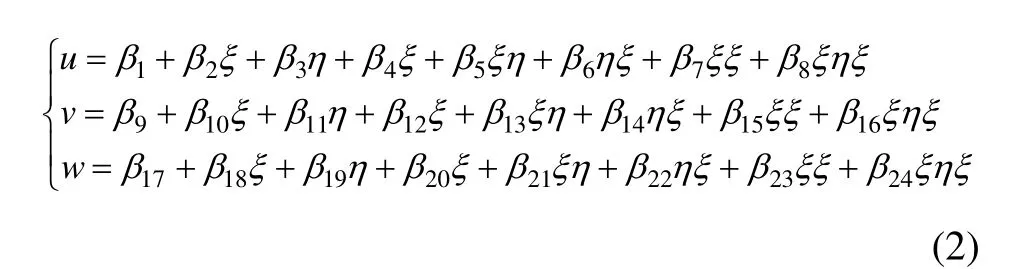
单元位移和节点位移之间的关系为

式中：{f}为单元内位移函数列阵；为单元节点位移列阵；[N]为形函数矩阵。各形函数可由形函数的性质确定，最终可表示为

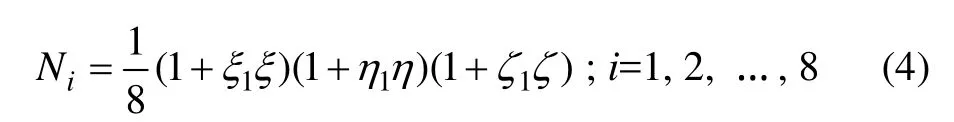
单元刚度矩阵为

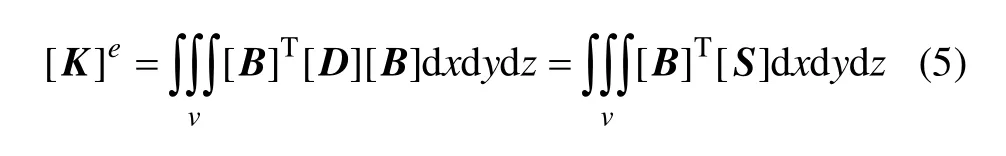
式中：[B]为单元的几何矩阵；[D]为单元的弹性模量矩阵。

单元等效节点力为

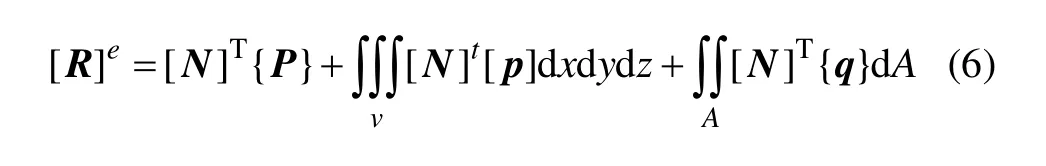
式中：右端第1项为节点上集中力移置的等效节点力；第2项为单元的分布体力等效节点荷载；第3项为单元的分布面力移置的等效节点荷载。

根据李振强的研究结果[16]和最大拉应力理论，提出以下 2个假设：(1) 假设裂纹是沿最大拉应力方向发生临界扩展；(2) 假设裂纹扩展是由于周向拉应力的最大值达到临界值时产生的。裂纹模型示意图如图4所示，有

式中：σ为裂纹处最大应力；a为裂纹深度；b为裂纹长度；F为关联函数；D为螺栓直径；Φ为裂纹上某一点与裂纹深度方向的夹角。

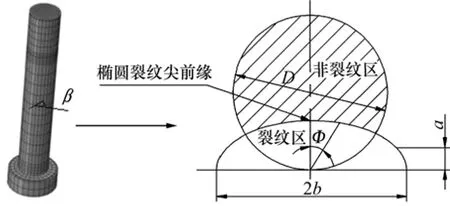
图4 裂纹模型示意图Fig. 4 Schematic diagram of crack model

2 高强度联接螺栓螺纹表面裂纹仿真计算分析

根据实际应用经验，螺纹处表面裂纹扩展情况可分为以下2类：(1)螺纹底端表面裂纹；②螺纹顶端表面裂纹。令裂纹深度c分别为1，2和3 mm，裂纹长度d为螺距4 mm。裂纹方向为半径方向，且在螺纹第1个螺纹处、中间第3个螺纹处及底端倒数第2个螺纹处对高强度联接螺栓螺纹3个不同位置进行裂纹扩展分析。

2.1 螺纹底端表面裂纹

2.1.1c=1 mm时的裂纹扩展

当裂纹深度c=1 mm时，裂纹扩展有限元分析模型及结果如图5所示。从图5可见：不论初始裂纹设置在哪个位置，高强度联接螺栓最大应力与无裂纹时一样，出现在高强度联接螺栓的第1个螺纹处。

当初始裂纹设置在第1个螺纹处时，经裂纹扩展后，裂纹处最大单元应力即高强度联接螺栓最大应力，为833.3 MPa，应力安全系数为SF=940/833.3 =1.13，未超出其材料屈服极限，符合强度要求；

当初始裂纹分别设置在中间第3个螺纹处底端和倒数第2个螺纹处底端时，经裂纹扩展后，裂纹处最大单元应力分别为494.835 MPa和85.750 MPa，高强度联接螺栓最大应力均为765.1 MPa，应力安全系数为SF=940/765.1=1.22，未超出其材料屈服极限，符合强度要求。

2.1.2c=2 mm时的裂纹扩展

当裂纹深度c=2 mm时，裂纹扩展有限元分析模型及结果如图6所示。从图6可见：不论初始裂纹设置在哪个位置，高强度联接螺栓最大应力仍然出现在高强度联接螺栓的第1个螺纹处。

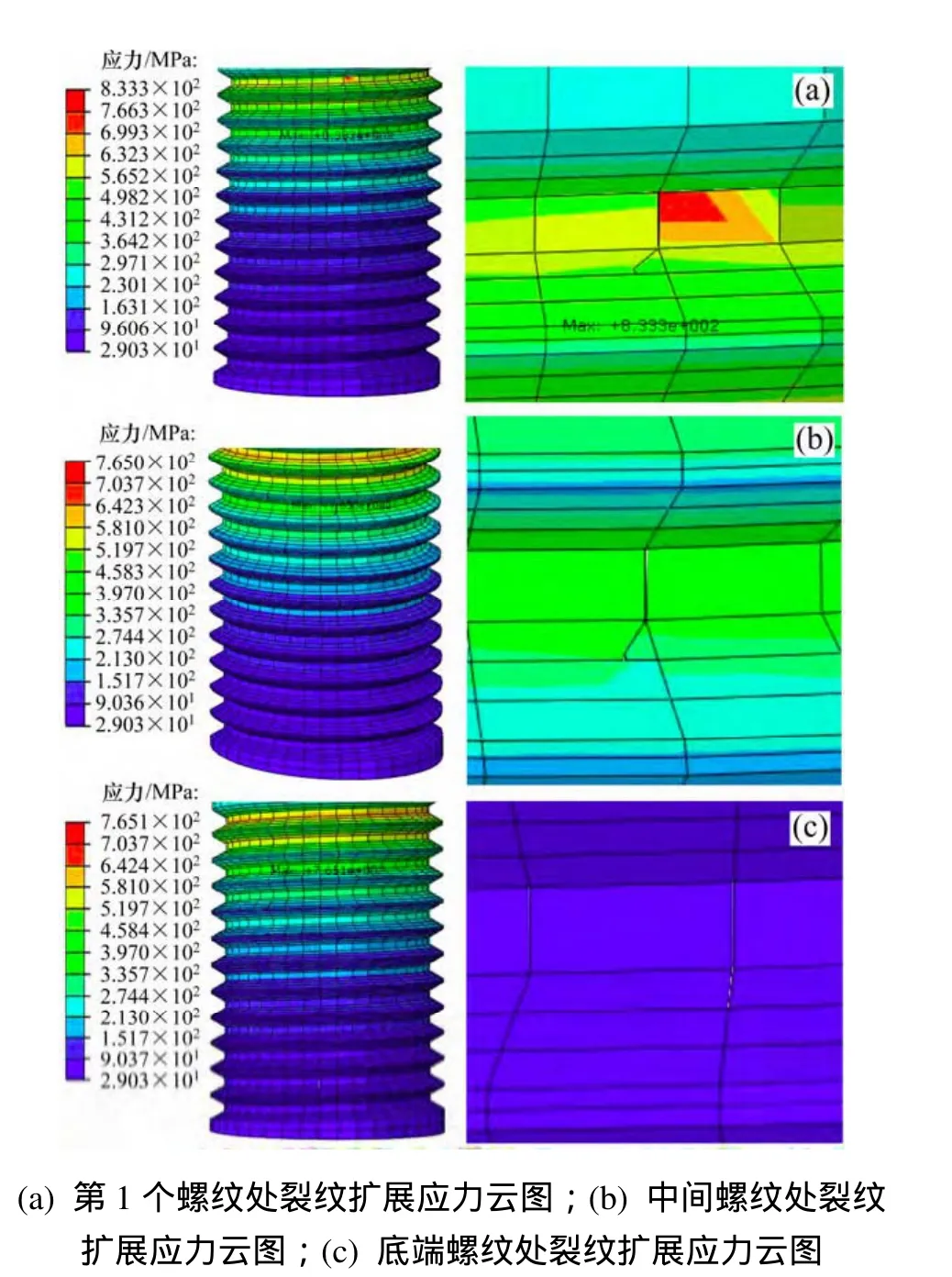
图5 c=1 mm时螺纹底端表面裂纹情况Fig. 5 Surface crack at bottom of thread when c=1 mm

图6 c=2 mm时螺纹底端表面裂纹情况Fig. 6 Surface crack at bottom of thread when c=2 mm

当初始裂纹设置在第1个螺纹处时，经裂纹扩展后，裂纹处最大单元应力即高强度联接螺栓最大应力，为881.1 MPa，应力安全系数为SF=940/881.1=1.07。虽然安全系数未超出其材料屈服极限，但由于应力安全系数过小，故此类裂纹不能出现，否则，将导致高强度联接螺栓联接不可靠，进而影响整个风机的安全运转；

当初始裂纹分别设置在中间第3个螺纹处底端和倒数第2个螺纹处时，经裂纹扩展后，裂纹处最大单元应力分别为508.284 MPa和92.1676 MPa，高强度联接螺栓最大应力均为 765.1 MPa，应力安全系数为SF=940/765.1=1.22，未超出其材料屈服极限，符合强度要求。

2.1.3c=3 mm时的裂纹扩展

当裂纹深度c=3 mm时，裂纹扩展有限元分析模型及结果如图7所示。从图7可见：不论初始裂纹设置在哪个位置，高强度联接螺栓最大应力仍然出现在高强度联接螺栓的第1个螺纹处。

当初始裂纹设置在第1个螺纹处时，经裂纹扩展后，裂纹处最大单元应力即高强度联接螺栓最大应力，为896.2 MPa，应力安全系数为SF=940/896.2=1.04，虽然未超出其材料屈服极限，但由于应力安全系数过小，故此类裂纹不能出现，否则，将导致高强度联接螺栓联接不可靠，进而影响整个风机的安全运转。

当初始裂纹分别设置在中间第3个螺纹和倒数第2个螺纹处底端时，经裂纹扩展后，裂纹处最大单元应力分别为510.063 MPa和93.141 MPa，高强度联接螺栓最大应力均为 765.1 MPa，应力安全系数为SF=940/765.1=1.22，未超出其材料屈服极限，符合强度要求。

螺纹底端表面不同裂纹条件下裂纹最大单元应力p1与高强度联接螺栓最大应力p2的差异的比较如表3所示。

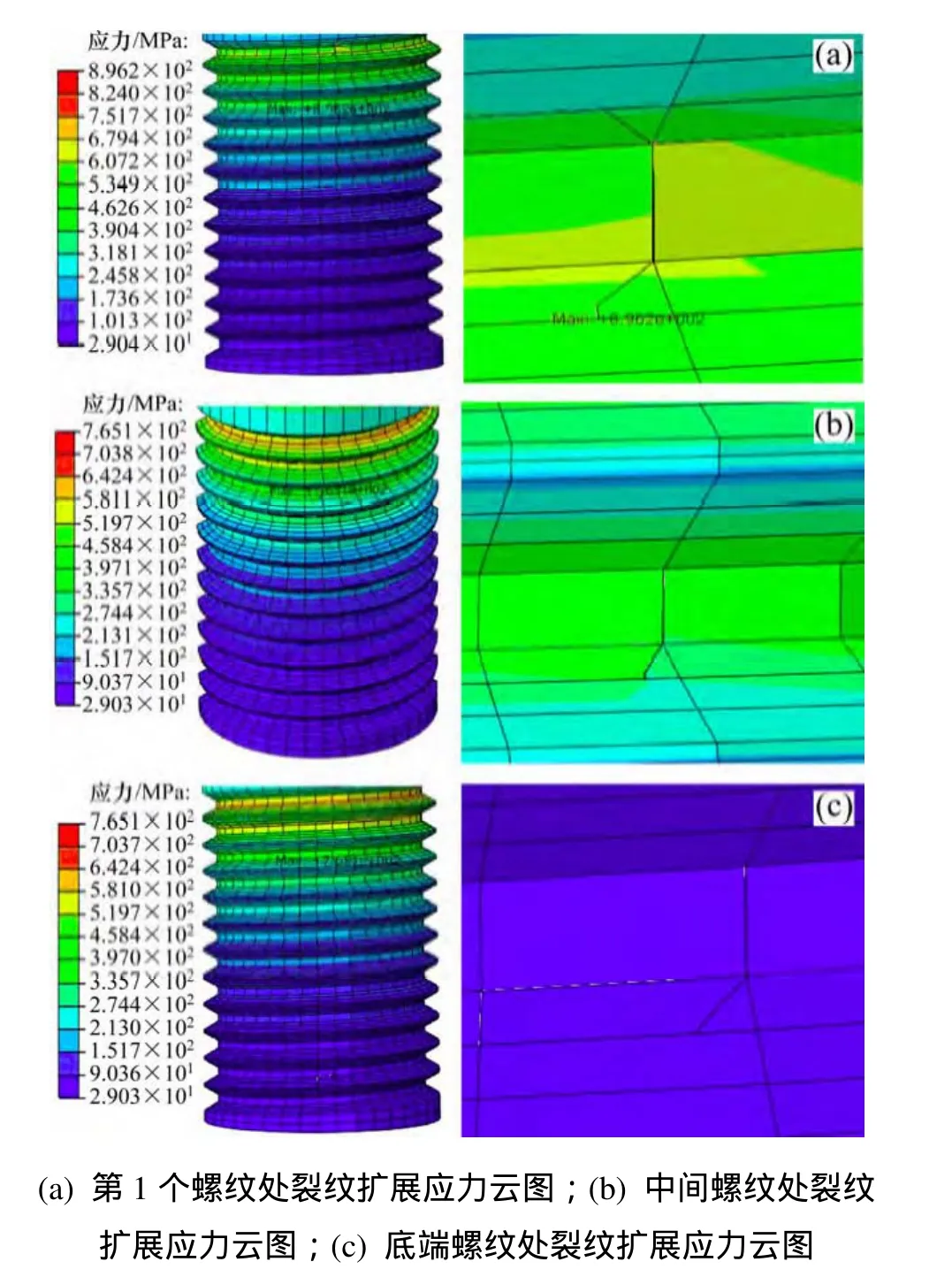
图7 c=3 mm时螺纹底端表面裂纹情况Fig. 7 Surface crack at bottom of thread when c=3 mm

综上所述，高强度联接螺栓最大应力位置与裂纹位置无关，均出现在螺纹连接第1个螺纹处，且随着裂纹深度的不断增加，高强度联接螺栓裂纹处最大单元应力也不断增大，特别是在初始裂纹设置在第1个螺纹处时，由于高强度联接螺栓联接结构裂纹处产生应力集中、发生裂纹扩展现象，导致高强度联接螺栓应力过大。

2.2 螺纹顶端表面裂纹

2.2.1c=1 mm时的裂纹扩展

当裂纹深度c=1 mm时，裂纹扩展有限元分析模型及结果如图8所示。从图8可见：与裂纹初始位置在螺纹底端一样，出现在高强度联接螺栓的第1个螺纹处。

表3 螺纹底端表面不同裂纹条件下应力对比Table 3 Stress comparison at different conditions of thread bottom surface crack MPa

图8 c=1 mm时螺纹顶端表面裂纹情况Fig. 8 Surface crack at top of thread when c=1 mm

当初始裂纹设置在第1个螺纹处时，经裂纹扩展后，螺牙沿裂纹错位开裂，裂纹处最大单元应力即高强度联接螺栓最大应力，为 908.2 MPa，应力安全系数为SF=940/908.2=1.03，虽然未超出其材料屈服极限，但由于应力安全系数过小，故此类裂纹不能出现，否则，将严重影响整个风机的联接可靠性。

当初始裂纹分别设置在中间第3个螺纹处和倒数第2个螺纹处顶端时，经裂纹扩展后，裂纹处最大单元应力分别为737.721 MPa和91.591 MPa，高强度联接螺栓最大应力均为 765.2 MPa，应力安全系数为SF=940/765.2=1.22，未超出其材料屈服极限，符合强度要求。

2.2.2c=2 mm时的裂纹扩展

当裂纹深度c=2 mm时，裂纹扩展有限元分析模型及结果如图9所示。从图9可同见：最大应力位置与裂纹初始位置无关，出现在高强度联接螺栓的第 1个螺纹处。

当初始裂纹设置在第1个螺纹处时，经裂纹扩展后，螺牙沿裂纹错位开裂，裂纹处最大单元应力即高强度联接螺栓最大应力，为 763.5 MPa，应力安全系数为SF= 940/763.5=1.22，未超出其材料屈服极限，符合强度要求。

当初始裂纹分别设置在中间第3个螺纹处和倒数第2个螺纹处顶端时，经裂纹扩展后，裂纹处最大单元应力分别为737.721 MPa和91.591 MPa，高强度联接螺栓最大应力均为 765.1 MPa，应力安全系数为SF=940/765.1=1.22，未超出其材料屈服极限，符合强度要求。

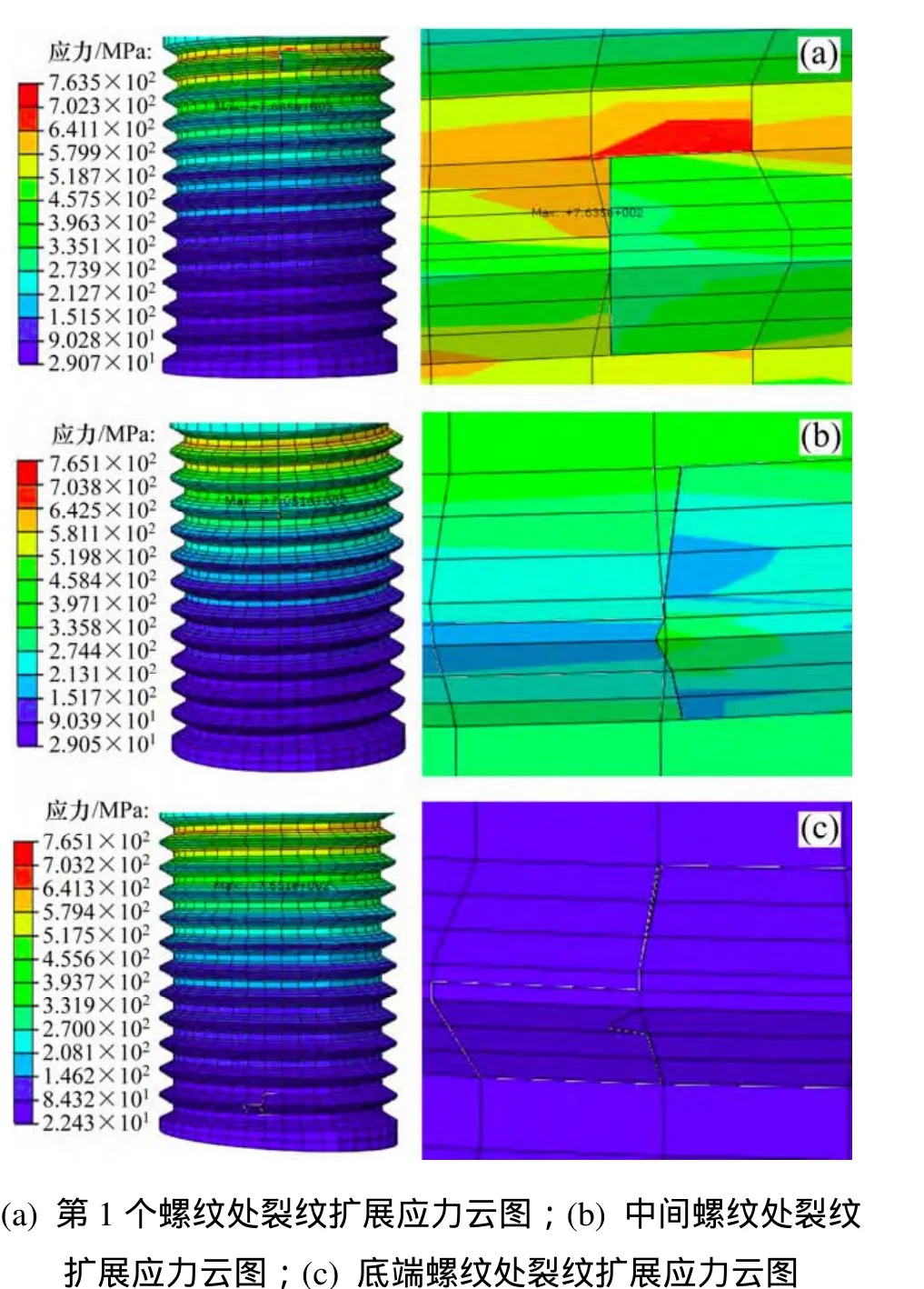
图9 c=2 mm时螺纹顶端表面裂纹情况Fig. 9 Surface crack at top of thread when c=2 mm

2.2.3c=3 mm时的裂纹扩展

当裂纹深度c=3 mm时，裂纹扩展有限元分析结果如图10所示。从图10可见：最大应力位置同样与裂纹初始位置无关，出现在高强度联接螺栓的第1个螺纹处。

当初始裂纹设置在第1个螺纹处时，经裂纹扩展后，螺牙沿裂纹错位开裂，裂纹处最大单元应力即高强度联接螺栓最大应力，为 767.2 MPa，应力安全系数为SF=940/767.2=1.22，未超出其材料屈服极限，符合强度要求。

当初始裂纹分别设置在中间第3个螺纹处和倒数第2个螺纹处顶端时，经裂纹扩展后，裂纹处最大单元应力分别为538.289 MPa和85.187 MPa，高强度联接螺栓最大应力均为 765.1 MPa，应力安全系数为SF=940/765.1=1.22，未超出其材料屈服极限，符合强度要求。

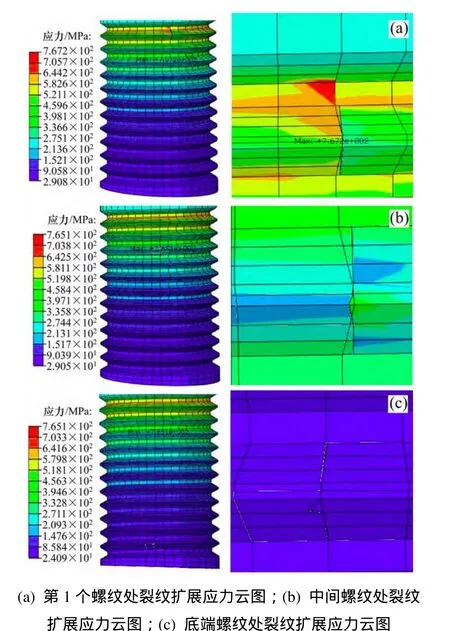
图10 c=3 mm时螺纹顶端表面裂纹情况Fig. 10 Surface crack at top of thread when c=3 mm

螺纹顶端表面不同裂纹条件下裂纹最大单元应力(p1)与高强度联接螺栓最大应力(p2)的差异比较如表 4所示。

综上所述，高强度联接螺栓最大应力位置同样与裂纹位置无关，均出现在螺纹连接第1个螺纹处。

3 结论

(1) 考虑到整个系统结构的几何对称性和最大受载螺栓及其极限工况，建立单个高强度联接螺栓联接结构系统的1/88局部模型；按照不同裂纹深度c和不同裂纹长度对高强度联接螺栓螺纹底端表面裂纹和螺纹顶端表面裂纹的扩展情况进行了有限元仿真分析，为存在裂纹缺陷的高强度联接螺栓二次使用提供了理论依据。

(2) 对于存在螺纹底端表面裂纹缺陷和螺纹顶端表面裂纹缺陷的高强度联接螺栓，最大应力位置与裂纹位置无关，均出现在螺纹连接的第1个螺纹处；随着裂纹深度的不断增加，高强度联接螺栓裂纹处最大单元应力也不断增大，特别是在初始裂纹设置在第 1个螺纹处时，由于高强度联接螺栓联接结构裂纹处产生应力集中、发生裂纹扩展现象，导致高强度联接螺栓应力过大，严重影响连接可靠性，故应特别注意此类裂纹，防止其出现。

(3) 对于存在螺纹顶端表面裂纹缺陷的高强度联接螺栓，高强度联接螺栓最大应力位置同样与裂纹位置无关，均出现在螺纹连接第1个螺纹处，特别是在初始裂纹设置在第1个螺纹处时，由于高强度联接螺栓联接结构裂纹处产生应力集中、发生裂纹扩展现象，导致高强度联接螺栓应力或螺牙应变过大，严重影响连接可靠性，故应特别注意此类裂纹，防止其出现。

表4 螺纹顶端表面不同裂纹条件下应力对比Table 4 Stress comparison at different conditions of thread top surface crack MPa

[1]赵海川, 黄海江. 风电行业高强螺栓的润滑问题分析[J]. 风能, 2010(4): 64−66.ZHAO Haichuan, HUANG Haijiang. Lubrication analysis for high-strength bolts of wind power industry[J]. Wind Energy,2010(4): 64−66.

[2]陈真. 风力发电机组高强度联接螺栓连接技术研究[D]. 重庆:重庆大学, 2011: 43−51.CHEN Zhen. Study of high strength bolt jointon wind turbine[D].Chongqing:Chongqing University,2011: 43−51.

[3]Göncz P, Glodež S. Calculation model for pre-stressed bolted joints of slewing bearings[J]. Advanced Engineering, 2009, 3(2):175−186.

[4]成大先. 机械设计手册(单行本)联接与紧固[M]. 北京: 化学工业出版社, 2004: 9−11.CHENG Daxian. Standard handbook of machine design (booklet)join and fastening[M]. Beijing: Chemical Industry Press, 2004:9−11.

[5]VDI2230 Part 1, Systematic calculation of high duty bolted joints, joints with one cylindrical bolt[S].

[6]HUANG Yonghui. Finite element analysis and experimental study on high strength bolted friction grip connections in steel bridges[J]. Journal of Constructional Steel Research, 2010, 6(66):803−815.

[7]Lee S H, Kim J H, Choi S M. Structural behavior of tension joint with high-strength bolted split-tee[J]. International Journal of Steel Structures, 2009, 9(2): 93−105.

[8]Dinger G, Friedrich C. Avoiding self-loosening failure of bolted joints with numerical assessment of local contact state[J].Engineering Failure Analysis, 2011, 18(8): 2188−2200.

[9]Naruse T, Shibutani Y. Equivalent stiffness evaluations of clamped plates in bolted joints under loading[J]. Journal of Solid Mechanics and Materials Engineering, 2010, 4(12): 1791−1805.

[10]Chakhari J, Daidié A, et al. Numerical model for two-bolted joints subjected to compressive loading[J]. Finite Elements in Analysis and Design, 2008, 44(4): 162−173.

[11]严晓林, 刘希凤. 基于ABAQUS的风力机塔筒螺栓连接接触非线性分析[J]. 科学技术与工程, 2011, 11(28): 6842−6845.YAN Xiaolin, LIU Xifeng. Contact nonlinear analysis of wind turbine tower bolted joints with ABAQUS[J]. Science Technology and Engineering, 2011, 11(28): 6842−6845.

[12]陈真, 杜静, 何玉林, 等. 采用VDI2230的风力发电机组塔筒法兰联接处螺栓强度分析[J]. 现代制造工程, 2011(5):125−129.CHEN Zhen, DU Jing, HE Yulin, et al. Strength analysis of bolt joint on wind turbine tower flange based on VDI2230[J].Modern Manufacturing Engineering, 2011(5): 125−129.

[13]李曼, 王林, 王广庆, 等. 风力发电机组高强度连接螺栓的计算方法[J]. 机械制造与自动化, 2012, 41(1): 176−177.LI Man, WANG Lin, WANG Guangqing, et al. High-strength bolt calculation of wing turbine[J]. Machine Building ＆ Automation, 2012, 41(1): 176−177.

[14]Croccolo D, de Agostinis M, Vincenzi N. A contribution to the selection and calculation of screws in high duty bolted joints[J].International Journal of Pressure Vessels and Piping, 2012, 96:38−48.

[15]Chaib Z, Daidie A, Leray D. Screw behavior in large diameter slewing bearing assemblies: Numerical and experimental analyses[J]. International Journal on Interactive Design and Manufacturing, 2007, 1(1): 21−31.

[16]李振强. 兆瓦级风力发电机高强度螺栓联接静力学性能分析[D]. 长沙: 湖南大学, 2013.LI Zhenqiang. Static analysis of high strength bolt connection on the MW wind turbine generator system[D]. Changsha: Hunan University, 2013.