基于路径估计的卫星双向传播时延差估算方法

杨文可，占建伟，龚航，朱祥维，孙广富

(国防科学技术大学 电子科学与工程学院，湖南 长沙，410073)

采用静地轨道(GEO)卫星的卫星双向时间频率传递(TWSTFT)是国际上最重要的实现远程时间比对的方法之一，而包括地球自转效应(Sagnac效应)修正、电离层时延差、对流层时延差等在内的双向空间传播时延差是造成 TWSTFT所测量的钟差存在偏差的主要因素[1]。实际上，由于各种摄动力的存在[2]，GEO卫星相对于地面站存在相对运动。国际权度局(BIPM)给出的TWSTFT数据处理指导[1]以理想GEO卫星为基础，给出了计算Sagnac效应修正量、电离层时延差的方法，该方法是国际上一般处理TWSTFT数据的方法，本文简称其为BIPM法。虽然其中提到了卫星运动对双向Sagnac效应修正量、双向几何距离时延差的影响量级，但未给出估算方法。研究卫星运动对TWSTFT影响的文献中，一般只分析了卫星运动对 Sagnac效应修正量的影响[3−6]及双向几何距离差[3−4,7−8]，而忽略了卫星运动对电离层时延差、对流层时延差的影响。其中，Sagnac效应修正量的分析一般以BIPM法中的Sagnac效应修正公式为基础[3,5−6]；分析双向几何距离差时，一般是以两地面站与卫星之间的距离差除以光速估算得到地面站信号到达卫星的时差，再结合卫星速度进行估算[7−8]。以上分析方法未考虑信号真实传播路径，未综合考虑信号传播方向上经历的Sagnac效应、几何路径时延、电离层时延、对流层时延等，并且一般以模型[3]或精度为几十千米的轨道数据[4,8]来描述卫星运动，存在误差。在北斗导航系统中，基于GEO导航卫星的TWSTFT实现站间时间同步[9]，且该GEO卫星具有2 h拟合精度好于0.1 m、径向误差为厘米量级的广播星历[10]。不同于前述文献所提方法，本文作者以广播星历数据为依托，对卫星或地面站的坐标进行旋转来修正Sagnac效应，获知真实信号传播路径，并综合考虑几何路径时延、电离层时延修正、对流层时延修正等对卫星与地面站之间的单向空间传播时延建模，提出一种利用迭代法分别计算上行、下行信号时延，并精确计算TWSTFT中双向空间传播时延差的方法。

1 卫星双向时延模型

当考虑卫星相对于地面站的相对运动时，卫星双向时间频率传递的时延模型如图1所示。

图1中，τUi为地面站i(i=1, 2)到卫星的上行信号空间传播时延，包含4部分：由地面站i到卫星的伪几何距离时延τUi|SatP、地球自转效应(Sagnac效应)时延修正τSCUi、电离层时延修正τUi|Ion、对流层时延修正τUi|Trop；τDi为卫星到地面站i的下行信号空间传播时延，也包含4部分：由卫星到地面站i的伪几何距离时延τDi|SatP、Sagnac效应时延修正τSCDi、电离层时延修正τDi|Ion、对流层时延修正τDi|Trop；τTi和τRi分别为地面站i发射信号时延和接收信号时延；τSij(i=1, 2,j=1, 2,i≠j)为卫星由地面站i向地面站j转发信号时延。

其中，之所以称τUi|SatP和τDi|SatP为伪几何距离时延，是由于该几何距离时延未考虑 Sagnac效应的影响，不同于将伪几何距离时延经过Sagnac效应修正得到的地面站到卫星(或卫星到地面站)真实传播几何路径时延，记为τUi|Sat(或τDi|Sat)。

图1 卫星双向时间频率传递的时延模型示意图Fig. 1 Schematic diagram of two-way satellite time and frequency transfer with satellite in motion

当记以钟i为参考测量所得的地面站j的信号时延为PRij(i=1, 2，j=1, 2，i≠j)时，钟1与钟2之间的时差，记为T1−T2，可表示为[1]：

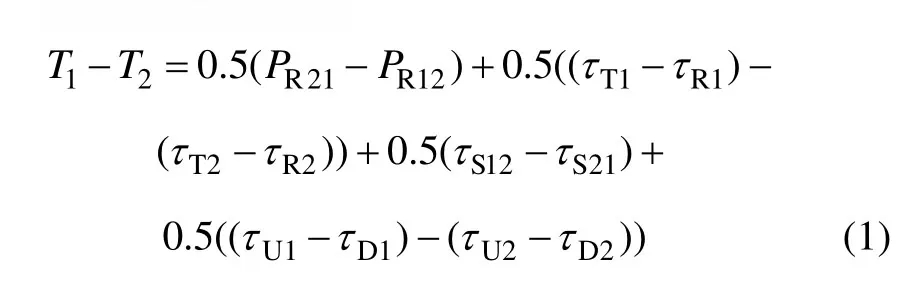
式中：0.5((τT1−τR1)−(τT2−τR2))为双向地面站发射时延与接收时延差；0.5(τS12−τS21)为双向卫星转发时延差，这两者可通过标定获得[1,11]。因此，为精确计算双向时延差，即式(1)等式右边除双向测量时差0.5(PR21−PR12)以外，还需确定双向空间传播时延差 0.5((τU1−τD1)−(τU2−τD2))，记为τUD，且可分解为

2 算法原理

对下行或上行信号传播时延的估算是一个基于信号路径估计的迭代计算的过程，基本流程如图2所示。

图2 单向信号传播时延迭代计算流程Fig. 2 One-way signal propagation delay iterative calculation flow

2.1 下行信号传播时延模型

如图1所示，以卫星到地面站1的下行链路为例，下行信号时延τDn1，可表示为

其中，地面站1信号接收时延可通过标校获得[11]。以下分析除τR1以外的时延计算模型，即

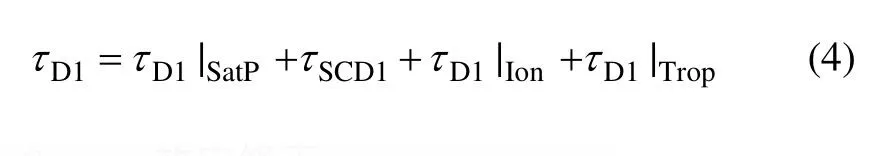
2.1.1 Sagnac效应修正

在式(2)中对下行信号时延的 Sagnac效应的修正是以时延修正量τSCD1的方式表示的。然而，本质上，下行信号时延的 Sagnac效应修正是为了获得卫星到地面站方向的信号传播路径。为此，本文对卫星位置坐标进行修正，获得信号实际传播路径，具体过程如下。

(1) 假设下行信号时延为τDn1，地面站1接收信号时刻为tr1，则可知卫星转发信号时刻ttr21为

(2) 对卫星广播星历进行插值，获得在ttr21时刻的地心地固(ECEF)坐标系下卫星位置{xs,ys,zs}，记为S；

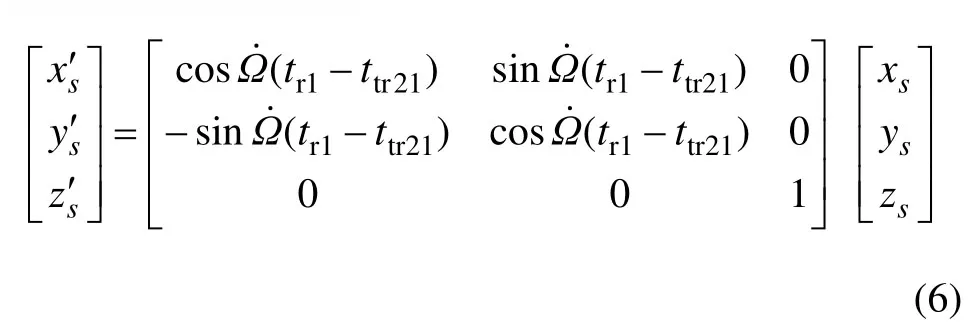
(4) 地面站1在tr1的ECEF坐标系下的坐标{x1,y1,z1}，记为GS1，与卫星位置S′之间的连线方向是实际信号传播路径。其中，GS1为已知量。另外，据式(6)，S′由tr1，ttr21和S共同决定。已知tr1，同时，当星历已知时，S实际上由ttr21决定。由此，S′是ttr21的函数，且τR1已知，则据式(5)和式(4)可知S′实际上是τD1的函数，记为

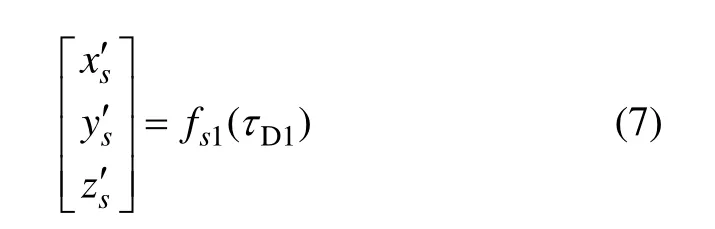
2.1.2 几何距离时延

当经过 Sagnac效应修正后，伪几何距离时延τD1|SatP修正为几何距离时延τD1|Sat，即

其中：c为光在真空中传播的速度，为299 792 458 m/s。

可见：几何距离时延τD1|Sat是地面站1坐标GS1与经 Sagnac效应修正的转发信号时刻卫星坐标S′的函数。若隐去已知量，结合式(7)，则τD1|Sat也可简记为τD1的函数：

2.1.3 电离层时延修正

由于电离层折射引起的伪码相位时延修正量τD1|Ion可写为[1]

其中：s为倾斜因子，由信号传播路径决定，是经Sagnac效应修正的转发信号时刻ttr21卫星坐标S′和地面站 1坐标GS1的函数；TEC为地面站1顶端垂直方向上总电子数，可采用IGS提供的电离层网格参数[13]进行时间和空间上的线性插值计算得到，是卫星转发信号时刻ttr21和地面站1坐标GS1的函数；fd为下行信号载波频率，为已知量。

若隐去已知量，结合式(6)，则τD1|Ion同样可简记为τD1的函数：

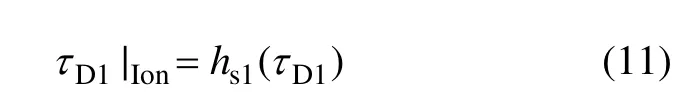
2.1.4 对流层时延修正

对流层时延修正模型有多种，本文使用 Collins模型，则τD1|Trop可写为[14]

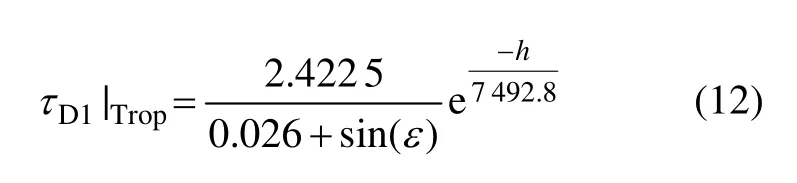
其中：h为地面站1高度；ε为地面站1对卫星的仰角。

由于地面站1高度h可由其ECEF坐标GS1转换得到，地面站1对卫星仰角ε是GS1和S′的函数。则隐去已知量，结合式(7)，τD1|Trop可简写为

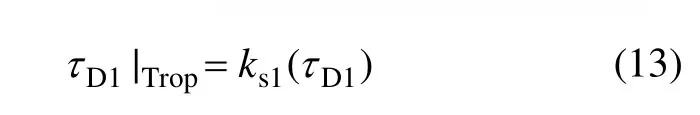
2.2 上行信号空间传播时延

仍以地面站2到卫星到地面站1的链路为例，说明当计算得到卫星到地面站1的下行信号空间传播时延τD1后，如何计算地面站 2到卫星的上行信号空间传播时延，记为τU2。

上行信号时延τUp2为

其中，地面站2信号发送时延可通过标校获得[11]。以下，分析除τT2以外的时延计算模型，即

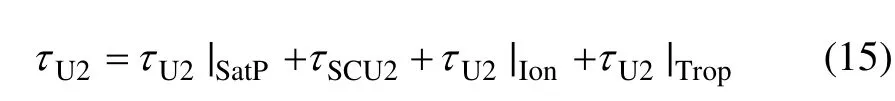
当忽略卫星转发信号时延，及期间的卫星位置改变，认为卫星转发信号时刻的位置即为卫星接收信号时刻的位置，则已知卫星转发信号时刻ttr21和该时刻ECEF坐标系下的坐标为S，则可按照类似下行单向时延的模型对上行单向时延进行建模。

区别仅在于，修正Sagnac效应时，需修正地面站2(信号发射方)的位置，获知信号实际传播路径，其过程如下。

(1) 已知卫星转发信号时刻ttr21，则可知地面站2发射信号时刻tt2为：

(2) 地球旋转速率设为，将tt2时刻地面站2在ECEF坐标系下的坐标{x2,y2,z2}，记为GS2，修正至卫星转发信号时刻ttr21的ECEF坐标系下坐标}，记为：

(3) 卫星转发信号时刻ttr21的ECEF坐标系下地面站2的坐标到卫星位置坐标S之间的连线方向为实际信号传播路径。其中，据式(21)，由ttr21，tt2和GS2共同决定。而GS2为已知量，ttr21已知，tt2由τUp2和ttr21共同决定。隐去已知量，GS2 ′实际上是τU2的函数。

按照类似于下行单向时延的建模和推导过程，可得到：

其中：

即上行信号几何距离时延τU2|Sat，电离层时延修正τU2|Ion，对流层时延修正τU2|Trop都是τU2的函数。

2.3 迭代法计算

将式(9)，(11)，(13)代入式(4)，得到：

另外，式(23)与式(21)具有类似的形式，可通过迭代法[15]求等式(21)和(23)的解τD1和τU2。以求解式(21)的解τD1的过程进行说明：

(1) 设定初始解τD1(0)=130 ms：

(2) 第j(j≥1)次迭代计算过程如下：

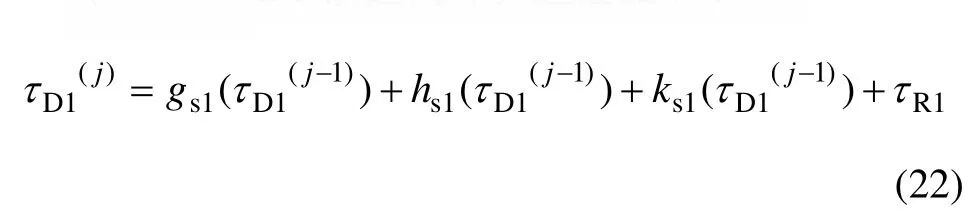
(3) 设置门限λ(λ＞0)，收敛条件为：

其中，门限选取为时延有效数据位量级的1/10。若有效数据位量级为1 ps，则λ=0.1 ps。

(4) 当满足式(16)的收敛条件时，停止迭代计算，则

当计算得到地面站2到卫星再到地面站1以及地面站1到卫星再到地面站2的双向链路的下行单向时延τDn1和τDn2以及上行单向时延τUp1和τUp2时，可求得双向空间传播时延差τUD。

3 实验结果

本文以北斗导航系统中相距3 376 km的地面站1、地面站2之间通过位于东经140°的GEO卫星建立的C波段TWSTFT链路的2 d实测数据为例，采用本文方法和BIPM法计算双向传播时延差，并分析两者的差异。

图3所示为GEO卫星的星下点轨迹。由图3可见：GEO卫星的星下点轨迹具有以d为单位的周期波动(以下简称日波动)，经度变化幅度为0.09°，纬度变化幅度为3.18°。

图3 GEO卫星的星下点轨迹Fig. 3 Sub-satellite point track of GEO satellite

双向几何距离时延差τUD|Sat包含伪几何距离时延差τUD|SatP和Sagnac效应修正量τUD|SC。如图4所示，使用BIPM法，即认为GEO卫星相对地面站无相对运动时，τUD|Sat为定值−84.149 ns；使用本文方法，即考虑卫星运动以及信号传播路径时，发现τUD|Sat呈现幅度为0.412 ns的日波动，均值为−84.266 ns，与BIPM法结果偏差77 ps。

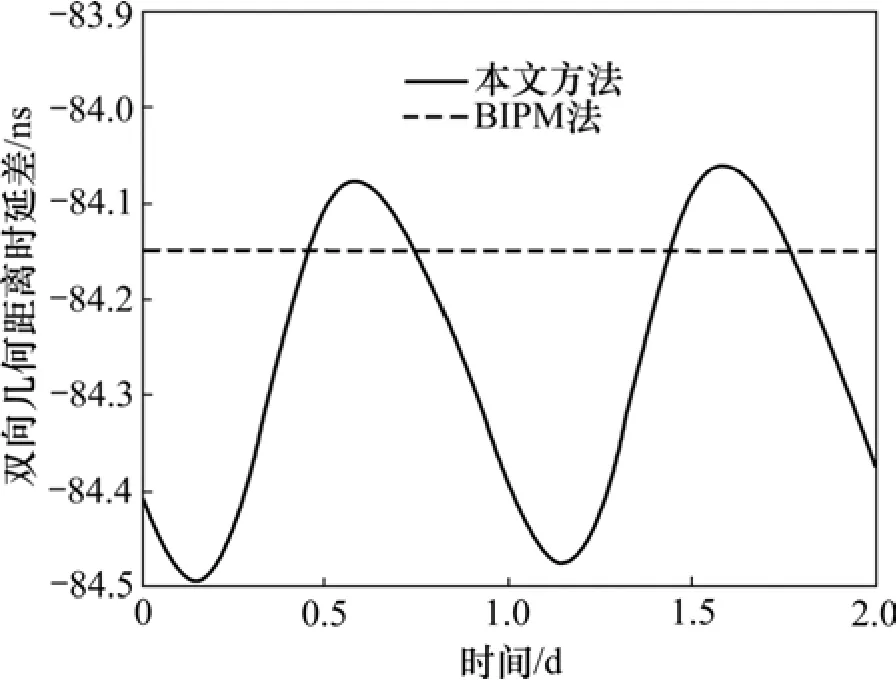
图4 双向几何距离时延差(包含双向Sagnac效应修正)τUD|SatFig. 4 Two-way geometry signal path difference (including two-way Sagnac effect correction) τUD|Sat

图5 双向电离层时延的双差(本文方法与BIPM法计算所得双向电离层时延差τUD|Ion 的差值)Fig. 5 Double difference of two-way ionospheric corrections(the difference of two-way ionospheric correction differenceτUD| Ion calculated by method introduced in this work and BIPM method)

图 5所示为本文方法计算得双向电离层时延差τUD|Ion与BIPM法计算得双向电离层时延差τUD|Ion的差值。由于卫星运动造成地面站到卫星，以及卫星到地面站的双向信号路径改变，使得双向电离层时延修正量较卫星相对地面站静止的情况有所改变。并且，由于电离层电子浓度在白天较大，在夜晚较小，使得该差值呈现日波动，且幅值白天较大，夜晚较小，最大幅度为0.120 ns，均值为31 ps。

双向对流差时延差如图6所示。从图6可见：当不考虑卫星相对地面站运动时(BIPM法)，双向对流层时延差τUD|Trop几乎为0；使用本文方法计算，发现D|Trop也呈现日波动，幅度为0.3 ps，均值为−0.9 ps。

同时考虑τUD|Sat，τUD|Ion和τUD|Trop，得到卫星双向传播时延差τUD。卫星双向传播时延的双差(本文方法与 BIPM 法计算所得卫星双向传播时延差τUD的差值)如图 7所示。从图 7可见：对比本文方法结果与BIPM 法结果，卫星星下点轨迹的日波动引入了τUD幅度为0.406 ns，均值为−0.087 ns的日波动。

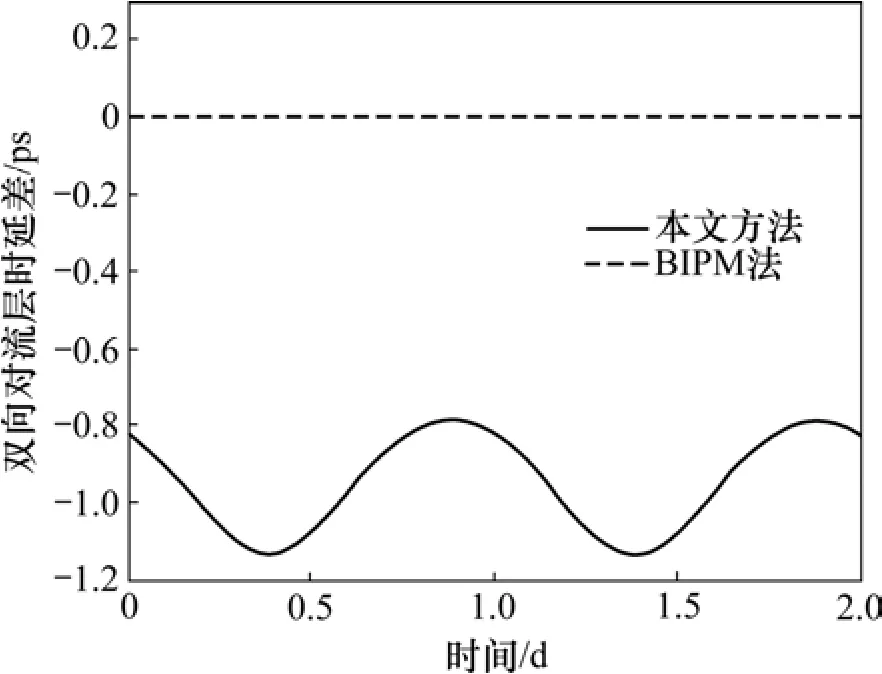
图6 双向对流层时延差τUD|TropFig. 6 Two-way tropospheric correction difference τUD| Trop

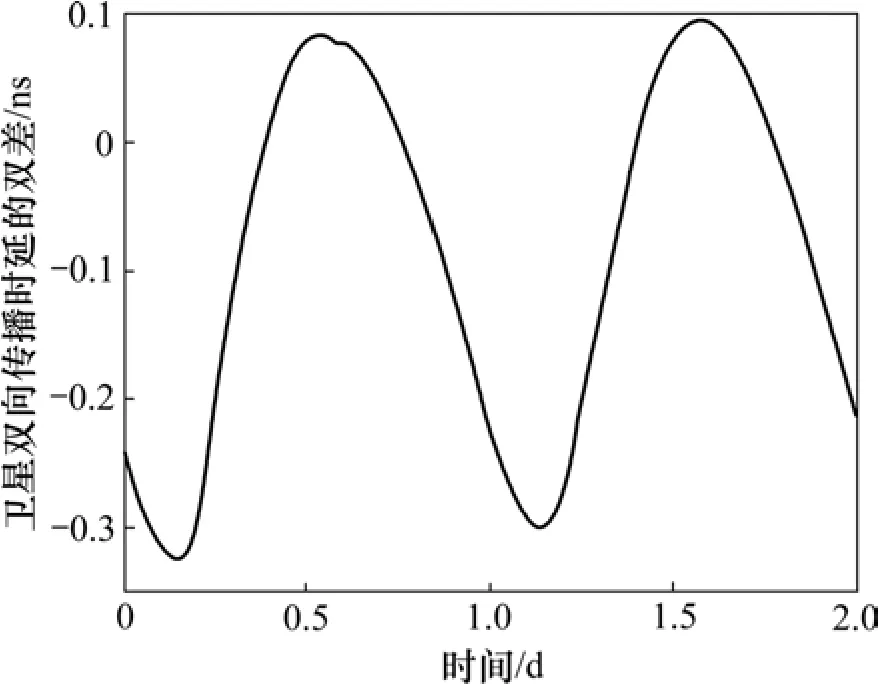
图7 卫星双向传播时延的双差(本文方法与BIPM法计算所得卫星双向传播时延差τUD的差值)Fig. 7 Double difference of two-way propagation delay (the difference of non-reciprocity of satellite two-way propagation delay τUD calculated by method introduced in this work and BIPM method)

4 结论

(1) 提出了一种估计信号传播路径，结合卫星星历和迭代法精确计算卫星双向时间频率传递(TWSTFT)中双向传播时延差的新方法。该方法的特点在于：通过修正卫星位置或者地面站位置来进行Sagnac效应修正，并由此获得信号真实传播路径，并以此为基础，综合考虑地面站到卫星的几何距离时延、Sagnac效应、电离层时延修正、对流层时延修正，计算双向空间传播时延差。该方法只依赖于卫星星历、两地面站坐标和接收信号时刻，可推广应用于采用IGSO卫星等非静地轨道卫星的TWSTFT中。另外，还可继续研究两地面站时间与卫星星历的参考时间之差造成的影响。

(2) 本文方法能够精确估计卫星双向传播时延差，反映卫星运动对TWSTFT的影响；并发现卫星运动不但引起双向几何距离时延差(包含 Sagnac效应修正)幅度达0.412 ns的日波动和均值达77 ps的偏差，对于实验中的C波段TWSTFT链路而言，还造成了双向电离层时延差幅度达0.120 ns的日波动和均值达31 ps的偏差，必须从双向测量结果中扣除，否则将在钟差中叠加具有偏差的日波动，影响对站间钟差的评估。

[1]Bauch A, Piester D, Fujieda M, et al. Directive for operational use and data handling two-way satellite time and frequency transfer (TWSTFT)[R]. Paris: BIPM, 2011: 6−8.

[2]周善石. 基于区域监测网的卫星导航系统精密定轨方法研究[D]. 上海: 中国科学院研究生院, 2011: 31−36.ZHOU Shanshi. Studies on precise orbit determination theory and application for satellite navigation system with regional tracking network[D]. Shanghai: Graduate University of Chinese Academy of Sciences, 2011: 31−36.

[3]Hongwei S, Imae M, Gotoh T. Impact of satellite motion on two-way satellite time and frequency transfer[J]. Electronics Letters, 2003, 39(5): 482−483.

[4]Piester D, Bauch A, Fujieda M, et al. Studies on instabilities in long-baseline two-way satellite time and frequency transfer(TWSTFT) including a troposphere delay model[C]// The 39th Annual Precise Time and Time Interval Systems and Applications Meeting. Long Beach, 2007: 211−222.

[5]武文俊, 李志刚, 杨旭海, 等. 卫星双向时间频率传递中的Sagnac效应[J]. 宇航学报, 2012, 33(7): 936−941.WU Wenjun, LI Zhigang, YANG Xuhai, et al. Sagnac effect on two-way satellite time and frequency transfer[J]. Journal of Astronautics, 2012, 33(7): 936−941.

[6]Tseng W H, Feng K M, Lin S Y, et al. Sagnac effect and diurnal correction on two-way satellite time transfer[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(7):2298−2303.

[7]Parker T E, Zhang V. Sources of instabilities in two-way satellite time transfer[C]// Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition. Vancouver, 2005:745−751.

[8]杨旭海, 李志刚, 李伟超, 等. 基于小倾角 IGSO卫星的双向时间传递试验[C]// 2007全国时间频率学术会议论文集. 宜昌,2007: 372−376.YANG Xuhai, LI Zhigang, LI Weichao, et al. Two-way time transfer experiment based on small obliquity IGSO satellite[C]//2007 National Time and Frequency Research Conference Proceeding. Yichang, 2007: 372−376.

[9]HAN Chunhao, YANG Yuanxi, CAI Zhiwu. Beidou navigation satellite system and its time scales[J]. Metrologia, 2011, 48(4):s213−s218.

[10]黄勇, 胡小工, 王小亚, 等. 中高轨卫星广播星历精度分析[J].天文学进展, 2006, 24(1): 81−87.HUANG Yong, HU Xiaogong, WANG Xiaoya, et al. Precision analysis of broadcast ephemeris for medium and high orbit satellites[J]. Progress in Astronomy, 2006, 24(1): 81−87.

[11]李星, 耿淑敏，李垣陵. 双向时间同步系统的设备时延校准技术研究[J]. 中国空间科学技术, 2011, 31(4): 23−28.LI Xing, GENG Shumin, LI Yuanling. Equipment delay calibration technique for two-way time synchronization system[J]. Chinese Space Science and Technology, 2011, 31(4):23−28.

[12]Kaplan E D, Hegerty C J. GPS原理与应用[M]. 2版. 寇艳红,译. 北京: 电子工业出版社, 2008: 229.Kaplan E D, Hegerty C J. Understanding GPS principles and applications[M]. 2nd ed. KOU Yanhong, trans. Beijing:Publishing House of Electronics Industry, 2008: 229.

[13]Kouba J. A guide to using International GNSS service (IGS)products[EB/OL]. [2009−05−13]. http://igscb.jpl.nasa.gov/igscb/resource/pubs/UsingIGSProductsVer21.pdf

[14]Farrell J, Barth M. The global positioning system and inertial navigation[M]. New York: McGraw Hill, 1998: 156.

[15]叶其孝, 沈永欢. 实用数学手册[M]. 北京: 科学出版社, 2010:740.YE Qixiao, SHEN Yonghuan. Hand book of applied mathematics[M]. Beijing: Science Press, 2010: 740.