岩质边坡爆破振动速度高程效应

蒋楠，周传波，平雯，徐星，路世伟

(中国地质大学(武汉) 工程学院，湖北 武汉，430074)

在露天矿山开采、大型水电开挖等岩质高边坡工程中，爆破开挖技术得到了广泛应用。爆破作业过程引起的震动效应会影响到边坡岩体结构稳定性。为保证高边坡稳定安全，明晰高程影响下边坡爆破振动传播机理，控制爆破震动效应是工程应用中关键科学技术问题。边坡爆破振动高程影响研究国内外开展较多，多以现场测试或实验数据分析为主[1−5]。郭学彬等[3]根据不同爆破振动测试实例，分析了不同类型的坡面对爆破振动的高程放大效应。谭文辉等[4]通过现场实测来探寻高差变化对K和α影响的基本规律，研究边坡高程对爆破效应的影响。刘美山等[5]结合小湾水电站岩石高边坡爆破振动实测数据，采用考虑高程效应的萨氏公式分析爆破振动边坡传播规律。近年来，数值模拟技术也应用到高程效应研究当中，并取得了一定的成果[6−10]。陈明等[9]采用有限元数值模拟研究岩质边坡开挖爆破高程放大效应。Havenith等[10]对Anaaevo岩滑堆斜坡进行有限元数值分析，发现振动波的放大和应变局部化有很大关系。本文作者通过分析影响边坡爆破振动速度相关物理量，基于量纲分析理论推导并改进表征高程影响的爆破振动速度计算模型，结合大冶铁矿东露天采场工程实际，对不同坡度边坡爆破振动数值模拟，分析高程对爆破振动速度衰减的影响，为控制边坡爆破震动效应以及进一步研究爆破振动高程效应机理提供依据。

1 反映高程影响的爆破振动速度经验公式改进

爆破地震波在高边坡岩体内传播衰减受到爆源、边坡体介质条件(如岩性、节理和地质构造等)、爆源距及高程差因素影响。在岩体介质中传播所涉及的主要变量归纳结果，如表1所示[11]。

由量纲分析白金汉定理(π定理)，边坡岩体质点峰值振动速度(v)可表示为：

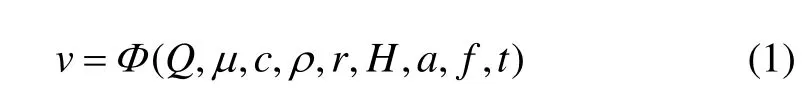
根据π定理，其中独立量纲取为Q，r和c，以π代表无量纲量，则有：

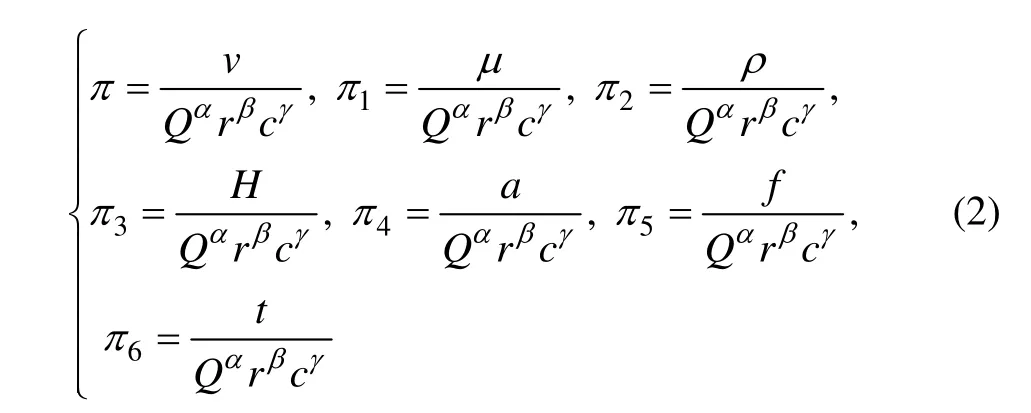
表1 边坡爆破振动涉及到的重要物理量Table 1 Important physical quantities involved in blasting vibration of slope

式中：α，β和γ为待定系数。根据量纲齐次定理，则有：

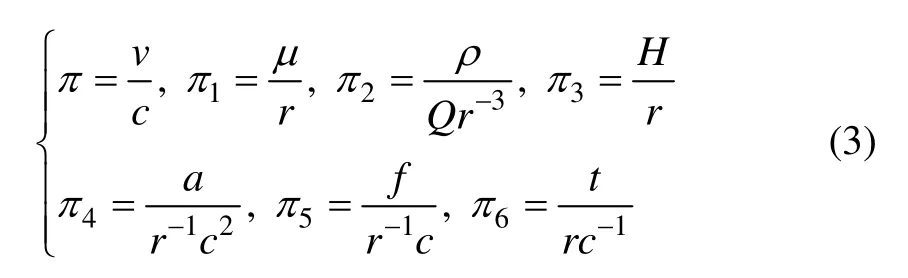
将式(3)代入式(1)可得：

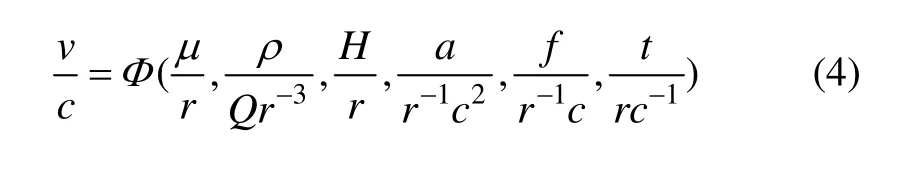
由于不同无量纲数π的乘积和乘方仍为无量纲数，取π2和π3进行如下组合，得到新的无量纲数π7：

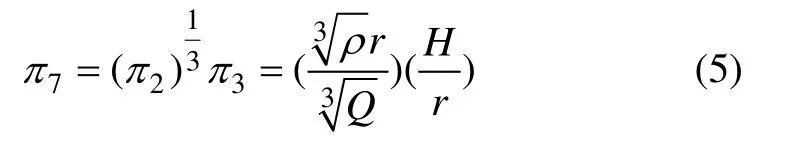
对于某一场地，ρ和c可以近似为常数。因而，由式(5)可以认为具有函数关系。考虑振动速度与H/r的衰减关系。

同时，为分析H/r所表征意义，引入边坡坡度的概念，即H/r为测点与爆源之间相对坡度i的大小，H/r～i存在对应关系。综上所述，可将这函数关系写成：

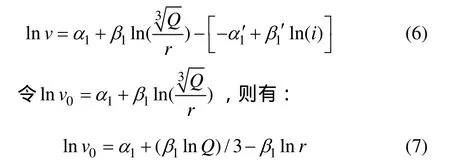
式中：−β1lnr表示爆破振动速度随距离r的衰减；β1为衰减指数主要反映场地介质条件的影响；而α1+(β1lnQ)/3则综合反映了坡体介质条件与炸药量对边坡岩体质点振动的贡献。

令 lnk1=lnα1，则有：

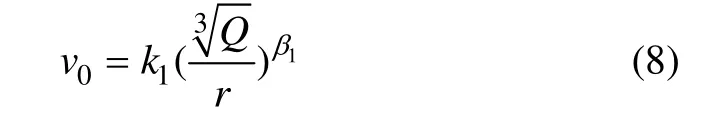
式(8)是不存在高程差影响下平整地形条件的萨道夫斯基公式[12]。将式(8)代入式(6)可得到：

令：lnk2=lnα1′，β2＝−β1′，则式(9)可变为：

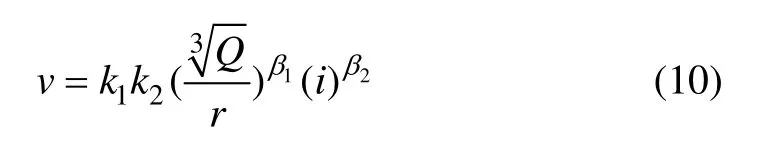
令k=k1k2，则有：

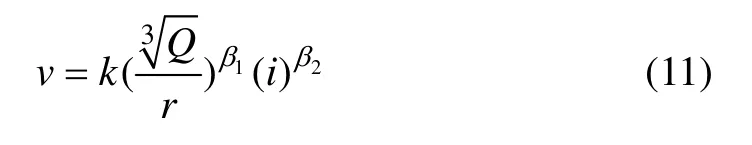
式中：k为场地影响系数；β1为衰减系数；β2为边坡坡度影响效应系数。

对比式(8)和式(11)可知：爆破振动速度在边坡坡面岩体内衰减过程受到测点与爆源之间相对坡度的影响，而此相对坡度与高边坡坡度存在密切的关系。

2 边坡爆破数值计算及验证

ANSYS/LS-DYNA动力有限元软件因其在爆炸力学计算中的优越性，被广泛应用于模拟边坡爆破动力响应研究中[6−8]。采用数值模拟软件，建立爆破振动边坡响应计算模型，模拟分析爆破振动作用下不同坡度岩质边坡坡面岩体振动响应机制，揭示边坡爆破振动高程效应特征。

2.1 模型与参数

采用LS-DYNA数值模拟软件，建立以大冶铁矿东露天采场狮子山北帮边坡工程为背景的边坡模型，根据现场工程地质条件，狮子山北帮边坡以闪长岩为主，边坡高度最高达到432 m，边坡角为43°～46°。对边坡数值计算模型进行简化，建立边坡数值模型坡高100 m，边坡角拟定45°。

模拟过程中，炮孔布置参考北帮边坡挂帮矿开采爆破参数(2011—11—02挂帮矿开采)，拟定炮孔直径80 mm，孔深12 m，孔数5个，炮孔间距4 m，炮孔与坡角间距为5 m，采用多孔同段孔底起爆。由于模型具有对称性，为减少计算量，取模型的1/2进行网格划分及计算分析。模型顶面为自由面，正面(包含半孔的面)作为对称面，其他 4个面均采用无反射边界(non-reflecting boundary)的边界条件，如图1所示[13]。

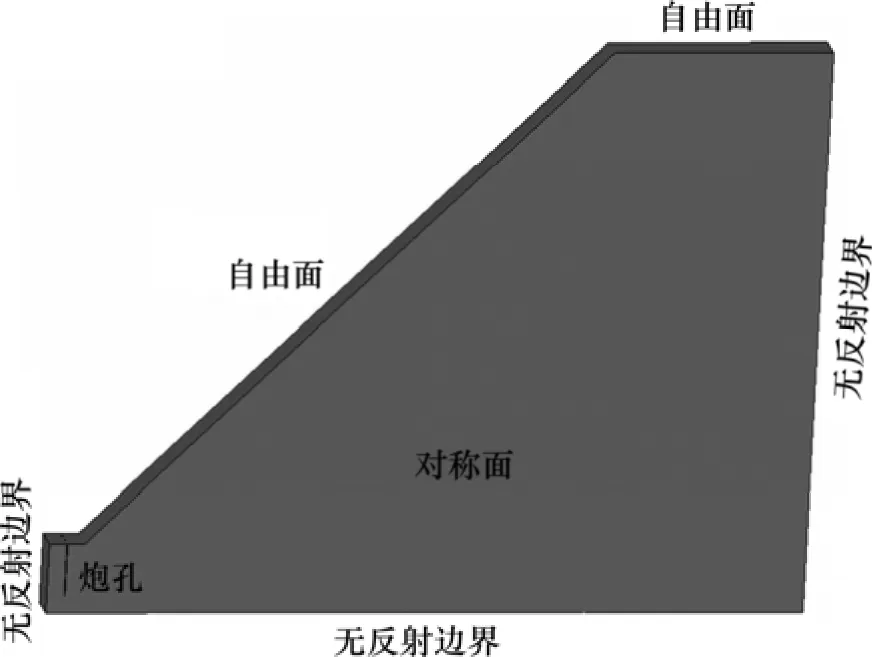
图1 45°边坡数值计算模型Fig. 1 Numerical calculation model of 45° slope

结合现场试验与室内实验，采场狮子山北帮边坡闪长岩物理力学参数，如表2所示。

表2 闪长岩物理力学参数Table 2 Physical and mechanical parameters of diorite

模拟炸药爆轰过程中压力和比容的关系为 JWL状态方程[14]：

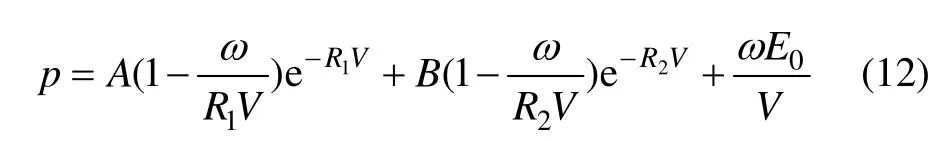
式中：A，B，R1，R2和ω为材料常数；p为压力；V为相对体积；E0为初始比内能。模拟炸药采用跟现场试验一致的二号岩石炸药，起爆单段药量为219 kg，参数见表3。

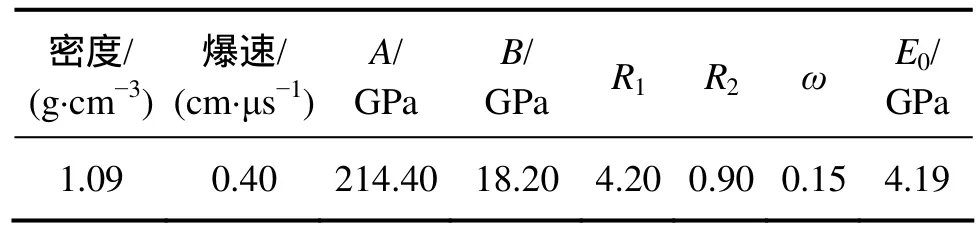
表3 炸药材料物理力学参数Table 3 Material parameters of explosive

2.2 计算分析与验证

爆炸应力波在边坡体内传播，受高程变化的影响，边坡岩体产生爆破振动响应。为分析爆破振动速度沿边坡面变化规律及高程效应，在边坡沿坡面选取一系列监测点进行统计分析，如图2所示。

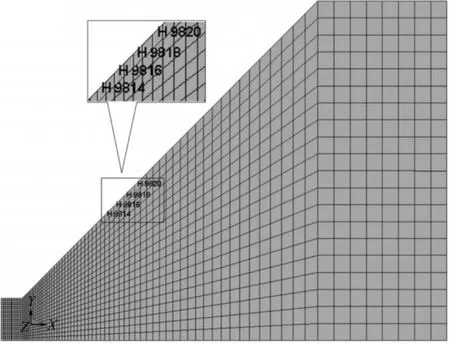
图2 45°边坡选取监测点布置图Fig. 2 Positions of monitoring points in 45° slope

监测点H 9814，H 9816，H 9818和H 9820，沿坡面向上依次选取，与爆源之间的水平距离、高程差依次增加。对所选取监测点垂直、水平方向振动速度进行监测，其中水平方向振动速度时程曲线如图3所示。

由图3可知：监测点H 9814处水平方向最大振动速度为1.103 cm/s，监测点H 9816处水平方向最大振动速度为0.801 cm/s，监测点H 9818及H 9820处水平方向最大振动速度分别为0.565 cm/s和0.429 cm/s。计算结果表明：随着与爆源之间的水平距离、高程差的增加，监测点水平方向振动速度依次递减。爆破振动速度沿坡面衰减明显，且振动峰值出现时间的依次顺延表明爆炸应力波沿坡面传播的时间过程。垂直方向振动速度变化特征相同。

为了验证数值模拟计算结果是否合理，结合现场挂帮矿开采实际，在狮子山北帮边坡对挂帮矿开采进行爆破振动测试。现场监测点沿边坡面布置，与数值计算监测点位置一致。现场测试选用TC−4850型爆破振动记录仪系统。爆破振动数值计算及现场监测数据见表4。其中H 9818现场监测水平方向振动速度时程曲线如图4所示。

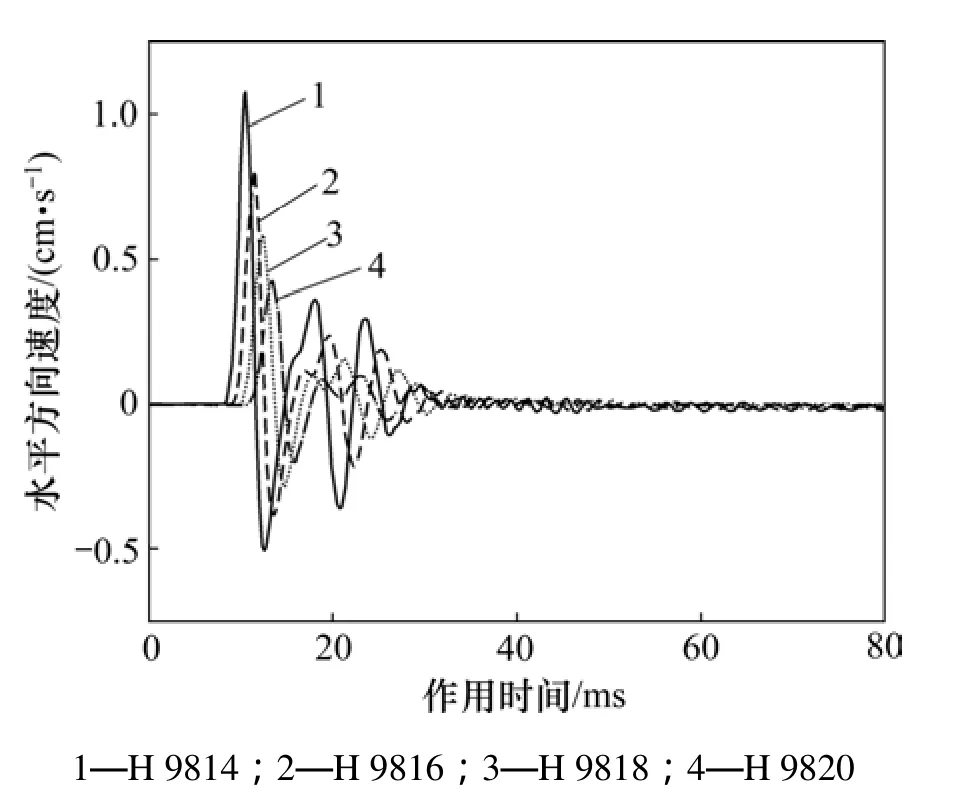
图3 45°边坡选取监测点水平振动速度时程曲线Fig. 3 Horizontal velocity of monitoring points in 45° slope

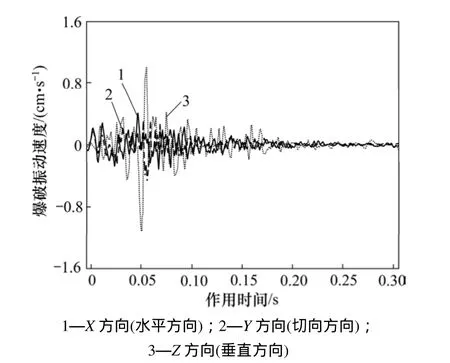
图4 H 9818现场监测水平方向振动速度时程曲线Fig. 4 Field monitoring horizontal vibration velocity of point H 9818

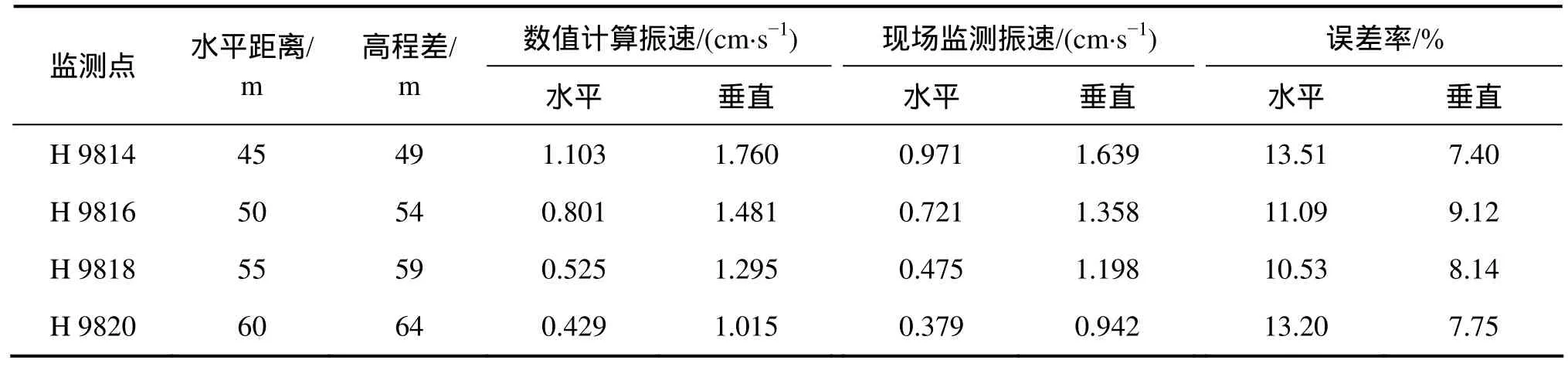
表4 45°边坡监测点爆破振动数值计算及现场监测数据Table 4 Numerical simulation and field monitored PPVs at monitoring points in 45° slope

由表4和图4可知：现场监测数据略小于数值计算结果，但两者数据基本一致；监测点数值计算及现场监测振动速度时程曲线变化趋势基本相同。分析各数据误差率，两者数据相差在可接受范围之内。分析现场监测数据略小的原因在于数值模拟过程未考虑岩体内可能存在固有裂隙对爆破振动速度衰减的影响[15]。研究结果表明：数值计算模型及参数选取合理，数值计算能够较好地反映爆炸应力波在岩质高边坡岩体内的传播规律。

3 边坡爆破振动速度高程效应分析

为分析边坡坡度及高程对爆破振动速度的影响机制，采用已得到验证的计算模型及参数，分别再依次建立不同坡度(坡角依次为 15°，30°和60°)边坡爆破三维数值模型进行计算分析。

3.1 同一边坡坡体内爆破振动速度高程效应

为分析同一边坡体内爆破振动速度高程效应，在边坡模型中，同一水平、不同高程处选取一系列监测点进行监测。以15°(坡度26.8%)边坡为例，如图5所示。

在离爆源水平距离60 m处，由上至下依次选取监测点H 8314，H 8254，H 8194和H 8134进行爆破振动速度监测，不同高程各监测点爆破振动数据见表5。

图5 15°边坡选取监测点布置图Fig. 5 Positions of monitoring points in 15° slope

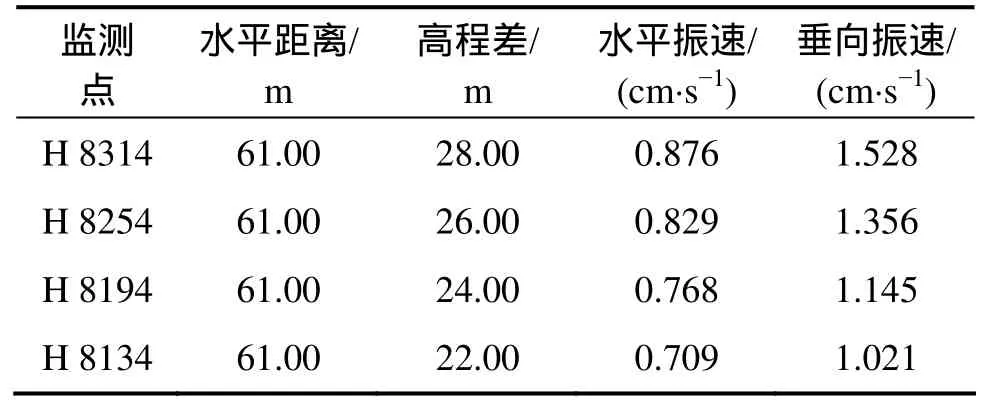
表5 15°边坡不同高程监测点爆破振动数值计算数据Table 5 Numerical simulation PPVs at monitoring points at different altitudes in 15° slope

由表5可知：边坡体内同一水平距离处，监测点爆心距虽在增加，但振动速度却随着高程增加而加大，靠近坡面监测点振动速度越大，且水平振速与垂向振动随高程的放大程度存在不一致，表明：高程对边坡爆破振动响应的影响存在，水平方向振动速度随高程变化响应不够明显，边坡振动速度的放大效应主要以垂直方向振动速度放大为主。

3.2 同一边坡坡面爆破振动速度高程效应

爆炸应力波在边坡体内传播，受高程变化的影响，边坡岩体产生爆破振动响应。为分析爆破振动沿边坡面响应特点及变化规律，在不同坡度边坡沿坡面选取一系列监测点进行统计分析。以30°(坡度57.7%)边坡为例，如图6所示。

图6 30°边坡选取监测点布置图Fig. 6 Positions of monitoring points in 30° slope

监测点H 7346，H 7349，H 7352和H 7355，沿坡面向上依次选取，与爆源之间的水平距离、高程差依次增加。由表6可知：随着与爆源之间的水平距离、高程差的增加，各监测点水平、垂向振动速度依次递减，爆破振动速度沿坡面衰减明显。

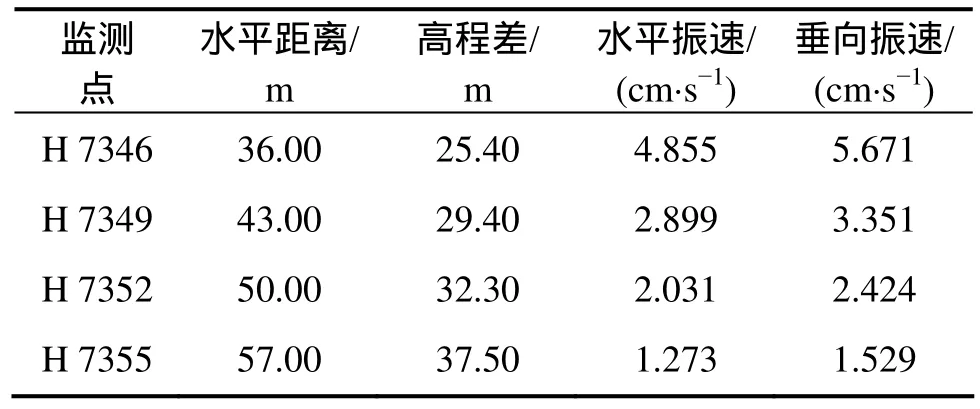
表6 30°边坡不同高程监测点爆破振动数值计算数据Table 6 Numerical simulation PPVs at monitoring points at different altitudes in 30° slope

3.3 不同边坡同一水平处坡面爆破振动速度高程效应

对不同坡度边坡进行爆破动力数值计算，同时在与爆源之间水平距离相同处选择多组坡面监测点进行分析，得到各监测点的垂向爆破振动速度数据，如表7所示。

由表7可知：对于在同一边坡坡面的监测点随着水平距离、高程差的增大，爆破振动速度均呈不断衰减的趋势，随着高程增大的放大效应并没有明显体现。

对于不同坡度边坡，在同一水平处各坡面监测点爆破振动速度变化趋势如图7所示。由图7可知：当测点距离爆源水平距离25 m处时，边坡坡角由15°变化至 30°，随着测点高程的增大，爆破振动速度也随之增大，高程放大效应明显；而其他水平处测点，随着高程的增大，爆破振动速度的衰减趋势明显，放大效应并不占主导。

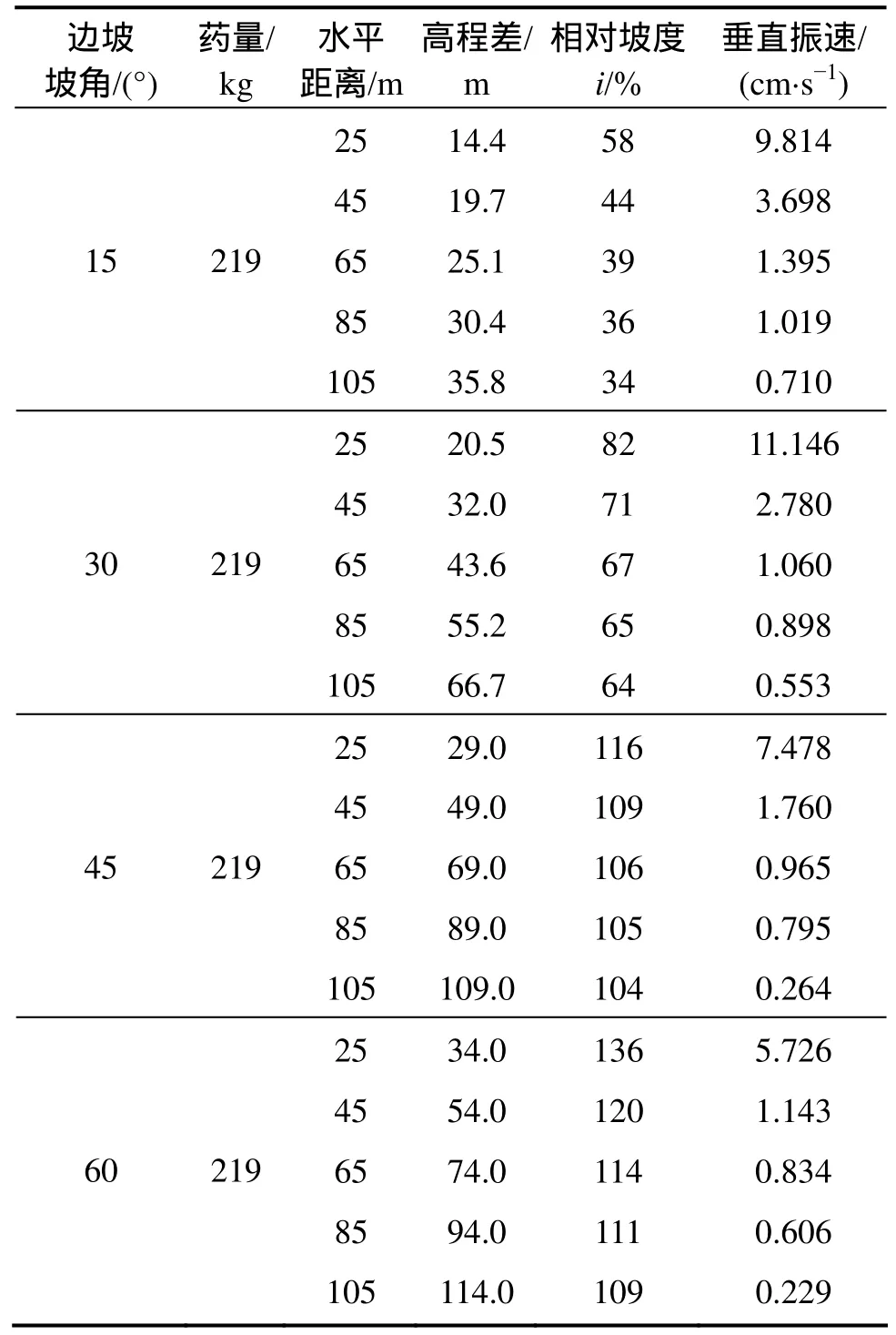
表7 各边坡监测点爆破振动数值计算数据Table 7 Numerical simulation PPVs at monitoring points in slopes

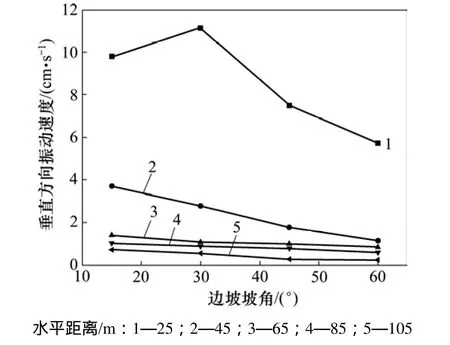
图7 各坡面监测点爆破振动速度变化趋势图Fig. 7 Change trend of PPVs at monitoring points on slope surfaces

3.4 爆破振动速度经验公式预测分析

采用式(8)(萨氏公式)和式(11)分别对表 7中所列监测数据进行回归拟合，得到表征爆破振动传播规律的经验公式，如表8所示。同时依据拟合曲线相关性系数评价2种经验公式对爆破振动速度的预测精度。

由表8可知：随着边坡坡度的增加，采用考虑高程影响的式(11)及不考虑高程影响的萨氏公式(8)进行预测爆破振动速度的相关性系数均在变小，表明预测精度均在降低，说明随着边坡坡度的增加，爆破振动在坡面的传播规律更加的复杂，经验公式对爆破振动速度传播规律的表征有限。对比式(11)和式(8)拟合结果，采用考虑高程影响改进后的式(11)拟合曲线相关性系数更高，表明采用式(11)对爆破振动速度预测精度更高，能更好地反映爆破振动在边坡面的传播规律。

分析表8中所列式(11)和式(8)拟合曲线的相关性系数，对于15°边坡上监测数据，式(11)拟合曲线的相关性系数较比式(8)的提高了0.023；而对于60°边坡上监测数据，式(11)拟合曲线的相关性系数较比式(8)则提高了0.061。以上分析表明：随着边坡坡度的增加，相比式(8)和式(11)对爆破振动速度预测精度提高逐渐明显，采用式(11)预测爆破振动速度能够对边坡高程的影响进行更好地修正。

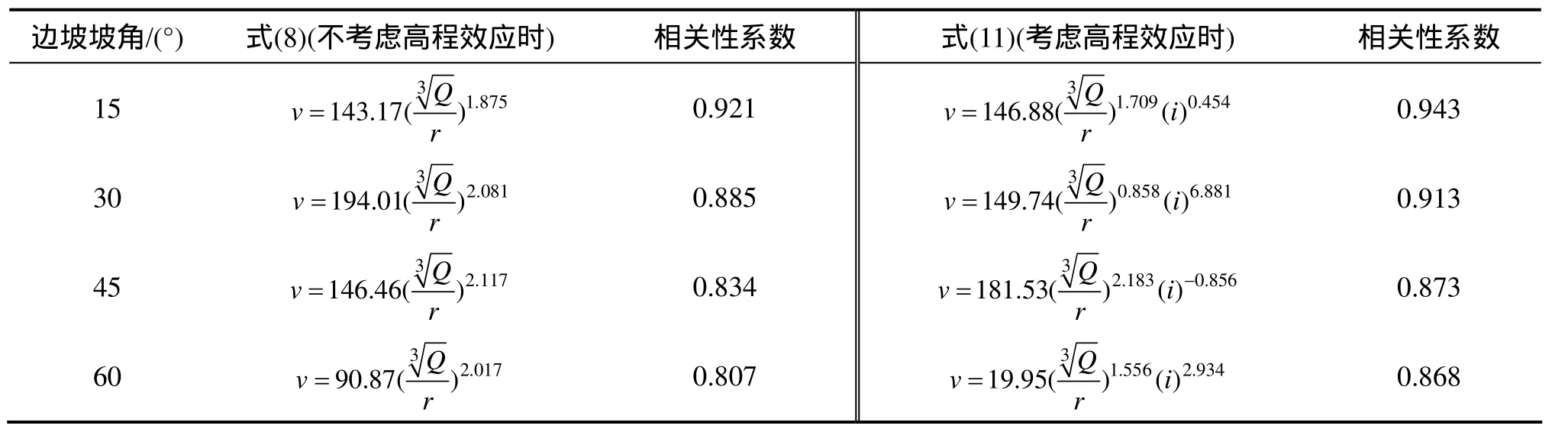
表8 各边坡监测点爆破振动回归分析Table 8 Regression analysis of at monitoring points in slopes

4 结论

(1) 基于量纲分析理论，推导分析得到考虑边坡爆破振动测点与爆源之间相对坡度影响的爆破振动速度衰减规律经验公式。

(2) 采用LSDYNA数值模拟软件，分别建立不同坡度(坡角依次为 15°，30°，45°和 60°)边坡爆破数值模型并进行计算分析，结果表明：对于同一边坡坡体内同一水平距离监测点，高程对边坡爆破振动速度的影响存在，水平方向振动速度随高程变化响应不够明显，边坡振动速度的放大效应主要以垂直方向振动速度放大为主；对于同一边坡坡面监测点，随着与爆源之间的水平距离、高程差的增加，各监测点水平、垂向振动速度依次递减，爆破振动速度沿坡面衰减明显；对于不同坡度边坡，在同一水平处各坡面监测点爆破振动速度随着边坡坡度的增加同样以衰减为主，但当测点距离爆源水平距离25 m处时，边坡坡角由15°变化至 30°，随着测点高程的增大，爆破振动速度也随之增大，高程放大效应较比衰减趋势占主导。

(3) 对不同坡度(坡角依次为 15°，30°，45°和 60°)边坡爆破数值计算结果回归分析表明：随着边坡坡度的增加，相比式(8)，式(11)对爆破振动速度预测精度提高逐渐明显，采用式(11)预测爆破振动速度能够对边坡高程的影响进行更好地修正。

[1]唐海, 李海波. 反映高程放大效应的爆破振动公式研究[J].岩土力学, 2011, 32(3): 820−824.TANG Hai, LI Haibo. Study of blasting vibration formula of reflecting amplification effect on elevation[J]. Rock and Soil Mechanics, 2011, 32(3): 820−824.

[2]Marrara F, Suhadolc P. Site amplifications in the city of Benevento(Italy) comparison of observed and estimated ground motion from explosive sources[J]. Journal of Seismology, 1998,2(2): 125−143.

[3]郭学彬, 肖正学, 张志呈. 爆破振动作用的坡面效应[J]. 岩土力学与工程学报, 2001, 20(1): 83−87.GUO Xuebin, XIAO Zhengxue, ZHANG Zhicheng. Slope effect of blasting vibration[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(1): 83−87.

[4]谭文辉, 璩世杰, 毛市龙, 等. 边坡爆破振动高程效应分析[J].岩土工程学报, 2010, 32(4): 619−623.TAN Wenhui, QU Shijie, MAO Shilong, et al. Altitude effect of blasting vibration in slopes[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(4): 619−624.

[5]刘美山, 吴从清, 张正宇. 小湾水电站高边坡爆破震动安全判据试验研究[J]. 长江科学院院报, 2007, 24(1): 40−43.LIU Meishan, WU Congqing, ZHANG Zhengyu.Experimentation on judging standard of blasting vibration safety in high slope excavation of Xiaowan hydropower station[J].Journal of Yangtze River Scientific Research Institute, 2007,24(1): 40−43.

[6]许名标, 彭德红. 某水电站边坡开挖爆破震动动力响应有限元分析[J]. 岩土工程学报, 2006, 28(6): 770−775.XU Mingbiao, PENG Dehong. Finite element analysis of dynamic response on blasting vibration in slope excavation of a hydroelectric power station[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 770−775.

[7]SONG Xiaolin, ZHANG Jichun, GUO Xuebin, et al. Influence of blasting on the properties of weak intercalation of a layered rock slope[J]. International Journal of Minerals, Metallurgy and Materials, 2009, 16(1): 7−11.

[8]何理, 钟冬望, 陈江伟. 爆破载荷作用下混凝土边坡动力响应数值分析[J]. 武汉科技大学学报, 2011, 34(2): 123−125.HE Li, ZHONG Dongwang, CHEN Jiangwei. Numerical analysis of dynamic response of concrete slope under blasting load[J]. Journal of Wuhan University of Science and Technology,2011, 34(2): 123−125.

[9]陈明, 卢文波, 李鹏, 等. 岩质边坡爆破振动速度的高程放大效应研究[J]. 岩石力学与工程学报, 2011, 30(11): 2189−2195.CHEN Ming, LU Wenbo, LI Peng, et al. Elevation amplification effect of blasting vibration velocity in rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11):2189−2195.

[10]Havenith H B, Vanini M, Jongmans D. Initiation of earthquakeinduced slope failure: influence of topographical and other site specific amplification effects[J]. Journal of Seismology, 2003,7(3): 397−412.

[11]唐海. 地形地貌对爆破振动波影响的实验与理论研究[D]. 武汉: 中国科学院岩土力学研究所, 2007.TANG Hai. Field experimental and theoretical study on blasting wave propagation characteristics under different terrains[D].Wuhan: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, 2007.

[12]GB 6722—2011, 爆破安全规程[S].GB 6722—2011, Safety Regulations for Blasting [S].

[13]Chen M, Lu W B, Yi C P. Blasting vibration criterion for a rock-anchored beam in an underground powerhouse[J].Tunneling and Underground Space Technology, 2007, 22:69−79.

[14]LSTC. LS-DYNA keyword user’s manual[M]. Livermore,California: Livermore Software Technology Corporation, 2003:128−129.

[15]Jiang N, Zhou C B. Blasting vibration safety criterion of a tunnel liner structure[J]. Tunneling and Underground Space Technology,2012, 32: 52−57.