拉锥球透镜光纤和柱状楔形透镜光纤与半导体激光器耦合的比较研究
卢胜强,郑煜,邓圭玲,段吉安
(中南大学 高性能复杂制造国家重点实验室,湖南 长沙,410083)
影响半导体激光器(laser diode,LD)与单模光纤(single-mode fiber,SMF)耦合效率的主要因素可分为内部原因与外部原因2种。SMF中的基模场在光纤截面内具有特定的分布,对于阶跃型光纤,此分布为零阶贝赛尔函数,可近似为高斯函数[1],SMF 的模场可以近似为高斯场。然而,LD的模场分布总是呈现出非圆对称,并常常偏离高斯场型,因此LD与SMF两者在模场分布上不匹配,这会在很大程度上影响耦合的效率。除此之外,内部原因还包括了菲涅耳反射等因素[2]。外部原因即位置不对准,包括纵向间隙误差、横向偏移与角度偏差等引起的耦合效率的损耗[3]。目前LD与SMF的耦合方式很多,概括起来可分为分离式透镜耦合和光纤微透镜耦合两种。由于光纤微透镜耦合效率较分离式透镜耦合有了很大程度上的提高,有些耦合方式可以达到 70%甚至 80%以上[4−6],现在已经开始逐步替代分离式透镜耦合。光纤微透镜耦合的方式多种多样,不同方式之间的耦合效果差别是巨大的。但不管采用何种耦合技术,都应该考虑到耦合效率与对准容忍度的平衡,在追求更高的耦合效率的同时,也要考虑到对准和封装过程的可实现性。本文作者建立了拉锥球透镜光纤(spherical lensed fiber,SLF)[7]和柱状楔形透镜光纤(cylindrical lensed fiber,CLF)[8]2种微透镜与LD耦合的模型,研究了SMF通过这2种方式与LD耦合时的耦合效率、位置不对准对耦合效率的影响以及容忍度等问题,并对这2种耦合方式进行了多方面的比较。
1 理论模型
图1所示为LD与SMF耦合的各参数的示意图,其中,平面1为激光的出射面,d为横向偏移,Ф为角度偏差,z为激光出射面到透镜光纤端面的纵向距离,r为透镜在该方向上的半径。定义如图1所示的dx与Фx分别为x方向上的横向偏移与角度偏差,依此把x替换为y则dy与Фy分别为y方向上的横向偏移与角度偏差。
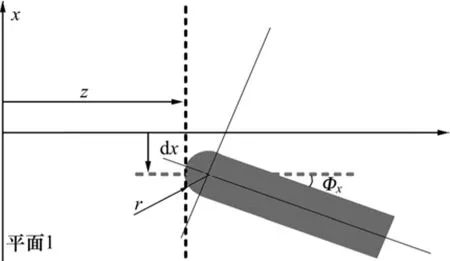
图1 耦合系统参数示意图Fig. 1 Schematic diagram of parameters in coupling system
本文对(InGa)(AsP)/InP双异质结激光器进行分析,该激光器有关参量如下:有源层厚度2 μm,有源层宽度 6 μm,有源层折射率n1=3.42,衬底折射率n2=3.21,x为垂直于结平面方向,光束发散角为θ⊥=38.27°,y为平行于结平面方向,光束发散角θ∥=13.00°[9],光束的束腰半径由式(1)和式(2)分别计算得ωox=1.202 μm,ωoy=3.660 μm。另外,激光器的出射波长为1 310 nm,SMF的模场半径取典型值ωof=4.65 μm[10]。

菲涅耳反射对耦合效率的影响可以通过在透镜光纤的端面涂一层抗反射膜来消除[11],因此,LD与SMF耦合的实质就是它们模场之间的耦合。LD的场分布总是偏离高斯场型,为不规则的场分布,但在理论模型中,通常将LD模场近似为高斯分布[12]。拉锥球透镜光纤、柱状楔形透镜光纤与LD耦合的模型分别如图2(a)与2(b)所示。

图2 透镜光纤与LD的耦合模型Fig. 2 Coupling models of lensed fiber to LD
在LD与SMF的耦合中,耦合效率可通过式(3)得到。通过计算,可以得到耦合效率与纵向间距、透镜半径、横向偏移、角度偏差之间的关系。

式中:ψ1与ψ2分别为LD和SMF在某一参考面上的模场分布[13]。
2 2种耦合方式的比较
2.1 最佳耦合效率的比较
通过 Mathematica软件仿真,获得不存在横向偏移与角度偏差的情形下SLF和CLF这2种耦合方式的耦合效率与纵向间距z、透镜半径r的关系,如图3(a)和3(b)所示。由此得到各自的最大耦合效率值以及在获得最大耦合效率时相对应的纵向间距z与微透镜半径r。

图3 耦合效率与z和r的关系Fig. 3 Coupling efficiency as a function of z and r
SLF最大耦合效率出现在z=20.87 μm,r=12.26 μm时,最大耦合效率为74.44%。CLF的最大耦合效率出现在z=12.62 μm,r=6.35 μm 时,最大耦合效率为96.09%。可以看出:CLF的最大耦合效率值相比于SLF有着明显的优势,说明单从耦合效率这方面来看,CLF是一种理想的耦合方式。实际上,在本文中,LD的出射光纵横比接近于3:1,如果LD的出射光纵横比较大,比如达到5:1或更大时,使用CLF会有更明显的最大耦合效率上的优势。
为了两者在比较时的方便,取耦合效率损耗为 1 dB处作为容忍度[14],当耦合损耗为1 dB时,CLF的耦合效率为76.33 %,SLF的耦合效率为59.13 %。同时,为了更直观的比较两者,也考察CLF的耦合效率为59.13%(此时CLF的耦合损耗为2.11 dB)时允许的误差。
2.2 透镜加工精度的比较
在对准耦合过程中,纵向间距z为可调整的因素,而透镜半径r在加工时就已经成型,不易改变。从图3可以看到:SLF的容忍区域比CLF的容忍区域大。考虑z分别达到两者的最佳耦合位置时,透镜半径的大小对耦合效率的影响,如图4所示,图4中实线与虚线分别表示耦合损耗为1 dB时CLF与SLF的耦合效率。

图4 耦合效率与透镜半径的关系Fig. 4 Coupling efficiency as a function of radius
在损耗1 dB时,拉锥球透镜光纤的前端球半径容许在7.96~29.03 μm范围内,而柱状楔形透镜光纤前端的圆柱半径容许范围较小,仅为4.33~10.35 μm,允许波动的范围不到前者的 1/3,即使是在同样达到59.13%的耦合效率时,其容许范围为3.62~19.50 μm,仍然小于SLF允许的加工误差。可见:在对透镜光纤端面进行加工时,SLF的精度要求较CLF的要宽松。考虑到目前微透镜制造工艺的加工精度,制作理想的CLF是完全可以达到的[15−16]。
2.3 纵向、横向偏移对耦合效率的影响
透镜半径取各自最大耦合效率处的值,假设不存在角度偏差,对纵向间距误差、横向偏移与耦合效率的关系进行分析,其在x,y和z方向上位置偏移对耦合效率的影响如图5所示。
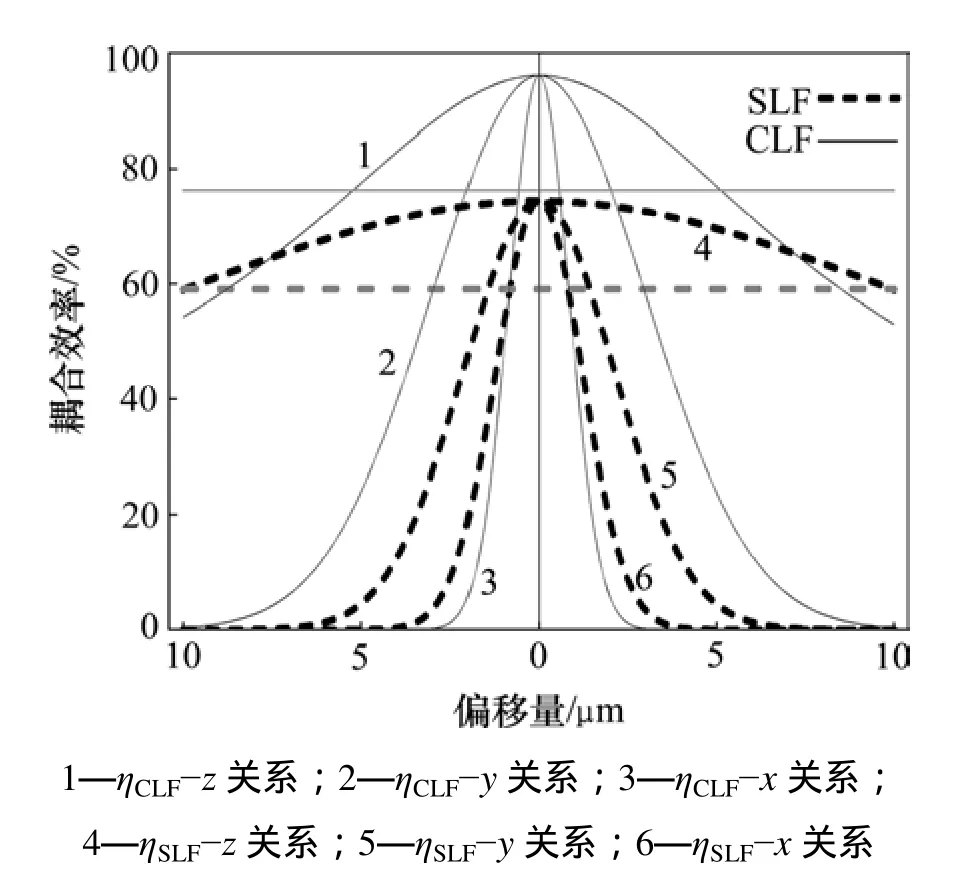
图5 耦合效率受各向偏移的影响Fig. 5 Coupling efficiency as functions of offset
在各自的透镜半径都达到理想状况下,对2种透镜而言,在x,y和z3个方向上,容忍度从大到小依次为z,y,x。并且可以看出:z方向上的容忍度较其他2个方向明显宽松,这一点两者是一致的;对两者的各向容忍度分别进行比较,拉锥球透镜的z与x2个方向上的容忍度都比楔形柱状透镜的大,而在y方向上楔形柱状透镜有更大的容忍度。2种透镜耦合方式在各个方向上的位置偏移容忍度如表1所示。

表1 x,y和z方向上的位置偏移容忍度Table 1 Offset tolerance of x, y and z
从表1和图5可见:CLF的x方向的容忍度最小,为 0.57 μm,对对准及封装的精度要求最高,而这也决定了对平台的精度要求。当CLF损耗为2.11 dB时,它在x和y方向上的允许误差范围较SLF的容忍度大。z方向上虽然较SLF的容忍度要小,但与x和y方向相比明显更加宽松,其意义不大。由此表明在仅有纵向、横向偏移的条件下,虽然CLF在容忍度上较严格,但当以耦合效率同样达到 59.13%为参考标准时,CLF的要求比SLF宽松。
2.4 角度偏差对耦合效率的影响
对于SLF,由于其结构是轴对称的,透镜光纤绕z轴旋转而产生的角度偏差Фz并不会影响耦合效率。而对于CLF,由于柱状楔形透镜的特殊结构,Фz也会对耦合效率造成影响,但其容忍度与x和y方向相比要大的多,因此不对它做过多研究。
与上面一样,透镜的半径取各自最大耦合效率处的值,假设不存在横向偏移与纵向间距误差,对角度偏差Фx和Фy与耦合效率的关系进行分析。角度偏差在x和y方向上对耦合效率的影响如图6所示。

图6 耦合效率受角度偏差的影响Fig. 6 Coupling efficiency as a function of tilt
2种透镜在角度偏差对耦合效率的影响上呈现出的差别较小,无论是SLF还是CLF,其在y方向上的角度偏差容忍度都较x方向大。角度偏差的容忍度如表2所示。
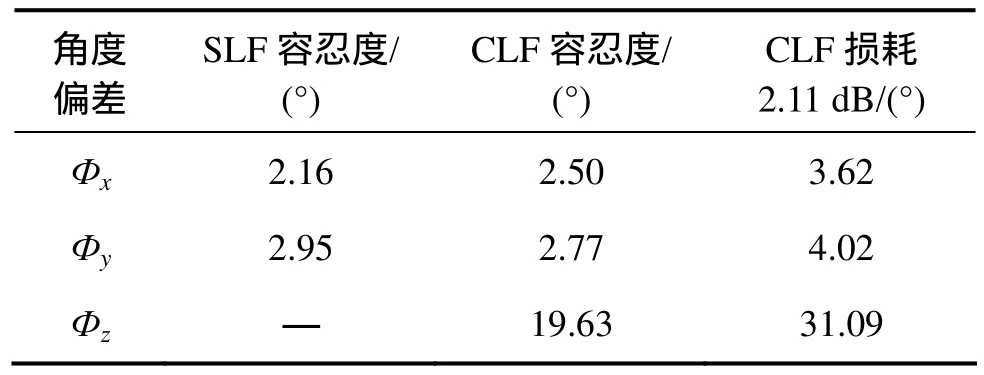
表2 x,y和z方向上的角度偏差容忍度Table 2 Tilt tolerance of x, y and z
SLF在x方向的角度偏差容忍度是最小的,CLF在x方向与y方向的角度偏差容忍度相近。虽然在y方向上CLF容忍度要略小于SLF容忍度,但从总体上看,CLF的角度偏差容忍度较SLF的理想。在CLF在损耗为2.11 dB时,其允许的误差就明显比SLF要大。从表2可以看出:在仅存在角度偏差的条件下,CLF无论从耦合效率还是从容忍度上,都比 SLF要理想。
2.5 横向偏移与角度偏差同时存在时
当横向偏移和角度偏差同时存在时,除了横向偏移与角度偏差各自会产生耦合损耗外,还会有一个附加的耦合损耗[17],因此不能把横向偏移和角度偏差做简单的叠加。
SLF与 LD耦合时,在取得的最大耦合效率74.44%处,x和y方向的耦合效率相等,都为86.28%。假设在单个方向上损失1 dB,而另一个方向上没有损耗,则2个方向上耦合效率分别为68.53%与86.28%。如果假设在x和y2个方向上各损失0.5 dB,则2个方向上的耦合效率均为76.90%。因此,对于SLF,把耦合效率68.53%与76.90%作为重要的参考点。
同样的,CLF与 LD耦合时,在取得最大耦合效率96.09%处,x方向的耦合效率为99.97%,已经接近耦合极限,在损失1 dB时其耦合效率为79.43%,损失0.5 dB时耦合效率为89.12%;在最大耦合效率值处y方向的耦合效率为96.12%,损失1 dB时耦合效率为85.67%,损失0.5 dB时耦合效率为76.35%。
图7(a)和7(b)所示分别为SLF与LD耦合过程中横向偏移与角度偏差同时存在情况下x方向上和y方向上的耦合效率;图7(c)和7(d)所示分别为CLF与LD耦合过程中横向偏移与角度偏差同时存在情况下x方向上和y方向上的耦合效率。
在x方向上对SLF与CLF两者进行比较,当同样达到1 dB损耗时,两者允许的容忍区域大小接近,在横向偏移上相比,SLF比CLF允许的最大偏移量略大,但在角度偏差上,通过调动横向偏移,CLF允许有比SLF更大的角度偏差。同样的,在y方向上对两者进行比较,SLF与CLF的容忍区域相差不多,CLF显得更加规整。两者允许的最大横向偏移很接近;而在角度偏差上,SLF比 CLF允许有更大的角度偏差。对0.5 dB点进行分析时,可以得出相似的结论。从总体上看,当同时存在有横向偏移与角度偏差时,两种耦合技术在容忍范围上并未呈现出太大的差距。

图7 横向偏移与角度偏差同时存在时对耦合效率的影响Fig. 7 Coupling efficiency when both offset and tilt are present
综合考虑横向偏移、纵向偏移、角度偏差对耦合效率的影响,无论是SLF还是CLF,在x方向的容忍度都是最严格的,其中,x方向上的横向偏移对精度要求非常高,而相对于横向偏移,角度偏差容忍度是比较大的,比较容易控制。因此,在对准与封装过程中,横向偏移是优先于角度偏差的因素。在容忍度上,考虑到在相同耦合效率时所允许的对准误差,相较于CLF,SLF并未显示出显著的优势。
3 结论
(1) 在使用上面提到的LD与SMF进行耦合时,CLF的耦合效率有极大的优势,最大值可达96.09%,是一种理想的耦合方式。
(2) 在对微透镜的加工上,SLF所需的精度较CLF的要低,在制作上比较容易实现,但制造理想的CLF也是完全可以实现的。
(3)x方向的横向偏移容忍度要求是最严格的,而角度偏差相对容易控制,横向偏移应是优先于角度偏差考虑的因素。
(4) 考虑到耦合效率与对准容忍度的平衡,在与LD的耦合中,CLF有更好的表现,使用CLF比SLF更有优势。
[1]刘德明, 孙军强, 鲁平, 等. 光纤光学[M]. 北京: 科学出版社,2008: 101.LIU Deming, SUN Junqiang, LU Ping, et al. Optical fiber of the light[M]. Beijing: Science Press, 2008: 101.
[2]HE Yongzhi, Mondal S K, Shi F G. Design optimization of wedge-shaped lensed fibers for fiber-laser coupling: Fresnel reflection and non-Gaussian mode effects[J]. Lightwave Technology, 2003, 21(10): 2271−2273.
[3]淳静, 吴宇列, 李圣怡. 半导体激光器与单模光纤自动对准[J]. 光电工程, 2005, 32(8): 32−35.CHUN Jing, WU Yulie, LI Shengyi. Automatic alignment between a laser diode and a single-mode fiber[J].Opto-Electronic Engineering, 2005, 32(8): 32−35.
[4]Yeh S M, Huang S Y, Cheng W H. A new scheme of conical-wedge-shaped fiber endface for coupling between high-power laser diode and single-mode fibers[J]. Lightwave Technology, 2005, 23(4): 1781−1786.
[5]Yang H M, Chen C T, Ro R Y, et al. Investigation of the efficient coupling between a highly elliptical Gaussian profile output from a laser diode and a single mode fiber using a hyperbolic-shaped microlens[J]. Optic & Laser Technology, 2010, 42(6): 918−926.
[6]Hidehiko Y, Kazuo S. A new scheme of a lensed fiber employing a wedge-shaped graded-index fiber tip for the coupling between high-power laser diodes and single-mode fibers[J]. Lightwave Technology, 2001, 19(12): 1910−1917.
[7]MA Yan, XIE Fuzeng. Design of a tapered lens for semiconductor laser to single-mode fiber coupling[J]. Chinese Journal of Semiconductors, 2004, 25(11): 1355−1359.
[8]ZHANG Quan, TANG Haiqing. Angular alignment tolerances for a 980nm pump laser diode coupled to a cylindrical lensed fiber[J]. Acta Photonica Sinica, 2003, 32(1): 92−96.
[9]LU Wenlong, ZHENG Yu, ZHAO Wenlong, et al. Analysis coupling between a laser and a single-mode fiber with a ball lens based on Monte Carlo method[J]. Laser Technology, 2012, 36(3):338−341.
[10]淳静. 光纤有源器件激光焊接封装的关键技术研究[D]. 长沙:国防科学技术大学机电工程与自动化学院, 2006: 38.CHUN Jing. Study on the key techniques of fiber active devices packaging with laser welding[D]. Changsha: National University of Defense Technology. College of Mechatronic Engineering and Automation, 2006: 38.
[11]Poxson D J, Schubert M F, Mont F W, et al. Broadband omnidirectional antireflection coatings optimized by genetic algorithm[J]. Optics Letters, 2009, 34(6): 728−730.
[12]吕百达. 激光光学: 光束描述、传输变换与光腔技术物理[M].北京: 高等教育出版社, 2003: 1−7.LÜ Baida. Laser optics: Beam characterization, propagation and transformation, resonator technology and physics[M]. Beijing:Higher Education Press, 2003: 1−7.
[13]Ammon Y, Pochi Y. 光子学—现代通信光电子学[M]. 陈鹤鸣,施伟华, 汪静丽, 译. 北京: 电子工业出版社, 2009: 183−184.Ammon Y, Pochi Y. Photonics: Optical electronics in modern communications[M]. CHEN Heming, SHI Weihua, WANG Jingli, transl. Beijing: Publishing House of Electronics Industry,2009: 183−184.
[14]Toyoshima M. Maximum fiber coupling efficiency and optimum beam size in the presence of random angular jitter for free-space laser systems and their applications[J]. Journal of Optical Society of America A, 2006, 23(9): 2246−2250.
[15]WANG Zhiyou, LÜ Yushan. The study of optical fiber micro-lens’s manufacture method[J]. Development & Innovation of Machinery & Electrical Product, 2007, 20(4): 28−30.
[16]Pollciove H, Gloini D, Ruckman J. Computer [aided]optics manufacturing[J]. Optics and Photonics News, 1994, 5(6):15−19.
[17]Massimo L, Fabio E Z. Optical coupling from plane wave to step-index single-mode fiber[J]. Optic Communications, 2004,237(1/2/3): 37−43.

