推土机智能造型控制系统研究

赵庆松，李东艳

（潍坊工程职业学院 山工机电工程学院，山东 青州 262500）

0 引言

在高尔夫球场造型时，球场平面、斜面造型要求越来越新颖且复杂多变，这就需要操作者具有非常高的操作技能。研究推土机造型控制系统是为了适应特定的造型需要，如斜坡造型、平整等。操作带有本系统的推土机，操作者无需较高的操作技能，只需要输入特定的指令，如造型斜坡15°，在斜坡起始点打开造型使能开关，推土机会按指令要求自动的根据车速快慢调节铲刀升降速度，用倾角传感器的反馈数据作为铲刀动作的结束条件，完成特定的造型任务。

1 系统组成

推土机智能造型控制系统可以分解为电气控制系统和液压控制系统。电气控制系统的组成如图1 所示，包括：可编程控制器、电控比例阀、铲刀控制输入单元、行走控制输入单元和速度传感器等。液压控制系统如图2 所示，包括：液压泵组、电控比例阀和液压缸等。

图1 电气控制系统

图2 液压控制系统

2 系统控制的原理

控制器根据推土机车身的倾角传感器和车体速度传感器上传数据，计算出铲刀上升、下降所需调整量，以电流的形式发给铲刀升降电控比例阀，控制液压油的流向及流量，从而自动控制铲刀的动作快慢，铲刀倾角传感器用作检测铲刀位姿角度，约束铲刀动作始终，满足推土机不同角度造型的需要。同时车身倾角传感器检测车体与水平面的角度，用作车体防倾翻保护。

3 系统控制流程

智能造型控制系统控制流程如图3 所示。控制器如果收到控制单元上传的数据，分配各电控比例阀电流，控制液压系统使推土机行走和铲刀动作。如果收到造型角度指令和使能数据时，控制器根据速度传感器数据和造型角度数据计算出电磁阀电流，分配给被控电磁阀，铲刀自动动作，在铲刀中没有土料时，驾驶员返回，再次运土，完成下一次工作循环。

图3 系统控制流程

4 智能造型控制系统的实现

智能造型系统是在行走系统和铲刀工作系统基础上实现的。控制器采集车身位姿角度，与驾驶员输入的造型角度通过一系列的公式计算，计算出铲刀理论提升或者下降的角度，再根据几何关系和液压系统参数关系，计算出满足理论提升或者下降的角度所需要的流体体积，根据测速传感器测得的速度及车体参数计算车完成上升、下降动作各自需要的时间，计算车液压系统的流量大小，再由电液系统的参数关系，计算控制需要输出的控制电流，从而驱动电液比例阀利用液压油完成铲刀的提升和下降，满足斜面造型的需要，同时采集铲刀倾角传感器角度变化，参考铲刀理论提升或者下降的角度确定铲刀的位置，完成造型的需要，整个过程不考虑铲刀重力作用。下面以推土机从平面开始斜面造型建立数据模型进行分析研究，当推土机不在水平面开始造型时，可以根据车身倾角传感器测得角度数据对铲刀提升、下降的角度进行补偿，满足造型目标斜面的要求，实现自动造型。

5 数学模型的建立

1）推土机铲刀升降模型的建立。

推土机斜面造型模型建立如图4 所示。推土机在水平面上进行土料搬运，当铲刀到达斜面起点B 时，铲刀开始提升。推土机继续向前运动，铲刀继续提升，当履带前端到达起点B，铲刀提升终止，铲刀开始下降。

如图5 所示，当履带后端到起点E 时，铲刀下降结束。在任意时刻，如果铲刀没有土料，驾驶员控制推土机后退重新搬运土料重复进行以上动作。

根据图4 所示，当造型斜面角度为α，履带前端点和斜面起始点重合，铲刀提升角度为δ 时，可得：

图4 斜面造型铲刀提升终点模型

图5 斜面造型铲刀下降终点模型

式中：LOA为铲刀动作铰接点到履带底平面的距离；LOB为铲刀动作铰接点到履带底面前端的距离。

式中：LOD为铲刀动作铰接点到铲刀底面的距离；LOB为铲刀动作铰接点到履带底面前端的距离。

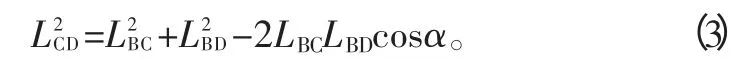
式中：LBC为履带底面和铲刀底面处于同一平面时履带前端到铲刀的距离；LCD为造型时铲刀动作的距离。

式中：LOC为履带底面前端到铲刀底面的距离。

根据图5 所示可以确定铲刀下降角度与提升角度相等。

2）斜面造型控制模型的建立。

根据图6 所示，得：

式中：η 为推土机推平时的铲刀对应角度；LMN为推土机推平时升降液压缸长度。

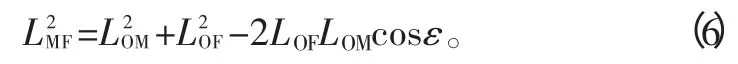
式中：LMP为履带前端点和斜面起始点重合时液压缸长度；ε为履带前端点和斜面起始点重合时刻对应的角度。

图6 铲刀动作数学模型图

式中：LMP为如图5 位置时对应的升降液压缸的长度；ΔL 为液压缸缩短的最大长度。

图7 铲刀升降角度与造型角度关系图

式中：SY为升降液压缸有杆腔的横截面积；VS为铲刀提升δ 角度所需要流体的体积。

式中：v 为推土机前进的速度；ts为造型时提升铲刀的时间。

式中：Qs为速度为v、提升铲刀时流量大小。

式中：Sw为升降液压缸无杆腔的横截面积；Vj为铲刀下降δ 角度所需要流体的体积。

式中：LEB为推土机履带长度；tj为铲刀下降时间。

式中：Qj为速度为v、铲刀下降时流量大小。

式中：Q 为流体流量；C 为流量系数；ΔP 为比例阀进出口压力差；A 为比例阀开口横截面积。

式中：k 为截面系数；I为控制器输出电流；m 为门槛值。

假设电磁比例阀开口面积和电流大小成线性对应关系。由式（14）、式（15）可以求得

根据式（1）、式（2）、式（3）、式（4）组成方程组，解出铲刀提升角度

将假设参数LOB=LOA/sinβ=500/sinβ，LOC==（5002+2 0002）0.5，LBC=1 500，β=π/4，带入式（17）中得到δ和α 的关系，如图7 实线所示，定义造型角度最大为π/6。将公式理想化为图中虚线：

假定铲刀底面和履带底面处于同一水平面时，定义液压缸为初始长度，假设以下参数：

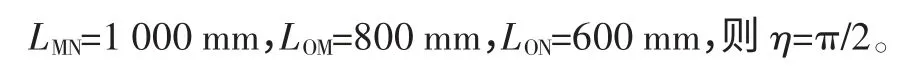
同时根据式（5）、式（6）、式（7）、式（18），得在铲刀提升时，液压缩短的长度与造型斜面角度之间的关系式如下：

根据式（8）、式（9）、式（10）可以得出造型斜面铲刀提升时流量大小与造型角度和车体速度之间的关系并进行单位转换，得如下关系式为：

根据式（14）、式（15）、式（20）可以得出在铲刀提升过程中，控制器输出电流和速度与角度的关系式为：

在负载敏感系统中，ΔP、C、k、m 为常数，ρ 为密度，式（21）可以简化为：

式中a 和b 为常数。

平面造型时，α=0，I=0，得b=0，当以v=3 m/s，造型角最大时，即α=π/6 时需电流最大，比例阀有效宽度假设为0.5 A，可以得出a=177，门槛电流暂定0.1 A，式（22）可以变成：

式中，α=［0，π/6］，v=［0，3］。

根据式（11）、式（12）、式（13）可以得出造型斜面铲刀下降时流量大小与造型角度和车体速度之间的关系并进行单位转换，得关系式为：

根据（14）、式（15）、式（24）可以得出在铲刀下降过程中，控制器输出电流和时间与车体速度和造型角度的关系式：

铲刀下降过程中，对式（25）求解原理与式（21）相同。可以得到：

式中，α＝［0，π/6］，v=［0，3］。

根据式（23）、式（26），在MATLAB 中得到推土机在造型时铲刀提升和下降电流变化规律，如图8、图9 所示。图10、图11 分别为造型角度15°和造型角度30°时电流和速度关系曲线。

图8 提升电流与速度和造型角度关系

图9 下降电流与速度和造型角度关系

6 基于可编程控制器CODESYS程序编写研究

根据式（23）、式（26）电流与角度、速度之间的关系，用CODESYS编程软件编写控制主体功能程序如图12 所示。

图10 造型角度15°电流—速度关系

图11 造型角度30°电流—速度关系

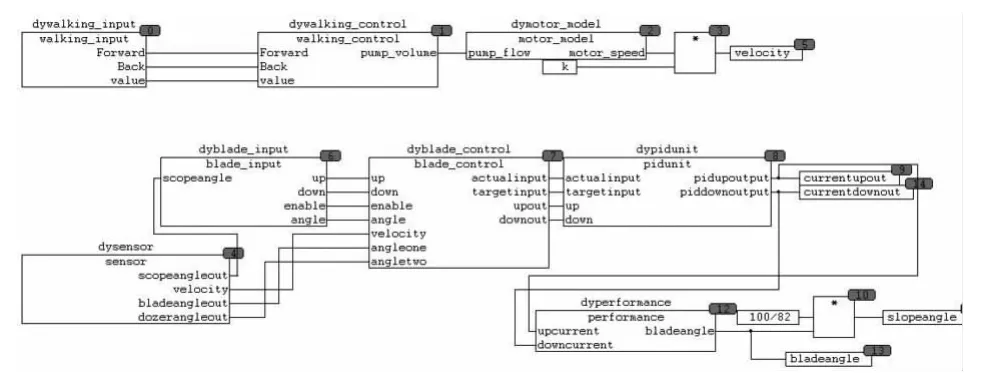
图12 主体程序结构框图

对程序进行研究仿真运行，采用匀加速的速度信号，得到特定造型角度15°、30°时的铲刀升、降电流与速度的关系曲线如图13 所示。

从图13 中可以看出电流与速度的CODESYS 软件仿真输出基本与MATLAB 计算（如图10、11 所示）相符合，仿真数据验证了本系统的实现从理论上完全可行。

图13 造型角度15°和30°时电流—速度关系

7 结语

本文主要设计研究造型推土机智能造型控制系统。通过对推土机功能进行深入研究，并且大胆假设部分参数和简化数据模型，从理论上得出电流与速度和角度的关系。基于CODESYS 编程软件对电流与速度和角度的关系进行仿真研究分析，验证了本系统的实现在理论上是完全可行的。

［1］张新荣，霍莹，王金民.基于PLC 的生产线运料车控制系统设计［J］.制造业自动化，2011（7）：115-118.

［2］吴丽.可编程控制器基础与应用.北京：机械工业出版社，2009.