电机运行状态监控信号工频干扰消除方法

闫新江

(河北中煤四处矿山工程有限公司，河北 邢台 054000)

电机运行状态的监控一般采用对机械旋转过程中振动信号分析的方法来实现，其中振动信号的采集是电机运行状态监控的基础。但是在实际采集到的振动信号中往往包含工频干扰成分，严重影响采集数据的质量和准确性，给振动信号分析带来不便。传统的抑制信号中的工频干扰的方法主要有陷波滤波法和自适应滤波法［1］。但如果有用信号频率成分接近近50 Hz 及其谐波频率时，使用该类方法在抑制工频干扰的同时也会造成有用信号的损失。

基于独立成分分析的盲信号分离技术是根据信号的统计独立性，在混合信号混合信息未知的情况下，从混合信号中分离出相互独立的各个信号分量。随着盲信号分离技术的不断发展，该技术已广泛应用于声音、图像、通信和医学等各领域［2-4］。由于所采集的机械旋转振动信号和工频干扰信号分别产生于不同的信源，信号之间相互独立，可以将工频干扰消除问题转化为盲信号分离问题来解决。

本文采用盲信号分离的方法来实现机械旋转振动信号中工频干扰的消除，提出了一种新的工频干扰消除算法。算法选用信号变化度作为信号分离的目标函数，利用布谷鸟优化方法对目标函数进行优化求解，在对源信号成功分离的情况下实现机械旋转振动信号中的工频干扰消除。由于本算法仅用到了信号的二阶累积量，且每次迭代计算过程中仅重复使用首次迭代前利用混合信号计算出的协方差矩阵，而无须对所有混合信号样本点进行累积量的计算，大大降低了工频干扰消除过程中的计算量。

1 基于信号变化度的盲分离原理

在基于独立分量分析的盲信号分离问题的求解过程中，主要是基于信号独立性的模型。机械旋转过程中的振动信号具有时间上的连续性。因此，可以利用信号中的时间结构信息来实现对源信号的分离。

设来自N 个信号源的信号矢量为s(t)=［s1(t)，s2(t)，…，sN(t)］T，通过瞬时线性混合得到K 个观测信号矢量为x(t)=［x1(t)，s2(t)，…，xK(t)］T，且N=K。混合过程用矢量矩阵表示为:

式中:A 为满秩可逆的混合矩阵。针对逐次盲信号分离过程，分离模型可表示为:

式中:wi为第i 次分离行向量;yi(t)为第i 次分离出的某一路源信号的估计，即

式中:i=1，2，…，N;k=1，2，…，N;λk为加权系数。

根据文献［6］，信号变化度的定义为:

式中:j'=1，2，…，N。由信号变化度的定义可知

最大化Vyi(wi)所得到的分离信号yi即为源信号sk的估计［5］。因此，盲信号分离问题的目标函数即为:

本文利用布谷鸟优化算法求解使目标函数J(wi)达到最大值的分离向量wi，即可得到信号变化度最大的一路源信号的估计。

2 布谷鸟算法

布谷鸟优化算法［6，7］是近几年继蚁群算法、粒子群算法和人工蜂群等仿生群智能优化方法之后新提出的一种仿生智能优化算法，算法模拟布谷鸟选巢产卵的行为对函数进行优化求解，该算法具有参数少、容易实现、寻优能力强等优点。下面对布谷鸟优化算法的求解原理进行简要介绍。

布谷鸟算法是模拟布谷鸟繁殖后代的策略提出的一种优化算法，布谷鸟自己不会孵化下一代，通常把卵下到其它鸟的鸟巢中，卵如果被其它鸟发现，该卵会被丢弃。算法遵循以下三条规则:

规则1:一只布谷鸟一次只产一个蛋，随机选择一个鸟巢存放;

规则2:蛋最好的鸟巢被保存，生成下一代;

规则3:可用鸟巢数量固定，卵被发现的概率是Pa∈［0，1］。

算法假设可用鸟巢的个为N，每一个卵代表空间向量的一个解，随机初始化解X=(X1，X2，…，XNe)，计算每个解的适应度值f(Xi)。

首先根据Levy flight 随机游动，即式(7)对初始值进行更新

式中:a 是步长因子，决定随机搜索范围，Levy(λ)服从Levy概率分布，见式(8)。

比较f(Xi)和f(Xnew)，如果f(Xnew)优于f(Xi)，则Xnew替换Xi。

当卵被发现时，该卵所对应的解被抛弃，并根据式(9)生成新的解:

式中:r 是缩放因子，是［0，1］区间的随机数。

3 基于布谷鸟优化的工频干扰消除算法

3.1 算法原理

采集到的含有工频干扰的微弱信号可表示为:

式中:s(t)为有用信号，r(t)为工频干扰信号，参数A、f0、θ0分别为工频干扰的幅度、频率和相位。为加权系数。由于在实际机械振动信号等微弱信号的采集过程中，通常只能得到单路观测信号。因此，可以通过人工构造观测信号的方法将工频干扰消除问题转化为盲信号分离问题。本文采用文献［9］的方法构造观测信号，由于

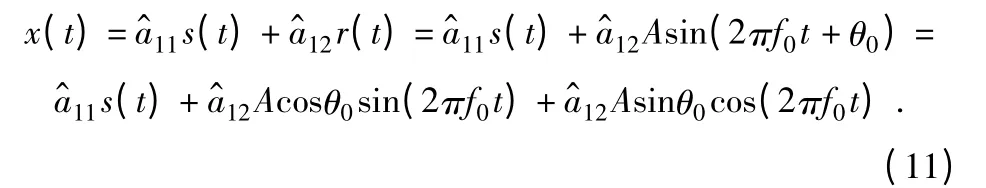
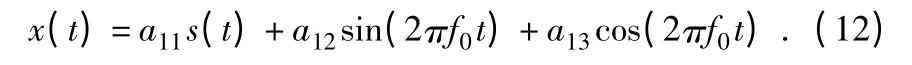
可见观测信号中除了有用信号s(t)外，还含有a12sin(2πf0t)和a13cos(2πf0t)两路信号成分。因此，可通过额外构造r1(t)=a22(sin2πf0t)和r2(t)=a33cos(2πf0t)两路观测信号，与含有工频干扰的采集信号共同作为待分离的观测信号，即可通过盲分离方法得到抑制工频干扰的有用信号s(t)。

即针对三路信号x(t)、r1(t)、r2(t)执行信号分离过程，本文采用布谷鸟优化算法对式(6)中的目标函数J(wi)进行优化求解，即可得到一路分离信号。进而通过多次分离过程，最终求出已抑制工频干扰的有用信号的估计。

3.2 算法实现步骤

基于信号变化度与布谷鸟优化的工频干扰消除算法的具体实现步骤如下:

步骤1:根据式(12)人工构造两路观测信号r1(t)和r2(t)。

步骤2:对三路观测信号x(t)、r1(t)和r2(t)进行白化和中心化处理。

步骤3:初始化种群，随机产生N 个初始值。

步骤4:根据所有卵当前最优位置由式(2)得到分离信号，计算出每个卵的适应度函数值。

步骤5:对于布谷鸟的每个卵根据式(7)进行更新，如果得到的新卵的适应度函数值优于原卵的适应度函数值，则将原卵替换;否则原卵保持不变。

步骤6:根据概率Pa，选出要丢弃的卵，并根据式(9)产生新的卵。

步骤7:计算每个卵的适应度函数值，记录此时最优解。

步骤8:如果已经达到最大进化代数，则输出当前卵的最优值，根据式(2)得到一路分离信号，针对观测信号执行消源计算过程，进入步骤9;否则返回步骤5。

步骤9:如果已经得到抑制工频干扰的有用信号，退出算法;否则返回步骤3，进行下一次信号分离。

4 仿真分析

算法仿真针对不含工频干扰的振动信号进行分析研究。在一道振动信号中(如图1 所示)加入模拟工频干扰信号)，得到包含50 Hz 工频干扰的振动信号，如图2 所示。

图1 原始振动信号

图2 混有工频干扰的振动信号

根据式(12)构造两路观测信号r1(t)和t2(t)，并与图2中信号共同构成待分离的三路信号。采用本文算法针对待分离信号进行三次信号分离，从而得到不含工频干扰的振动信号。算法中布谷鸟算法的参数设置为:可用鸟巢数量为20，Pa=0.3，进化代数设置为500 代，分离结果如图3 所示。通过比较图1 和图3 可知，本文算法成功实现了对微弱信号采集过程中工频干扰成分的抑制，恢复出了原始振动信号。

图3 本文算法抑制工频干扰输出振动信号波形图

为了更客观地分析本文算法对于工频干扰成分的抑制效果，我们采用重构信噪比对算法进行评价。重构信噪比S/N 定义为［10］:

S/N 的值越大，表示恢复的信号与原始振动信号的误差越小，干扰抑制效果越好。表1 所示为采用本文算法进行20 次仿真恢复出的振动信号与原始振动信号的重构信噪比，每次实验结果的重构信噪比均高于30 dB。可见，本文算法具有良好的工频干扰抑制效果，对原始振动信号具有较高的恢复精度。

表1 恢复信号的重构信噪比

5 结论

在实际机械故障检测中，采集到的机械振动信号中往往包含工频干扰成分，从而影响信号的采集精度。本文在信号变化度理论的基础上，提出了一种布谷鸟优化的工频干扰消除算法。该算法利用人工构造观测信号的方法将工频干扰抑制问题转化为盲信号分离问题，采用人布谷鸟优化算法求解基于信号变化度的目标函数，从而可将不含工频干扰的有用信号成功提取出来。计算机仿真结果表明，本文算法可以很好地抑制采集信号中存在的工频干扰成分，对有用信号的恢复精度较高。

［1］沈凤麟.生物医学随机信号处理［M］.合肥：中国科技大学出版社，1999：441－442.

［2］Mato-Mendez F J，Sobreira-Seoane M A.Blind Separation to Improve Classification of Traffic Noise［J］.Applied Acoustics，2011，72(8) ：590－598.

［3］Ikhlef A，Abed-Meraim K，Guennec D L.Blind Signal Separation and Equalization with Controlled Delay for MIMO Convolutive Systems［J］.Signal Processing，2010，90(9) ：2655－2666.

［4］Ruiz R A S，Ranta R，Louis-Dorr V.EEG Montage Analysis in the Blind Source Separation Framework［J］.Biomedical Signal Processing and Control，2011，6(1) ：77－84.

［5］高鹰，谢胜利.一种线性混合盲提取方法［J］.电子与信息学报，2006，28(6) ：999－1003.

［6］吴炅，周健勇.整数规划的布谷鸟算法［J］.数学理论与应用，2013，33(3) ：99－106.

［7］Yang X S，Deb S.Engineering Optimization by Cuckoo Search［J］.International Joural of Mathematical Modeling and Numerical Optimisation，2010(4) ：330－343.

［8］吴小培，詹长安，周荷琴，等.采用独立分量分析方法消除信号中的工频干扰［J］.中国科技大学学报，2000，30(6) ：671－676.

［9］Bofill P，Zibulevsky M.Underdetermined Blind Source Separation Using Sparse Representations［J］.Signal Processing，2001，81(11) ：2353－2362.