凹梁式半挂车车架的动静态特性分析与计算

侯培海

（1.中航工业安徽开乐专用车辆股份有限公司，安徽阜阳236000；2.宁波大红鹰学院 汽车CAE应用技术研究所，浙江宁波315000）

车架承受着半挂车内外的各种载荷，是影响整车性能的关键部件。虽然车架按等强度设计具有一定的安全系数，但常因轴距较大、路面不平、及载荷不合理等原因，致使车架产生疲劳破坏[1－3]。近年来，由于经典力学方法分析车架的受力情况时，很难得到精确的解析解。一些专家学者开始借助有限元方法对车架强度进行分析研究[1]，企图找出应力分布规律，并对薄弱部位进行改进[4]。但车架结构的复杂性，载荷工况的不确定性，给有限元模拟带来极大的困难，从而限制了有限元方法的应用。

笔者基于已有研究成果，考虑车架的几何特征、悬架系统刚度的非线性变化等因素，建立完整的车架有限元模型，对车架进行满载工况的静态分析；用经典力学方法进行应力分析和计算；最后通过自由模态分析，找出结构的薄弱环节，为结构的改进和动态分析提供一定的理论参考。

1 满载静态分析

1.1 整车设计参数

凹梁式运输半挂车，悬架系统为三桥串联式，满载质量为30000 kg，全车总长为13000 mm，轴距为8800 mm，前悬长350 mm，后悬长240 mm，车架结构图如图1所示。

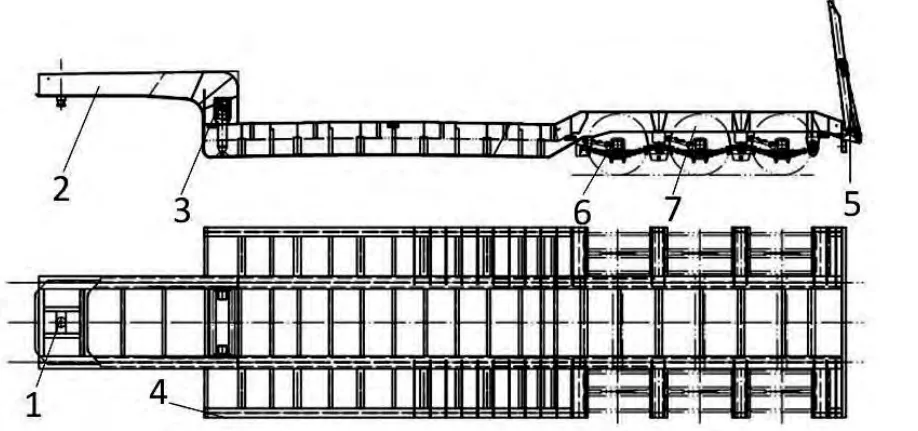
图1 车架结构图

1.2 钢板弹簧有限元模型的建立

基于ABAQUS软件建立悬架系统的有限元模型，其中板簧采用六面体C3D8 单元建模，悬架支架采用四节点shell 单元。由于随着载荷的增加，各片板簧逐渐接触并发生滑移，这是典型的接触行为。为了更好地模拟板簧的这种特性，在片与片之间建立摩擦接触对，采用罚函数接触算法和库伦摩擦模型进行计算，摩擦系数取0.15。图2a为板簧有限元模型图，由于摩擦接触具有强烈非线性属性，需耗费大量资源，为了提高收敛性和计算速度，求解时不允许接触对发生分离，板簧与支架之间采用rigid 刚性连接。

1.3 载荷与边界条件

约束牵引销座处的平移自由度以及x、z方向的旋转自由度，约束悬架系统的全部自由度。满载30t，按照均布载荷的方式施加在凹梁两侧底板上，分析工况为满载静止。车架的有限元模型如图2b所示。

1.4 计算结果与分析

计算得到车架的等效应力及位移云图（图3）。静载工况下，根据文献[4]，该车架最大允许变形为

ymax＝0.003 L＝26.4 mm

从图3b可看出有限元分析得到车架的最大位移为18.7mm，因此，该车架刚度满足设计要求。

计算得到的应力集中区域为鹅颈前端纵梁变截面处、鹅颈处、前平台与凹梁连接处及后平台与凹梁连接处，等效应力值分别为151.6 MPa、191.2 MPa、187.8MPa及124.6Mpa，等效应力云图分别如图4所示。车架采用16Mn 低合金结构钢，屈服极限345 MPa。参考文献[4]取安全系数1.6，则材料许用应力为215.6MPa。由分析结果可知，应力集中区域的最大等效应力小于材料许用应力。因此，满载工况下车架的强度满足设计要求。

图2 板簧及车架有限元模型

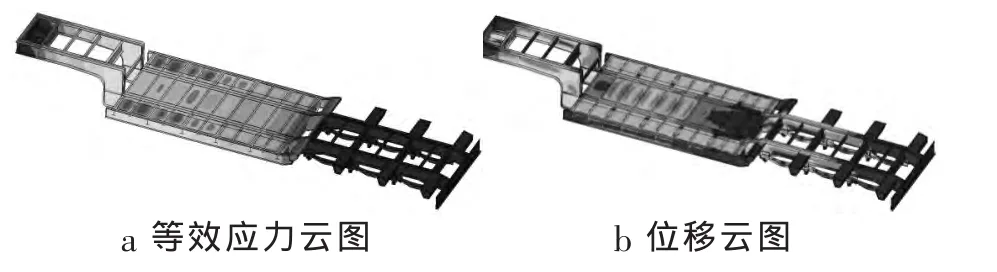
图3 车架的应力及位移云图

图4 应力集中区域的等效力云图

2 经典力学方法的计算与分析

2.1 基本参数与假设

根据车架结构和载荷特点，在计算时引入以下假设和简化：1）载荷以车架纵向中心线对称分布，计算时仅取单个纵梁为研究对象；2）车架纵梁看做前端以牵引座为铰支座，后端以后桥中心为铰支座的简支梁；3）所有作用力均通过纵梁截面的形心且认为是纯弯曲。4）不考虑悬架刚度的影响。

2.2 弯曲应力计算

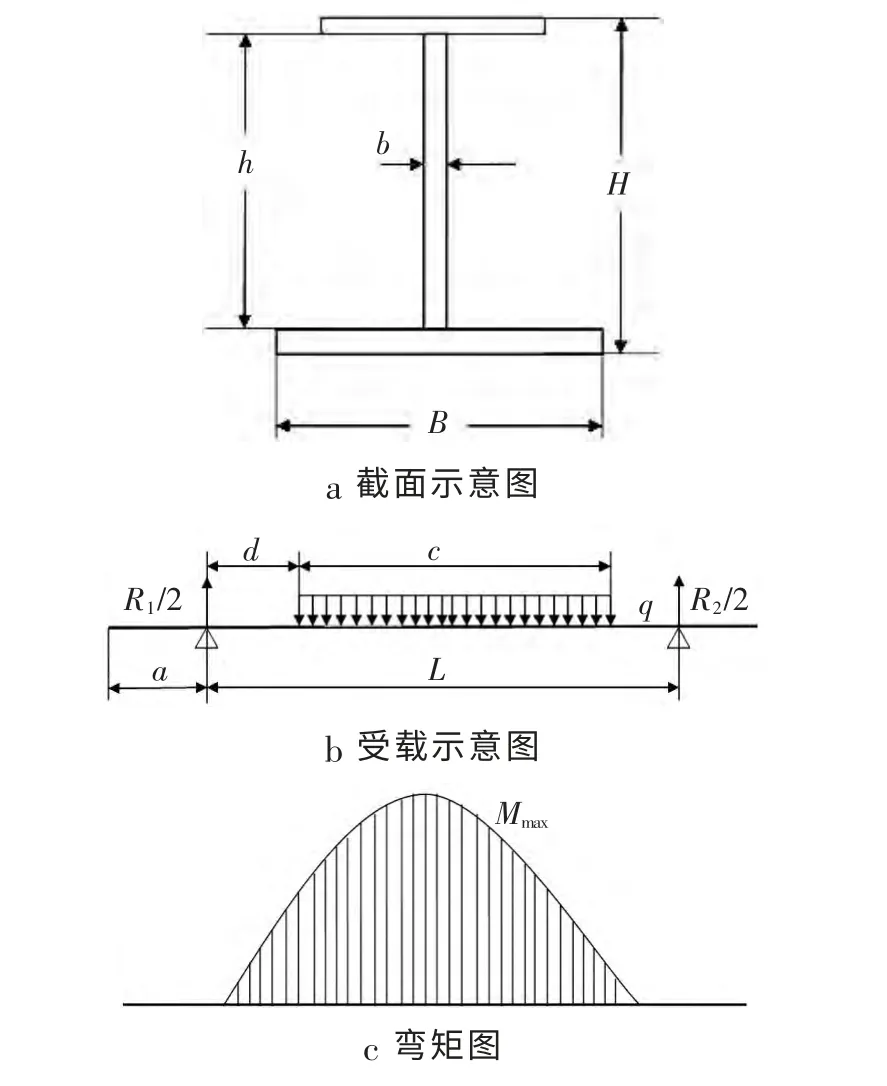
图5 纵梁截面、受载及弯矩图

纵梁采用工字型结构，如图5a所示，图5b为纵梁受载示意图。根据文献[5]，弯矩方程、抗弯截面模量W和应力σ 计算公式分别为

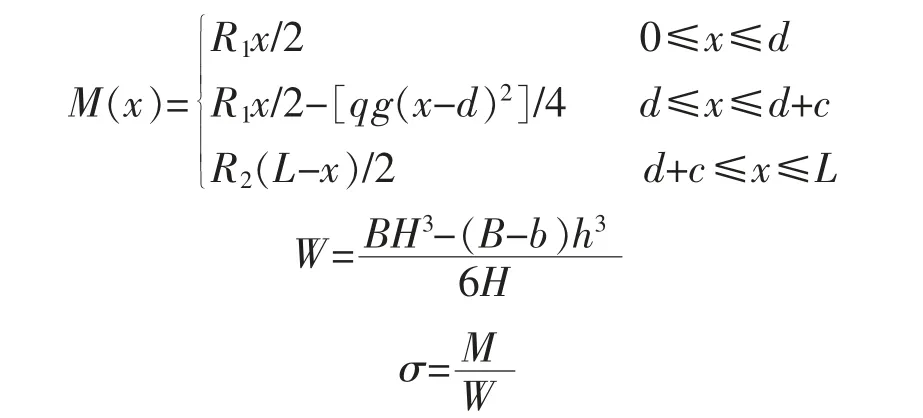
式中：R1为牵引销处支承力，取129868N；R2为后桥支撑力，取166947N；d为牵引销至载荷作用点的距离，取2450mm；c为载荷作用长度，取4660mm；B为翼板宽度；H为工字梁高度；b为腹板厚度；h为腹板高度；M为弯矩。

图5c为纵梁弯矩图，结合纵梁设计参数、弯矩方程及弯矩图，可确定最大弯矩发生在距牵引销5883.1mm处，最大弯矩为270551352.7N·mm，该处截面参数：B为140mm、b为8mm、H为520mm、h为486mm，计算可得抗弯截面模量为1452780.2mm3，因此，最大弯曲应力为186.23MPa。由于车架切应力较小，可将弯曲应力看做等效应力。因此，理论计算的等效应力小于材料的许用应力215.6MPa。有限元分析结果显示该处等效应力为135.4MPa，低于理论计算结果，这是因为理论计算时没有考虑横梁和加强板的影响，导致计算结果偏大。总体来说，有限元分析和理论计算的应力趋势是一致，采用有限元分析方法能够准确地计算车架的应力状态。

3 模态分析

采用Lanzcos 法分析车架的前10阶自由模态。各阶固有频率与振型如表1所示。

车架的1阶和3～5阶振型如图6所示。从计算结果看，车架的振型主要有扭转、弯曲、弯扭组合以及局部振动。1～3阶为扭转振型，频率范围分布在4～12Hz之间；第4阶为弯曲振型；第5阶为二阶扭转振型。6～9阶为局部振动，频率范围为20～28Hz。分析表明：该车架扭转刚度较低，受激共振时易出现局部位置的疲劳损伤，因此，应设法提高扭转刚度并对局部区域的进行加强。

图6 车架的部分振型

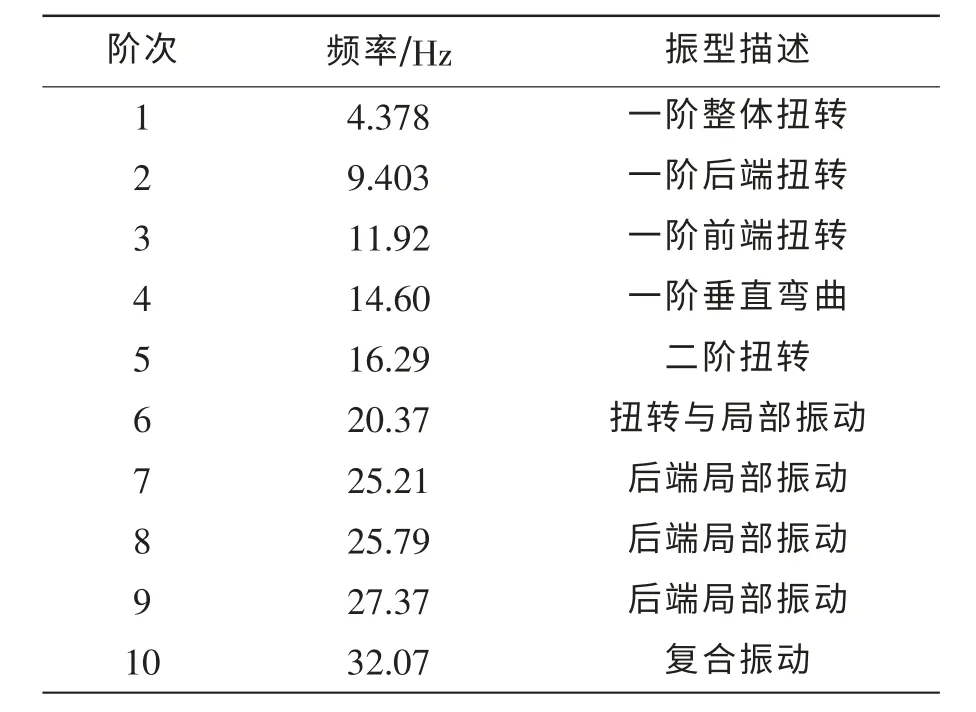
表1 各阶固有频率与振型

4 总结

1）考虑悬架刚度非线性变化因素，建立车架有限元模型，避免了以往忽略或用弹簧单元模拟悬架刚度带来的分析误差。2）满载静止分析表明，车架最大应力值小于许用应力，最大位移在允许变形范围内。因此，车架静强度刚度满足设计要求。3）经典力学方法做了大量简化，计算误差较大，但应力趋势和有限元分析结果一致，表明采用有限元方法分析车架的应力和变形特性是有效的。4）模态分析表明，车架整体扭转刚度较弱，局部振动较明显，因此，应提高整体扭转刚度，并对局部刚度进行加强。

[1]Steve van Herk，Antonia Terzi，Wubbo Ockels.Analysis of lateral dynamics and ride performance of the superbus[C].SAE Paper 2008-01-0586，2008.

[2]钟佩思，赵丹，孙雪颜.基于ANSYS的汽车车架的建模与模态分析[J].机械设计与制造，2008（6）：52-53.

[3]周中坚.机械与汽车构造的有限元分析[M].上海：同济大学出版社，1997.

[4]徐达，蒋崇贤.专用汽车结构与设计[M].北京：北京理工大学出版社，1998：320.

[5]刘鸿文.材料力学[M].上海：高等教育出版社，2001：1740.