矩形大口径弯道空气流量计的压强数值模拟和流量系数研究

李小京，李慧君，张 骏，王 萍

（天津工业大学电气工程与自动化学院，天津 300387）

目前，利用数学模型解决通风管道的流量问题已比较成熟，但是大多数关于空气流量计的研究停留在小口径的圆管和矩形管道上，对于大口径矩形管道的研究相对较少.然而在现实生活中，一些高耗能企业的大型送风系统、大型中央空调送风系统等往往选用口径比较大的矩形管道进行空气输送，而以往对小口径的圆形管道和矩形管道的研究并不适用于大管道矩形送风系统.送风管道中流量参数在整个系统中起着非常大的作用，通过对流量系数的监控，可以判断系统是否正常运行，送风条件是否合理，同时也为我国大气的监控治理提供一定的理论依据.由于企业施工的现场环境往往受到空间的限制，会出现许多弯曲的管道以达到合理的空间利用.本文根据空气流体流经弯道的特点[1]，以不同大口径矩形管道的压强特性为研究对象进行模拟仿真、数据处理[2]，给出流量计流量系数f的合理参考范围.

1 弯道空气流量的理论计算公式

理论上来讲，当气体流经弯道时，由于离心力的作用，会对管径的内外壁产生一个压力差，以往试验研究通过管壁的内外压差可以得到一个弯头流量的理论值公式[3]：

式中：Q为弯道流量计的空气流量（m3/s）；ΔP为弯道内外的侧压力差（Pa）；r为空气密度（kg/m3）；A为弯道的纵截面积（a×b）（m2）；C为相对曲率半径（=R/a）有关系数，C=3.132（）-0.5（2-0.25）ln；如图1所示.系数C的典型值如表1所示.

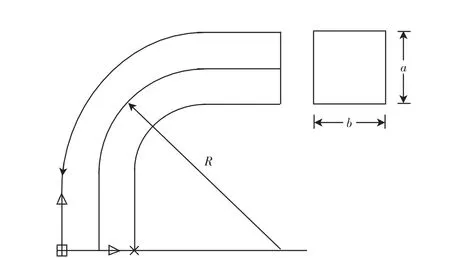
图1 计算示意图Fig.1 Calculation schematic diagram of

表1 系数C的典型值Tab.1 Typical values of coefficient C

2 计算流体力学的求解过程

本文采用Fluent软件进行求解[5].Fluent软件是一款国际上较流行的计算流体动力学（CFD）的商用软件包，主要由解算器Fluent、几何图形模拟以及网格生成预处理程序Gambit和后处理软件Tecplot组成.可用该软件模拟从不可压缩到高度可压缩流体的流动，通过计算机数值计算和图像显示的方法，在时间和空间上描述了流场的数值解，从而达到对流体问题进行研究的目的.求解过程主要包括：控制方程的建立、边界条件与初始条件的确定、计算网格的划分、离散方程的建立、初始条件和边界的离散化、控制参数的求解、离散方程的求解、解的收敛性判断、输出最后的计算结果.

2.1 几何模型的建立

几何模型的建立以物理模型为依据.本实验中管径以矩形管为主，弯道处截面半径分别为1 000、2 000、3 000、3500、4 000 mm，弯道均为90°，相对曲率半径为1.5.纵截面为1 000 mm×400 mm、2 000 m×800 mm、3 000 mm×3 000 mm、3 500 mm×3 500 mm、4 000 mm× 4 000 mm.

2.2 实体模型的建立

利用Gambit软件，在坐标系中确定管道各关键点的坐标，建立点，然后确定线，建立一个平面，由面建立起立体模型.本文以2 000 mm×800 mm为例建模，前后直管段的长度为2 000 mm.

2.3 网格的划分

先确定入口的面，在入口面上均匀划分网格，给定边上的网格数为20，由面的网格确立整个体的网格，最后结果如图2所示.

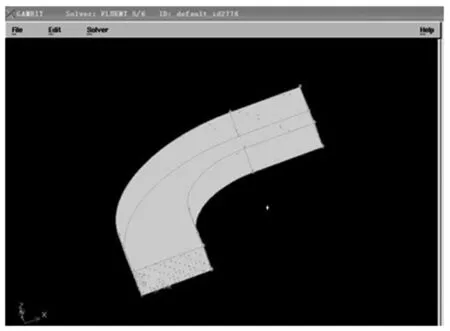
图2 弯道立体图（2 000 mm×800 mm）Fig.2 Bend three-dinensional diagram（2 000 mm×800 mm）

2.4 指定边界条件和区域类型

入口设置为VELOCITY，出口设置为OUTFLOW，其余管道的上下游直管段和弯道内侧为固壁WALL（一般为系统默认）.最后，将网格文件保存输出.

2.5 使用Fluent求解器进行数值计算

在仿真模拟中本文选用的流体为空气，然而流体在流动的过程中并不都是层流，可能出现湍流现象，空气这一流体也不例外.湍流作为一种高度复杂的非线性流动，现已可以通过一些数值方法对其进行模拟，并与实际高度吻合.仿真中主要采用非线性数值模拟，在软件中选择标准k-ε湍流模型[6].

在标准k-ε模型中湍动能k和耗散能ε的输运方程如下：

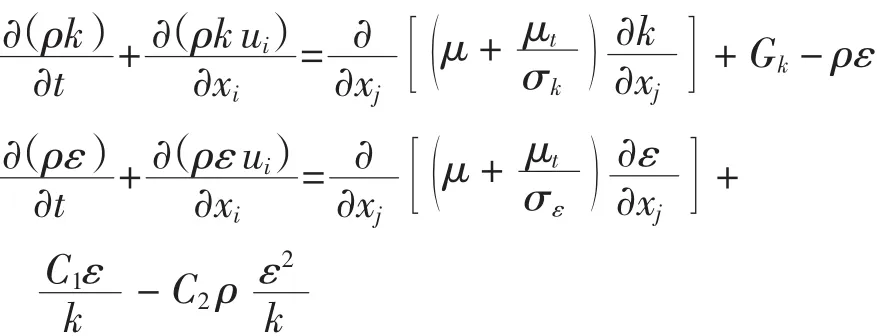
在软件的流体区域，选择空气作为流体，分别给定初始流速10、15、20 m/s，同时定义流体的湍流参数，在这里选择湍流强度和水力直径这两个参数，从而间接给定湍动能k和耗散能ε的值.因为空气属于低湍流强度风洞，自由流的湍流强度通常低于0.05%，这里给定的湍流强度为0.05%；水力直径为4倍的通流截面积除以通流截面的周界长度.

3 压强分布数值模拟

以不同管径的弯道为研究对象进行仿真，根据Fluent软件给出的压强场来说明压强的分布规律.

3.1 压强分布云图

2 000 mm×800 mm弯道的压强云图如图3所示.

图3 2 000 mm×800 mm弯道的压强云图Fig.3 Pressure diagram of 2 000 mm×800 mm bend

由图3可以看出，弯道处压强由内壁面到外壁面逐渐增大，内壁的值为负值，在整个弯道上外壁的压强最大.通过软件本文给出了弯道在0°、22.5°、45°、67.5°和90°纵截面不同高度的压强值[7]，并进行对比，具体角度设计如图4所示.

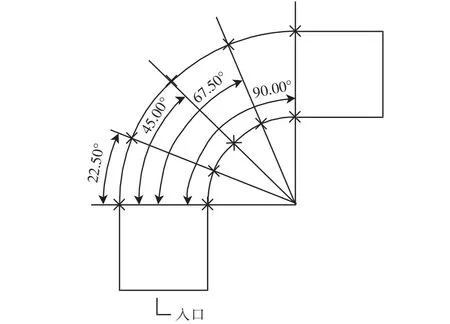
图4 2 000 mm×800 mm管道截面示意图Fig.4 2 000 mm×800 mm pipe section schematic diagram

3.2 弯道断面压强沿程分布

由于需要具体的压强数值进行分析，利用Fluent后处理软件Tecplot进行数据采集，如图5所示.

入口初始给定v=10 m/s时，2 000 mm×800 mm管道在θ=0°、22.5°、45°、67.5°、90°处的压强数值分布结果如图6所示.

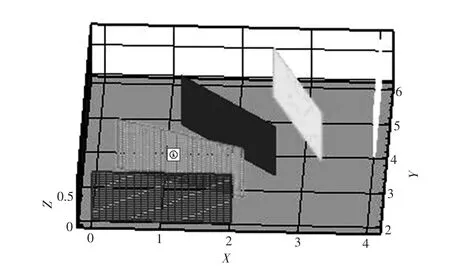
图5 Tecplot中的纵截面切片示意图Fig.5 Schematic diagram of longitudinal section in Tecplot

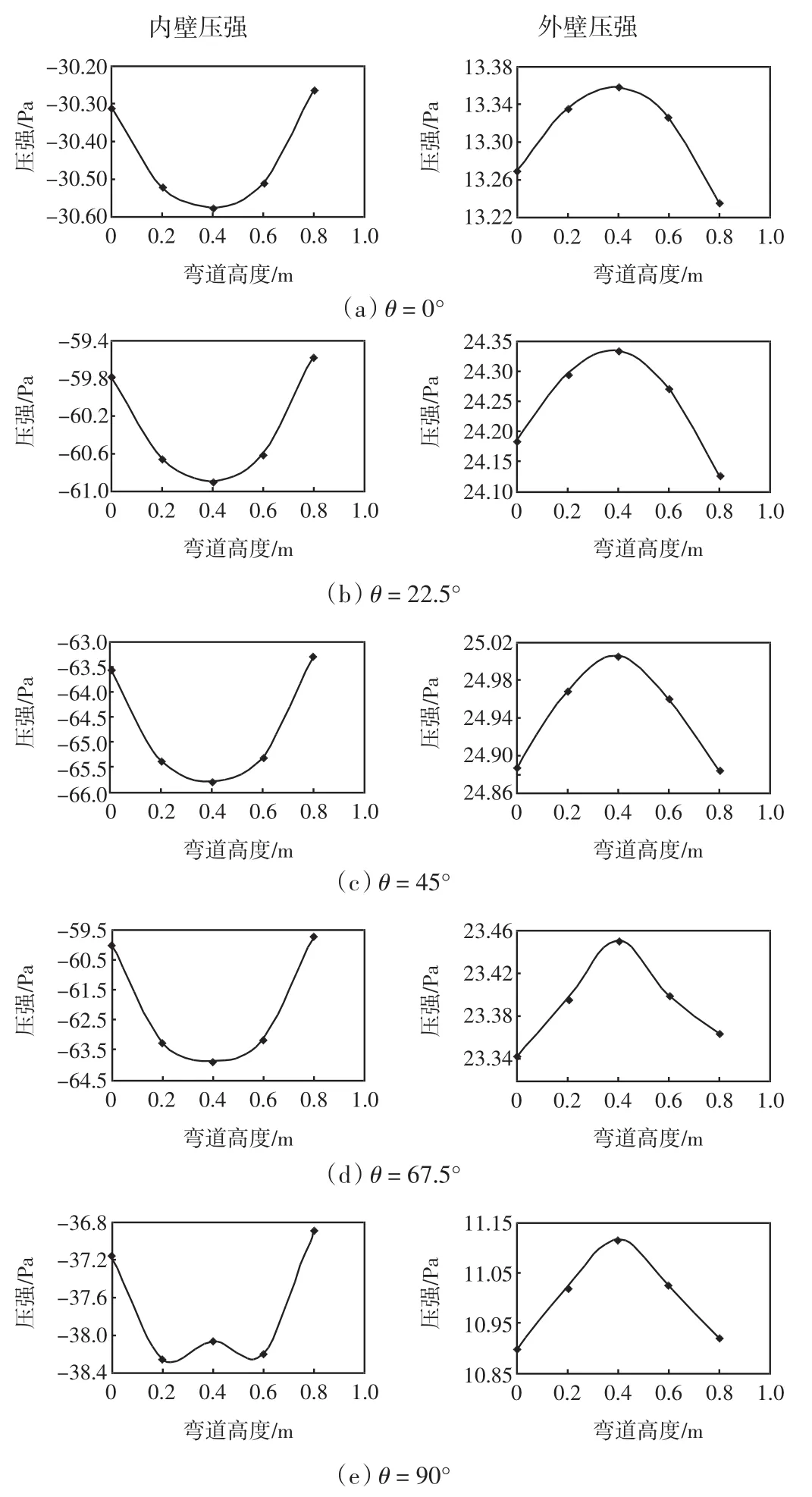
图6 2 000 mm×800 mm管道各截面不同点的压强分布Fig.6 Pressure distribution in different spots of 2 000 mm× 800 mm bend

由图6可知，断面上的压强从弯道的内壁到外壁逐渐增强，与图3的压力云图显示一致；并且在内壁纵截面中点处达到最小值，在外壁纵截面中点处达到最大值，由此可知，各断面中点处的压差最大.在90°的横截面内壁压强并非达到最小值，此口径处为了流量计算的方便就可以不考虑.如果想得到比较大的中点压差值，选45°处的中间点分析最佳，不同纵截面中点的压差值比较如表2所示.

表2 各截面中点处压差Tab.2 Midpoint differential pressure of sections

3.3 不同口径的f值

依据弯道空气流量计流量的理论计算公式以及软件仿真处各断面的内外壁压强差值ΔP和纵截面的流量值Q，可以得出流量系数f值.2 000 mm×800 mm管道中各角度截面的f值如表3所示.

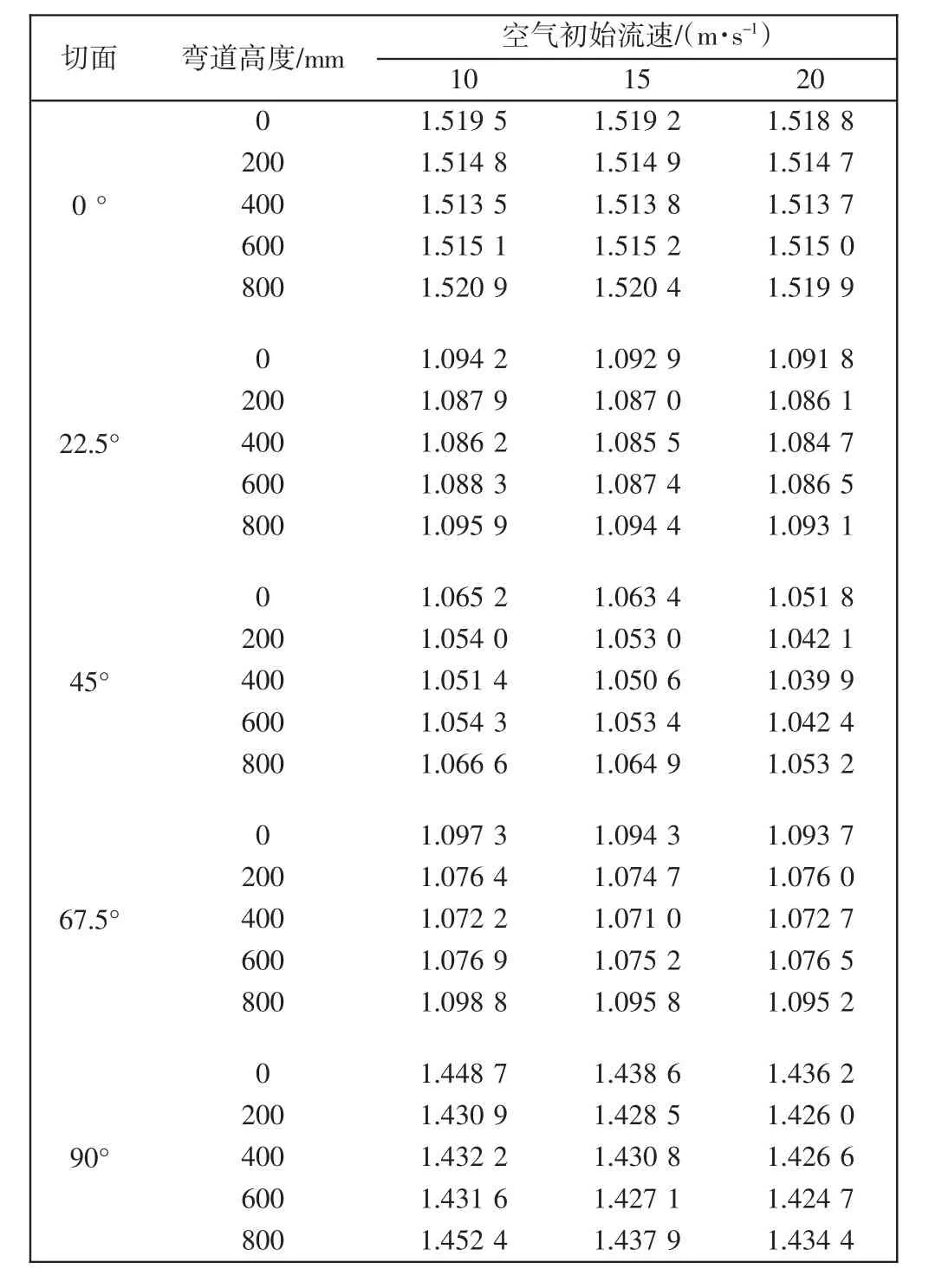
表3 不同截面f值(2 000 mm×800 mm)Tab.3 f value of different sections(2 000 mm×800 mm)

由表3可以看出，相同口径的管道在不同的初始速度下，得到的f值相近，这样通过平均算法就可以得到f的平均值.不同口径的f均值如表4所示.

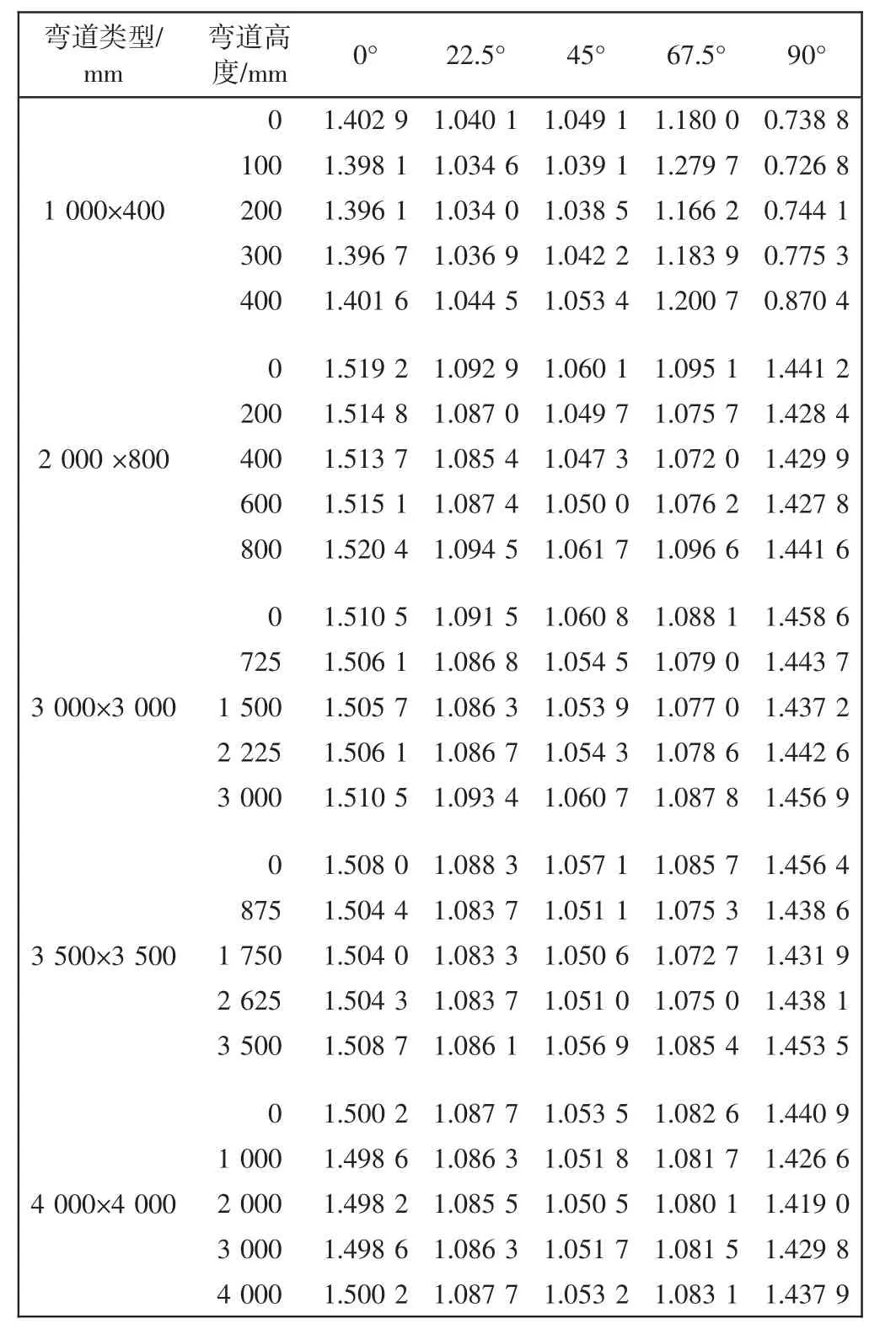
表4 不同口径管道不同切面f值均值表Tab.4 Average f value of different sections in pipes with different diameters apertures

以往对小口径弯道的研究中管道前后长度必须满足一定的条件[8]，才能达到流量检测要求.由表4可以看出，在大口径管道流量的检测上对前后管段的长度并没有硬性要求，在实际应用中可以根据具体位置的需求去安装传感器.

3.4 f值走向及理论公式推导

根据仿真数据结果可以得到f值的大体走向，通过数据拟合可以得到f值在每个切片不同高度位置的理论公式.2 000 mm×800 mm的管道拟合曲线如图7所示.

根据表4实验数据，可以得到不同口径大管道的流量系数f在各切面不同高度的拟合公式，如表5所示.y为f值，x为切面高度，R2为曲线拟合程度指标，其值越接近1则拟合可靠性越高.

图7 f值走向图及数据拟合公式（2 000 mm×800 mm）Fig.7 f values trend chart and data fitting formula（2 000 mm×800 mm）

表5 不同口径f值数据拟合公式Tab.5 f data fitting formula of different aperture

3.5 截面中点处的数值模拟与试验对比

根据之前弯道角度θ=0°、22.5°、45°、67.5°、90°各截面的内外壁压强差对比发现，在45°断面的压差值最大，而且流体动的稳定性最好，实际中以45°中点处作为最佳测压孔进行实际流量系数测量.试验表明口径小的流量系数与实测的流量系数差距较大，口径大的吻合度较好，如表6所示.

表6 流量系数表Tab.6 Flow coefficient table

4 结束语

本文模拟研究了矩形大口径弯道流量计的压强特性.结果表明，由于气体受到离心力的作用,使得弯道中压强由内到外逐步增大，随着弯道纵截面的角度变化，弯道中的压强差先逐步增大然后再逐步减小，在45°中点处达到最大值.仿真中通过对大量的数据进行统计计算，得到了流量系数均值，并通过数据拟合得到一个满足多项式分布的合理f值范围.以上仿真结论均可供实际应用和科学研究参考.

[1]毛新业.矩形大管道的风量测量 [J].自动化仪表，2000，21（3）：11-16.

[2] 孙志强，周孑民，张宏建.弯管流量计测量特性的数值模拟与试验研究[J].传感器技术学报，2007，20（6）：1412-1415.

[3]陆亚俊，李明柱.矩形弯头空气流量计的试验研究-曲率半径的影响[J].建筑技术通讯（暖通空调），1989（6）：42-45.

[4]陆亚俊，李明柱.矩形弯头空气流量计的试验研究—流量系数的推荐值[J].通风除尘，1988（2）：5-9.

[5] 周俊杰，徐国权，张华俊.Fluent工程技术与实例分析[M].北京：中国水利水电出版社，2010.

[6] 于勇.Fluent入门与进阶教程[M].北京：北京理工大学出版社，2008.

[7] 王晓禹，李玉凤，李志.弯管流量计取压孔实验研究[J].计量技术，2008（5）：3-5.

[8] 李少峰，薛贵军，孟宪举，等.高精度弯管流量计的理论研究和实验验证[J].计量学报，2013，34（2）：1111-1116.