基于EMD方法的心电信号带内噪声滤除

刘萌萌，王 敏，熊 慧，董 锟，韩 帅

（天津工业大学电气工程与自动化学院，天津 300387）

心电信号（Electrocardiogram，ECG）是心脏的电活动在体表的表现，包含着人体大量的生理或病理信息，是一种重要的生物电信号.心电信号又是一种低幅值、低频率、低信噪比同时伴随着各种干扰的随机性很强的非线性、非平稳信号，且噪声与心电信号存在时频重叠[1]，致使心电信号的滤波去噪变得复杂困难.传统的傅氏变换是以平稳性假设为前提的纯频域或时域的全局变换，不能反映信号指定时刻的时频变化特性，对心电信号的分析有局限性[2].小波变换同时具备时域和频域局部化的特性，适用于分析非平稳信号，因此在心电信号的处理中得到了广泛的应用[3-6].但是，小波变换存在许多不足，如小波基的选择缺乏自适应性，去噪时阈值的选取也很困难等[7].1998年，Huang等[8]提出经验模态分解（empirical mode decomposition，EMD）算法，EMD是一种新的特别适合非线性、非平稳时间序列分析处理的自适应时频分析方法，已在工程领域得到了广泛的应用[9].EMD方法主要是基于信号自身的局部特征时间尺度，将信号自适应地分解成若干个频率从高到低排列的本征模态函数（intrinsic mode function，IMF），并且每个IMF分量都具有瞬时频率的物理意义.利用EMD方法去噪时，可以根据信号的频带，对IMF分量进行阈值量化重构信号.文献[2]中应用此阈值方法去噪时，发现重构信号有较大偏差，信号失真；EMD阈值法适合滤除带外噪声[10]，当信号频带与噪声频带有重叠时，滤波效果不理想.本文通过分析EMD算法分解出的心电信号各IMF分量频带的特点，研究随机噪声的特性，提出用基于EMD的方法滤除心电信号的带内噪声.用这种方法处理实际采集的心电数据时发现，在保证有用信号完整性的前提下，不仅达到了去噪目的，同时也提高了信噪比，验证了该方法处理心电信号的有效性.

1 基于EMD的信号带内噪声去噪原理

任何复杂信号都由若干个互相独立的简单信号构成，采用合适的处理方法可将各单分量信号分离出来.EMD方法正是在这种基础上提出的，它是一种新型的、基于信号自身特征的时频分析方法，适用于非线性、非平稳信号的分析处理.EMD算法的原理和具体分解步骤参考文献[8].

微弱信号的检测和处理主要针对的是噪声信号，并且绝大部分为随机噪声，随机噪声是现阶段技术发展的主要障碍[11].通常对微弱信号检测时，要经过一定的电路处理，如信号放大、AD转换等.因此，在信号的整个传输过程中会引入一定的随机噪声.随机噪声任何时刻的幅值、相位及波形都是随机变化的，不能用确定的幅值谱和确定的时间函数表征[12]，但功率谱可以反应信号的功率密度随信号频率变化的情况，因此可以用功率谱函数来描述它的频域特性[13].所以，对含噪信号噪声频率的分析就可以转化为对其功率的分析.假设实测信号在频率f处对应的功率为P（f），其中参杂着的随机噪声的功率为σ2，则实测信号的功率[14]为Pm（f）：

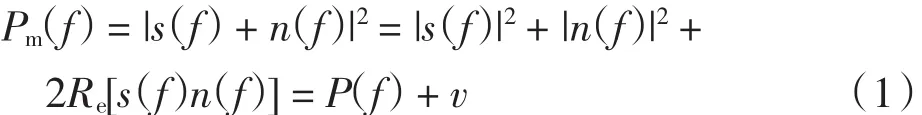
式中：s（f）为频率f处的理论信号；n（f）为频率f处的噪声信号；Re表示取函数的实部；v记为实测信号中随机噪声引起的误差，其大小为|n（f）|2+2Re[s（f）n（f）].若某频率或某频带范围的噪声较大，相应的v也会较大.若v很小，实测信号的功率与理论信号的功率基本相等，则基本达到了去噪的目的.

EMD算法可将任一非线性、非平稳信号分解成固定个IMF分量和一个趋势项，并且每个IMF分量对应信号的某频带.对含噪信号s（t）进行EMD分解，得到有限个频带从高到低排列的IMF分量和一个趋势项，若把趋势项记为第n个IMF分量，根据EMD算法的完备性：

式中：阶数低的IMF分量是信号的高频分量，一般是有用信号频带和噪声频带重叠的分量，特别是第一个IMF分量.根据噪声的统计特性，当对噪声采样点的位置进行随机排序而保持对应位置噪声分量的幅值不变时，噪声的总功率也保持不变.将同时含有用信号和噪声信号的IMF分量按照基于噪声统计特性的原理进行随机排序得到一个新的分量IMF1，用IMF1与其余的（n-1）个IMF分量重构信号s1（t），s1（t）仍满足算法的完备性要求，并且s1（t）的功率不变；重复操作，对含噪分量随机排序N次得重构信号sn（t），信号s（t），s1（t）…sn（t）共（N+1）个信号，对这（N+1）个信号累加取平均：

相对于信号s（t），sav（t）噪声的分量理论上削弱为原来的1/（N+1），而有用信号的功率基本保持没变.当N大到一定程度时，sav（t）中噪声的含量基本可以忽略.因此，达到去噪目的.并且这种方法仅使噪声的功率在很大程度上被消弱，而有用信号的功率基本保持不变，这在一定意义上保证了有用信号的完整性.sav（t）是去噪后信噪比被提高的“干净”信号.

2 实验与结果分析

2.1 标准心电信号实验与分析

为了验证基于EMD的信号带内噪声去噪方法对心电信号处理的有效性，并验证该方法适合于低信噪比的微弱信号的检测，本文以MATLAB软件为处理工具，对美国哈佛大学ATM医疗数据库的标准心电信号进行实验验证.标准心电信号的采样频率为250 Hz，数据长度为1 024个采样点.从对加噪标准心电信号去噪前后的波形及信噪比（signal noise ratio，SNR）的变化两个方面来评价算法的有效性.

图1所示为去噪前后的心电信号波形对比.

心电信号的频率在0.05~100 Hz范围内，但其频谱能量却主要集中在0.25~35 Hz范围内.当对标准心电信号加随机噪声时，噪声信号随机分布在心电信号的频带范围内，使心电信号和噪声信号相互重叠.由图1可以看出，用EMD阈值法处理含噪信号时（图1（c）），在滤除噪声的同时也去掉了部分有用信号，信号的波峰在较大程度上衰减，部分最大值小于0.5 mV，波形失真较严重；而采用本文方法去噪后（图1（d）），最大波峰虽然也有些衰减，但其峰值仍大于0.5 mV，并且心电信号的某些特征点也被有效地保留了下来.由图1（c）、（d）对比可见，本文提出的基于EMD的信号带内噪声去噪方法在对低信噪比的心电信号去噪时的效果较好.

图1 去噪前后波形对比Fig.1 Waveforms comparison before and after de-noising

表1所示为几组标准心电信号加白噪声后，经EMD阈值去噪和基于EMD的信号带内噪声去噪后所得信噪比的对比.

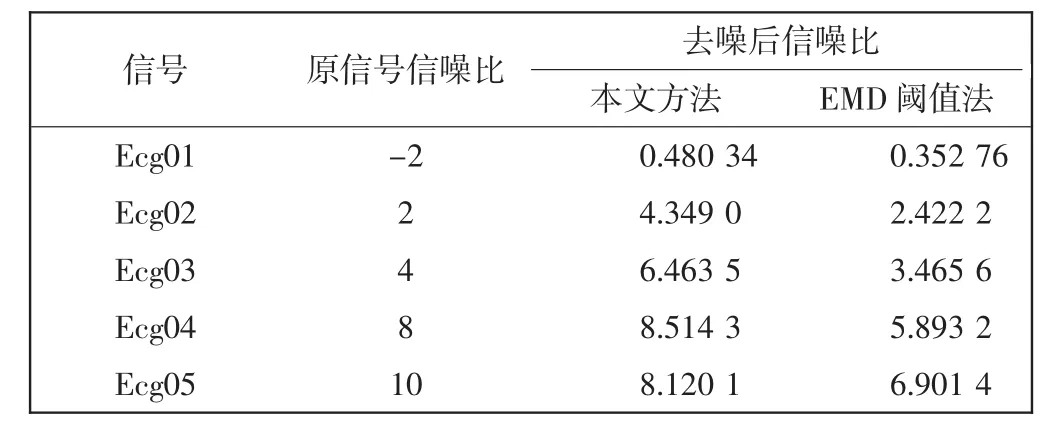
表1 2种方法去噪后信噪比的比较Tab.1 SNR comparison after de-noising with two methods

由表1可以看出，对信噪比为2的含噪信号进行去噪处理，EMD阈值法得到的信噪比为2.422 2，而本文提出的基于EMD的信号带内噪声去噪方法得到的信噪比为4.349.由此说明，对相同低信噪比的含噪信号进行去噪处理，采用本文方法能更大地提高信号的信噪比.

2.2 实际采集心电信号的试验与分析

为了验证本文算法的实用性，对实际采集的心电信号采用本文算法进行处理分析.

体表电极采得的电信号，其幅值至多是mV数量级，频率范围一般在0.05~100 Hz.心电信号的采集过程易受50 Hz工频干扰、肌电干扰、电极极化电压干扰及基线漂移的干扰等[15].因此，实际心电信号会不可避免地含有噪声干扰，使有用信号淹没在噪声中，信号的信噪比较低，信号波形不明显.

实验室心电信号的采集系统是基于PSoC3开发套件设计的.采集系统以PSoC3自带的8051 MCU为主控器件，设计中用到的运算放大器Opamp、12位差分A/D、定时器Timer和串口模块UART都由PSoC原器件库提供.它们在PSoC原理图上直接配置、连接，省去了外部布线，使电路更方便、灵活，同时也减少了外电路接线的复杂性及部分外部干扰.实验的心电信号是Ⅲ导联采集的人体心电信号，信号的采样频率fs= 300 Hz，采样点数N=1 024个，信号波形及频谱图如图2所示.

图2 实测原始心电信号的波形及频谱图Fig.2 Waveform and frequency spectrum of measured original ECG signal

对图2所示心电信号进行EMD分解，分解结果如图3所示.

由图3所示EMD分解得到的13个IMF分量中可以看出，第一个IMF分量为高频成分，其余的IMFs分量按频率从高到低依次排列，均代表了心电信号中各频带的有效信息.针对实测心电数据EMD分解的结果，分别采用EMD阈值法和基于EMD的信号带内噪声滤除法进行处理，结果如图4所示.

由图4可知，虽然采用本文方法去噪后的信号中还有噪声成分，但相对于有用信号，所占比重几乎可以忽略，特别是去噪前后50 Hz工频干扰噪声含量的对比.并且这种去噪方法并没有像EMD阈值法那样，把含有用信号的噪声成分直接去除，而是消弱了噪声在整个信号中的含量，保留了噪声中的有用信号，即保留了有用信号的完整性.对比两种方法去噪后的波形可以看出，EMD阈值法由于去掉了部分有用信号，波形失真.对比分析可见，基于EMD的信号带内噪声去噪法更适合心电信号的处理.

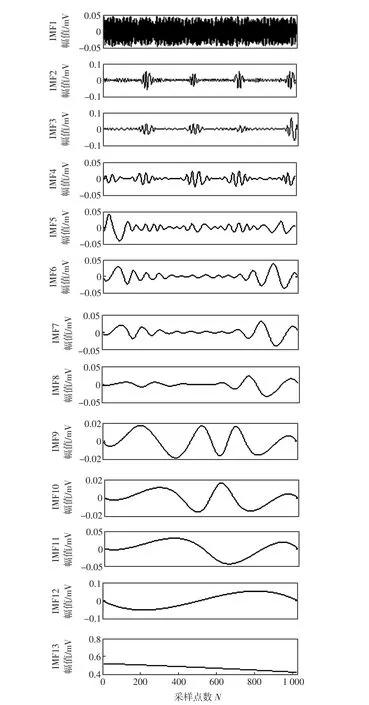
图3 实测信号的EMD分解结果Fig.3 EMD decomposition of measured signal

图4 两种方法对比Fig.4 Comparison of two methods

3 结束语

EMD方法是一种有效的非线性、非平稳信号处理方法，本文提出用基于EMD的信号带内噪声去噪的方法处理心电信号，并对实测心电数据进行了实验与分析，验证了算法的有效性.与传统的EMD阈值算法相比，本文方法仅对含噪的IMF分量用基于噪声统计特性的理论进行随机排序，没有直接去掉含噪部分，而是保留了含噪分量的有用信号，其去噪效果明显优于EMD阈值法.这种方法更适合用于噪声与有用信号频带混叠的信号的去噪.

[1] 王芳，季忠，彭承琳.基于双树复小波变换的心电信号去噪研究[J].仪器仪表学报，2013，34（5）：1160-1165.

[2] 邹清，汤井田，唐艳.Hilbert-Huang变换应用于心电信号消噪[J].中国医学物理学杂志，2007，24（4）：309-312.

[3]MARTINEZ J P，ALMEIDA R，OLMOS S，et al.A waveletbased ECG delineator：Evaluation on standard databases[J]. IEEE Transactions on Biomedical Engineering，2004，51（4）：570-581.

[4]KANIA M，FERENIEC M，MANIEWSKI R.Wavelet denoising for multi-lead high resolution ECG signals[J].Measurement Science Review，2007，7（2）：30-33.

[5] POORNACHANDRA S.Wavelet based denoising using subband dependent threshold for ECG signals[J].Digital Signal Processing，2008，18（1）：49-55.

[6]吕振肃，马文.自适应小波阈值算法在心电信号去噪中的应用[J].数据采集与处理，2009，24（3）：313-317.

[7] TSE P，YANG W X，TAM H Y.Machine fault diagnosis through an effective exact wavelet analysis[J].Journal of Sound and Vibration，2004，277（5）：1005-1024.

[8] HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition method and the hilbert spectrum for non-stationarytimeseries analysis[J].Proc Royal Soc London A，1998，454：903-995.

[9]刘立君，王奇，杨克己，等.基于EMD和频谱校正的故障诊断方法[J].仪器仪表学报，2011，32（6）：1278-1283.

[10]王英，曾光宇.基于小波的EMD去噪法应用于心电信号去噪[J].数值计算与计算机应用，2011，32（4）：274-282.

[11]MOON J，NO J，LEE S，et al.Noise and interference characterization for MLC Flash memories[C]//2012 International Conference on Computing，Networking and Communications（ICNC）.Maui：IEEE，2012：588-592.

[12]VASS P.Random noise reduction capability of the Hermit polynomial based least squares fourier transform method[J]. Acta Geodaetica et Geophysica Hungarica，2012，47（3）：328-343.

[13]BENDAT J S.Principles and applications of random noise theory[M].New York：Wiley，1958.

[14]吴雪梅，娄珀瑜.论随机噪声对光谱测量的影响[J].计算机与应用化学，2011，28（10）：1343-1345.

[15]李雪飞，毛玉星，何为，等.提升小波和平滑滤波在心电信号快速滤波中的研究[J].生物医学工程学杂志，2008，25（1）：191-195.