改进灰色证据理论的区间数决策方法研究

李存斌，赵 坤，2，苑嘉航

（1.华北电力大学经济与管理学院，北京 102206；2.国华能源投资有限公司，北京 100007）

多指标决策是一种基于多个指标属性的情况下，选择最优方案排序的问题，其在实际生活中有着广泛的应用[1].由于客观世界的复杂性和人类认知的主观不确定性，人们对事物的内部发展变化规律不能给出合理的解释.当面临一些多指标决策问题时，对指标的描述往往也是模糊的、不精确的、灰色的.这种不精确的描述信息常常不是用实数来简单表示，而是用区间数的形式来表达.因此，对于决策指标值为区间数、决策指标权重为区间数的多指标决策问题也引起了广泛的关注[2-4].Zhang等[5]在区间数向量范数应用的基础上，提出了使用灰色关联分析区间数多指标决策；刘勇等[6]结合灰靶模型与前景理论，考虑决策人的风险态度，提出了一种区间数的多目标决策方法；王坚强等[7]扩展了区间数的范围，提出了区间灰色区间数，并针对其多准则决策问题，提出了灰色模糊的决策方法；Jahanshahloo等[8]扩展了TOPSIS的应用范围，利用相似理想解排序进行多指标区间数的决策.由于灰色关联具有样本数据少、易结合的优点，上述文献在研究中都成功地借鉴了灰色关联理论，但却忽略了决策过程中不确定性的问题.从不确定性的角度考虑，推理决策方法适合处理不确定性信息，提高决策能力.证据理论作为一种不确定性的推理方法，已被一些学者应用于决策领域中.潘巍[9]等分析比较了证据理论的决策规则，并提出了基于pignistic概率的决策规则.陈增明[10]把证据理论应用于群决策中，并对个体决策结果一致性分析方法进行了研究.虽然证据理论可以有效地处理不确定信息，但它也要求了证据之间的相互独立性，因此也存在着无法处理冲突证据和基本概率赋值获取困难的局限[11].许多学者对证据理论算法进行了改进，大致可以分为2种：①修改合成过程.如孙全等[12]针对证据合成中的悖论问题和改进后的Yager受限制的问题，在应用证据理论中可信度概念的基础上，提出了新的合成公式.②修改证据源.王育红等[13]通过理想属性偏离度把区间数决策问题转化成了确定性的决策问题，将灰色关联分析法与D-S证据理论相结合，提出了信息不确定的提取方法和Mass函数，并研究了不同子集间信度函数和Mass函数之间的关系.李鹏[14]将区间数的决策问题扩展为区间直觉模糊数的决策问题，根据决策者的风险态度，定义了转化算子，利用灰色关联分析法从新定义了指标的不确信度，进而得到不同于王育红的Mass函数.改进的方法虽然很好地结合了灰色关联和证据理论，明显降低了融合后的整体不确信度，但仍存在一些不足.以上研究均通过各自的定义将区间数转化成实数进行后面的计算，但是实数作为一个精确值，过早地被运用于计算指标不确信度，会造成原本的区间数表达的信息丢失.而指标的不确信度是构建Mass函数的重要基础，如果它的值不准确会使融合结果中的整体不确定性增加，从而导致融合结果不准确.在灰色关联结合证据理论的决策问题中，虽然有研究考虑了指标权重（决策者对于指标的偏好）的影响[15]，但是没有研究将区间数决策问题中的指标权重纳入Mass函数中，以致决策结果忽略了各指标权重的影响.基于上述分析，本文在王育红等的研究成果基础上，将灰色关联和证据理论结合用于区间数决策问题中.引用定义理想距离矩阵，通过区分效益型指标和风险型指标确定了规范化决策矩阵，利用区间数熵权法求出指标的客观权重，使用灰色关联法分析加权区间数之间的距离，求出指标的不确信度，结合理想偏离度矩阵构建Mass函数，最后利用证据理论进行信息融合，并与借鉴的成果相对比，得到了更为满意的结果.

1 区间数及D-S证据理论

1.1 区间数的基本知识

设两个区间数s1= [s1l，s1u]（s1l＜s1u） 和s2=[s2l，s2u]（s2l＜s2u），区间数的四则运算规则如下[16]：

s1+s2=[s1l+s2l，s1u+s2u]

s1×s2=[s1l×s2l，s1u×s2u]

定义1[17]两个区间数的距离公式为：

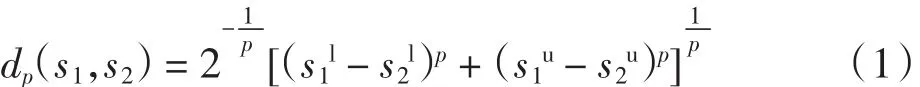
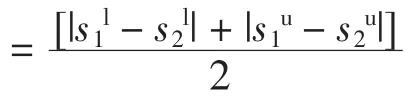
定义2[18]区间数s1≥s2的可能度为：

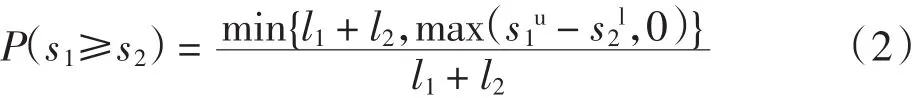
式中：l1=s1u-s1l，l2=s2u-s2l，0≤P（s1≥s2）≤1.如果0.5≤P（s1≥s2）≤1，则判定s1≥s2；否则，s1＜s2.区间数越大，表明属性属于该评判等级的概率越高[19]. 1.2 区间数熵权法

指标权重的确定方法归纳起来包括主观赋权方法、客观赋权方法和主客观赋权结合的方法.主观赋权方法通过调研相关领域的多名专家根据其知识能力和工作经验对指标权重进行主观判断，并采用数学方法将指标权重量化表示，如AHP、ANP、三角模糊数、梯形相似模糊数等.客观赋权方法依据决策矩阵中各个备选方案的指标值差异程度进行客观赋权.客观赋权法适用于多指标决策时指标权重无明显偏好的问题，采用客观方法可以有效避免主观赋权时权重所产生的主观性，如离差最大化、理想偏离、熵权法等.主客观赋权结合的方法主要是利用上述方法将决策问题的主观权重和客观权重分别求出，再通过离差最大化设定权重系数，最后的权重为主客观的线性结合.针对区间数多指标决策问题的权重确定方法，为避免主观赋权方法对决策结果对比的影响，本文采用客观赋权法.而鉴于离差最大化和理想偏离方法赋权时的一些不足，本文借鉴文献[20]的研究成果，利用熵权法计算指标值为区间数的指标权重.

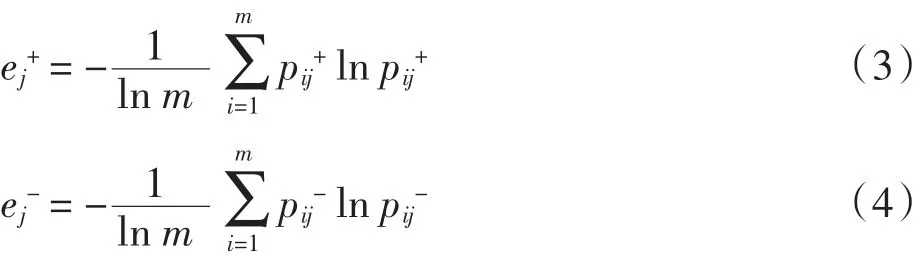
设上下界信息熵的平均值ej可以表示指标Ij下各个备选方案区间数的偏差程度，则ej为Ij下各个备选方案区间数指标值的信息熵.

ej最大值为1，熵值最大时，指标对整体的贡献最小，指标Ij下备选方案的重要程度越小，即相应的权重也越小，此时可用1-ej度量其重要程度，则区间数指标Ij的权重为：

1.3 D-S证据理论

D-S（dempster-shafer）证据理论是一种不确定性推理融合算法，它利用不确定性的评判和推断，对评判和推断中的一致性信息进行聚焦，对矛盾信息进行删除和从新整合，最后得到结论[22].由于证据理论中需要的先验数据相比于概率论中的推理等更容易获得，且其核心算法Dempster合成规则可以融合不同信息源的数据，使得证据理论在情报分析、威胁评估、风险诊断、多属性决策等多领域有着广泛的应用.

定义3 识别框架Θ，识别框架是一个互斥非空有限集合，表示对整体的判断，框架内包含了对某事件推断的所有可能假设.

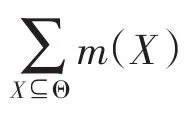
区间的上限称为似然函数 （plausibility function，pl），在识别框架Θ上似然函数定义为：

某假设的信任函数bel（A）和似然函数pl（A）组成信任区间[bel（A），pl（A）]，可以用来表示对这个假设的确认程度，如图1所示.

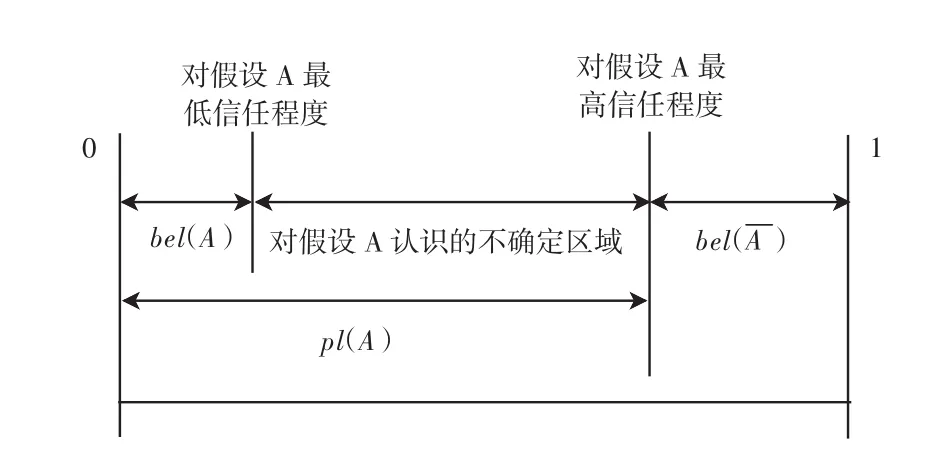
图1 信任函数与似然函数的关系Fig.1 Relationship between belief function and plausibility function

由图1可以看出：

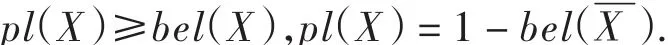
Dempster合成规则也称证据合成公式，如式（9）所示：

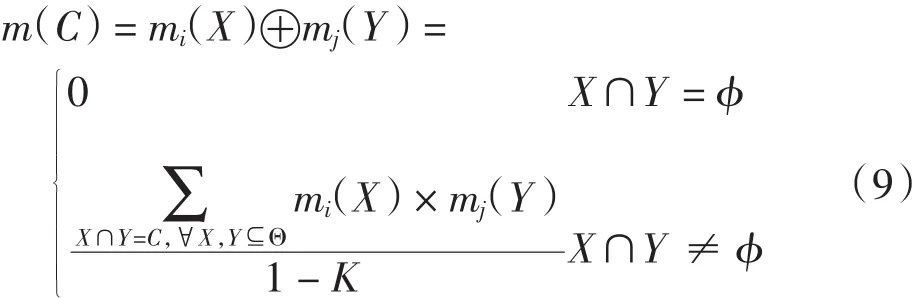
对于识别框架Θ下n个证据m1，m2，…，mn的合成规则[13]如式（10）所示：

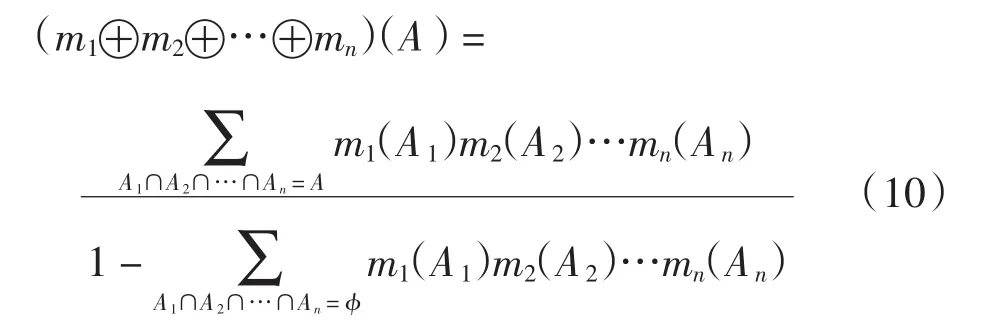
式中：A⊆Θ，m1，m2，…，mn为识别框架Θ上的Mass函数.

D-S证据理论合成公式有交换性和结合性两个重要特征.具体表述如下：

（1）m1⊕m2=m2⊕m1；

（2）m1⊕（m2⊕m3）=（m1⊕m2）⊕m3.

2 决策模型

2.1 区间数规范化与理想距离

针对某决策问题有m个备选方案，S=（S1，S2，…，Sm），对于方案的决策属性有相应的n个评判指标，I=（I1，I2，…，In）.备选方案在指标下的值为sij，且sij=[sijl，siju]是一个区间数，0≤sijl≤siju，当sijl=siju时，区间数就会退化为实数，由sij构成了初始的区间决策矩阵S=（sij）m×n.由于各指标的属性不同，为了消除不同量纲对决策结果的影响，使指标属性统一，需要对初始区间决策矩阵进行规范化处理，得到规范化区间矩阵S=（sij）m×n，sij=[sijl，siju].首先将指标属性分类，分为效益型指标和风险型指标.对于效益型指标，有

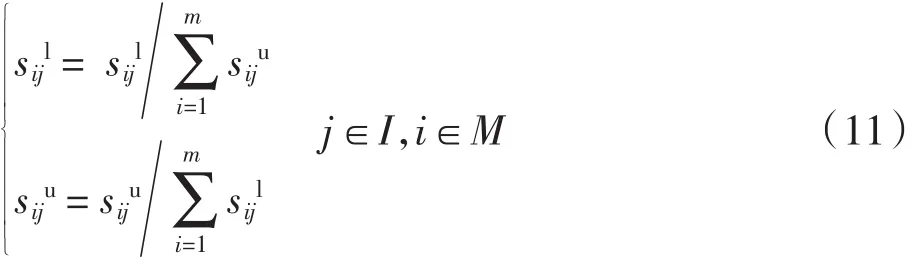
对于风险型指标，有

根据区间数熵权法的权重ωj，得到加权区间数决策矩阵X=ωj×Sij=ωj×[sijl，siju]m×n=[xijl，xiju]m×n

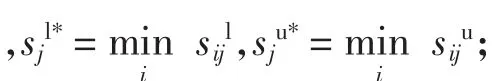
通过区间数距离公式（1），计算各指标值关于理想区间数的距离d，令gij=d（sij，sj*），构建理想距离矩阵G=（gij）m×n.如果距离越大，说明该指标值与设定的理想区间的偏差就越大，那么该指标值在决策过程中被视为较佳的选项.反之，则被视为较差的选项.

2.2 改进的灰色Mass函数

确定指标的不确信度是得到多方案Mass函数的关键，为避免区间数转化中原有的信息丢失，本文以原决策矩阵中区间指标值为基础，运用灰关联法来计算指标的不确信度.

指标Ij的q阶不确信度为：

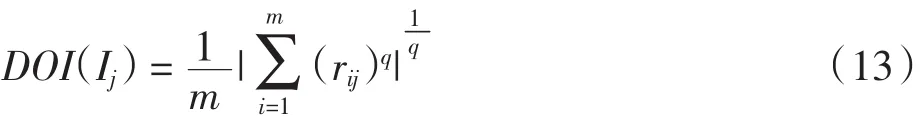
式中：q=2；rij为综合灰关联系数，rij=1/（1+rij+/rij-）2；rij+为最优关联系数；rij-为最劣关联系数.使用最优最劣两个关联系数求解可以提高结果的准确性，避免结果失真.

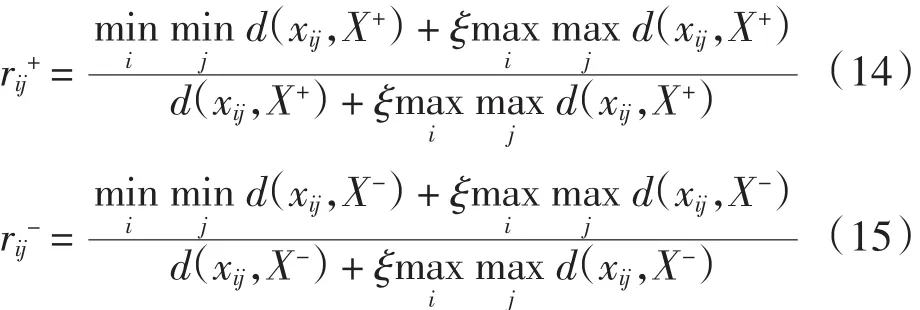
在确定各指标的不确信度后，通过公式（7）计算各指标基本概率分配：

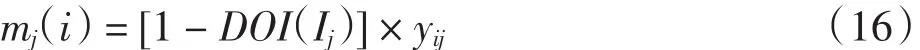
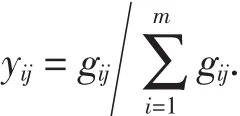
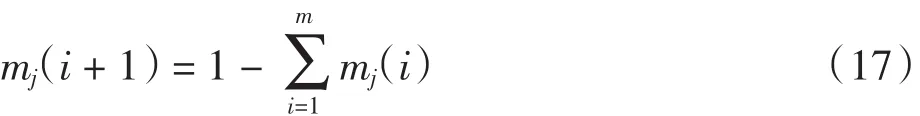
3 决策步骤

综上所示，可以得到改进灰色关联和D-S证据理论的决策步骤.

（1）确定初始风险矩阵Sij=（sij）m×n=[sijl，siju]m×n，判断指标的属性，通过公式（11）和（12）求出规范化决策矩阵Sij=（sij）m×n=[sijl，siju]m×n.通过距离公式求出Sij与各指标下的理想区间数的距离矩阵G=（gij）m×n，标准化后得Y=（yij）m×n.

（2）应用区间熵权理论，求得各指标的权重ωj（j= 1，2，…，n）.得到加权风险矩阵X=ω×Sij=[xijl，xiju]m×n.

（3）判断加权决策矩阵中的最优理想序列和最劣理想序列，通过公式（14）和（15）确定最优关联系数矩阵和最劣关联系数矩阵，进而得到综合关联系数矩阵，由公式（13）得到指标Ij下的不确信度DOI（Ij）.

（4）由公式（16）计算Mass函数mj（i）并确定整体不确定的Mass函数mj（i+1）.

（5）应用公式（10）进行Mass函数的合成，得到证据对各方案的置信度，对备选方案进行排序得出结论.

4 算例分析

本文为了证明提出的改进有效，引用文献[13]的算例，并与之前的算法进行对比.有房地产的投资决策方案S={S1，S2，S3，S4}.该投资项目有5个评价指标I1、I2、I3、I4、I5分别表示房屋的面积、设施水平、小区环境、房屋价格和小区与工作单位的距离.其中房屋的面积、设施水平、小区环境为效益型指标，房屋价格和小区与工作单位的距离是风险型指标.4种投资方案的初始决策区间值如表1所示.

表1 各方案的初始指标值Tab.1 Initial index value of each project

根据公式（11）和（12）对初始矩阵进行规范化处理，得到规范化区间值如表2所示.

利用区间熵权法求解指标的权重，首先要求得各个方案指标值的上界和下界决策矩阵：

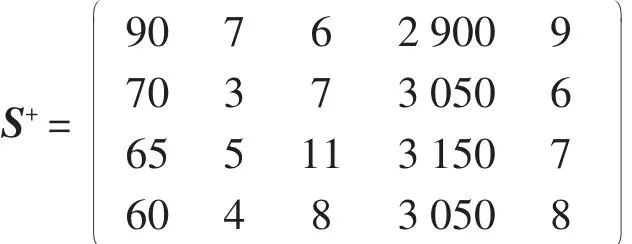
下界序列信息熵：e1-=0.991 1，e2-=0.965 6，e3-= 0.981 0，e4-=0.999 6，e5-=0.991 9.上界序列信息熵：e1+=0.987 8，e2+=0.968 0，e3+=0.988 4，e4+=0.999 7，e5+=0.993 1.通过公式（6）计算决策方案中各指标的权重：ω1=0.193 6，ω2=0.507 9，ω3=0.184 1，ω4= 0.004 7，ω5=0.109 5.

通过对各个区间数的距离判断，找出最优理想区间序列和最劣理想区间序列，通过公式（14）和（15）求出最优关联系数矩阵Rij+和最劣关联系数矩阵Rij-，并求出综合关联系数矩阵R.

各指标的不确信度为：

DOI（I1）=0.218 8，DOI（I2）=0.173 3，DOI（I3）= 0.191 8，DOI（I4）=0.162 7.根据定义的理想区间数，得到理想偏离度矩阵和标准化决策矩阵Y=（yij）m×n，构建整体不确定的Mass函数：

在Mass函数矩阵中，整体不确定性的Mass函数为：m1（5）=0.218 8，m2（5）=0.173 2，m3（5）=0.191 7，m4（5）=0.162 7，m5（5）=0.180 6.令Θ={S1，S2，S3，S4}，并取2Θ={{S1}，{S2}，{S3}，{S4}，{S1，S2，S3，S4}}，通过D-S证据理论合成Θ中各子集的信度函数：

bel（A1）=（m1⊕m2⊕m3⊕m4⊕m5）（A1）=0.415 5

bel（A2）=（m1⊕m2⊕m3⊕m4⊕m5）（A2）=0.276 9

表2 规范化后的各方案指标值Tab.2 Standard index value of each project

bel（A3）=（m1⊕m2⊕m3⊕m4⊕m5）（A3）=0.253 9

bel（A4）=（m1⊕m2⊕m3⊕m4⊕m5）（A4）=0.047 2

bel（A1，A2，A3，A4）=（m1⊕m2⊕m3⊕m4⊕m5）（A1，A2，A3，A4）=0.006 4

根据信度函数最大化的原则，决策者在风险中性的态度（即没有主观权重）下应选取S1方案，4个备选方案的选择排序应为S1＞S2＞S3＞S4，在信息融合之后，整体不确定性的信度函数值由最初的18.66%下降到0.64%.原文结果与本文结果的对比如表3所示.

表3 原文结果与本文结果的对比Tab.3 Comparison of previous and this paper′s results %

由表3可知，对比于原文献中的结果，方案排序选择相同，但本文的初始指标不确定性（平均值18.66%）和整体不确定性（0.64%）都大幅度降低，而且融合结果中方案的优劣也较前文更明显.方案1的信度增加（原文结果为36.43%）；而方案4的信度降低（原文结果为7.5%）；方案2和方案3之间的差距也较原文结果有所拉大，说明方案2优于方案3.融合结果更有利于决策者做出决策.

5 结束语

本文对灰色关联和D-S证据理论相结合的区间数决策方法进行改进，区分决策中效益型指标和风险型指标，规范化决策矩阵，利用区间熵权法求出权重，并代入决策矩阵中，通过加权区间数矩阵求出指标不确信度.由理想偏离度矩阵和指标不确信度构建Mass函数，最终应用Dempster合成法则对信息进行融合.对比之下，改进的结果降低了整体不确信度，增加了各方案置信度的差距，更为符合决策者的需求，更利于投资者进行决策.

[1] HWANG C L，YOON K.Multiple Attribute Decision Making：Methods and Applications[M].New York：Springer-Verlag，1981.

[2]LAKSHMANA G N V，MURALI Krishnan S，SIVARAMAN G.Multi criteria decision making method based on intervalvalued intuitionistic fuzzy sets[J].Expert Systems with Applications，2011，38（3）：1464-1467.

[3] XU Z S.A method based on distance measure for interval-valued intuitionistic fuzzy group decision making[J].Information Sciences，2010，180（1）：181-190.

[4] WU J，FRANCISCO C.Non-dominance and attitudinal prioritization methods for intuitionistic and interval-valued intuitionistic fuzzy preference relations[J].Expert System with Applications，2012，39（18）：13409-13416.

[5] ZHANG J J，WU D S，OLSON D L.The method of grey related analysis to multiple attribute decision making problems with interval numbers[J].Mathematical and Computer Modelling，2005，42：991-998.

[6] 刘勇，FORREST Jeffrey，刘思峰，等.基于前景理论的多目标灰靶决策方法[J].控制与决策，2013，28（3）：345-350.

[7] 王坚强，王君.基于区间灰色区间数的多准则决策方法[J].管理学报，2009，6（9）：1150-1153.

[8]JAHANSHAHLOOGR，LOTFIFHosseinzadeh，IZADIKHAH M.An algorithmic method to extend TOPSIS for decision making problems with interval data[J].Applied Mathematics and Computation，2006，175（2）：1375-1384.

[9] 潘巍，王阳生，杨宏戟.D-S证据理论决策规则分析[J].计算机工程与应用，2004，14：14-17.

[10]陈增明.群决策环境下证据理论决策方法研究与应用[D].合肥：合肥工业大学，2007.

[11]李黎，张烈平.基于灰色关联和D-S证据理论的感应电转子故障诊断[J].计算机测量与控制，2012（6）：1492-1494.

[12]孙全，叶秀清，顾伟康.一种新的基于证据理论的合成公式[J].电子学报，2000，28（8）：117-119.

[13]王育红，党耀国.基于灰色关联系数和D-S证据理论的区间数投资决策方法[J].系统工程理论与实践，2009，29（11）：128-134.

[14]李鹏，刘思峰.基于灰色关联分析和D-S证据理论的区间直觉模糊决策方法[J].自动化学报，2011（8）：993-998.

[15]李特，冯琦，张堃.基于熵权灰色关联和D-S证据理论的威胁评估[J].计算机应用研究，2013（2）：380-382.

[16]韦兰用，韦振中.区间数判断矩阵中区间数的运算[J].数学的实践与认识，2003，9：75-79.

[17]党耀国，刘思峰，刘斌.基于区间数的多指标灰靶决策模型的研究[J].中国工程科学，2005（8）：31-35.

[18]秦玉慧，罗党.基于优性指标的灰色风险型多指标决策方法[J].河南教育学院学报：自然科学版，2007，3：4-6.

[19]谢乃明，刘思峰.考虑概率分布的灰数排序方法[J].系统工程理论与实践，2009，4：169-175.

[20]郭秀英.区间数指标权重确定的熵值法改进[J].统计与决策，2012，17：32-34.

[21]罗毅，李昱龙.基于熵权法和灰色关联分析法的输电网规划方案综合决策[J].电网技术，2013，37（1）：77-81.

[22]BAE H R，GRANDHI R V，CANFIELD R A.Sensitivity analysis of structural response uncertainty propagation using evidence theory[J].Structural and Multidisciplinary Optimization，2006（4）：270-279.