基于区间数和变权理论的雷达网作战能力评估方法❋
钱小东 李照顺 柳 强
(1.海军指挥学院 南京 211800)(2.92138部队 常州 213137)
1 引言
现代海上编队雷达系统面临严重的综合电子干扰、反辐射导弹(ARM)、目标隐身技术和低空突防的威胁,相应对海上编队雷达网的对空警戒防御能力提出了更高的要求。由于不同的舰艇装备有不同雷达,为使海上编队雷达网在作战中拥有较高的作战能力,在静态条件下必须对各种不同编队方式的雷达网作战能力进行评估,选择出拥有较优雷达网作战能力的编队方式。
考虑到编队雷达网作战能力评估的复杂性和不确定性,其各项作战能力指标大多是定性指标,不能用固定值表示,只能用区间数表征。而且目前作战能力评估中常用的常权综合算法,权重值通常都是固定的,受评估人员的主观因素影响比较重,导致评估的最终结果无法反映真实情况。因此,本文提出了基于区间数和变权理论的编队雷达网作战能力评估方法,提高了辅助决策的可靠度。
2 常权综合算法中存在的问题
2.1 编队雷达网“四抗”作战能力评估指标体系
通过对海上编队雷达网“四抗”能力的定性分析,运用层次分析法得出对其“四抗”作战能力进行综合评估的层次结构模型[1~2],如图1所示。指标体系共分为三层,第一层是目标层,即海上编队雷达网“四抗”作战能力;第二层和第三层是指标层,其中第二层指标是“四抗”的四个方面能力,第三层是“四抗”的因素层,包括“四抗”能力的各个主要因素。

图1 海上编队雷达网作战能力评估指标体系
2.2 常权综合
采用最常用的常权综合算法——层次分析法(AHP)[1],对海上编队雷达网“四抗”作战能力进行评估。假定有三种不同编队方式,指标体系中各指标取值[2~3]如表1所示。
根据层次分析法,求得第二层指标B1~B4的权重值为u1=[0.7186,0.1554,0.0630,0.0630],第三层指标c1~c4的权重值为u2=[0.7073,0.0438,0.0584,0.1904],c6~c8的权重值为u3=[0.3333,0.3333,0.3333]。然后通过加权求和分别求得编队方式1的抗干扰能力为B1=0.8089,抗ARM能力为B2=1,抗隐身能力为B3=1.5554,抗低空能力为B4=0.6,最后求得编队雷达网“四抗”作战能力为A1=0.8726。同理,编队方式2的B1=0.8089,B2=1,B3=1.5554,B4=0.56,A2=0.8700。编队方式3的B1=0.8795,B2=1,B3=1.1110,B1=0.3333,A3=0.8784。

表1 三种编队方式的各指标值
结果表明,编队方式3的雷达网“四抗”作战能力比方式1、2高,所以选择编队方式3。但从表1可以直观看出,相比编队方式3,方式1、2雷达网内的单部雷达抗干扰能力相近,但频域覆盖范围更广,频率重叠系数更小,极化类型数更多,且配有米波雷达,所以按常理编队方式1、2的雷达网抗干扰能力比方式3更高,且由于其抗隐身能力和抗低空能力也相比编队方式3高很多,所以整体“四抗”作战能力应该都比方式3更高。
造成该现象的原因有:1)c1、c4、c5、c6、c9这些评估指标的指标值在一个区间内变化,人为确定成一个固定值对评估结果的准确性造成了一定的影响。例如,“频率重叠系数c4”的指标值其实是一个区间数,人为地参照“频率重叠系数评价指标得分表[2]”将其确定成一个固定值,影响了评估结果;2)评估指标权重值的确定受主观因素影响严重,某些因素的权重值较大,某些因素的权重值较小,导致在雷达网作战能力评估中相应因素的作用被放得过大或者过小,评估结果最终无法反映真实情况。例如,从上文可以看出,三种编队方式的抗干扰能力B1相差不大,而指标B1通过层次分析法得到的权重值较大,为0.7186,导致编队方式3相对编队方式1、2在指标B1上的一点优势反映在最终评估结果上时被放得过大,评估结果不符合实际。
针对上述两个问题,1)采用区间数描述指标值,以期克服给指标取固定值对评估结果造成的不利影响;2)为改变评估指标的权重完全由人确定,受主观因素影响较大的问题,吸取变权理论评估指标的权重依据评估指标取值来确定的方法,使评估更加客观。因此,本文提出将区间数与变权理论相结合的方法,研究海上编队雷达网作战能力的评估问题。
3 理论方法描述及实施步骤
3.1 区间数理论
定义1 若∀aL,aH∈R且aL<aH,称闭区间[aL,aH]为实数域R 上的区间数,[R]表示R 上的全体闭区间数的集合;∀a∈R,点a可记为区间数[a,a];若0<aL≤aH,称[aL,aH]为实数域R 上的正闭区间数[4];
定理1 [aL,aH]和[bL,bH]为两个区间数,区间数运算规则如下[5~6]:
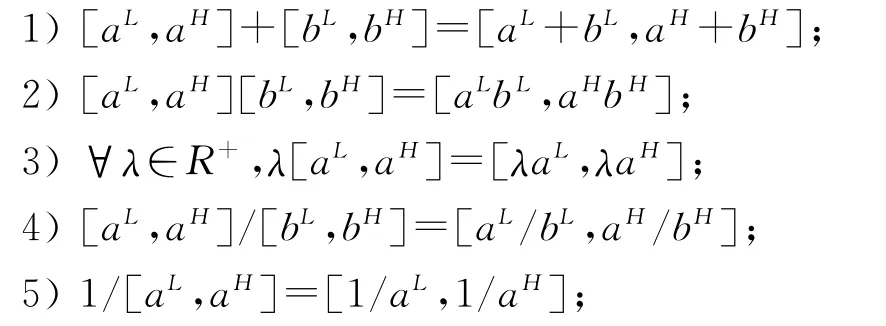
定义2 对[aL,aH]∈R,定义在区间[0,1]上的映射Fα(a):
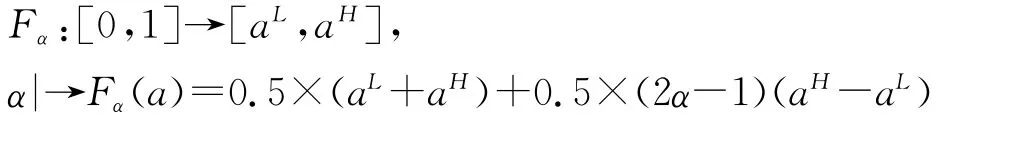
α为评估人员对[aL,aH]的心态指标[4],即在实际的决策问题中,由于评估人员自身条件和所面临的外部环境的不同,会有乐观,悲观以及中立三种心态。一般来说,评估人员的心态不同会导致不同的决策结果。
定义3 区间数排序规则:∀[aL,aH]和[bL,bH]∈R
1)若∀α∈[0,1]均有Fa(α)≤Fb(α),则称[aL,aH]≤[bL,bH];
2)若∀α∈[0,1]均有Fa(α)=Fb(α),则称[aL,aH]=[bL,bH];
以评估人员的心态指标α=0.5为基准,此时Fα(0.5)=0.5(aH+aL)。当心态指标α>0.5时,Fa(α)=aaH+(1-α)aL>Fα(0.5),即编队“四抗”作战能力相对α=0.5时增大,所以说此时的评论人员对所评价编队“四抗”作战能力主观上充分肯定;反之,当心态指标α<0.5时,Fa(α)=aaH+(1-α)aL<Fα(0.5),即编队雷达网“四抗”作战能力相对α=0.5时减小,此时的评估者对所评价编队“四抗”作战能力主观上持质疑态度。从以上定义中可以看出,通过在区间数中加入心态指标α,可以做到对编队“四抗”作战能力评估进行排序时充分体现评估人员的主观能动性。
3.2 基于变权理论的指标权重确定方法
本文借鉴汪培庄教授提出的变权思想[7],建立了基于熵值变化的指标属性权重计算方法。计算步骤如下:
1)设N={m1,m2,…,mn}为待评估舰艇编队方式集合,C={c1,c2,…,cn}为“四抗”作战能力评估指标集合,按照上节的区间数理论,构造“四抗”作战能力评估的区间数决策矩阵Z=(zij)n×m,其中zij表示第i种编队方式的第j个指标属性值。
2)图1中第三层的九个评估指标中,频率重叠系数c4、系统隐蔽性c5是成本型指标,即这些指标的值越大,雷达网作战能力越小,其余的指标都是效益型指标,即这些指标的值越大,雷达网作战能力越大。将区间数决策矩阵Z=(zij)n×m规范化,消除量纲的影响。规范化的决策矩阵为R=(rij)n×m,rij为区间数[rLij,rHij],其中[8~9]:

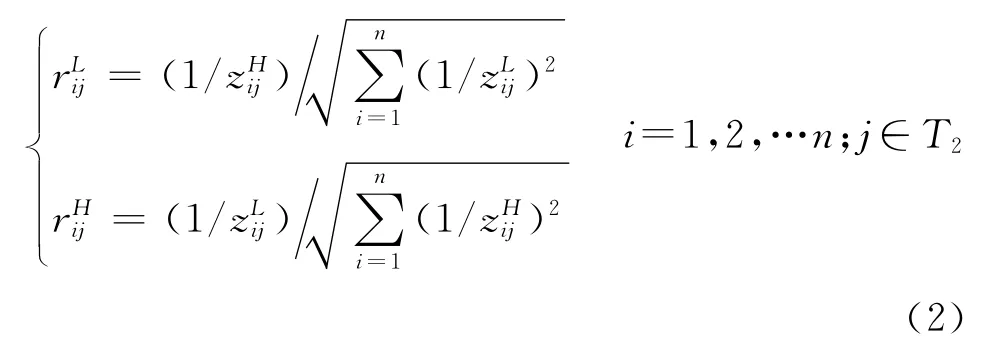
其中T1、T2分别为效益型指标和成本性指标。
3)按照信息论知识,求信息熵,则第j个属性的信息熵为
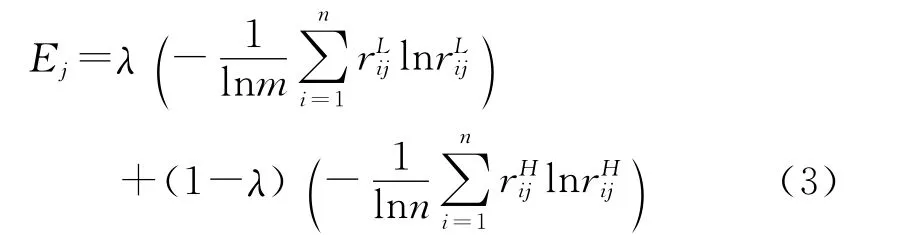
其中λ∈(0,1),与心态指标α类似,是评估人员对区间数的平衡系数,体现评估人员的主观心理影响。
4)求解指标的差异度Dj=1-Ej,定义第j个评估指标的权重为[10]

3.3 雷达网作战能力评估实施步骤
利用区间数表示雷达网作战能力指标取值范围,建立作战能力评估指标区间数决策矩阵,求取作战能力属性熵值,计算各指标权重,将规范化决策矩阵与权重综合得到总的作战能力值。基于区间数和变权理论的雷达网作战能力评估算法实施步骤如下:
1)构造编队雷达网作战能力指标区间数决策矩阵 Z= (zij)n×m,把 Z 规 范 化 得 到 矩 阵R =(rij)n×m,把R 归一化得到矩阵V=(vij)n×m;
2)利用归一化后的矩阵V=(vij)n×m计算信息熵Ej,输入修正系数λ,计算得到各指标权重wj;
4)输入心态指标α,根据定义2计算F(α);
5)根据定义3对区间数向量P进行排序,确定作战能力较优的编队方式。
3.4 实例计算
对3.2节中提到的三种编队方式,用区间数表示各指标的实际取值,如表2所示。

输入评估人员对区间数的修正系数λ=0.5,然后将R归一化,计算得到各指标的权重W=[0.1087,0.1130,0.1106,…,0.1130,0.1087,0.1096],最后求得雷达网作战能力综合指标区间数向量P=([0.4406,2.1550],[0.4394,2.1550],[0.3654,1.9116])。

表2 三种编队方式各指标的实际值区间数
对于中立的评估人员,输入心态指标α=0.5,计算得到各指标的映射值为F=(1.2978,1.2972,1.1385),对区间数向量P按大小进行排序,最终得到编队雷达网作战能力的排序:编队方式1>编队方式2>编队方式3。
针对消极、中立以及乐观的评估者,得到以下排序结果,如表3所示。

表3 评估结果表
从表3可以看出,基于区间数和变权理论的静态条件下海上编队雷达网作战能力评估方法,无论评估者心态如何,加入修正系数以后,海上编队“四抗”作战能力的排序基本不会发生变化,只有当所评价的两组编队方式的雷达网作战能力相近时,评估者的主观因素才会影响评估结果。所以这种方法体现了海上编队雷达网作战能力的实际情况,使评估结果尽量少的受到评估人员主观因素的影响。
4 结语
在对海上编队雷达网作战能力的评估中,由于其大多数指标都不是一个固定值,而是在一定范围内变化的区间数,因此本文利用区间数理论描述各评估指标,并对作战能力评估结果进行了排序,使得评估结果更加贴合实际。在计算指标权重时,借用计算信息熵的方法,使得权重值随样本空间实际指标值变化,避免了常权综合方法由于权值的固定不变造成某些情况下的评估结果不合理的情况。在类似的作战能力评估中,该方法也具有一定的参考价值。
[1]方良.海上编队雷达组网优化问题研究[D].南京:海军指挥学院,2008.
[2]陈军,冯卫强,赵虎强.防空组网雷达“四抗”能力综合评估[J].指挥控制与仿真,2009,31(2):62-64.
[3]陈永光,李修和,沈阳.组网雷达作战能力分析与评估[M].北京:国防工业出版社,2006:168-173.
[4]冯卉,邢清华,宋乃华.一种基于区间数的空中目标威胁评估技术[J].系统工程与电子技术,2006,28(8):1201-1203.
[5]覃菊莹.区间数判断矩阵的一致性及权重计算[J].数学的实践与认识,2010,40(8):165-171.
[6]韩朝超,黄树彩,王凤朝.基于区间数熵权分析的空中目标威胁评估方法[J].战术导弹技术,2010(1):32-35.
[7]汪培庄.模糊集与随机集落影[M].北京:北京师范大学出版社,1985:56-59.
[8]王小艺,刘载文,侯朝桢,等.基于模糊多属性决策的目标威胁估计方法[J].控制与决策,2007,22(2):215-219.
[9]Tran L,Duckstein L.Comparison of fuzzy numbers using a fuzzy distance measure[J].Fuzzy sets and systems,2002,130:331-341.
[10]王毅,赵建军,付文龙,等.基于区间数熵的TOPSIS防空作战威胁评估方法[J].弹箭与制导学报,2003,32(12):114-116.

