基于STFT与WVD的LPI雷达信号检测❋
肖 鹏 杨承志 吴宏超 吕亚昆 李健伟
(空军航空大学 长春 130022)
1 引言
LPI(Low Probability of Intercept)雷达在我周边国家和地区迅猛发展,很快占据战场传感器的主体地位,因此对LPI雷达信号的检测将直接影响到武器装备性能的发挥。为此众学者研究总结出了[1]能量检测法、小波变换法、时频分析法、循环平稳分析、高阶累积量等。能量检测算法是在加性独立高斯白噪声背景下的较好检测法,但其检测能力对噪声平稳性依赖较强。WVD(Wigner-Ville Distribution)虽具有较好的时频聚集性和时频分辨率,但当处理多分量信号时存在严重的交叉项。小波变换虽不存在交叉项的困扰,但其时频分辨力远远不及WVD,并且针对不同的信号需要选用不同的小波基。文献[2]利用信号的循环平稳特性进行信号的盲检测和估计,论证了在未知噪声、强干扰的情况下,只要信号和噪声采用不同的循环频率,才有优良的检测性能,算法计算量大,需要的观测时间长。文献[3]将时频图像和神经网络技术应用于LPI雷达信号检测,达到了较好的效果,但算法过于复杂,难以满足战场实时性的需求。
为此本文提出了基于STFT(short-time Fou-rier transformation)与WVD联合的LPI雷达信号检测算法,该算法既抑制了 WVD交叉项的干扰,又保留了WVD优良的时频聚集性和时频分辨力。
2 WVD分布简介
设信号x(t),y(t)是连续的时间信号,其傅里叶变换分别是 X(ω),Y(ω),则x(t),y(t)的联合WVD分布定义为

连续的一维WVD定义为

式中:t为时间变量;“*”表示复共轭。
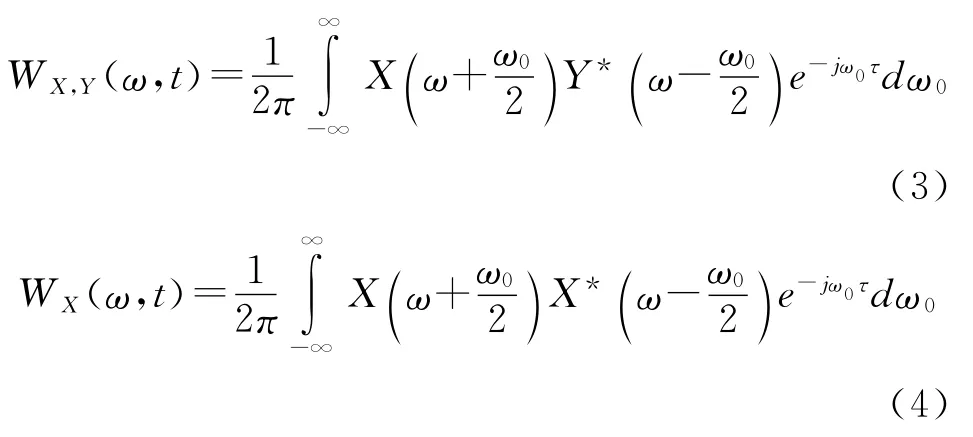
并且:

WVD是一个以时间和频率为自变量的描述信号幅度的三维函数[4],对于两个分量的信号z(t)=z1(t)+z2(t),其 中:z1(t)=Aej(φ1+2πf1t+πk1t2),z2(t)=Bej(φ2+2πf2t+πk2t2),其 WVD 为


由式(7)可以简化表示为

其中:WVDz1z2、WVDz2z1为交叉项,WVD的交叉项是无法避免的,并且当信号项变多时,交叉项会变得更加严重,以至于无法区分信号和交叉项。为此出现了抑制交叉项的诸多方法:如:伪 Winger-Ville分 布 (PWVD)、平 滑 Winger-Ville 分 布(SWVD)、平滑伪 Winger-Ville分布(SPWVD)等,这些变换都是从核函数的角度出发来减少交叉项的干扰,但同时也失去了WVD的分辨率优势。为了达到双赢的目的,学者又提出了诸多联合算法来使WVD得到更出色的表现:文献[5]提出了一种结合经验模态分解的WVD交叉项抑制新方法。将输入的多分量信号分解为单分量信号,利用WVD对单分量信号无交叉项的优势来保证WVD优良的性能,但是该方法计算量大,效果不够理想。
3 STFT变换简介
短时傅立叶变换基本思想是在每个特定时刻对信号s(t)加滑动的时间窗,并对窗内信号做局部傅立叶变换,得到信号的时变频谱[6],随着时间窗的移动,可以得到信号的STFT。
设待分析的时间连续信号为s(t),窗函数为h(t),h(t)是沿时间轴滑动的很窄的窗函数,s(t)信号的STFT变换定义如下:

式中,“*”代表复数共轭。
信号s(t)与窗函数相乘可以有效地抑制分析时刻以外的信号干扰,所以STFT是信号s(t)在时刻t的邻域内的局部频谱。当窗函数足够宽(h(t)=1)时,该STFT退变为经典傅里叶变换。为了更好的工程化运用,需要对STFT进行离散化处理:

式中h(n)为加窗函数。考虑一种极限情况:当h(n)足够窄,可以视为一个单位脉冲响应h′(n)=h(n),则可以采用单位采样序列的移位加权和表示。
离散短时傅里叶变换STFT可以在等频率间隔取样点ωr=2πr/N(r=0,1,2,…,N-1)上用FFT算法进行计算[7]。令STFTs(n,ωr)=STFTs(n,r),可得:

令m=l+n,l=k+qN,k=0,1,2,…,N-1,则式(11)可变为

式中:
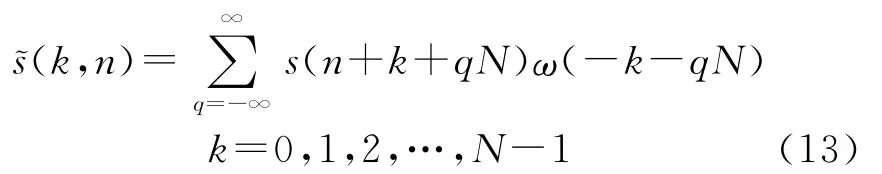
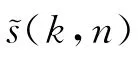
4 WVD和STFT算法的结合
从Winger-Ville分布和短时傅立叶变换的优缺点出发[8~9],可以寻求一种既可以满足优良时频分辨率又能避免交叉项干扰的新方法来对LPI雷达信号进行分析。为此,笔者从LPI雷达信号的波形特点出发,以解决抑制交叉项的核心问题为主要切入点,提出了WVD-STFT联合改进算法。
新算法首先对信号进行WVD和STFT变换,得到Ws(t,f)和STFTs(t,f),然后对二者进行点乘运算,当二者都有信号项时可以得到乘积结果,当Ws(t,f)的交叉项对应的STFTs(t,f)区域没有信号时,乘积自然为零,这时再经过带通滤波器就可以得到原始输入信号。通过这种结合便得到了易于工程化实现的LPI雷达信号检测方法,用公式可以表示为

其中,CS(t,f)为结合后的结果,“.*”代表矩阵的点乘。
5 仿真分析
LPI雷达是采用先进的搜索方式[10]、波形设计、功率管理等手段防止非合作截获接收机截获和检测其发射信号的先进雷达[11]。调频连续波(frequency modulation continuous wave,FMCW)信号由于具有良好的距离和速度分辨力,且易于工程化实现,所以首先被应用于现役装备中。为此笔者以最具代表性的FMCW信号为输入,检验新算法能否完成对LPI雷达的检测。
设置两个FMCW信号为:载频f10=2MHz,f20=1.5MHz;调制时间tm10=30ms,tm20=20ms;带宽B10=1MHz,B20=2MHz;信噪比SNR=0dB。
该双输入信号经过WVD和STFT变换得到的时频图如图1和图2所示。

图1 双输入LFMCW信号的WVD(SNB=0dB)

图2 双输入LFMCW信号的STFT(SNB=0dB)
从图中可以清晰看出:WVD具有优良的时频分辨率,然而交叉项的存在使得对原信号的检测变得十分困难;STFT变换虽不含交叉项的干扰,但频率分辨率较差。利用本文提出的新算法得到的时频分布如图3所示。

图3 WVD-STFT联合算法处理后的时频图(SNB=0dB)
经过新算法的处理可以较好地抑制交叉项的干扰同时兼具良好的时频分辨率,由此可为后续信号的参数估计和识别等奠定基础。
当信号其它参数不变,信噪比为SNR=-3dB时,该算法处理能力如图4所示。

图4 WVD-STFT联合算法处理后的时频图(SNB=-3dB)
当信噪比为-3dB时,算法仍能从背景噪声中提取出LPI雷达信号,虽有一些杂波干扰但是对后续信号处理不会产生影响,由此说明了算法的可行性。
6 结语
笔者从WVD和STFT变换的优缺点出发,提出了改进的 WVD-STFT联合算法。该算法在结合的过程中充分利用内积和滤波器的优势,既保留了应有的时频分辨率和时频聚集性又抑制了交叉项的干扰,是行之有效的LPI雷达信号检测算法。但是该算法在强背景噪声环境下处理能力有限,针对PSK或FSK信号检测效果不佳,还需在后续的研究中不断完善,以适应实际作战的需要。
[1]沈伟,冯志红,赵拥军.基于高阶累积量的LPI雷达信号检测[J].电子信息对抗技术,2012,27(2):1-5.
[2]ANTONIO F.Analysis of Low Probability of Intercept(LPI)Radar Signals Using Cyclostationary Processing[D].California:Naval Postgraduate School Monterey,2002.
[3]熊坤来,罗景青,吴世龙.基于时频图像和神经网络的LPI雷达信号调制识别[J].弹箭与制导学报,2011,31(5):230-233.
[4]苏峰,平殿发,简涛.基于 WVD和Hough变换二值积累的信号检测方法[J].舰船电子工程,2009,29(11):165-167.
[5]李振兴.基于经验模态分解的Winger-Ville分布交叉项抑制方法[J].航空兵器,2010(6):59-62.
[6]金朝娣,能昌信,王振翀,等.基于STFT的钻柱振动信号分析与应用[J].煤矿开采,2011,16(2):29-32.
[7]迟华山,王红星,郭奇,等.短时傅里叶变换在线性调频信号时频滤波中的应用[J].电讯技术,2012,52(2):155-159.
[8]张鑫,赵拥军.基于短时傅里叶变换和 Wigner-Ville分布的联合变换[J].电子对抗,2008(120):39-42.
[9]袁伟明,王敏,吴顺君,等.一种新的LPI信号的截获方法[J].电波科学学报,2005,20(1):73-76.
[10]仇金娇,冯西安,苏建军.基于小波分析的低截获信号检测方法研究[J].理论与方法,2013,32(2):20-22.
[11]张昕然,谢红.一种低信噪比下基于时频原子的复杂调制雷达信号分选方法[J].应用科技,2013,40(3):1-7.

