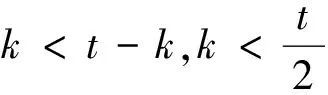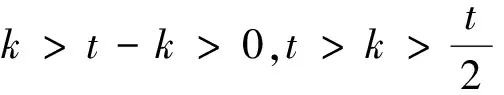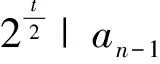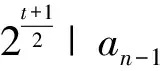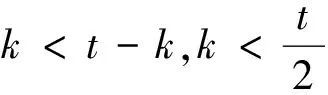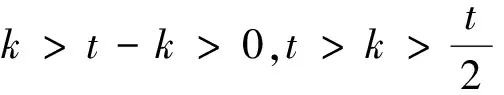整系数多项式有理根存在性的新判别法

赵元翔

(扬州职业大学 师范学院，江苏 扬州 225009)



整系数多项式有理根存在性的新判别法

赵元翔

(扬州职业大学 师范学院，江苏 扬州 225009)

给出了一种与艾森斯坦判别法截然不同的判断整系数多项式无有理根的方法，这种判别法不仅能够解决一类不能由艾森斯坦判别法直接判别的整系数多项式，而且对于复杂的整系数多项式能够做出迅速判断，对判断整系数多项式有理根的存在性有重要意义。

整系数多项式; 艾森斯坦判别法; 无有理根

在唐忠明、戴桂生教授主编、南京大学出版社出版的《高等代数》第73页上有这样一道题目[1]: 设f(x)是整系数多项式，且f(0)，f(1)都是奇数，证明f(x)没有有理根.如果f(x)=2x+1，则f(0)=1,f(1)=3均是奇数，而f(x)仍存在有理根。因此，该题是错误的命题，通过进一步探究,我们得到了一个较为完整的判断整系数多项式无有理根的方法如下：

定理1 设f(x)=anxn+an-1xn-1+…+a0是整系数多项式(n≥2)，且满足：

①首项系数an为奇数;

②f(0)为奇数;

③f(1)为奇数;

则f(x)无有理根.

则有f(x)=(sx-r)h(x),h(x)=bn-1xn-1+bn-2xn-2+…+b0.

因为f(0)=-rb0为奇数，所以r为奇数.

f(1)=(s-r)h(1)为奇数，故s-r为奇数，s为偶数.

由于f(x)的首项系数an=sbn-1，故首项系数为偶数，与已知矛盾，定理1得证.

例1 设p(≠2)是质数，证明f(x)=xp+xp-1+…+x+1无有理根.

(这是一条典型的通过变形利用艾森斯坦判别法判断的习题，用定理1证明如下.)

证明：根据首项系数为1，f(0)=1,f(1)=p均为奇数, 故f(x)无有理根.

将定理1做适当推广得：

定理2 若f(x)是整系数多项式，首项系数为奇数，对任意一奇一偶的整数a1,a2，有f(a1),f(a2)均为奇数，则f(x)无有理根.

设f(x)=(sx-r)h(x),h(x)=bn-1xn-1+bn-2xn-2+…+b0是整系数多项式,

a2为偶数，f(a2)=(sa2-r)(bn-1a2n-1+bn-2a2n-2+…+b1a2+b0).

因为sa2,bn-1a2n-1,bn-2a2n-2,…,b1a2都是奇数，f(a2)也是奇数, 所以r,b0都是奇数.

a1为奇数，f(a1)=(sa1-r)(bn-1a1n-1+bn-2a1n-2+…+b1a1+b0).

因为f(a1)是奇数, 所以sa1-r是奇数, 又因为a1,r是奇数, 所以s必为偶数, 因此f(x)的首项系数sbn-1是偶数(矛盾), 故f(x)无有理根，证毕.

例2 试证明f(x)=(x-2013)2012(x-2012)2013+1001无有理根.

证： 因为f(2013)=f(2012)=1001为奇数，首项系数是1, 所以由定理2得f(x)无有理根.

观察上面的定理1和定理2，均要求首项系数为奇数，然而首项系数是偶数时，何时成立？

定理3 设f(x)=anxn+an-1xn-1+…+a0是整系数多项式(n≥2)，且满足：

①2|an，4⫮an;

②f(0)，f(1)是奇数

③2|an-1;则f(x)无有理根.(条件①可以改为(an,2m)=2,其中m是无穷大的正整数).

设f(x)=(sx-r)h(x),h(x)=bn-1xn-1+bn-2xn-2+…+b0是整系数多项式,

则f(x)=sbn-1xn-1+(sbb-2-rbn-1)xn-2+…+(-rb0)=anxn+an-1xn-1+…+a0.

f(0)是奇数，则r,b0是奇数.

f(1)是奇数，则s-r是奇数，s是偶数, 因为2|an,4⫮an，an=sbn-1，所以bn-1是奇数，则an-1=sbn-2-rbn-1是奇数，与条件③矛盾，故f(x)无有理根.

定理4.1 设f(x)=anxn+an-1xn-1+…+a0是整系数多项式(n≥3),

若 ①4|an，8⫮an;

②f(0)，f(1)是奇数;

③4|an-1且2|an-2.

则f(x)无有理根.

定理4.2 设f(x)=anxn+an-1xn-1+…+a0是整系数多项式(n≥3)，且满足：

①4|an，8⫮an;

②f(0)，f(1)是奇数;

③2|an-1，4⫮an-1且an-2是奇数.

则f(x)无有理根.

由于an=sbn-1，(an,2m)=4,因此可将f(x)分为三类讨论：

(1)2⫮s，4|bn-1(不成立，s必为时偶数),

(2)2|s，2|bn-1时,

i)bn-2为偶数⟺(an-1,2m)=2⟺an-2为偶数,

ii)bn-2为奇数⟺4|an-1⟺an-2为奇数.

(3)4|s，2⫮bn-1时, 此时an-1必为奇数.

假设“4|an-1且2|an-2”.

分类(2)中 i)要求(an-1,2m)=2以及分类(3)与4|an-1矛盾；

分类(2)中ii)要求an-2为奇数与2|an-2矛盾，故f(x)无有理根.

假设“2|an-1，4⫮an-1且2⫮an-2”即“(an-1,2m)=2且2⫮an-2” .

分类(1)中ii)和分类(2)(3)与(an-1,2m)=2可，分类(1)中 i)与2⫮an-2矛盾，故f(x)无有理根.定理4.1和定理4.2获证.

定理5 设f(x)=anxn+an-1xn-1+…+a0是整系数多项式(n≥3)，且满足：

①(an,2m)=2t(t≥0的偶数) ;

②f(0)，f(1)是奇数;

设s=2ks′,bn-1=2t-kbn-1′,(s′,2)=1,(bn-1′,2)=1,0

定理6 设f(x)=anxn+an-1xn-1+…+a0是整系数多项式(n≥3)，且满足：

①(an,2m)=2t(t≥1的奇数);

②f(0)，f(1)是奇数;

证：由于an-2是奇数，故由an-2=sbn-3-rbn-2可知bn-2是奇数.

设s=2ks′,bn-1=2t-kbn-1′,(s′,2)=1,(bn-1′,2)=1,0

在定理3到定理6这4个定理中，条件②“f(0)，f(1)是奇数” 换为“a,b为一奇一偶整数，f(a)，f(b)是奇数”，结论仍然成立(证明略).

例3 证明整系数多项式f(x)=2048x7+1993x5+9x+15无有理根.

证： 首项系数an=2048=211，选用定理6证明.

由于f(0)=15是奇数

f(1)=2048+1993+9+15=4065是奇数，an-1=0.26|0且an-2=9为奇数, 根据定理6得f(x)无有理根．

[1] 唐忠明, 戴桂生.高等代数[M].南京大学出版社, 2000.

[2] 北京大学数学系几何与代数教研室前代数小组.高等代数[M].高等教育出版社(第三版), 2003.

(李鑫)

A new criterion for judging the existence of rational roots of an integer polynomial

ZHAO Yuan-Xiang

(Yangzhou Polytechnic College，Yangzhou 225009, Jiangsu China)

A new criterion is given for recognizing whether or not an integer polynomial has rational roots. This criterion is not only absolutely different from Eisenstein Criterion, which cannot directly present judgment for some integer polynomials, but can also quickly produce decision for complex integer polynomials. Therefore, this new criterion possesses significance in judging the existence of rational roots of an integer polynomial.

integer polynomial; Eisenstein Criterion; no rational root

O151

A

1003-8078(2014)03-0016-03

2013-10-17 doi 10.3969/j.issn.1003-8078.2014.03.05

赵元翔，男，江苏扬州人，扬州职业大学师范学院学生，研究方向为基础数学。