复杂导线垂直断面地势下直流线路无线电干扰计算的信赖域正则化遗传算法
邓 军 郝艳捧 李立浧 肖 遥
(1.华南理工大学 广州 510640 2.南方电网超高压输电公司检修试验中心 广州 510663)
1 引言
高压或特高压直流输电技术广泛用于西电东送输电工程,然而随着电压等级的提高,其电磁环境影响越来越受到公众的关注和线路设计的重点考虑[1]。无线电干扰水平是直流输电线路环评的重要电磁环境指标之一,其主要危害是干扰输电线路周围的无线电广播、电视等无线电信号。利用激发函数法研究了特高压直流线路导线5 分裂的无线电干扰特性[2],考虑无线电干扰影响研究了洛扎渡—广东等特高压直流输电线路的导线选型问题[3,4],基于气体放电理论分析了正负直流绞线电晕起始电压[5,6],利用特高压基地试验线段开展了直流线路无线电干扰特性研究[7]。上述理论分析和特高压基地的实际测量均假设输电线路导线垂直断面为平面,结合场域边界条件,利用马克特-门格尔法、逐步镜像法进行无线电干扰分析和计算。然而实际的输电线路导线垂直断面经常处于不平坦地形。基于上述文献中的计算方法不能直接用于复杂导线垂直断面地势下直流线路无线电干扰计算。
目前,基于优化的模拟电荷法开展了复杂地形情况下高压交流输电线路电磁环境特性分析,但该方法是凭经验设置模拟电荷的位置[8,9]。然而,利用遗传算法分别进行电场逆运算的输电导线弧垂和特高压绝缘子均压环优化,提高了计算结果精度[10,11]。因此,基于上述遗传算法优化复杂导线垂直断面地势下直流线路的模拟电荷位置,进而开展计算无线电干扰分布。
基于遗传算法和信赖域正则化法分别优化计算直流输电线路模拟电荷空间位置和电荷量,结合直流线路无线电干扰计算的国际无线电干扰特别委员会(CISPR)方法,开展复杂导线垂直断面地势下直流线路无线电干扰计算的信赖域正则化遗传算法研究。并将该方法与Levenberg-Marquardt 法、阻尼高斯-牛顿法进行算法收敛性和稳定性的比较分析,并分析了云广特高压直流线路3个断面的无线电干扰理论计算值与测量值的误差,验证该方法的计算精度。
2 复杂导线垂直断面地势下直流线路无线电干扰分布计算方法
2.1 物理模型假设
本方法适用的直流线路导线模型有:
(1)双极导线电压已知,电荷分布沿线路无畸变。
(2)双极导线具有相同半径、彼此间相互平行的无限长光滑圆柱形导体。线路档内沿线路方向的地势较平坦,而导线垂直断面呈起伏地势。从而将直流输电线路简化为导线垂直断面的二维场问题。
(3)大地为无穷大良导体,其电位为零。
2.2 复杂导线垂直断面地势下直流线路导线表面最大梯度计算方法
基于上述直流输电线路的模型假设,结合模拟电荷法处理开域电场问题的优势,建立了复杂导线垂直断面地势下直流输电线路导线表面最大梯度计算模型如图1 所示。然而传统方法只针对平坦的导线断面,利用镜像电荷等效大地表面的感应电荷,计算较为简便。但对于输电线路导线断面具有起伏地势的情况,无法直接设置导线镜像电荷。
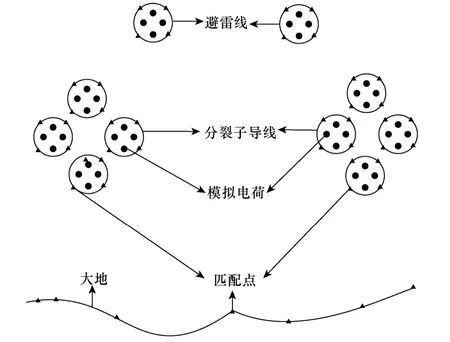
图1 复杂导线垂直断面地势下直流双极模型Fig.1 The complex vertical section terrains of DC bipolar conductor model
利用模拟电荷法计算复杂导线垂直断面地势下直流输电线路导线表面最大梯度需要解决的问题有:①双极导线和地线内模拟电荷的位置和电荷量;②双极导线和地线镜像电荷的位置和电荷量。因此基于最小二乘法原理建立所有模拟电荷在匹配点产生的电位满足式(1)的优化目标f。
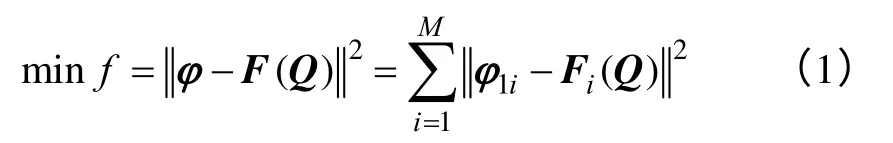
式中,M为导线表面的匹配点数量;F为非线性算子;Q、φ 分别为未知模拟电荷的电量向量和已知的匹配点的电位向量;φ1i为导线、避雷线或大地表面第i个匹配点的电位。
为实现对非线性算子F(Q)的近似,利用泰勒公式将 F(Q+δQ)在Q 处的泰勒展开。当足够小时,采用一次近似且忽略其余的高阶小量,得到
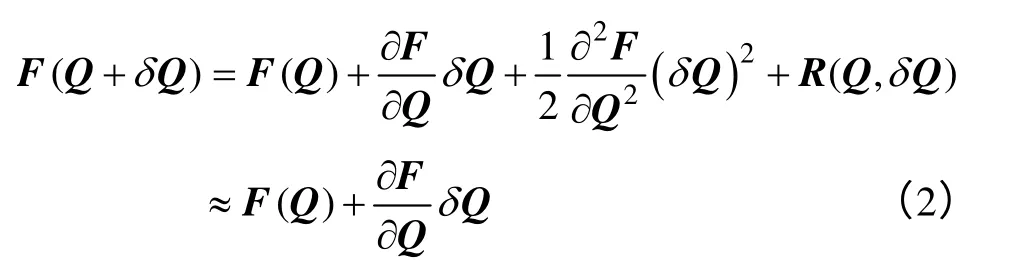
设 Q*=Q+δQ是方程φ-F(Q)的准确解,则在接近于Q*的Q 处可由式(2)得到如下线性算子方程。
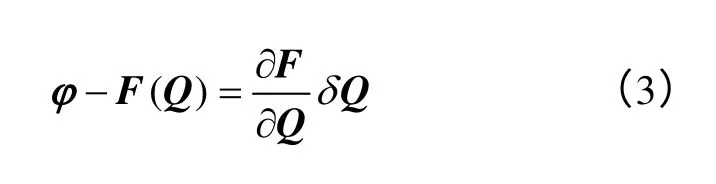
采用高斯-牛顿法等线性化式(3)会遗传原非线性方程的病态特性,故需引入正则化技术。然而传统的Levenberg-Marquardt 法是将正则化施加在δQ 上的爬行法,该方法存在的问题有:①因正则化施加在δQ 而非Q 导致无法针对求解的特征进行控制;②准确解Q*依赖初始解Q0和最小化路径δQk;③采用不同方法求解δQk得到的准确解Q*不同;④δQ 较大时可能导致目标函数值的增加。因此为克服和改善爬行法的问题,采用正则化施加在Q 上的全局正则化方法。同时根据具有全局收敛性的信赖域法策略不仅限制步长且获得新的下降方向。设非线性问题式(1)和线性化后的方程在大小为η 的区域内等效,同时结合线性化处理的式(3),基于全局正则化且通过优化问题在该区域内搜索一个最佳的δQ 如式(4)。
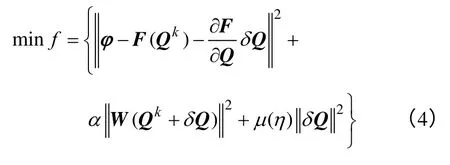
式中,W为线性算子;η为信赖域大小;μ(η)为罚函数;α为正则化参数;Qk为当前迭代解。
对于式(4)所示的优化问题,利用f为极小解的必要条件是f 的梯度为零的点,得到式(5)的线性方程。
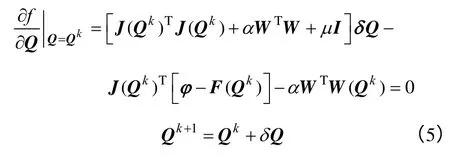
式中,JT(Qk)为雅可比矩阵的转置 JT(Qk)=;I为单位矩阵;Qk+1为第k+1 步迭代解。
式(1)的非线性最小二乘问题的求解归结为其法方程的求解如式(5)。同时基于求解式(5)的δQ通过式(6)的信赖域方法确定适合的δQ。

式中,Δf为非线性目标值的改变;Δf1为线性化目标值的改变;τ为信赖域控制参数;fk+1、fk分别为k+1 和k次迭代非线性目标值;为k+1次迭代线性化目标值,其定义如
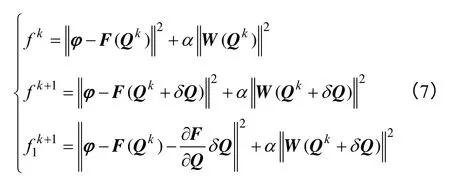
由式(5)~式(7)确定的直流输电线路双极导线、避雷线和大地镜像电荷的电荷量,直流双极分裂导线表面任意一点的电场强度可根据叠加原理计算,双极分裂导线的表面电场强度计算如式(8)。
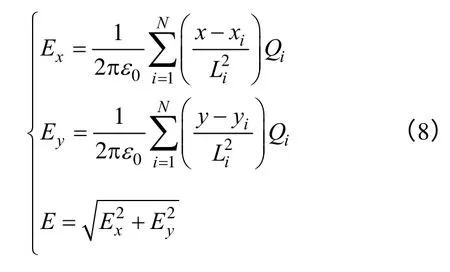
式中,E为电场强度的大小,其分量分别为Ex和Ey;2iL为模拟电荷至计算点的距离;N为模拟电荷的总数;(x ,y ),(xi,yi)分别为计算点和第i个模拟电荷的空间坐标;ε0为空气的介电常数。因此,基于式(8)计算直流双极导线表面各点场强,求解导线最大表面场强gmax。
基于直流输电线路导线表面电场式(8)计算最大电位梯度,结合导线半径和计算点与正极的距离等参数,直流线路无线电干扰计算的CISPR 方法如式(9)[12]。
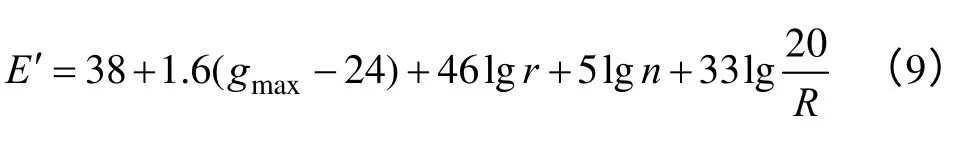
式中,E'为特高压直流无线电干扰值;r为子导线半径;n为分裂导线数;R为参考点至最近导线的空间距离。
2.3 基于遗传算法的模拟电荷空间位置优化
上述全局正则化方法是基于模拟电荷的位置已知。然而复杂导线垂直断面地势下直流线路电场受地面高低不平的影响,引起模拟电荷在导线、避雷线内及其相对大地的镜像电荷位置发生偏移。采用自适应遗传算法能够优化模拟电荷空间位置,该方法随个体适应值自动调整交叉和变异概率,克服传统遗传算法进化缓慢的问题。
根据模拟电荷法的原理,式(1)中的模拟电荷必须在非计算场域的导线、避雷线内,或位于大地表面以下。因此模拟电荷的位置满足式(10)的约束条件。
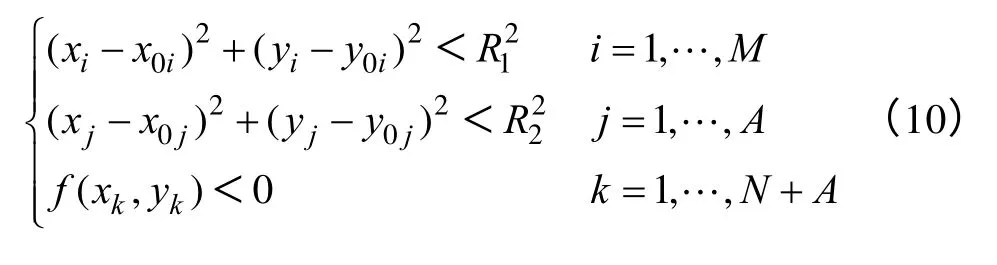
式中,(xi,yi)、(xj,yj)分别为分裂子导线和避雷线内的模拟电荷坐标;(xk,yk)为大地表面以下的镜像模拟电荷坐标;R1、R2分别为分裂子导线和避雷线的半径;A、N 分别为避雷线内模拟电荷的数量和总模拟电荷数量;f(xk,yk)为描述大地表面曲线的函数。
自适应遗传算法优化模拟电荷空间位置的步骤如下[13]:
(1)模拟电荷空间位置编码。根据式(10)的模拟电荷空间位置取值范围,将导线和避雷线的模拟电荷坐标与其所在子导线的中心做差值,得到导线和避雷线模拟电荷取值范围为对应的直径。为提高分辨率将导线和避雷线采用6 位二进制编码,镜像电荷采用10 位二进制编码。
(2)初始种群的产生。导线和避雷线的模拟电荷分别均分布于直径1/4 的圆环,各镜像电荷分别位于相对垂直地面的等距离镜像位置。
(3)适应度的确定。遗传算法优化模拟电荷空间位置的目标是优化结果的模拟电荷在匹配点产生的电位误差满足预先的误差。因此将式(1)作为适应度函数评价个体的优劣。若则输出寻优结果,停止迭代;否则转入步骤(4)。其中fmax、fmin分别为当前种群中最优和最差个体的函数值,ε为给定精度。
(4)遗传规则的设计。主要包括选择、交叉和变异。其中选择规则是按适应度大小对个体进行排序,从中选取i个适应度最大个体,按照式(11)进行选择概率 Ps(xi)。
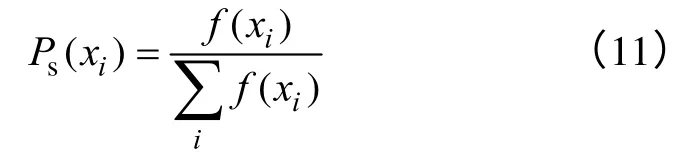
交叉规则采用两位交叉方式,自适应交叉概率PC为
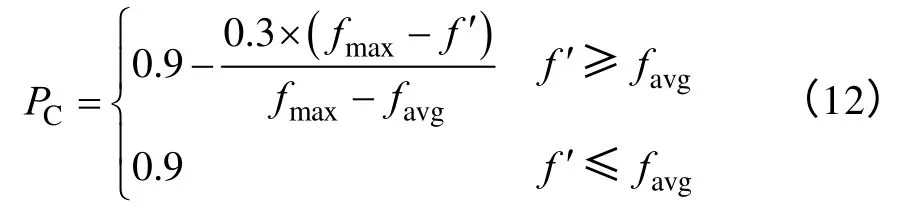
式中,favg为群体的平均适应度; f'为两交叉个体较大的适应值。
变异规则是将每个个体的每两位二进制编码随机产生一个在(0,1)之间的数,若大于个体的变异率,则该编码由1 变成0,或由0 变成1,否则该编码不变异。其变异概率Pm为
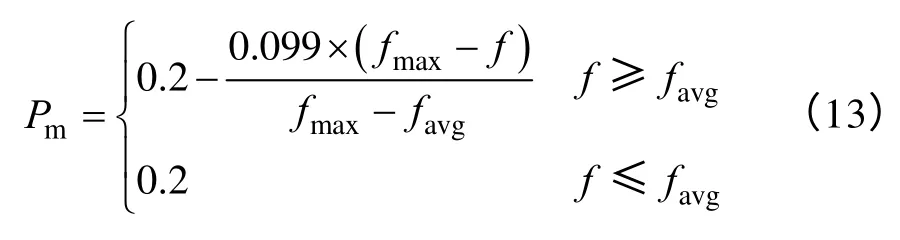
(5)保留较优个体。用子代种群一半数目的适应值较大的个体替代父代种群适应值较小的相同数目个体,提高获得最优个体的概率。将当前保留的新种群作为步骤(2)的初始种群重新计算。
通过遗传算法产生直流双极电场计算的模拟电荷空间位置,同时利用信赖域法的正则化方法优化模拟电荷的电量,达到优化复杂导线垂直断面地势下直流线路电场计算的模拟电荷位置和电荷量的双重目标,然后计算直流输电线路导线表面最大梯度,结合CISPR 无线电干扰方法进行计算。其主要计算流程如图2 所示。
3 复杂导线垂直断面地势下直流线路无线电干扰的算例分析
为验证理论计算方法的有效性,结合实际的云广特高压直流输电线路导线垂直断面的测试数据,基于Levenberg-Marquardt 法、阻尼高斯-牛顿法和信赖域正则化的遗传算法仿真计算复杂导线垂直断面地势下直流线路无线电干扰分布问题。并对比分析马克特-门格尔法和逐步镜像法的无线电干扰计算结果,验证了信赖域正则化遗传算法的可靠性。
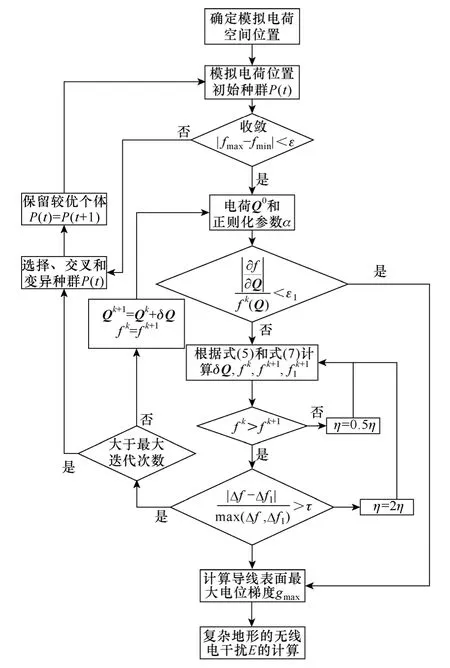
图2 复杂导线垂直断面地势下直流双极无线电干扰计算流程Fig.2 Flowchart of DC bipolar RI for the complex vertical section terrains
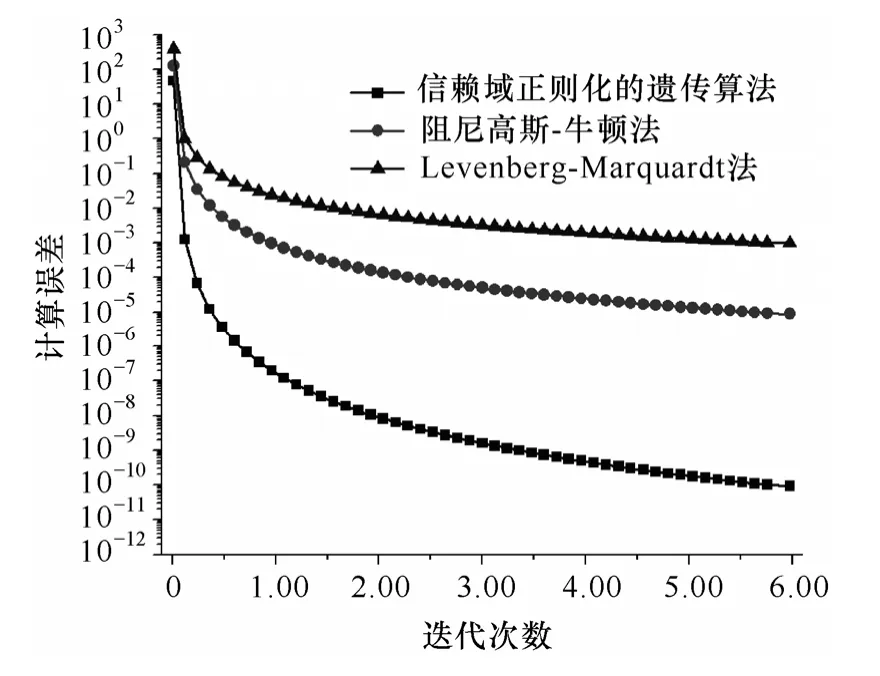
图3 信赖域正则化的遗传算法分析复杂导线垂直断面地势下直流线路无线电干扰的收敛性分析Fig.3 The convergence of trust region regularization genetic algorithm for DC bipolar RI of the complex vertical section terrains
计算误差与迭代次数间的变化关系分析如图3所示。因Levenberg-Marquardt 法是将正则化施加在δQ 而非Q,同时较大的δQ 将可能导致计算误差的增加,其计算误差的收敛速度明显小于将正则化施加在Q 上的阻尼高斯-牛顿法和信赖域正则化的遗传算法[14-16]。为克服步长较大引起的计算误差增加的问题,阻尼高斯-牛顿法采用保持迭代步的方向不变的前提下缩短步长的方法,而具有全局收敛性的信赖域正则化遗传算法不仅限制步长,且获得新的收敛方向。通过设置信赖域的大小而及时改变迭代方向,基于遗传算法优化模拟电荷空间位置,信赖域正则化遗传算法比Levenberg-Marquardt 法、阻尼高斯-牛顿法具有较快的收敛速度和更少迭代的次数。因此,基于信赖域正则化遗传算法计算复杂导线垂直断面地势下直流线路无线电干扰具有较好的收敛性和稳定性。
为进一步验证信赖域正则化遗传算法的精度,选取3个云广特高压直流线路垂直断面,分别开展信赖域正则化遗传算法的理论计算和现场测量的误差精度分析。
断面 1 正极导线对地高度为 33m,海拔高度64m,温度 31~34.4ºC,湿度 54%~65%,风速0.5m/s,断面1 所处线路档距内沿线路平行方向的地形峰谷差最大为0.6m,断面1 的无线电干扰背景是按标准规定在线路带电时距离线路400m 以外的测量值为23.6dB,满足无线电干扰背景至少比线路无线电干扰值低10dB 的要求。断面1 仿真计算结果与测量值分布如图4 所示。由图4 可知,未考虑地势起伏影响的马克特-门格尔法和逐步镜像法(传统电力线路设计)计算结果具有两极正下方的无线电干扰值最大,两极之外的区域呈衰减趋势,两极之间是先衰减后增加的规则分布,同时其计算结果小于现场测量值。而信赖域正则化遗传算法计算该断面的无线电干扰整体分布规律与现场测量值的大小基本一致。
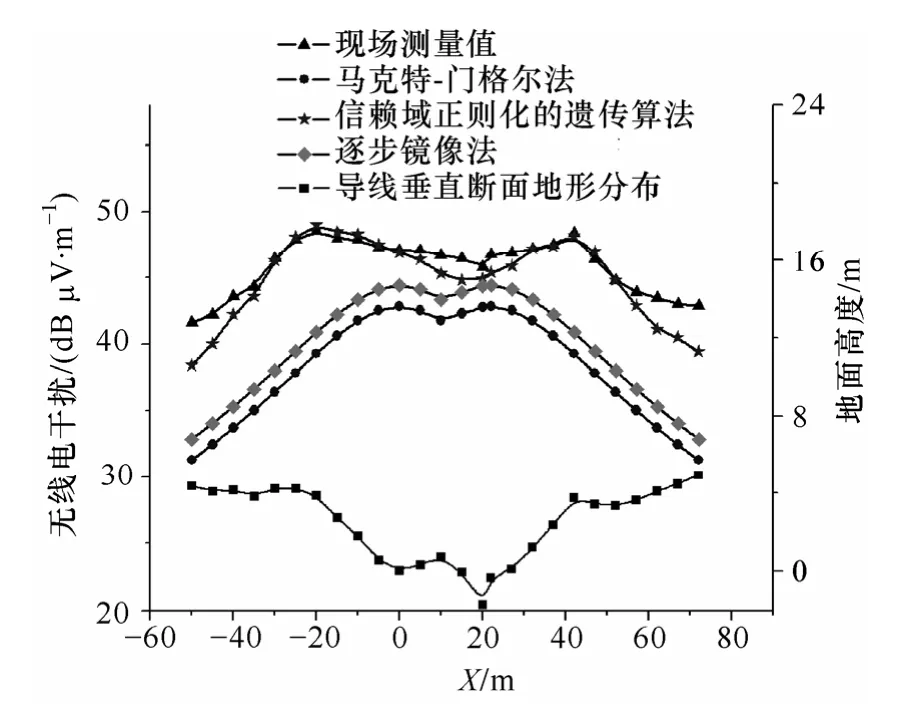
图4 断面1 理论计算结果与测量值分布Fig.4 The distribution of simulation and measurement RI for section 1
断面 2 正极导线对地高度为 49m,海拔高度700m,温度32.9~36.5ºC,湿度43%~52%,风速1m/s,断面2 所处线路档距内沿线路平行方向的地形峰谷差最大为0.5m,断面2 的无线电干扰背景是按标准规定在线路带电时距离线路400m 以外的测量值为27.1dB,满足无线电干扰背景至少比线路无线电干扰值低10dB 的要求。因断面2 的海拔高度是 700m,同时海拔高度增加会使导线起晕电压降低,使无线电干扰增加。根据国外海拔修正方法(海拔每增加1 000m,无线电干扰增加3.3dB)进行马克特-门格尔法、逐步镜像法和信赖域正则化遗传算法计算结果的修正[17]。断面2 理论计算结果与测量值分布如图5 所示,与断面1 的马克特-门格尔法和逐步镜像法计算结果相比,无线电干扰计算结果分布平缓。同时信赖域正则化遗传算法的计算结果与测量值的分布具有相同的规律,其相对误差明显小于马克特-门格尔法和逐步镜像法。信赖域正则化遗传算法计算结果海拔修正前的无线电干扰分布与测量值的最大和最小误差分别为8%和1%,然而海拔修正后的无线电干扰分布与测量值的最大和最小误差分别为3%和0.03%。因此对于断面2 的信赖域正则化遗传算法计算结果进行海拔修正能够获得与测量值更小的误差。

图5 断面2 理论计算结果与测量值分布Fig.5 The distribution of simulation and measurement RI for section 2
断面3 正极导线对地高度为36.5m,海拔高度1 900m,温度16.4~33.6ºC,湿度58%~70%,风速0.4m/s,断面3 所处线路档距内沿线路平行方向的地形峰谷差最大为0.7m,断面3 的无线电干扰背景是按标准规定在线路带电时距离线路400m 以外的测量值为20.4dB,满足无线电干扰背景至少比线路无线电干扰值低10dB 的要求,同时将断面2 的海拔修正方法用于断面3 的数据修正。断面3 理论计算结果与测量值分布如图6 所示,相对断面1、2而言,断面3 的海拔高度更高,因测点地势起伏的影响,相对马克特-门格尔法和逐步镜像法在正极和负极地面投影处获得最大无线电干扰而言,现场测量值的最大值位置发生了偏移。同时断面3 信赖域正则化遗传算法仿真值小于测量值但大于马克特-门格尔法和逐步镜像法的仿真值。考虑海拔高度对导线起晕电压和无线电干扰的影响,其修正结果与现场测量值具有极好的吻合度。断面3 的海拔修正结果也提高了高海拔下信赖域正则化遗传算法的计算精度。
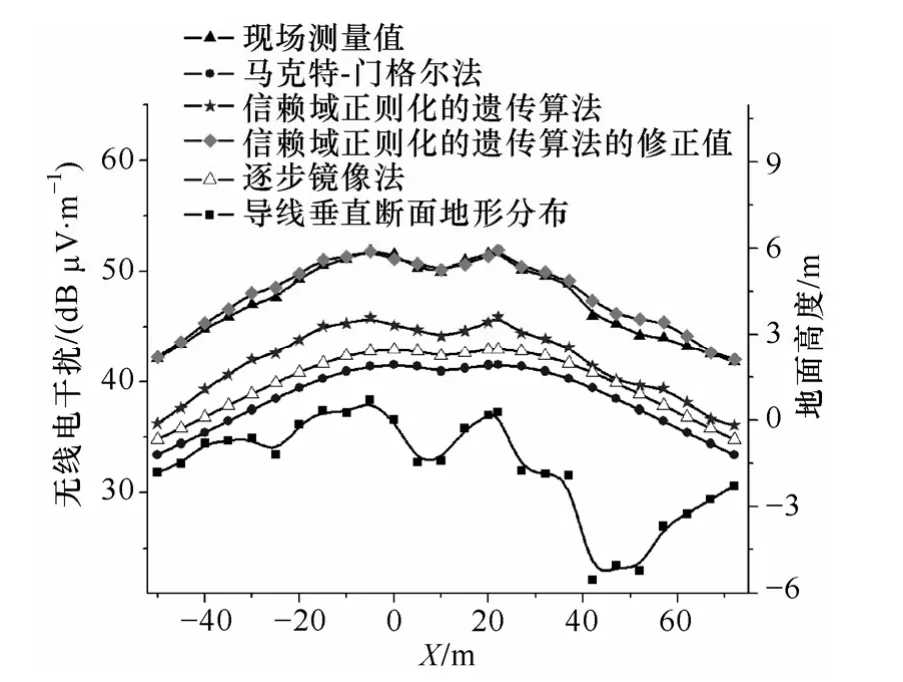
图6 断面3 理论计算结果与测量值分布Fig.6 The distribution of simulation and measurement RI for section 3
4 结论
本文针对目前复杂导线垂直断面地势下直流线路无线电干扰计算方法的不足,提出了信赖域正则化遗传算法,建立了复杂导线垂直断面地势下直流线路无线电干扰计算模型。基于本文物理建模、算法原理、现场测量和仿真结果得出以下结论:
(1)提出了信赖域正则化遗传算法优化直流线路电场计算的模拟电荷空间位置和电荷量。当线路单一档距内沿线路方向的地势较平坦时,该方法对于实际线路所处复杂导线垂直断面地势比传统设计方法更具适应性。
(2)通过设置信赖域的大小和迭代方向,信赖域正则化遗传算法比Levenberg-Marquardt 法、阻尼高斯-牛顿法分析复杂导线垂直断面地势下直流线路无线电干扰具有更好的收敛性和稳定性。
(3)通过实际复杂导线垂直断面地势下直流线路无线电干扰仿真计算和现场测量值的比较分析,信赖域正则化遗传算法的计算值分布规律与测量值基本一致。当海拔高度较低时计算精度高,但海拔高度较高时需利用海拔每增加1 000m 无线电干扰增加3.3dB 的方法进行修正。该方法能较准确地预测复杂导线垂直断面地势下直流线路无线电干扰分布,为输电线路电磁环境评估和计算提供了有效的数值方法,对复杂导线垂直断面地势下线路设计和改造具有工程应用价值。
[1]吴敬儒,徐永禧.我国特高压交流输电发展前景[J].电网技术,2005,29(3):1-4.Wu Jingru,Xu Yongxi.Development prospect of UHV AC power transmission in China[J].Power System Technology,2005,29(3):1-4.
[2]施春华,朱普轩,蒋剑,等.±800kV 特高压直流线路采用5 分裂导线的电磁环境特性分析[J].高电压技术,2011,37(3):666-671.Shi Chunhua,Zhu Puxuan,Jiang Jian,et al.Electromagnetic environment profile of ±800kV UHVDC transmission lines using 5 bundled conductors[J].High Voltage Engineering,2011,37(3):666-671.
[3]薛志方,程思勇,何民,等.糯扎渡-广东±800 kV直流输电线路导线选型[J].高电压技术,2009,35(10):2344-2349.Xue Zhifang,Cheng Siyong,He Min,et al.Conductor schemes for ±800kV UHVDC transmission line of Nuozhadu-Guangdong[J].High Voltage Engineering,2009,35(10):2344-2349.
[4]张文亮,陆家榆,鞠勇,等.±800kV 直流输电线路的导线选型研究[J].中国电机工程学报,2007,27(27):1-6.Zhang Wenliang,Lu Jiayu,Ju Yong,et al.Design consideration of conductor bundles of ±800kV DC transmission lines[J].Proceedings of the CSEE,2007,27(27):1-6.
[5]孟晓波,卞星明,陈枫林,等.负直流下绞线电晕起始电压分析[J].高电压技术,2011,37(1):77-84.Meng Xiaobo,Bian Xingming,Chen Fenglin,et al.Analysis on negative DC corona inception voltage of stranded conductors[J].High Voltage Engineering,2011,37(1):77-84.
[6]关志成,陈枫林,卞星明,等.高海拔条件下钢芯铝绞线的正直流电晕起始电压分析[J].高电压技术,2011,37(4):809-816.Guan Zhicheng,Chen Fenglin,Bian Xingming,et al.Analysis on onset voltage of positive corona on stranded conductors in high-altitude condition[J].High Voltage Engineering,2011,37(4):809-816.
[7]李敏,余占清,曾嵘,等.高海拔±800 kV 直流输电线路电磁环境测量[J].南方电网技术,2011,5(1):42-45.Li Min,Yu Zhanqing,Zeng Rong,et al.Electromagnetic environment measurement of ±800kV DC transmission lines at high altitude[J].Southern Power System Technology,2011,5(1):42-45.
[8]周宏威,左鹏,邹军,等.复杂地形情况下高压交流输电线路电磁环境特性分析[J].电网技术,2011,35(9):164-169.Zhou Hongwei,Zuo Peng,Zou Jun,et al.Analysis on electromagnetic environment characteristics of highvoltage AC transmission lines passing through complex terrains[J].Power System Technology,2011,35(9):164-169.
[9]俞集辉,周超.复杂地势下超高压输电线路的工频电场[J].高电压技术,2006,32(1):18-20.Yu Jihui,Zhou Chao.Power-frequency electric field of EHV transmission lines under condition of complex landscape[J].High Voltage Engineering,2006,32(1):18-20.
[10]彭一琦.考虑气象条件的输电导线工频电场计算新方法[J].高电压技术,2010,36(10):2507-2511.Peng Yiqi.Novel method for transmission line power frequency electric field calculation considering the weather condition[J].High Voltage Engineering,2010,36(10):2507-2511.
[11]陈楠,文习山,蓝磊,等.基于电场逆运算的输电导线弧垂计算方法[J].中国电机工程学报,2011,31(16):121-127.Chen Nan,Wen Xishan,Lan Lei,et al.Novel algorithm for transmission line sag calculation based on electrical field invert arithmetic[J].Proceedings of the CSEE,2011,31(16):121-127.
[12]赵畹君.高压直流输电工程技术[M].北京:中国电力出版社,2004.
[13]陈磊.遗传最小二乘支持向量机法预测时用水量[J].浙江大学学报(工学版),2011,45(6):1100-1104.Chen Lei.Genetic least squares support vector machine approach to hourly water consumption prediction[J].Journal of Zhejiang University(Engineering Science),2011,45(6):1100-1104.
[14]Armijo L.Minimization of function having Lipschitz continuous first partial derivatives[J].Pacific Journal of Mathematics,1966,16(1):1-3.
[15]Taylor D G.Song Li.Damped Gauss-Newton method for direct stable inversion of continuous-time nonlinear systems[C].The 29th Annual Conference of the IEEE,Roanoke,Virginia,USA,2003:606-610.
[16]Sande H V,De G H.Solving nonlinear magnetic problems using Newton trust region methods[J].IEEE Transactions on Magnetics,2003,39(3):1709-1712.
[17]EPRI.HVDC transmission line reference book[M].Palo Alto,California,USA:EPRI,1993.

