输入电压不平衡时三相PFC 整流器改进单周期控制策略研究
韦 徵 陈 新 陈 杰 龚春英 樊 轶
(南京航空航天大学自动化学院 南京 210016)
1 引言
由于供电系统和用电设备中输入电源的多样性,改善PFC 整流器的性能,减小输入电流谐波含量,提高系统的功率因数具有重要意义[1-4]。
单周期控制的PFC 变换器无需产生输入电流基准,因而不需要使用乘法器和采样输入电源电压,简化了控制结构,降低了经济成本,在中小功率场合得到了广泛的应用。在三相输入电源平衡时,文献[5-9]对三相 PFC 整流器的单周期控制策略进行了分析和研究,表明单周期控制的三相PFC 整流器具有动态响应快、开关频率稳定、输入电流畸变率低、易于实现等优点。但在实际应用中,由于输入电源通常并非理想的对称电压源,在这种情况下,传统单周期控制理论下的三相PFC 变换器输入电流将会产生较大的三次谐波分量,从而影响输入电流THD(total harmonic distortion)。文献[10]针对这一现象提出增大整流器直流侧输出电容,通过平滑直流侧输出电压,进而达到改善输入电流THD 的目的。但此方法将显著增加变换器成本以及体积重量,不利于提高系统功率密度。文献[11]引入了电压不对称系数概念,通过采样输入电压计算得到不对称系数,并用该系数对各相输入电流的采样值进行调整,从而改善输入电流品质。但是该方案需要采样三相电源电压,并需要进行较复杂的数学运算,增加了控制系统复杂性,且只能采用数字控制。
本文通过分析三相PFC 整流器中的三相三开关VIENNA 整流器在输入不平衡时的输入输出特性,提出在三相PFC 整流器传统单周期控制策略中引入谐振控制器。新控制电路简单,无需增加采样三相电源电压且在模拟或数字控制中均易实现。当三相输入不平衡时,改进后单周期控制策略可以有效抑制三相输入电流中较大幅值的三次谐波分量,从而可以大大改善整流器输入电流波形质量。同时,改进的单周期控制策略可推广至其他三相PFC 变换器。系统仿真与实验表明了理论分析的正确性。
2 三相VIENNA 整流器传统单周期控制
图1a 所示为三相三开关VIENNA 整流拓扑,其中eA、eB、eC为变换器三相输入电源,iLA、iLB、iLC为三相输入电流,L为三相输入滤波电感,Cf为直流侧滤波电容,UC1、UC2分别为输出滤波电容的端电压,Udc为输出直流电压,RL为输出负载电阻。令开关管S1、S2、S3的占空比分别为dA、dB、dC。
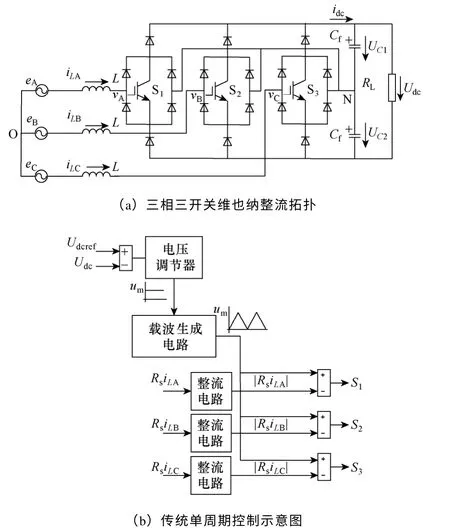
图1 三相三开关VIENNA 整流器及其控制示意图Fig.1 Three-phase three switches VIENNA rectifier and conventional one-cycle control scheme
从系统电源输入侧看,单位功率因数时的三相输入阻抗可以等效为纯电阻负载,故系统的控制目标为

式中,Re为系统单位功率因数补偿后,反映负载大小的三相等效输入电阻。从而由文献[12]可得三相VIENNA 整流器单周期控制方案的核心控制方程为

式中,um=UdcRs/2Re为电路工作稳态时的电压调节器输出值;Rs为输入电流的采样电阻。其单周期控制电路示意图如图1b 所示。主要由电压调节器,载波生成电路以及脉宽调制环节组成。其中载波生成电路可由带复位的积分器,脉冲发生器等模拟器件构成实现。
3 输入不平衡时的三相VIENNA 整流器输入输出特性分析
令SA、SB、SC为各相桥臂的开关函数,忽略开关周期内的电感压降[12],从而可得
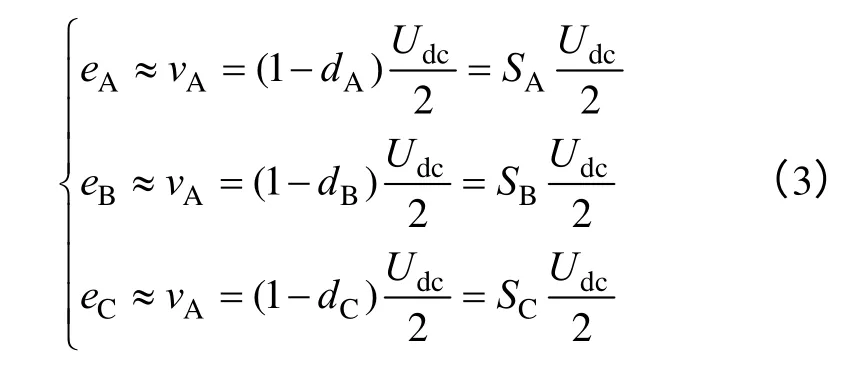
根据图1a 所示的三相VIENNA 整流器拓扑,忽略变换器功率损耗,由变换器输入交流侧与输出直流侧瞬时功率守恒可得
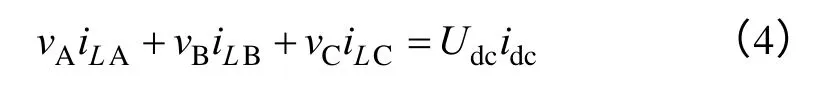
联立式(3)、式(4)可得
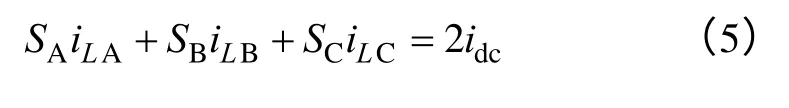
当三相输入不平衡时,令变换器三相输入电流基波为
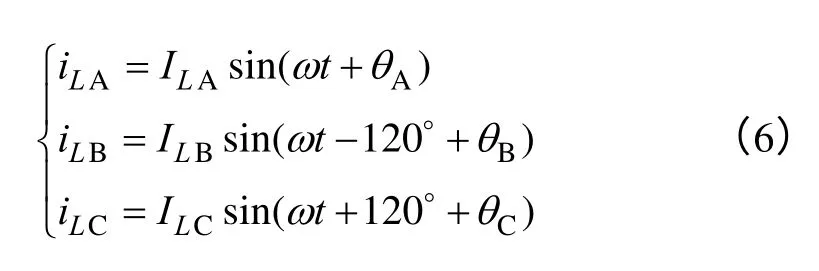
式中,ILA、ILB、ILC为各相输入电流基波的峰值;θA、θB、θC为各相输入电流基波的初始相位;ω为输入基波角频率。
令各相桥臂的开关函数的傅里叶展开式为
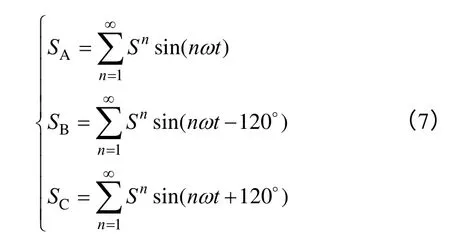
式中,Sn为开关函数各次谐波分量。
结合式(5)~式(7)可得
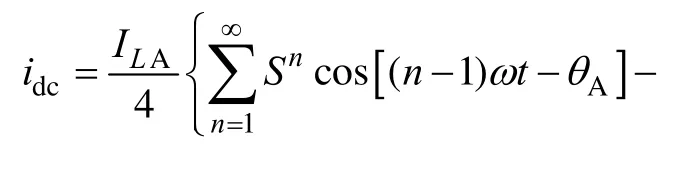
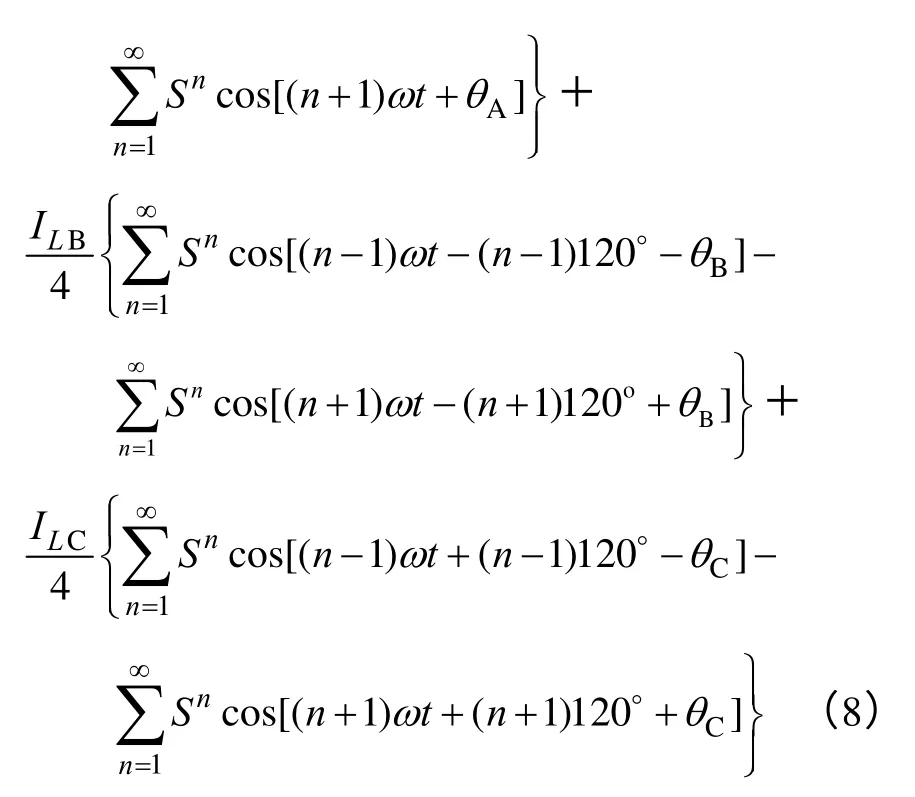
由式(8)可以看出,当输入不平衡时,通过三相VIENNA 整流器输入侧交流电流的基波分量与各相桥臂开关函数的相互作用,将导致输出直流侧产生输入基波频率的2、4、8 等倍次谐波分量,且其谐波幅值与输入不平衡程度相关。其中2 次谐波分量为
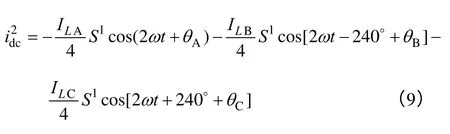
伴随输出直流产生输入基波频率的2、4、8 等倍次谐波分量,直流侧输出电压亦产生相应倍次谐波。在传统的单周期控制策略中,为保证整流器的稳压精度和动态响应性能,电压调节器的低频增益一般均较大。因此在控制环路中,输出直流电压采样中所含有的2 次谐波分量经过电压调节器得到放大,从而使得调节器输出信号亦含有相应的2 次谐波分量。
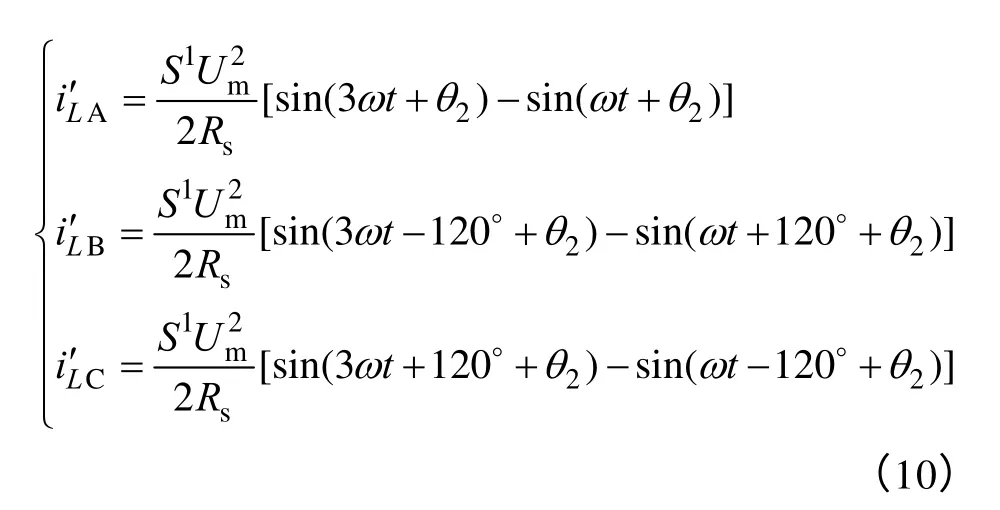
式(10)表明,当整流器三相输入不平衡时,传统单周期控制方案中的电压调节器输出所含有的两倍于输入电源基波频率的脉动信号作为载波的幅值并与三相电流采样信号相交割产生控制开关管的占空比信号,将导致整流器三相输入电流产生3 次谐波分量,进而增加输入电流的畸变程度,影响输入电流的波形质量。
4 输入不平衡时,三相VIENNA 整流器改进单周期控制策略
4.1 改进单周期控制策略
根据上述理论分析,可得知当输入不平衡时,三相VIENNA 整流器输出直流侧将产生2 倍于输入电源频率的谐波分量。该谐波分量经过传统单周期控制环路的作用,最终将导致整流器三相输入电流产生3 次谐波分量。为此,本文提出在传统的单周期控制策略中引入谐振控制器,同时为保证整流器直流侧两个输出滤波电容均分输出电压,在原有控制环路中加入均压环,改进的单周期控制方案框图及谐振控制器引入的具体位置如图2a 所示。该谐振控制器仅对电压调节器输出信号中所含有的2 次谐波分量进行衰减,其他频段的信号不受影响,从而使得载波幅值中所含有相应的2 次脉动分量得以抑制,最终大大削减了输入电流中的3 次谐波分量,改善了输入电流品质。模拟谐振控制器内部结构如图2b 所示。

图2 改进单周期控制策略及谐振控制器结构示意图Fig.2 Modified one-cycle control scheme and structure of resonant controller
4.2 谐振控制器工作分析
根据图2b 所示的模拟谐振控制器结构图,可得其传递函数为

内部元件参数关系为

式(14)所示的谐振控制器传递函数中,ω为谐振频率,根据上述关于输入不平衡时,三相VIENNA 整流器工作特性的分析可知,此谐振频率设置与整流器三相输入电源基波频率相关,即该谐振频率应为三相输入电源基波频率的2 倍。如当整流器输入电源频率为400Hz 时,整流器输出直流电压含有800Hz 的脉动分量,从而单周期控制系统中的电压调节器输出的误差电压放大信号中也含有相应的800Hz 脉动分量。因此谐振控制器传递函数中ω=5 024rad/s。
当ω取5 024rad/s,谐振控制器传递函数中Q值分别取0.5(G1)、1(G2)、5(G3)时,对应传递函数的伯德图如图3 所示。由图3 可以看出,Q取不同值的时候,谐振控制器对所需要滤除的指定频率的分量效果也不同。Q值越小,谐振控制器对输入信号的衰减频带越宽。此外,谐振控制器仅对指定频率处的信号具有强抑制作用,对其他频段内的信号没有影响。

图3 谐振控制器传递函数伯德图Fig.3 The bode plot of resonant controller
当采用数字电路实现系统控制策略时,所提出的谐振控制器可先通过双线性变换将式(14)所示的传递函数进行离散化,从而获得z域上的谐振控制器传递函数为

式中,T为数字电路中的信号采样周期。
将离散后的谐振控制器z域上的传递函数进一步写成差分方程,即可方便通过数字实现。
4.3 系统传递函数及稳定性设计
引入谐振控制器后,以一相为例,单周期控制的三相VIENNA 整流器系统控制结构图如图4 所示。

图4 三相VIENNA 整流器系统控制结构图Fig.4 Control block diagram for the VIENNA rectifier
图4 中Hv为输出电压采样系数;Gv(s) 为电压调节器传递函数;Gmi(s)为载波幅值-直流侧输出电流传递函数[13];Zo(s) 为直流侧输出电流-输出电压传递函数。
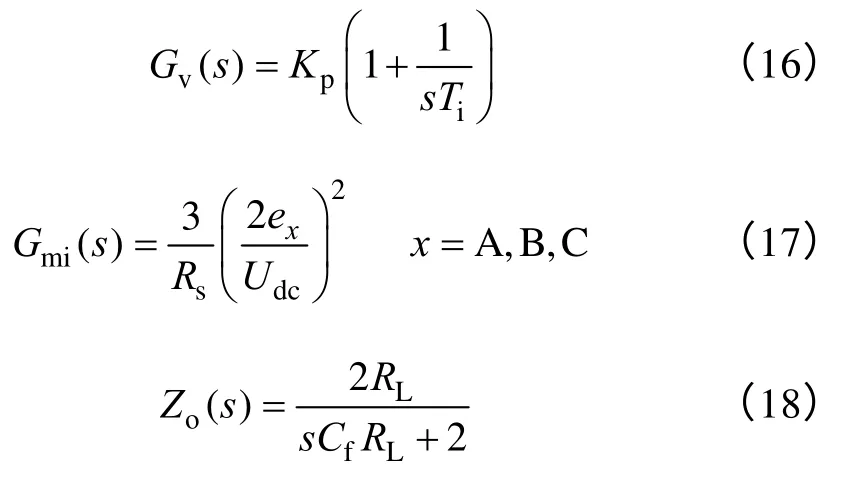
由控制框图可得系统电压环开环增益为
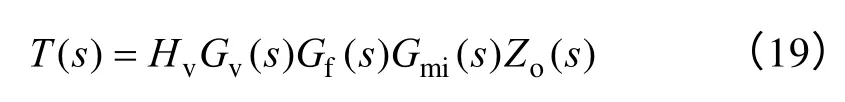
根据系统稳定性要求,当系统闭环运行时,整个系统环路增益要满足相位裕度大于45°,幅值裕度大于6dB 以确保系统稳定性[14]。因此,电路中相关控制参数的选择亦需考虑到上述原则。
5 仿真及实验验证
对所提出的控制策略在2.5kW 三相VIENNA 整流器样机中进行了实验验证。电路具体参数为:整流器输入电源频率为 400Hz,输出直流电压为350V,输出电压采样系数为0.01,输入电流等效采样电阻为0.1Ω,开关频率50kHz,三相输入滤波电感为1.5mH,输出滤波电容为470µF,主开关元件采用IXFK64N50P,整流二极管采用DSEP60-04A。
根据上述的系统稳定性原则,合理选取电压控制器、谐振控制器各个元器件参数,并利用Matlab软件计算出系统电压环开环增益T(s) 的伯德图,如图5 所示。从中可以看出,根据所选取的参数,使得系统开环增益均有足够的相位裕度,其裕度为60°左右,从而保证整个系统工作稳定。此外,引入谐振控制器后的系统开环幅频特性曲线在频率为800 Hz 处的增益有较大的衰减,从而保证可以有效抑制输入不平衡时,控制环路中存在的2 倍于输入电源频率的脉动信号,进而抑制整流器输入电流中所含有的3 次谐波分量。
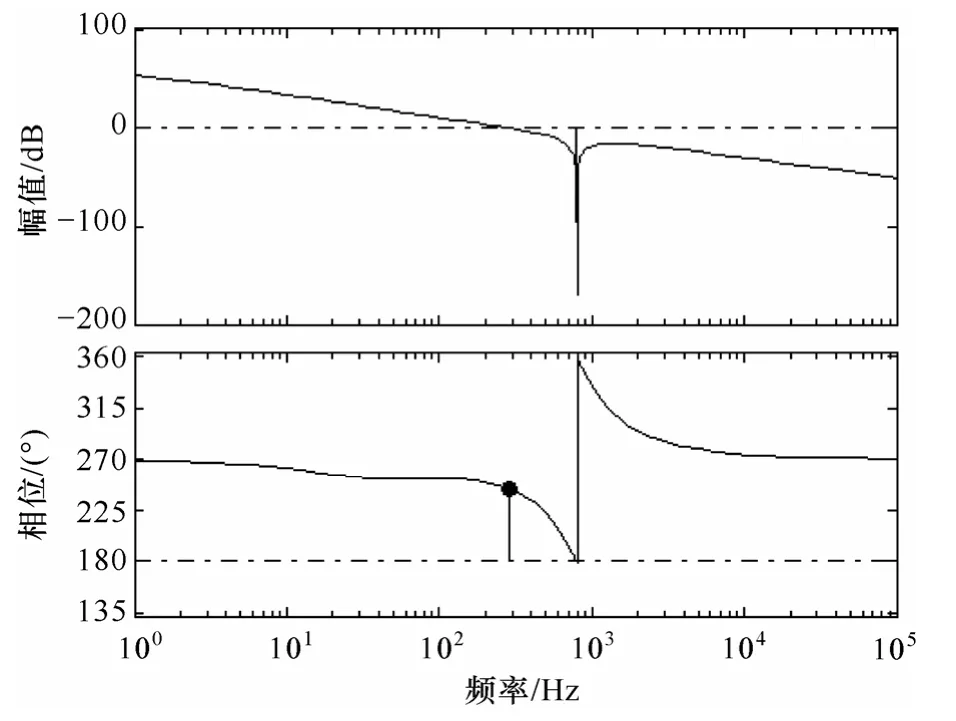
图5 系统开环增益伯德图Fig.5 System open-loop gain bode plots
当变换器三相输入电压为115V±20V 不平衡,以及115V±50V 不平衡时,图6 给出传统单周期控制下的三相VIENNA 整流器一相不平衡输入电压及三相输入电流,电压调节器输出信号的仿真波形。可以看出,当输入不平衡时,整流器电压调节器输出信号含有2 倍于输入电源频率的脉动分量,且该脉动分量的幅值随变换器输入电源不平衡程度的增加而增大,从而使得三相输入电流产生畸变。

图6 未引入谐振控制器前系统仿真波形Fig.6 System simulation waveforms before introduction of resonant controller
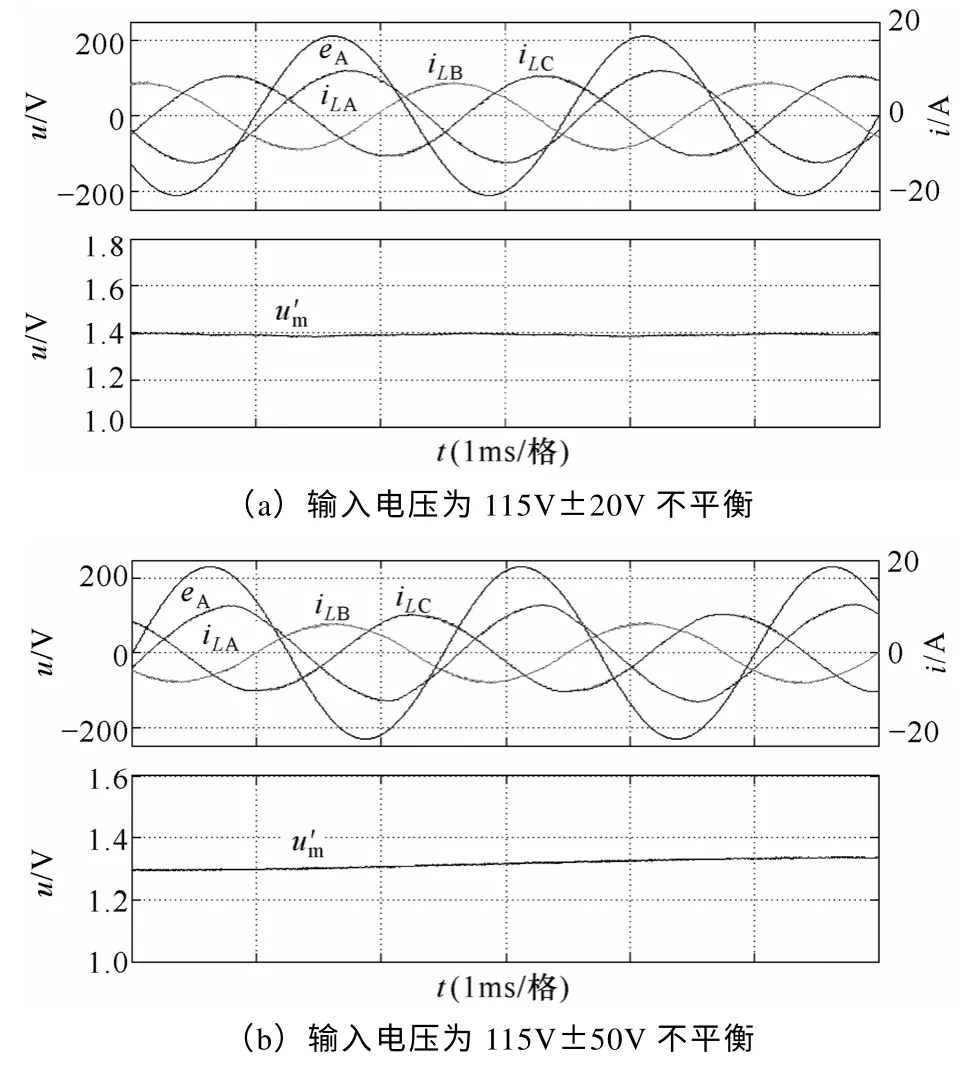
图7 引入谐振控制器前后系统仿真波形Fig.7 System simulation waveforms after introduction of resonant controller
图7 为引入谐振控制器后,不同输入电压不平衡程度下的改进单周期控制三相VIENNA 整流器对应点的仿真波形。从中可以看出,当输入不平衡所导致的电压调节器含有2 倍于输入电源频率的脉动分量经过谐振控制器后被很好的抑制住,从而使得单周期控制的整流器输入三相电流THD 得到很好的改善。同时,由于输入电源不平衡程度的增加,为了达到良好的抑制效果,减小输入电流的THD,谐振控制器参数需要进行相应的调整,以满足对谐振频率点处具有更强的衰减能力。需要指出的是,从仿真波形可以看出,输入电感电流滞后于对应相的输入电源电压相位。这是由于当前输入电源频率为400Hz,电源频率与开关频率比值较小,此时单周期控制的整流器的工作状态不能完全等效为准稳态工作,从而造成输入电感电流存在基波相移[15]。
图8 进一步给出了相关实验波形。其中图8a为三相输入电源电压分别为 AC95V、AC115V 及AC135V 时,一相不平衡输入电压及三相输入电流波形,图8b 为三相输入电流频谱图。可以看出,当输入不平衡时,三相输入电流产生畸变,实测表明三相输入电流THD 分别为3.46%、3.55%、3.9%。频谱分析显示输入电流含有较大幅值的3 次谐波分量。
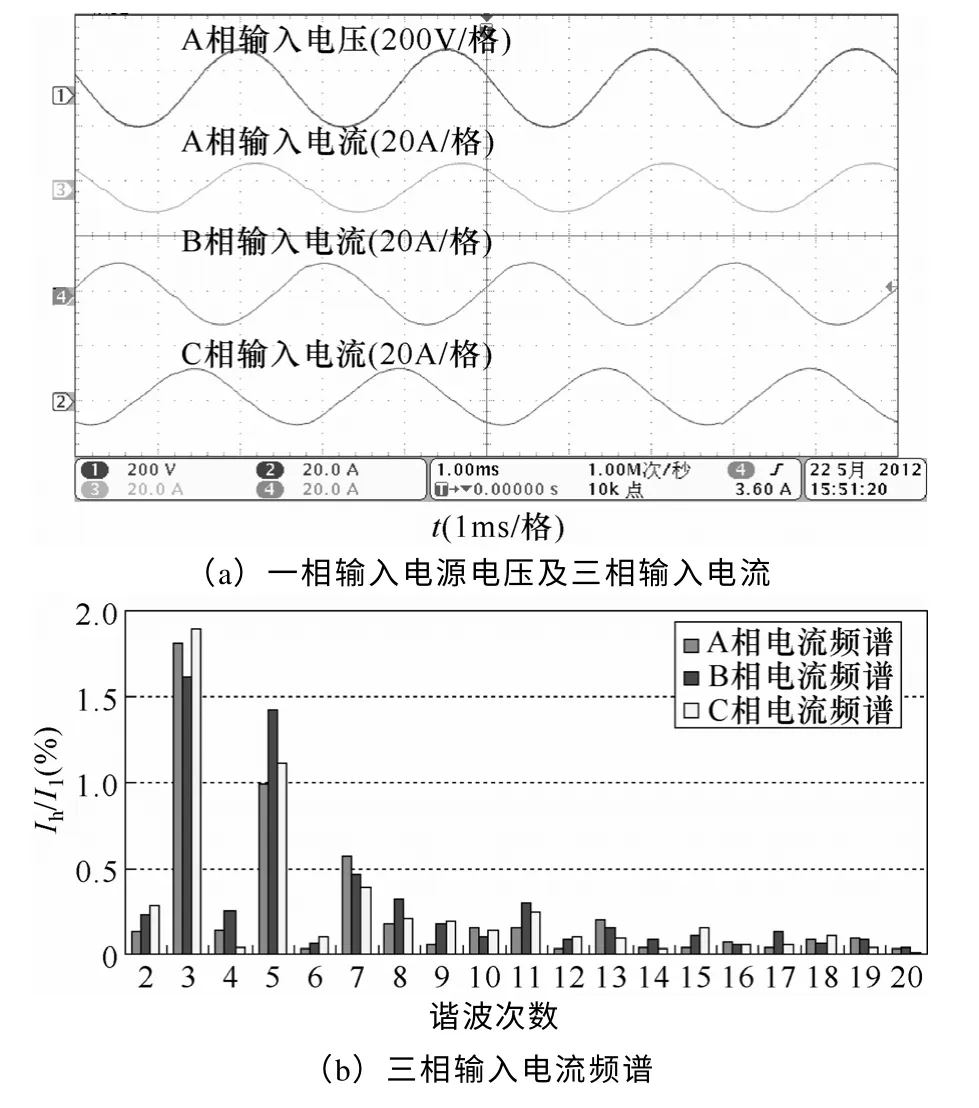
图8 引入谐振控制器前整流器实验波形及输入电流频谱Fig.8 Experimental waveforms and input current spectrum before introduction of resonant controller
图9a 为引入谐振控制器后,同样实验条件下一相不平衡输入电压及三相输入电流波形,图9b 为三相输入电流频谱图。波形显示,在引入谐振控制器后,输入电压不平衡条件下的变换器三相输入电流THD 下降,实测表明三相电流THD 分别为2.6%、2.8%、2.5%。频谱分析进一步表明电感电流中的3次谐波分量大大减小。
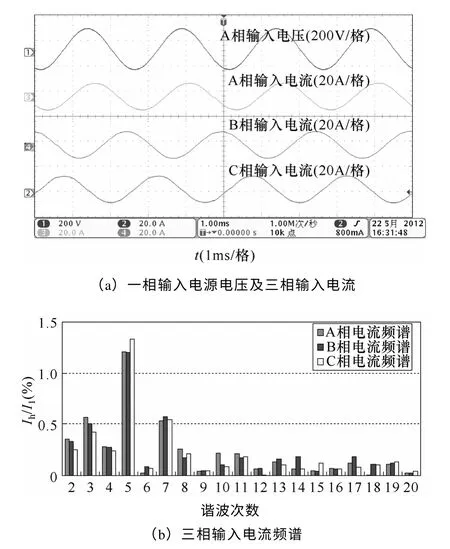
图9 引入谐振控制器后,整流器实验波形及输入电流频谱Fig.9 Experimental waveforms and input current spectrum after introduction of resonant controller
图10 为输出负载功率由1.5kW 突加至2.5kW时,变换器动态实验波形。波形显示在负载突加过程中,整流器输出电压均很好的稳定在给定的350V,在所提出的控制策略下,变换器具有良好的动态特性。
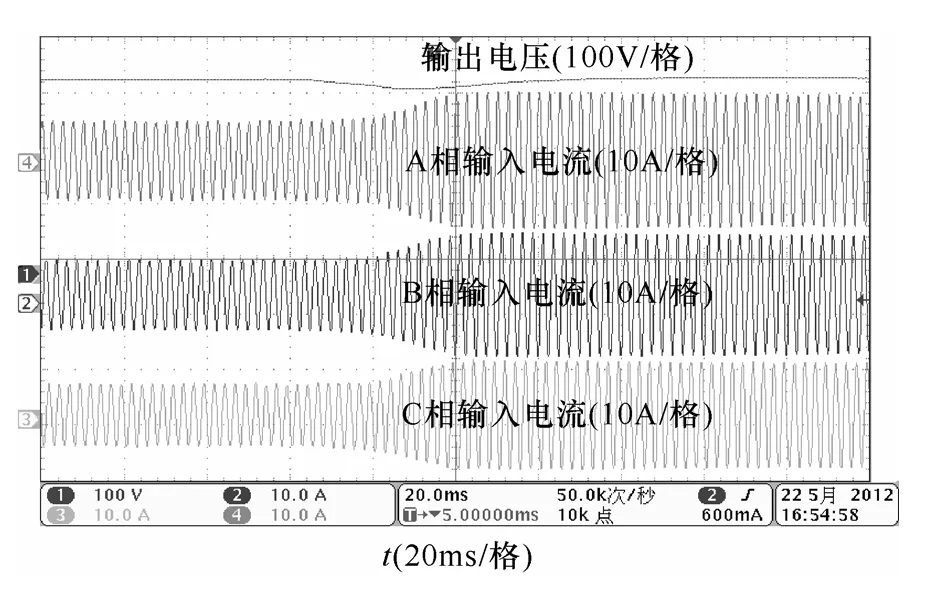
图10 整流器动态实验波形Fig.10 Dynamic experimental waveforms
6 结论
(1)当输入不平衡时,三相PFC 整流器输出直流侧将产生2 倍于输入电源频率的脉动分量。在传统单周期控制策略下,电压调节器输出信号同样存在相应频率的脉动信号。以该脉动信号作为载波的幅值并与整流器三相电流采样信号相交割产生控制开关管的占空比信号,从而导致整流器三相输入电流产生较大幅值的3 次谐波分量,进而影响输入电流的波形质量。
(2)本文提出在传统的单周期控制策略中引入谐振控制器,可以有效抑制整流器输出直流侧的2倍于输入电源频率的脉动分量对于输入电流的影响,从而大大改善了输入电流的波形质量。所提出的控制电路简单易实现,仿真与实验结果充分表明理论分析的正确性。
[1]方宇,裘迅,邢岩,等.三相高功率因数电压型PWM 整流器建模和仿真[J].电工技术学报,2006,21(10):44-49.Fang Yu,Qiu Xun,Xing Yan,et al.Modeling and simulation of three phase high power factor PWM rectifier[J].Transactions of China Electrontechnical Society,2006,21(10):44-49.
[2]Luigi Malesani,Paolo Tomasin,Vanni Toigo.Space vector control and current harmonics in quasi-resonant soft-switching PWM conversion[J].IEEE Transactions on Industry Applications,1996,32(2):269-277.
[3]Mobin S,Hiraki E,Takano H,et al.Simulation method for DSP-controlled active PFC high-frequency power converters[J].IEEE Electric Power Applications,2000,147(3):159-166.
[4]Noguchi T,Tomiki H,Kondo S.Direct power control of PWM converter without power-source voltage sensor[J].IEEE Transactions on Industry Applications,1998,34(3):473-479.
[5]Lai Zheren,Smedley K M.A family of continuous conduction mode power factor correction controllers based on the general pulse-width modulator[J].IEEE Transactions on Power Electronics,1998,13(3):501-510.
[6]Qiao Chongming,Smedley K M.A general threephase PFC controller for rectifiers with a parallelconnected dual boost topology[J].IEEE Transactions on Power Electronics,2002,17(6):925-934.
[7]Qiao Chongming,Smedley K M.A general threephase PFC controller for rectifiers with a seriesconnected dual boost topology[J].IEEE Transactions on Power Electronics,2002,38(1):137-148.
[8]Rajesh Ghosh,Narayanan G.A simple analog controller for single-phase half-bridge rectifier[J].IEEE Transactions on Power Electronics,2007,22(1):186-198.
[9]Rajesh Ghosh,Narayanan G.Control of three-phase four-wire PWM rectifier[J].IEEE Transactions on Power Electronics,2008,23(1):96-106.
[10]Taotao Jin,Smedley K M.Operation of one-cycle controlled three-phase active power filter with unbalanced source and load[J].IEEE Electric Power Applications,2006,21(5):1403-1413.
[11]金爱娟,李航天,李少龙.基于单周期控制的三相PFC 整流器在输入电压不对称时的改进策略[J].电工技术学报,2006,21 (7):115-121.Jin Aijuan,Li Hangtian,Li Shaolong.An improved control strategy of the one-cycle control three-phase PFC rectifier under unbalanced conditions[J].Transactions of China Electrontechnical Society,2006,21(7):115-121 .
[12]Qiao Chongming,Smedley K M.Three-phase unitypower-factor star-connected switch(VIENNA) rectifier with unified constant-frequency integration control[J].IEEE Transactions on Power Electronics,2003,18(4):952-958.
[13]毛鹏,谢少军,许泽刚.开关频率与电源频率比值较小时单周期控制PFC 变换器的建模及稳定性[J].电工技术学报,2010,25(4):82-89.Mao Peng,Xie Shaojun,Xu Zegang.Modeling and stability analysis of OCC PFC converter with low ratio of switching frequency to power frequency[J].Transactions of China Electrotechnical Society,2010,25(4):82-89.
[14]Ridley R B,Cho B H,Lee F C.Analysis and interpretation of loop gains of multi-loop-controlled switching regulators[J].IEEE Transactions on Power Electronics,1988,3(4):489-498.
[15]毛鹏,谢少军,许爱国,等.单周期控制PFC 变换器电流相位滞后及其补偿[J].电工技术学报,2010,25(12):111-118.Mao Peng,Xie Shaojun,Xu Aiguo,et al.Current phase lag compensation for one cycle controlled PFC converter[J].Transactions of China Electrotechnical Society,2010,25(12):111-118.

