基于状态观测器的LCL 滤波器型并网逆变器状态反馈最优化设计

李 宾 姚文熙 杭丽君 吕征宇

（浙江大学电力电子国家专业实验室 杭州 310027）

1 引言

当今社会，化石燃料燃烧造成的环境污染以及非可再生资源的不断消耗所带来的能源危机，使得可再生能源的开发变得非常重要。风能、地热能、燃料电池以及太阳能等新能源不断兴起，并在分布式发电（Distributed Generation,DG）中占据越来越多的份额[1-3]。

这些新能源都要通过并网逆变器来向电网馈能。并网逆变器一般采用脉冲宽度调制（Pulse Width Modulation,PWM）下的电流型控制，因此会有很多含有高频谐波的电流进入电网，影响电网质量。为了滤除高频电流，通常要在逆变器与电网之间加入电感。相对于传统的L 型滤波器，LCL 滤波器通过电容支路提供高频旁路从而显著衰减流入电网电流的高频分量，因此被广泛使用于大功率设备[4-6]。但由于LCL 本身存在谐振，在实际的控制过程中需要阻尼来抑制其谐振。传统的阻尼方法一般是在电感或电容上串联电阻（Passive Damping,DP）[7,8]。但是这种方法不仅增大了系统的损耗，还削弱了LCL滤波器的性能[8]。为了解决这一问题，许多学者提出通过不同的控制方式进行有源阻尼（Active Damping,AD）[8-17]。文献[9-12]分别利用电容电压和电容电流反馈进行阻尼；文献[13]则提出了一种基于虚拟电阻（virtual resistor）的解决方案。但是这三种方法都要增加传感器的数量，增加了系统成本。文献[8]通过加入A-D 模块来改善系统的性能；文献[14,15]则提出了一种分裂电容的方法，通过采集两个电容之间的电流进行阻尼。虽然这两种方法在不增加系统成本的前提下达到了阻尼LCL 谐振的效果，但对于系统的动态响应却没有明确的改善，而且对LCL 参数要求很高。相对于前述几种使用传统伯德图理论的分析，极点配置理论[18]能够更好的解释系统的动态性能，因此一种基于状态空间的极点配置方法被提了出来[16,17]，这种方法通过配置闭环极点的位置来改善系统的动态响应和稳态波形，取得了不错的效果。观测器[18]能够通过系统中可测量的值得到系统中不可测量的值，因此观测器的采用可以有效减少传感器的数量。文献[19-21]设计了基于LCL 型并网逆变器的观测器，但并没有说明闭环极点位置对观测器极点配置的影响以及观测量反馈的稳定性，同时也没有验证系统的动态响应。而且文献[21]没有考虑到系统延时以及滤波器参数对系统极点的影响，对系统动态性能的改善也没有在零极点图上进行讨论。

本文在建立系统离散状态空间模型的基础上引入了状态变量反馈，并利用闭环极点配置的方法[17]使整个系统达到最好的动态性能。同时设计了改进型观测器，在零极点图[16]上说明了闭环系统极点对观测器极点配置的影响，并通过计算推出了其限制范围。本文还讨论了LCL 参数对闭环系统极点以及状态反馈极点的影响，证明了这种使用状态观测器的状态反馈方法的鲁棒性。最后在一台10kW 的样机上验证了本文所设计的状态变量反馈以及观测器设计方法的有效性。

2 并网逆变器结构及离散状态空间模型

2.1 主电路拓扑

图1 所示为本文研究的基于LCL 滤波器的并网逆变器的主电路拓扑。其中Udc为直流侧电压，VT1～VT66 个IGBT 开关管组成三相半桥结构。Lg、Ls和C组成LCL 滤波器。其中Rg、Rs和Rc分别表示网侧电感、逆变器侧电感以及电容的等效串联电阻。

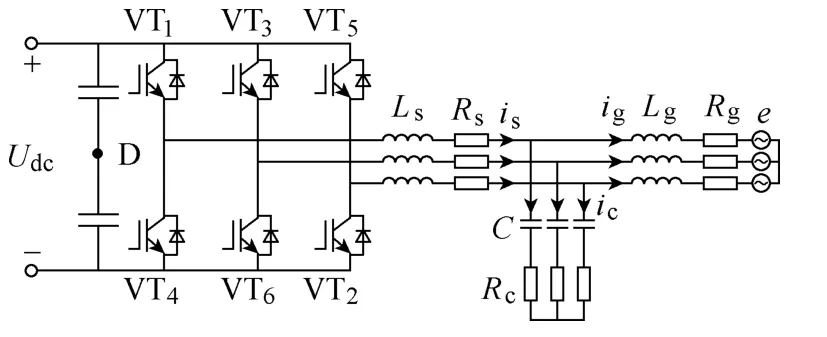
图1 基于LCL 滤波器的三相并网逆变器拓扑Fig.1 Topology of three phase grid-connected inverter with LCL-filter

2.2 传统的并网逆变器控制方式

加入状态变量反馈后的控制方式如图2 所示，主要包括两相旋转坐标系下的电流环控制以及之后的状态变量反馈。图中ssfbα和ssfbβ分别代表α 轴和β 轴的状态反馈。相对于传统的配置方法，这种反馈方式对系统的控制效果更好，能够很好地改善系统的动态响应。

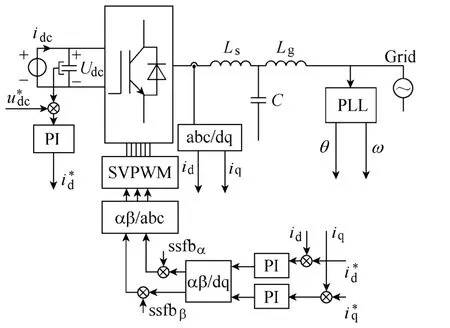
图2 并网逆变器控制策略Fig.2 Control strategy of three phase grid-connected inverter with LCL-filter

2.3 改进型离散状态空间模型

为了建立系统的状态空间方程，假设图1 中三相电网是平衡的，根据基尔霍夫电流电压定律，可以得到LCL 滤波器部分的微分方程，再通过Clarke变换，可以消除三相中的共模分量，得到两相静止坐标系下的微分方程[16]。

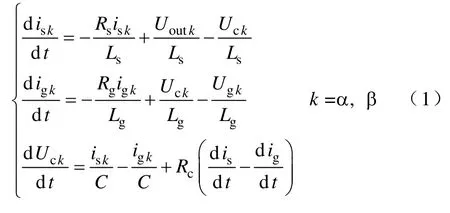
式中，isk和igk分别表示逆变器侧和网侧电流；Uoutk、Uck和Ugk分别表示逆变器输出、电容和电网电压。

由该微分方程可以得到并网逆变器LCL 滤波器部分的状态空间方程

因为并网逆变器采用离散数字控制，因此需要推导出LCL 滤波器部分的离散状态空间方程。根据连续状态空间方程和离散状态空间方程的关系，可以推出

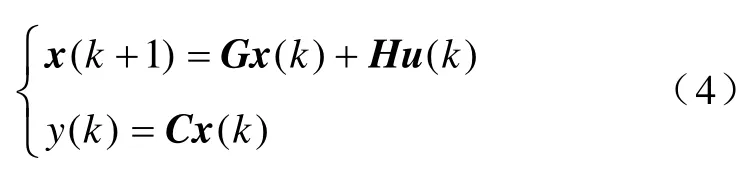
其中

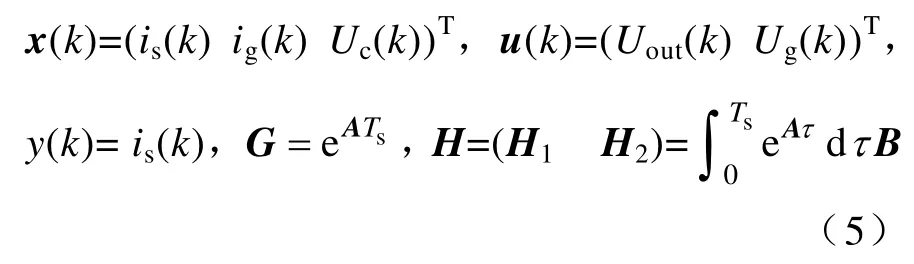
式中，Ts为离散周期。

此时系统的状态空间框图如图3 所示。

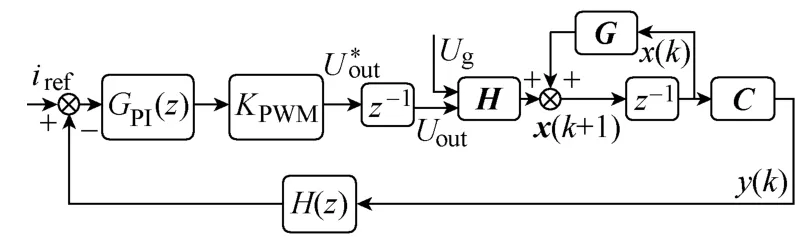
图3 系统离散状态空间模型框图Fig.3 Block diagram of discrete state space model

在实际系统中还需要考虑数字控制带来的延时。因此，需要将式（4）表示的离散状态空间方程进行改进。假设控制系统的延时为一个控制周期，则

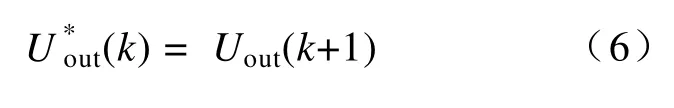
由式（6）可以将逆变器的离散状态空间方程改进为

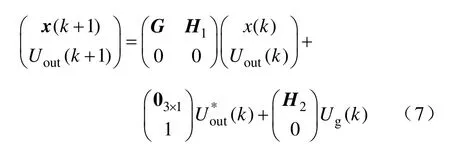
如果定义新的一组矩阵，则加入延时后系统的离散状态空间方程可以表示为

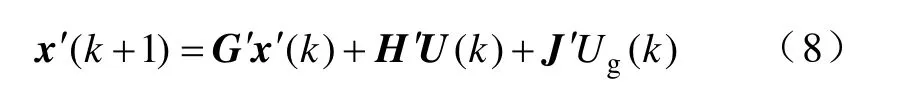
根据式（8），可以画出逆变器控制框图，如图4 所示。

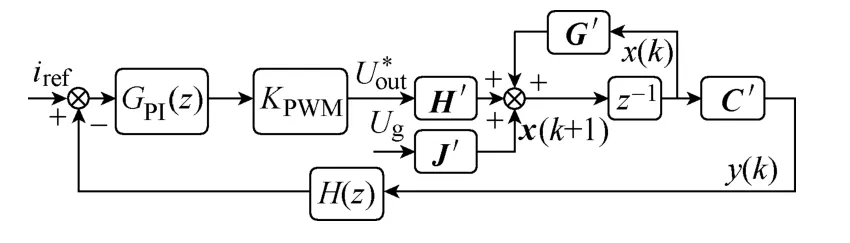
图4 改进的逆变器离散状态空间模型控制框图Fig.4 Block diagram of improved discrete state space model

3 状态变量反馈和改进型观测器的建立

3.1 状态变量反馈

在文献[22]中，已经将式（8）所表示的离散状态空间可控的充分条件归纳为

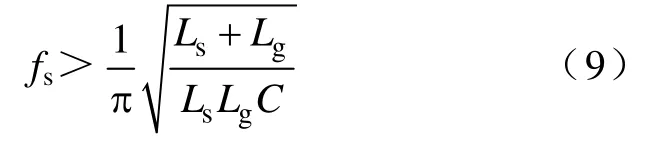
式中，fs为离散频率。

如果系统的延时与LCL 参数满足式（9），则该离散状态空间系统一定可控。这样就可以以上一小节建立的改进型离散状态空间为基础进行系统的状态变量反馈设计。加入状态变量反馈后系统控制框图如图5 所示，系统的状态空间表达式为

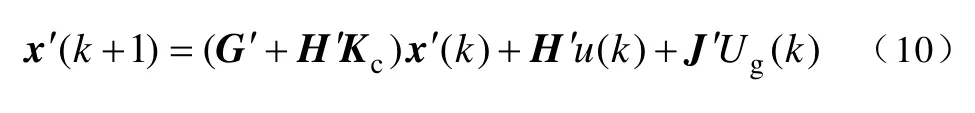
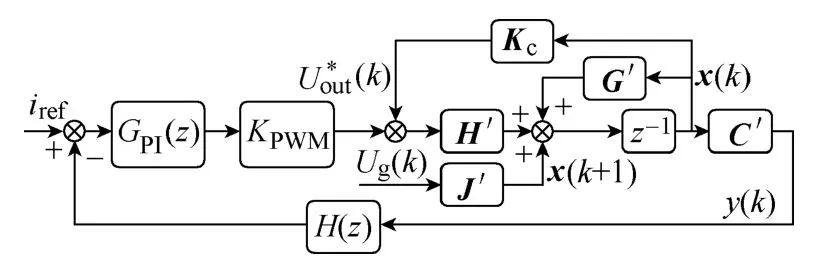
图5 加入状态变量反馈的离散状态空间模型框图Fig.5 Block diagram of discrete state space model with state variable feedback

其中，反馈矩阵定义为

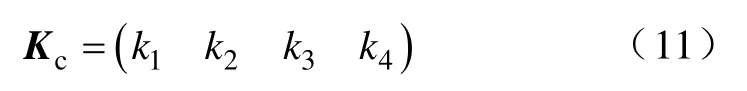
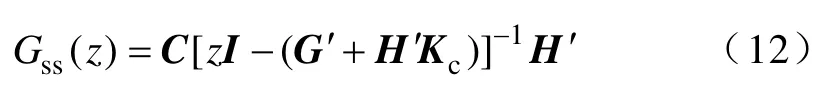
结合之前的电流环PI 调节器以及PWM 放大模块，最终可以得到系统的传递开环函数为

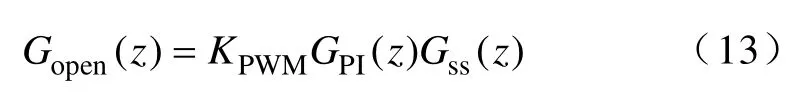
式中，GPI(z) 表示离散PI 调节器，KPWM表示PWM模块的增益。

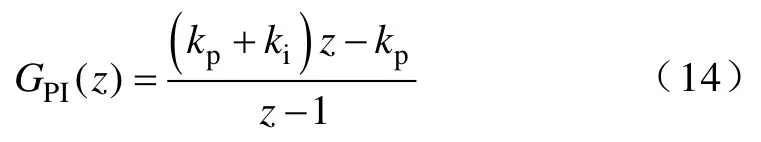
系统的闭环传递函数可以表示为

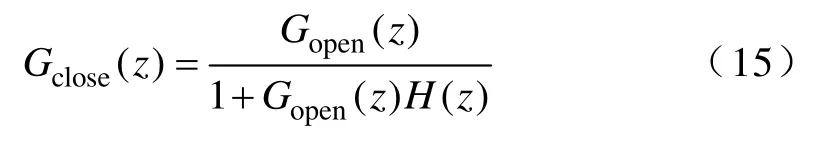
最终得到的开环离散传递函数和闭环系统离散传递函数见式（16）和式（17），其中a0～a3是与矩阵G′、H′和Kc有关的量，而b0～b2则只和矩阵G′以及H′有关；kp和ki为PI 调节器参数。

从系统的闭环传递函数可以看出该闭环系统零极点的特性。

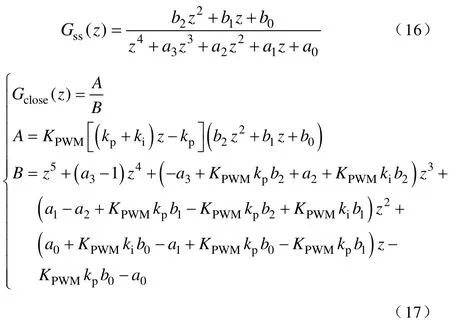
（1）这是一个五阶系统，有5 个极点和3 个零点。

（2）3 个零点中，一个零点的位置由PI 调节器参数确定，另两个零点的位置只与LCL 参数有关。

（3）5 个极点的分布与状态反馈矩阵以及PI 调节器参数有关。

（4）系统的可控参数有6 个，包括PI 调节器中的2 个参数以及状态反馈矩阵中的4 个参数。系统可调的零极点数也有6 个，包括一个零点和5 个极点。

因此，该闭环系统中的5 个极点和1 个零点完全可以通过改变状态反馈矩阵以及PI 调节器的参数来自由配置。同时另外两个零点不可改变。

3.2 改进型观测器设计

通过上述建立的改进型离散状态空间方程，可以建立Luenberger 观测器。

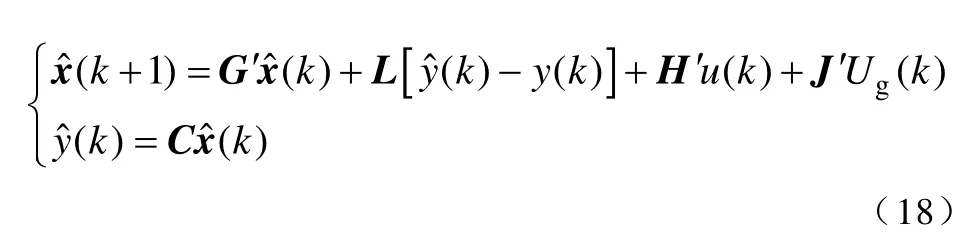
由式（18）可以得到系统的误差方程为

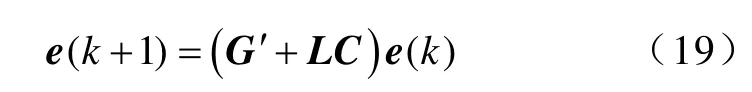
式中，L是观测器的反馈矩阵，用来让观测值更快收敛到实际值。观测器的收敛速度取决于矩阵'+G LC。

如果考虑到系统的状态变量反馈，则观测器方程应该变为

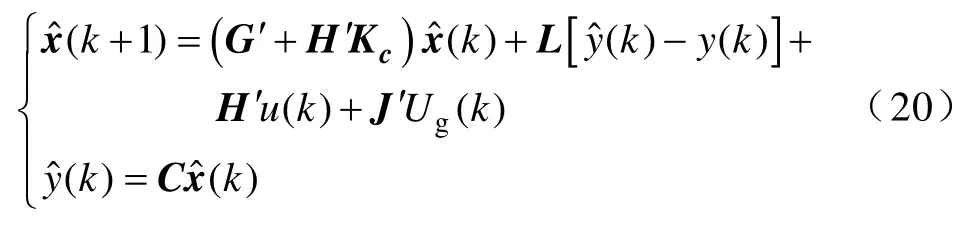
此时系统的结构框图如图6 所示。

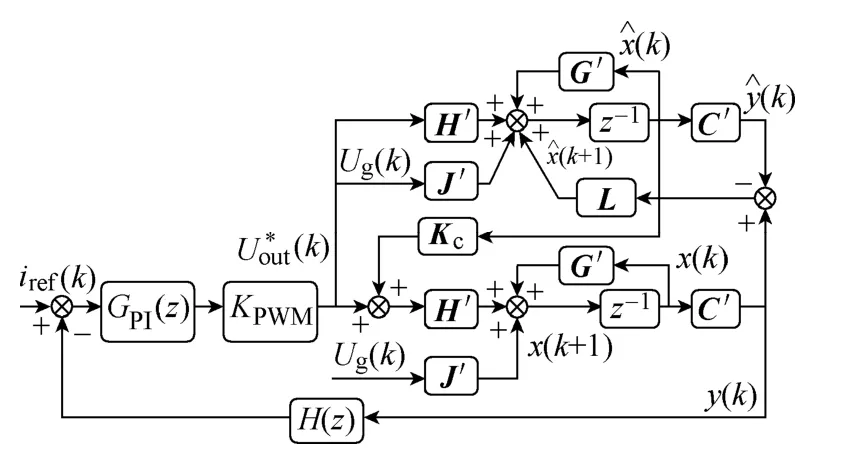
图6 加入状态观测器后系统的结构框图Fig.6 Block diagram of state space with improved state observer

状态观测器观测值的收敛速度取决于矩阵G′+H′Kc+LC。同时根据分离原则，反馈矩阵Kc以及L的配置互不影响。这对于系统的极点配置以及观测器的设计是非常有利的。

观测器的输入量是逆变器侧电流、网侧电压以及逆变器输出电压给定。因此这种观测器只需要一个逆变器侧电流传感器和一个网侧电压传感器，与传统的逆变器相同，不会增加系统的成本。

4 系统及改进型观测器极点配置

相比于传统的伯德图理论，极点配置理论更好地反映了系统的动态特性。本节就根据极点配置理论，通过配置整个系统的闭环极点来改善系统的动态特性。但由于状态变量是通过观测器得到的，因此还需要考虑到系统在引入状态观测量反馈后的稳定性。

4.1 闭环系统极点配置

上一小节已经介绍了闭环系统的零极点特性。根据极点配置理论，主导极点的阻尼设置在0.707时系统的动态效果最好。同时非主导极点对系统的作用应该尽可能小，在s平面上表示就是尽可能远离虚轴。因此，可以将系统的零极点进行如下的配置（z平面）：

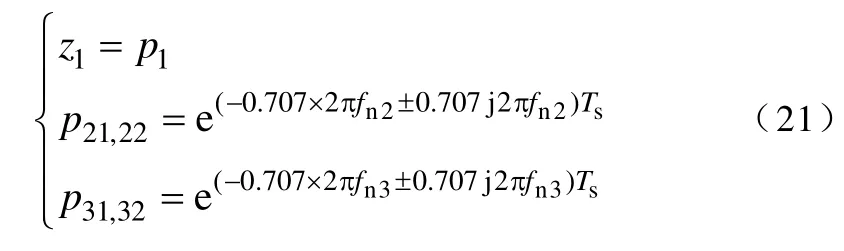
式中，fn2和fn3分别是第二对和第三对极点的振荡频率，且有fn2≪fn3。

4.2 观测器极点配置

上一小节介绍的观测器是基于状态反馈部分的模型建立的，因此观测器的极点配置要基于状态反馈部分的极点，而不是整个系统的极点。

观测器的收敛速度一般都要比所观测的系统快，因此在s域中，观测器极点的实部一般是系统极点实部的1.5～2 倍，而虚部可以保持不变。在z域中，这一关系可以表示为

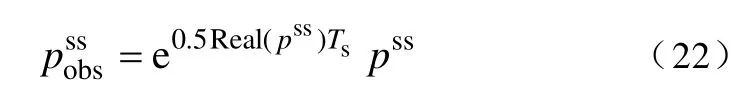
式中，上标ss 表示该极点是状态反馈部分的极点。

4.3 观测值反馈稳定性分析

实际上，当系统闭环极点的振荡频率到达一定范围以外时，状态反馈部分将处于不稳定状态（极点位于单位圆之外）。虽然从整个闭环传递函数来看系统是稳定的，但观测器只是基于状态反馈部分，因此后者的不稳定会对前者造成较大影响，特别是状态观测值还要反馈到系统中进行控制。为了保证状态观测值反馈之后系统的稳定性以及鲁棒性，有必要将状态反馈部分的极点限制在单位圆内，讨论系统闭环极点与状态反馈部分极点的关系，找到能够实现的最佳闭环系统极点配置，即在系统稳定的前提下应该尽量提高系统的响应速度，

假设状态反馈部分的离散传递函数为

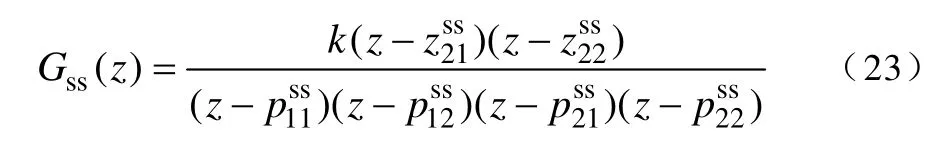
则系统的闭环传递函数可以表示为

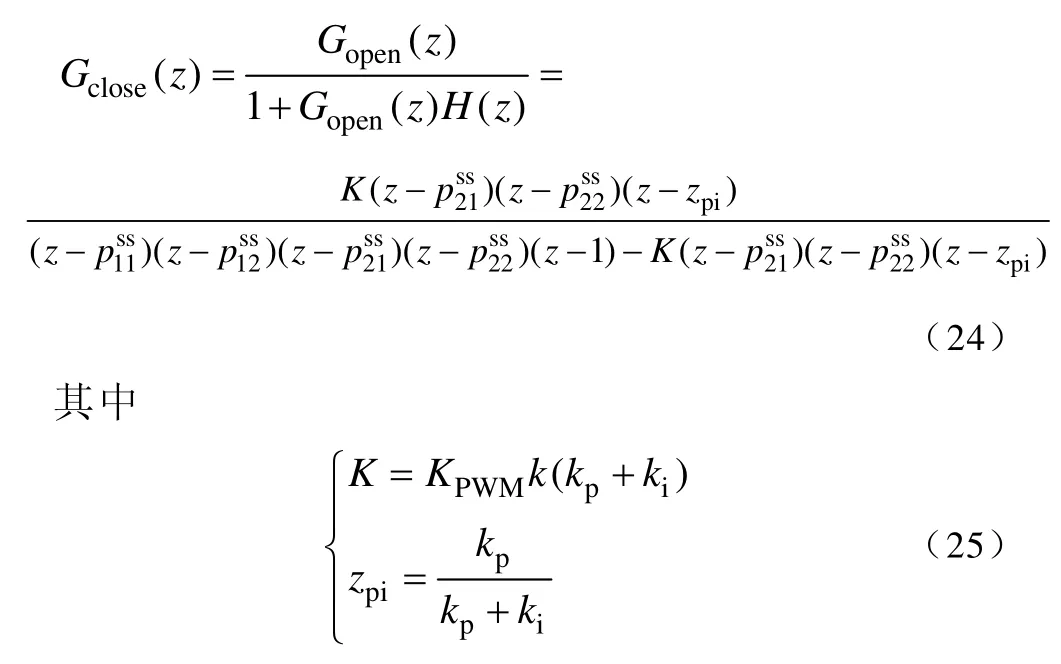
假设经过极点配置的系统闭环传递函数为

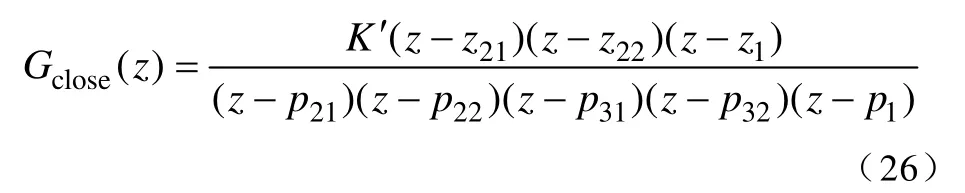
对比式（24）和式（26），再考虑到式（21）中第一个零极点的配置，不难得到

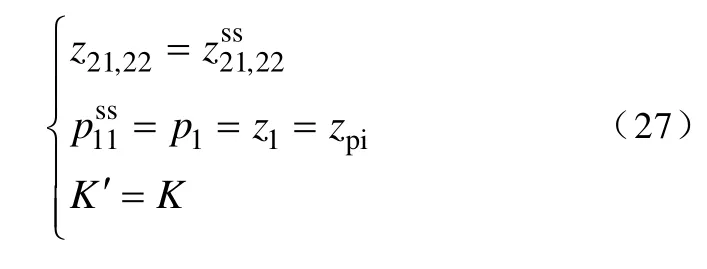
再将式（24）和式（26）的分母对应起来，即可解出状态反馈部分的极点

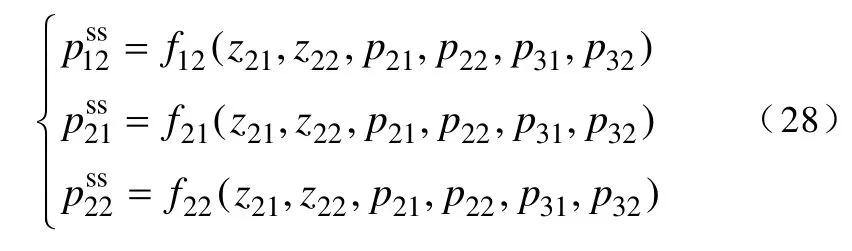
如果将式（21）的第二和第三对极点配置代入式（28），则式（28）可以化简为

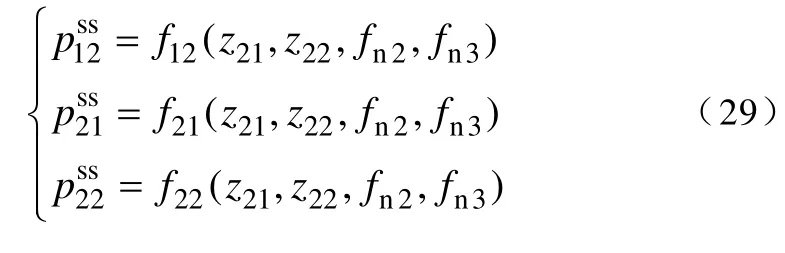
为了使状态反馈部分的极点都落在单位圆内，要求

因为零点z21和z22只与系统的LCL 滤波器参数有关，当LCL 确定时z21和z22都是常数，所以状态反馈部分的极点实际上只与闭环系统极点的振荡角频率有关，将其关系的三维图画出如图7 所示。

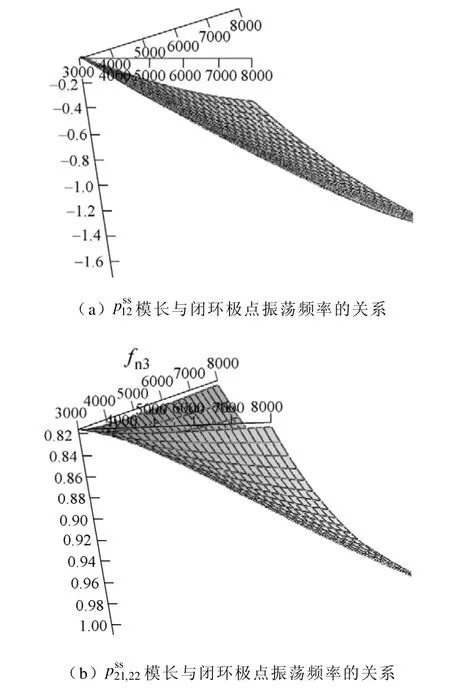
图7 状态反馈部分极点与闭环极点振荡频率的关系（z 轴位为极点到原点的模长，x、y 轴为振荡频率）Fig.7 Relationship of state space poles and the frequencies of closed-loop poles (z-axis represents the distance between poles and the original point.x,y-axis represent the frequencies of closed-loop poles respectively)

由图7 可以看出状态反馈部分极点的位置与闭环极点振荡频率的关系：当闭环极点振荡频率增大时，状态反馈部分的极点开始向单位圆外移动。

通过上述分析，可以计算出合理的闭环极点分布。如果LCL 的参数如表所示，数字运算频率选为30kHz，则系统的零极点可以配置为

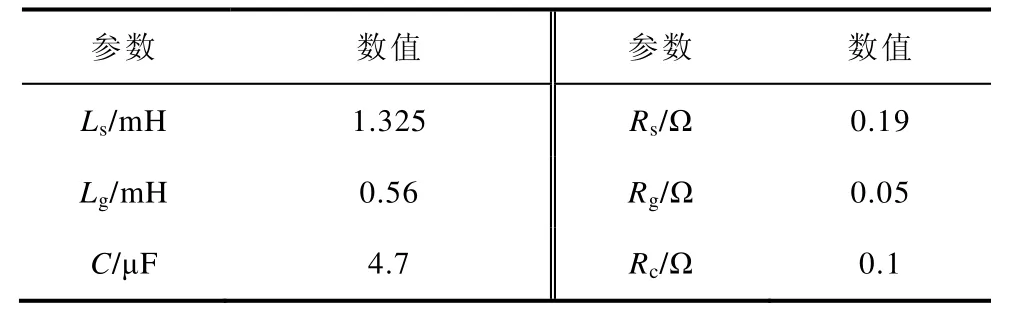
表 LCL 滤波器参数Tab.Parameters of LCL-filter

与加入状态反馈前系统（保持系统带宽不变）单位阶跃响应的对比如图8 所示。

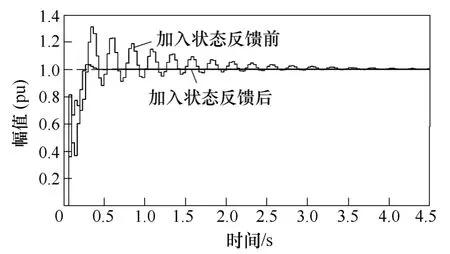
图8 加入状态反馈前和加入状态反馈后系统的阶跃响应Fig.8 Step response without and with state variables feedback

加入状态反馈后和加入状态反馈前的闭环系统根轨迹如图9a 中“×”所示，分别用虚线和实线标注。状态反馈部分的根轨迹则在图9b 中表示。其中加粗的“○”和“×”表示最终选定的零极点位置。在图9a 中可以看到经过状态反馈之后，系统的极点分布更加合理，稳定裕量更大。

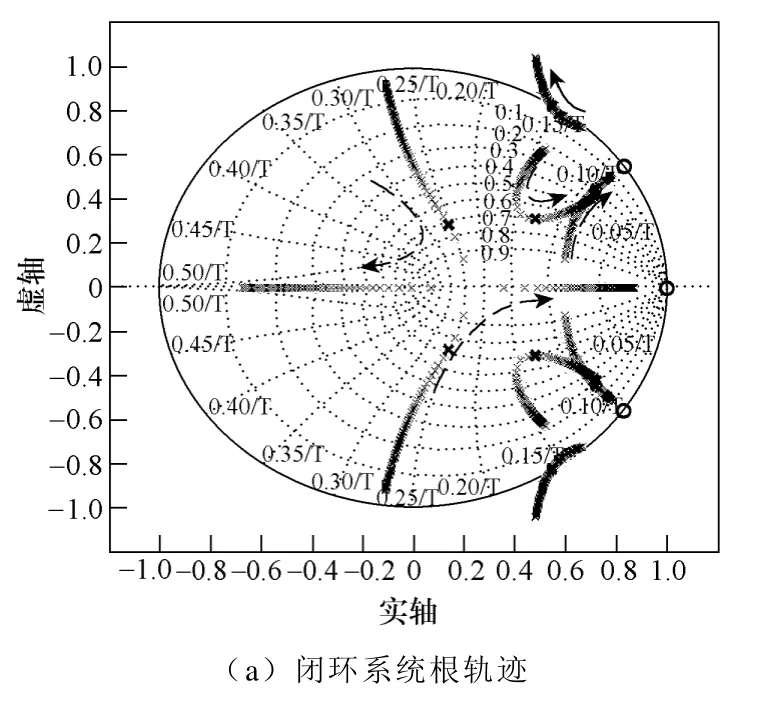
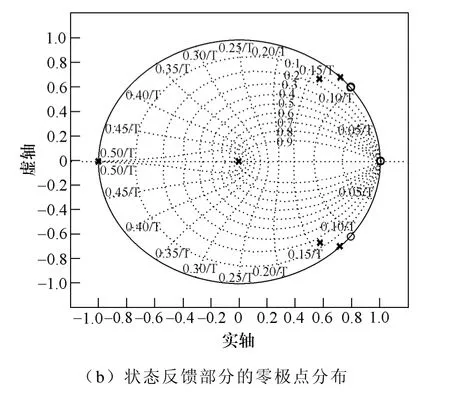
图9 系统的零极点分布Fig.9 Distribution of poles of the closed-loop system and state space

在选定系统的极点位置之后，只需要将式（15）中的分母与式（26）的分母系数一一对应列写方程，即可求出反馈矩阵Kc以及PI 调节器参数kp和ki。

确定系统极点之后，状态反馈部分的极点也随之确定，通过式（22）可以求出改进型观测器的极点配置，并得到改进型观测器反馈矩阵L，因此整个系统的设计步骤可以简述为：①建立系统的离散空间模型和改进型观测器模型；②根据LCL 参数进行最优化极点配置，确定状态反馈矩阵Kc、PI 调节器参数和观测器反馈矩阵L；③实验验证。

5 系统鲁棒性分析

5.1 系统参数对闭环极点的影响

在系统的运行中，随着功率的增大，电感会出现饱和，同时温度的变化也会导致LCL 参数发生变化，因此有必要分析系统在LCL 参数变化时的稳定性。

5.1.1Ls对系统极点的影响

当Ls从0.65～2mH 变化时，系统的根轨迹如图10a 所示。Ls对系统的影响较大，当Ls＜0.95mH 时系统会不稳定。因此实际设计中逆变器侧电感要留有足够的裕量，且要选择不易饱和的磁心。

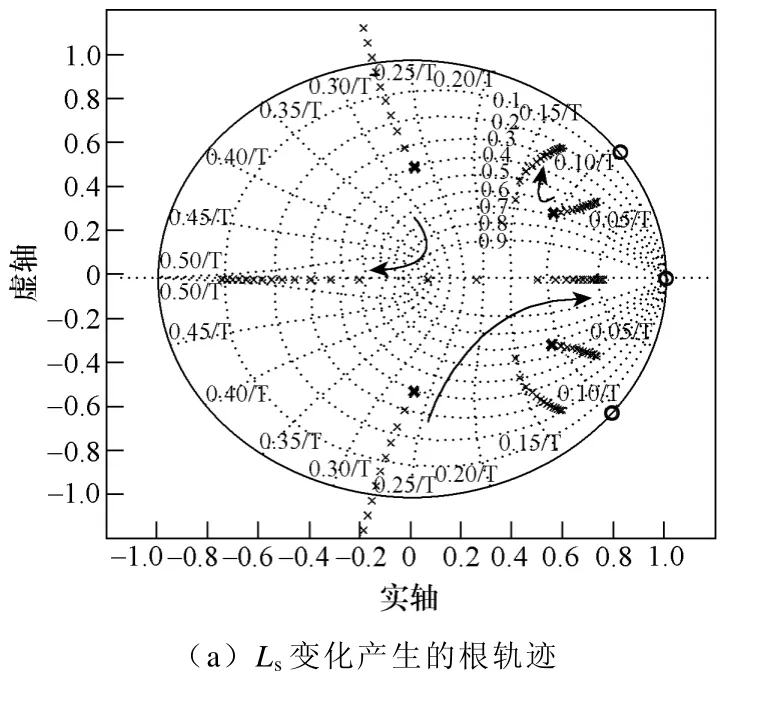
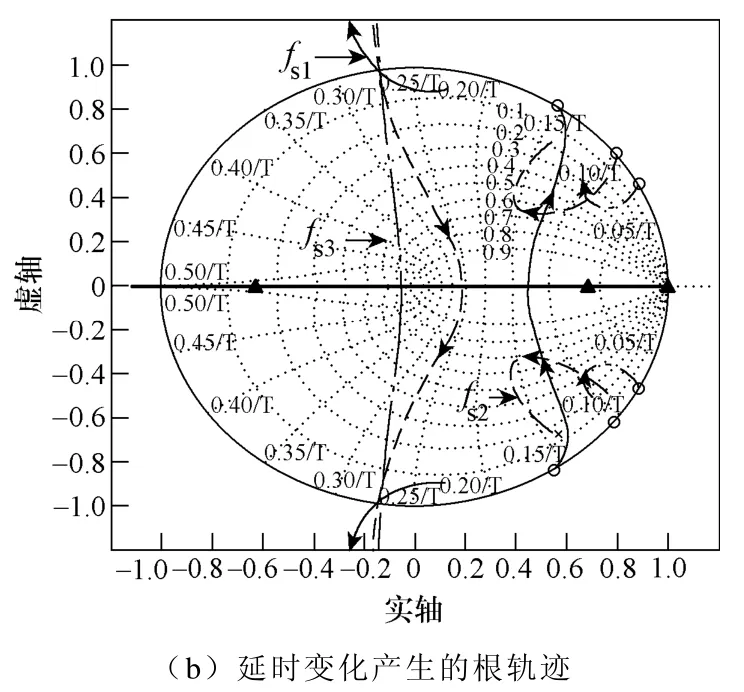
图10 系统参数变化对闭环极点位置的影响Fig.10 Influence of system parameters on the position of closed-loop poles

5.1.2Lg和C对系统极点的影响

对于Lg和C来说，系统的鲁棒性很好，在很大的范围内均稳定。但是在电容较小时，系统的阻尼不足，会使状态反馈的效果变差。

5.1.3 延时对系统极点的影响

当计算频率分别为fs1=20kHz、fs2=30kHz和fs3=40kHz 时，产生的根轨迹如图10b 所示。当计算延时大于43.5μs（23kHz）时，系统将不稳定。可见延时对系统稳定性的影响也较大。

5.2 系统参数对状态反馈部分极点的影响

5.2.1Ls对系统极点的影响

当Ls从0.65～2mH 变化时，系统的根轨迹如图11a 所示。Ls减小反而利于状态反馈部分的稳定，方便观测器的设计。

5.2.2Lg和C对系统极点的影响

对于Lg和C来说，状态反馈部分的鲁棒性很好，在很大的范围内均稳定。

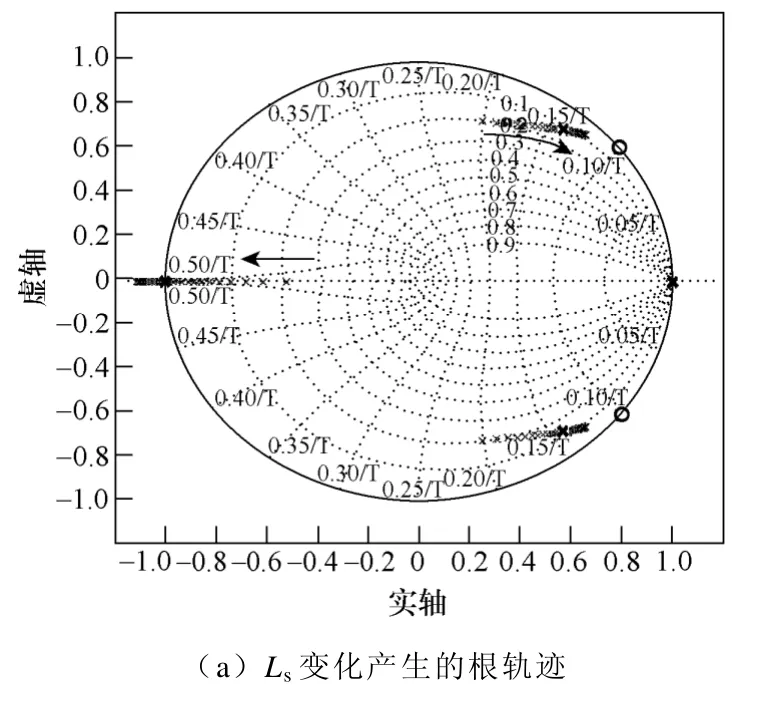
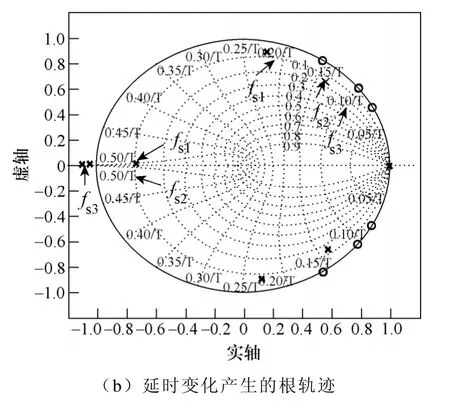
图11 系统参数变化对状态反馈部分极点的影响Fig.11 Influence of system parameters on the position of state space poles

5.2.3 延时对系统极点的影响

当计算频率分别为20kHz、30kHz和40kHz 时，产生的根轨迹如图11b 所示。当系统延时过小时反而会使状态反馈部分的极点会落在单位圆之外，此时无法设计状态观测器。

通过上述分析可以发现，相对于闭环系统，状态反馈部分鲁棒性更好，这也证明了状态观测器的鲁棒性——系统参数发生变化时也能保持稳定。

6 实验验证

为了验证上述状态反馈以及状态观测器设计的有效性，根据图1和图2 的拓扑以及控制原理，搭建了一个10kW 的基于LCL 滤波器的并网逆变器实验平台。LCL 滤波器的参数如前表所示。所有的控制算法，包括直流电压外环、状态变量反馈、电流PI 内环以及改进型状态观测器都在德州仪器微控制器TMS320F28335 中实现。系统的载波频率为15kHz，计算频率为30kHz。采用SVPWM 控制方式。逆变器交流侧直接与电网相连，直流母线电压设定为650V。实验结果显示改进型观测器能够很好地对系统的状态变量进行观测，同时经过状态反馈，系统的动态性能有显著的提升，稳态性能也有一定的改善。

观测器的观测效果通过数字到模拟转换（Digital Analog Conversion,DAC）后输出到示波器进行观测。图12a 所示为改进型观测器的网侧电流观测效果。图12b 则为电容电压的观测效果。图13是在电流给定从半载突变为1/4 载时观测器的动态跟踪效果。

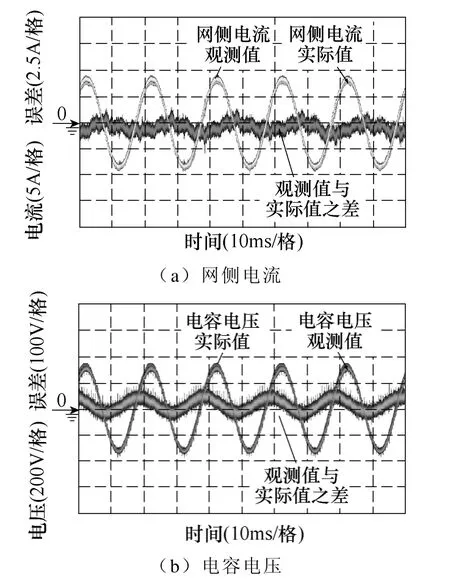
图12 改进型状态观测器稳态观测效果Fig.12 Steady state performance of the improved state observer

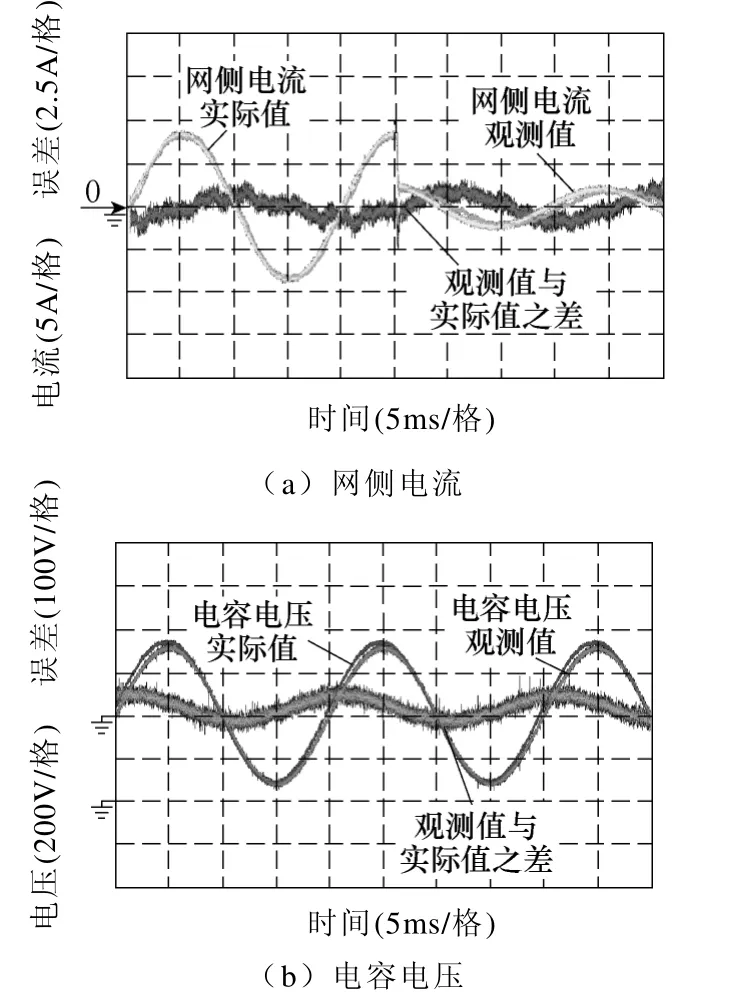
图13 改进型状态观测器动态观测效果Fig.13 Dynamic performance of the improved state observer

改进型观测器与传统观测器的观测效果对比如图14 所示。在相同极点配置下，改进型观测器在观测效果上要明显优于传统观测器，网侧电流观测误差最大值从5A 降到了1.5A。可见系统延时对观测器影响很大。

将观测器观测得到的观测值用于状态变量反馈，得到的系统稳态波形图如图15 所示。图16是系统在使用状态变量反馈后的动态响应。

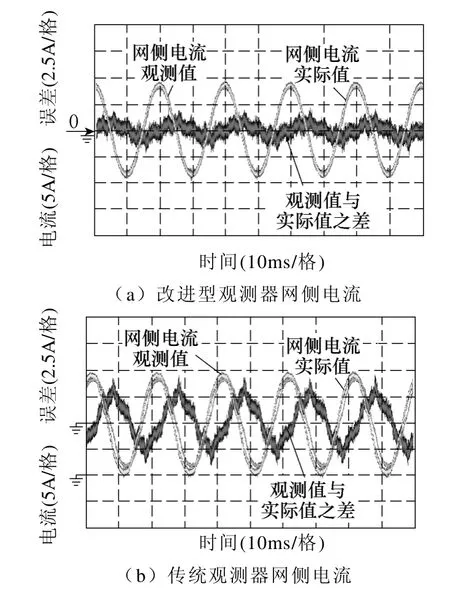
图14 改进型观测器与传统观测器观测效果对比Fig.14 Comparison between improved state observer and traditional state observer

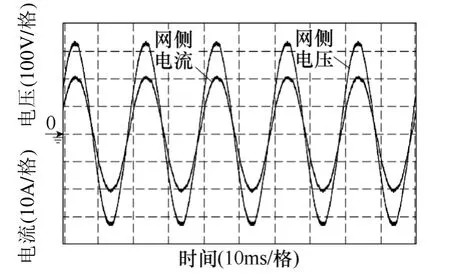
图15 加入状态变量反馈后网侧电压和电流稳态波形Fig.15 Steady state performance of grid voltage and current with state variable feedback

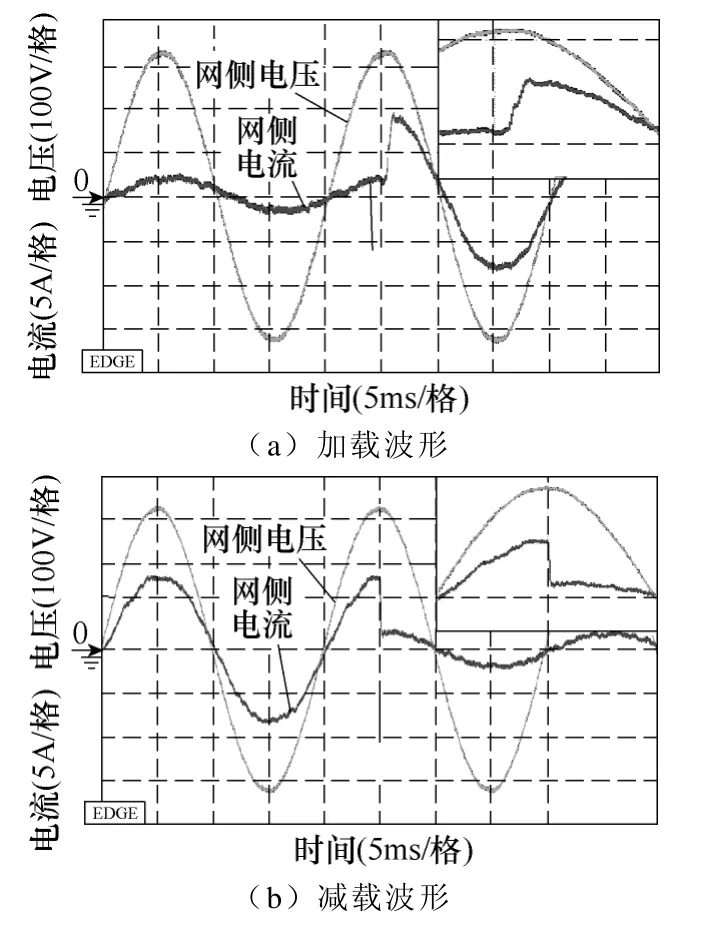
图16 加入状态反馈后网侧电压电流的动态响应波形Fig.16 Dynamic performance of grid voltage and current with state variable feedback

图17 所示为不加状态反馈时的动态响应波形。如果与不加状态反馈的系统进行比较可以发现，在加入状态反馈之后，系统的动态性能得到了极大的改善。在减载时，电流超调量明显减少，同时系统很快进入稳态，而几乎不产生任何振荡，调整时间减小。而在加载时则没有任何振荡。再比较d 轴电流的动态波形，如图18 所示。

图17 不加状态反馈时网侧电压电流的动态响应波形Fig.17 Dynamic performance of grid voltage and current without state variable feedback

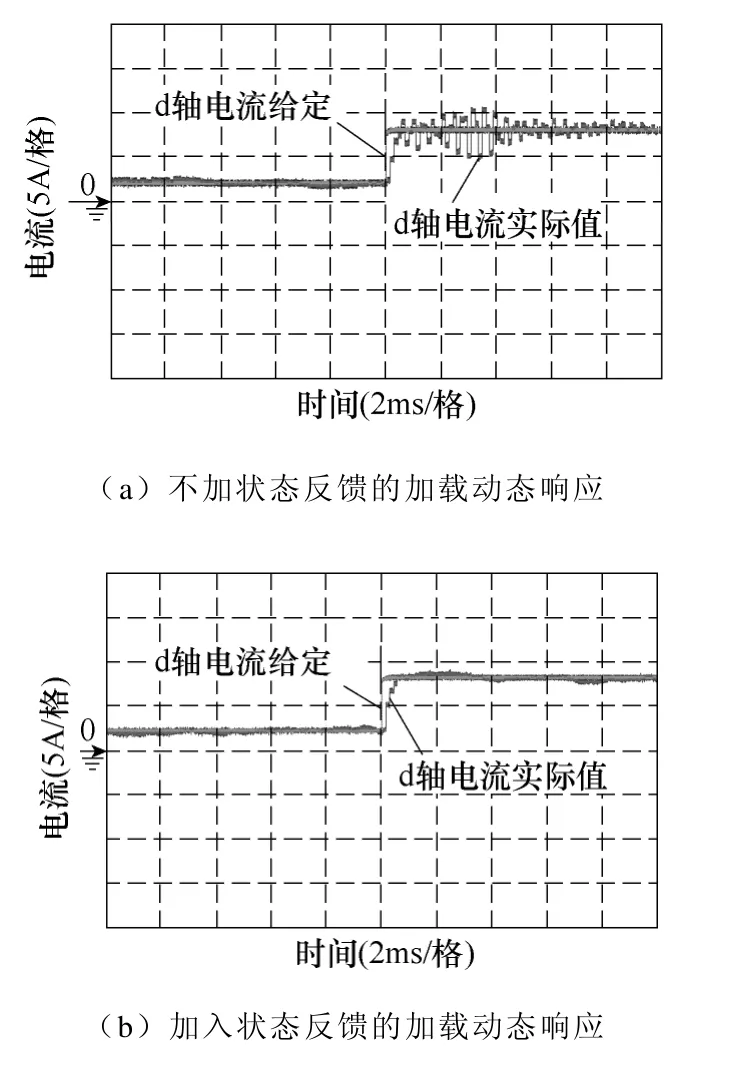
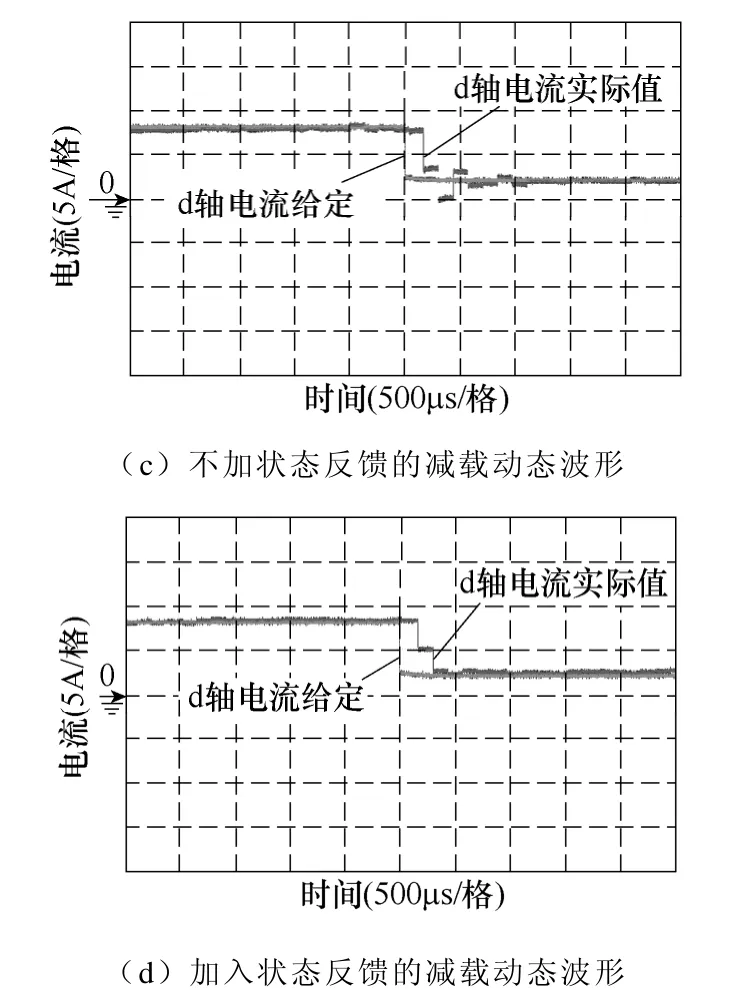
图18 d 轴电流阶跃响应对比Fig.18 Comparison of the current step response under d axis

由于DAC 的传输速率有限，图中观测值呈现阶梯状，但结果仍能够说明问题。

经过分析得到，在加入状态反馈之前，d 轴电流分量从半载到1/4 载的调整时间为1ms，超调量为2A。此时系统带宽已经接近临界稳定，1/4 载到半载时有可能产生振荡（见图17a），且满载时不稳定（电流增大造成电感值减小）；而在加入状态反馈之后并网电流的调整时间降低为300μs，超调量则接近零，且满载工作也非常稳定。

将PI 参数调节到全负载范围稳定，对比状态反馈方法和普通PI 调节方法的稳态波形，可以得到如图19 所示的THD 分布。

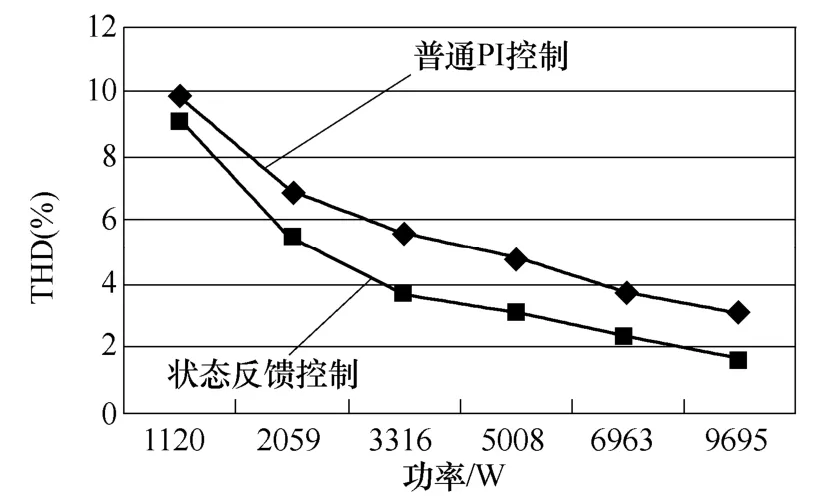
图19 不同功率下并网电流THD 对比Fig.19 Comparison of grid current THD under different loads

通过以上实验，可以证明基于状态观测器的状态反馈对系统的动态以及稳态都有改善效果。

7 结论

本文在建立改进型离散状态空间方程的基础上，通过闭环极点配置实现了系统的最佳阻尼，明显改善了系统的动态响应。设计了基于改进型离散状态空间方程的改进型状态观测器，避免系统传感器数量的增加。同时还讨论了闭环极点对状态观测器极点配置的影响、状态观测值反馈的稳定范围以及系统参数变化对稳定性的影响。最后在10kW 并网逆变器样机上证实了所提出的方案对系统动态和稳态效果的改善。

[1]张强,张崇巍,张兴,等.风力发电用大功率并网逆变器研究[J].中国电机工程学报,2007,27(16):54-59.Zhang Qiang,Zhang Chongwei,Zhang Xing,et al.Study on grid-connected inverter used in high-power wind generation system[J].Proceedings of the CSEE,2007,27(16):54-59.

[2]戴欣平,马广,杨晓红.太阳能发电变频器驱动系统的最大功率追踪控制法[J].中国电机工程学报,2005,25(8):95-99.Dai Xinping,Ma Guang,Yang Xiaohong.A control method for maximum power tracing of photovoltaic generation system[J].Proceedings of the CSEE,2005,25(8):95-99.

[3]姚志垒,王赞,肖岚,等.一种新的逆变器并网控制策略的研究[J].中国电机工程学报,2006,26(18):61-64.Yao Zhilei,Wang Zan,Xiao Lan,et al.Research on a novel grid-connected control strategy of inverter[J].Proceedings of the CSEE,2006,26(18):61-64.

[4]Liserre M,Blaabjerg F,Hansen S.Design and control of an LCL-filter-based three-phase active rectifier[J].IEEE Transactions on Industry Applications,2005,41(5):1281-1291.

[5]王斯然,吕征宇.LCL 型并网逆变器中重复控制方法研究[J].中国电机工程学报,2010,30(27):69-75.Wang Siran,Lü Zhengyu.Research on repetitive control method applied to grid-connected inverter with LCL filter[J].Proceedings of the CSEE,2010,30(27):69-75.

[6]徐志英,许爱国,谢少军.采用LCL 滤波器的并网逆变器双闭环入网电流控制技术[J].中国电机工程学报,2009,29(27):36-41.Xu Zhiying,Xu Aiguo,Xie Shaojun.Dual-loop grid current control technique for grid-connected inverter using a LCL filter [J].Proceedings of the CSEE,2009,29(27):36-41.

[7]Routimo M,Tuusa H.LCL type supply filter for active power filter-comparison of an active and a passive method for resonance damping[C].IEEE Power Electronics Specialists Conference,2007:2939-2945.

[8]Liserre M,Dell'Aquila A,Blaabjerg F.Stability improvements of an LCL-filter based three-phase active rectifier[C].IEEE 33rd Annual Power Electronics Specialists Conference,2002:1195-1201.

[9]Malinowski M,Bernet S.A simple voltage sensorless active damping scheme for three-phase PWM converters with an LCL filter[J].IEEE Transactions on Industrial Electronics,2008,55(4):1876-1880.

[10]Siran Wang,Xia Zhou,Jifeng Chen,et al.Investigation of fully digital controlled Li-ion battery power recovery system[C].IEEE Applied Power Electronics Conference and Exposition,Twenty-Fifth Annual,2010:2091-2095.

[11]Poh Chiang Loh,Holmes D G.Analysis of multiloop control strategies for LC/CL/LCL-filtered voltagesource and current-source inverters[J].IEEE Transactions on Industry Applications,2005,41(2):644-654.

[12]Erika Twining,Holmes D G.Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J].IEEE Transactions on Power Electronics,2003,18(3):888-895.

[13]Wessels C,Dannehl J,Fuchs F W.Active damping of LCL-filter resonance based on virtual resistor for PWM rectifiers stability analysis with different filter parameters[C].IEEE Power Electronics Specialists Conference,2008:3532-3538.

[14]Shen Guoqiao,Xu Dehong,Cao Luping,et al.An improved control strategy for grid-connected voltage source inverters with an LCL filter[J].IEEE Transactions on Power Electronics,2008,23(4):1899-1906.

[15]Shen Guoqiao,Zhu Xuancai,Zhang Jun,et al.A new feedback method for PR current control of LCLfilter-based grid-connected inverter[J].IEEE Transactions on Industrial Electronics,2010,57(6):2033-2041.

[16]Eric Wu,Lehn P W.Digital current control of a voltage source converter with active damping of LCL resonance[J].IEEE Transactions on Power Electronics,2006,21(5):1364-1373.

[17]Dannehl J,Fuchs F W,Th X F,et al.PI state space current control of grid-connected pwm converters with LCL filters[J].IEEE Transactions on Power Electronics,2010,25(9):2320-2330.

[18]Ogata Katsuhiko[美].离散时间控制系统.陈杰等译[M].北京:机械工业出版社,2005.

[19]Xue Mingyu,Zhang Yu,Liu Fangrui,et al.Optimized pole and zero placement with state observer for LCL-type grid-connected inverter[C].IEEE Energy Conversion Congress and Exposition,2011:377-382.

[20]Choi C H.Step response improvement by pole placement with observer[C].40th Southeastern Symposium on System Theory,2008:7-12.

[21]侯朝勇,胡学浩,惠东.基于离散状态空间模型的LCL 滤波并网变换器控制策略[J].中国电机工程学报,2011,31(36):8-15.Hou Chaoyong,Hu Xuehao,Hui Dong.Control strategy of grid-connected converter with LCL filter based on discrete state-space model[J].Proceedings of the CSEE,2011,31(36):8-15.

[22]Gabe I J,Montagner V F,Pinheiro H.Design and implementation of a robust current controller for VSI connected to the grid through an LCL filter[J].IEEE Transactions on Power Electronics,2009,24(6):1444-1452.