并联逆变器输出阻抗分析及电压控制策略

张庆海 罗 安 陈燕东 彭楚武 彭自强

（1.湖南大学电气与信息工程学院 长沙 410082 2.国网山东省电力公司聊城供电公司 聊城 252000）

1 引言

为了更好地挖掘分布式发电的潜力，解决分布式发电对大电网带来的不利影响，采用微电网的形式接纳分布式电源，已成为当前电力系统研究的热点[1,2]。近几年来，随着许多实验性质微电网的运行，在微电网能量管理系统和电力电子接口控制等方面已取得了一定的成果[3-5]，但由于实际中的小容量分布式电源大量存在，使得低电压微电网日益成为研究热点[6-10]。

低电压微电网在孤岛运行时的关键难点问题是多逆变器的并联运行。在无互联线的逆变器并联中，通过选取不同的并联逆变器控制方式，可以改变逆变器的输出阻抗特性。无互联线的逆变器并联大多采用下垂控制方法[11]，传统的下垂控制方法一般将逆变器的输出阻抗设计成电感性[12]。然而，低电压微电网中，低压线路的线路电阻远大于线路感抗，在这种条件下应用传统下垂控制法，容易导致系统功率分担的精确性变差，系统稳定性变弱，逆变器间环流较大[13,14]。

针对低电压微电网的上述特性，国内外相继提出了许多改进下垂控制法。文献[13]提出了基于虚拟功率的下垂控制法，通过把实际有功功率和无功功率分别转换成虚拟功率，对传统下垂控制法进行修正。对此，文献[14]指出，虚拟功率作为直接控制变量，并不能保证实际有功功率和无功功率在各个分布式电源之间的精确分配，进而提出了基于虚拟频率-电压的下垂控制法，然而其控制算法较为复杂，难以在工程应用中实现。

另一方面，逆变器控制环中引入虚拟阻抗[8-10]，可有效地改变逆变器输出阻抗幅频特性。根据输出阻抗在工频条件下的幅频特性，然后采取相应的下垂控制方法计算并合成参考电压。本文即采取此种方案进行分析。

本文以线路电阻较大的低电压微电网为研究对象，首先从并联逆变器的电压控制方式入手，通过引入虚拟复阻抗，将逆变器的输出阻抗在工频条件下设计呈电阻性；通过幅频特性分析，详细地探讨了不同控制参数对于输出阻抗的影响，选取了合适的控制参数，给出了相应的下垂控制方法。以上基于虚拟复阻抗的电压控制策略，适用于低电压微电网多逆变器并联控制，能够有效提高系统功率分担的精确性和系统稳定性。

2 多逆变器并联系统

图1 所示为本文提出的多逆变器并联系统结构示意图。Udc为分布式电源输出直流电压，S1～S4构成单相全桥逆变主电路,D为功率器件的开关状态控制变量，uinv为一个开关周期内逆变器输出电压的平均值。逆变器输出电压通过电感L和电容C构成LC 滤波器滤除高频毛刺，由低压线路连接到输出交流负载上。io为线路电流，滤波电感的等效电阻值设为rL，iL为电感电流，iC为电容电流，vo为滤波电容电压，φ为合成参考电压的初始相位角。

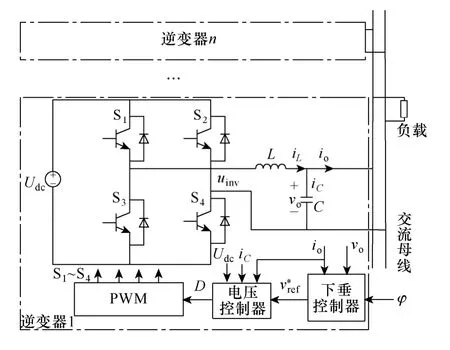
图1 多逆变器并联系统结构示意图Fig.1 Schematic diagram for parallel multi-inverters system

逆变器控制采取基于虚拟复阻抗的电压控制策略，具体实施方案为:下垂控制器计算合成参考电压，电压控制器对参考电压进行跟踪控制。

由图1，当开关周期足够短时，用各交流变量的瞬时值替代其一个开关周期内的平均值，则有如下两式成立。

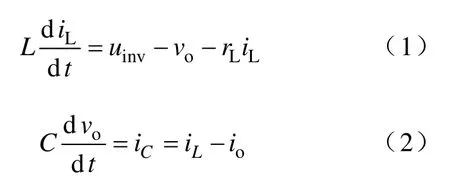
联立以上等式，得

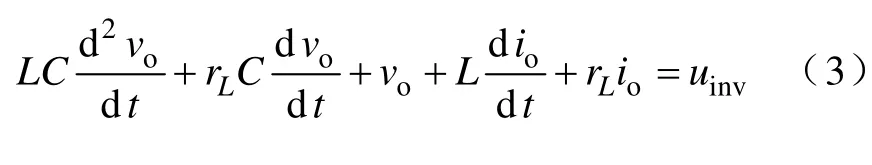
输出阻抗的幅频特性不同，采用的下垂控制方法也就不同。本文首先进行逆变器输出阻抗设计与分析，然后提出一种基于虚拟复阻抗的电压控制策略，设计下垂控制器计算合成参考电压。

3 输出阻抗设计

采用PID 控制跟踪逆变器输出电压，如下所示。

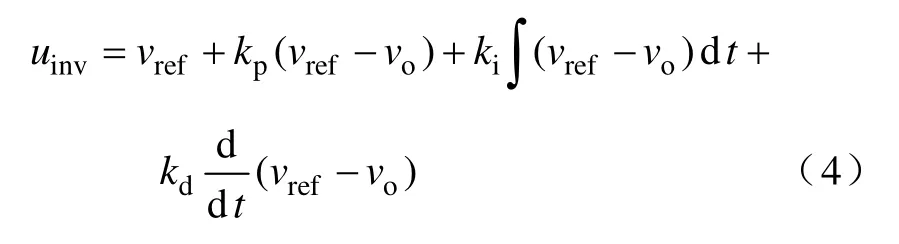
式中，仍用一个开关周期中各交流变量的瞬时值代替其平均值。其中，vref为参考电压。

联立式（3）和式（4），有

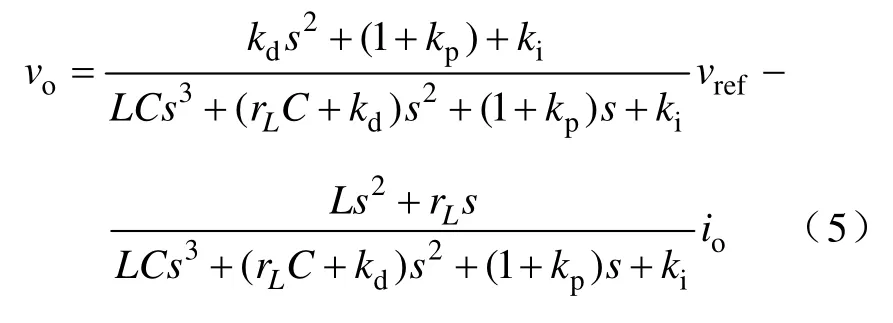
上式可进一步写成

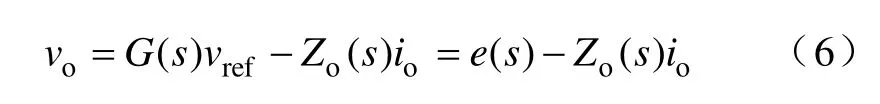
式中，G(s)为电压增益；e(s)为空载输出电压；Zo(s)为逆变器输出阻抗。

由于滤波电感的影响，一般情况下逆变器输出阻抗呈电感性，传统下垂控制法即基于此。然而，在应用下垂控制方法于逆变器并联控制时，单个逆变器的整体阻抗应为逆变器输出阻抗与线路阻抗之和。当逆变器输出阻抗与线路阻抗之和并非呈现明显的电感性时，传统下垂控制策略就不适用。

低电压微电网中线路阻抗比的值远高于中压或高压线路，线路越长，线路电阻值越高[15]。所以，如能使得工频条件下逆变器的输出阻抗为电阻性，则逆变器输出阻抗和线路阻抗之和可呈现较大的电阻性且感性分量很小可忽略不计。由此，利用电阻性条件下的下垂控制方法，可解决传统下垂控制法在低电压微电网中应用时，由于线路电阻值相对较高而可能引起的系统稳定性较差、功率分担精确性较低等不足。

为改变逆变器输出阻抗特性，本文引入虚拟复阻抗

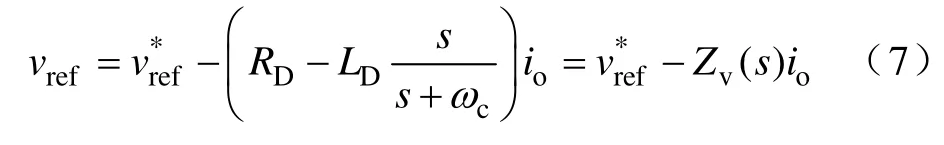
式中，ωc为低通滤波器的截止频率，加入低通滤波器后，可以有效地避免高频噪声干扰。RD为虚拟电阻，LD为虚拟电感。考虑降低逆变器的输出感抗值，虚拟感抗取负值，即Zv(s) 实际呈阻容性。

引入式（7）虚拟阻抗的参考电压示意图如图2所示。这时，逆变器输出阻抗值变为

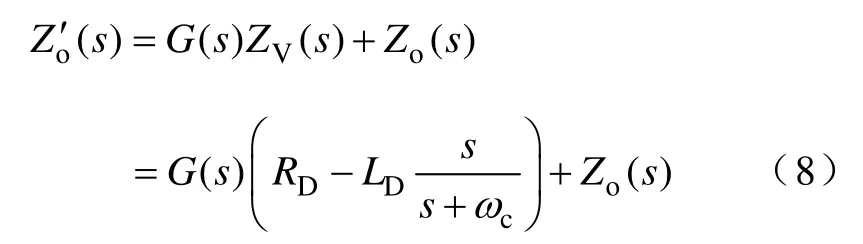
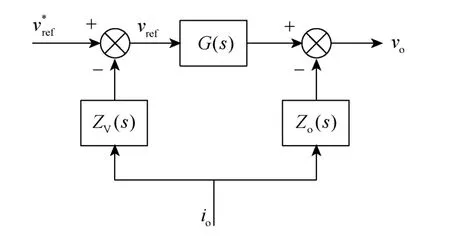
图2 参考电压引入虚拟复阻抗示意图Fig.2 Diagram of reference voltage with virtual complex impedance

将式（5）和式（6）中G(s) 和Zo(s)的值代入式（8），结果如式（9）所示。

4 引入虚拟复阻抗的逆变器输出阻抗分析

未引入虚拟复阻抗时逆变器输出阻抗Zo(s) 和改进后输出阻抗(s) 幅频特性如图3 所示。其仿真参数见表1 所示。

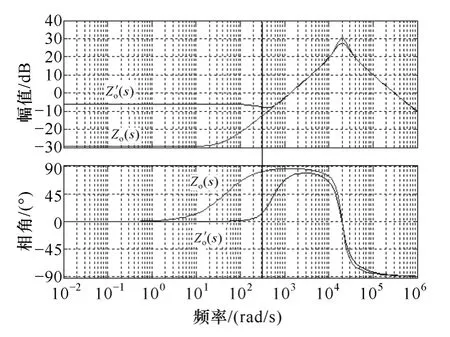
图3 Zo(s) 和(s) 幅频特性Fig.3 Bode diagrams of the output impedance Zo(s)and (s)

表1 Zo(s) 和(s) 仿真参数Tab.1 Simulation parameters of Zo(s) and (s)

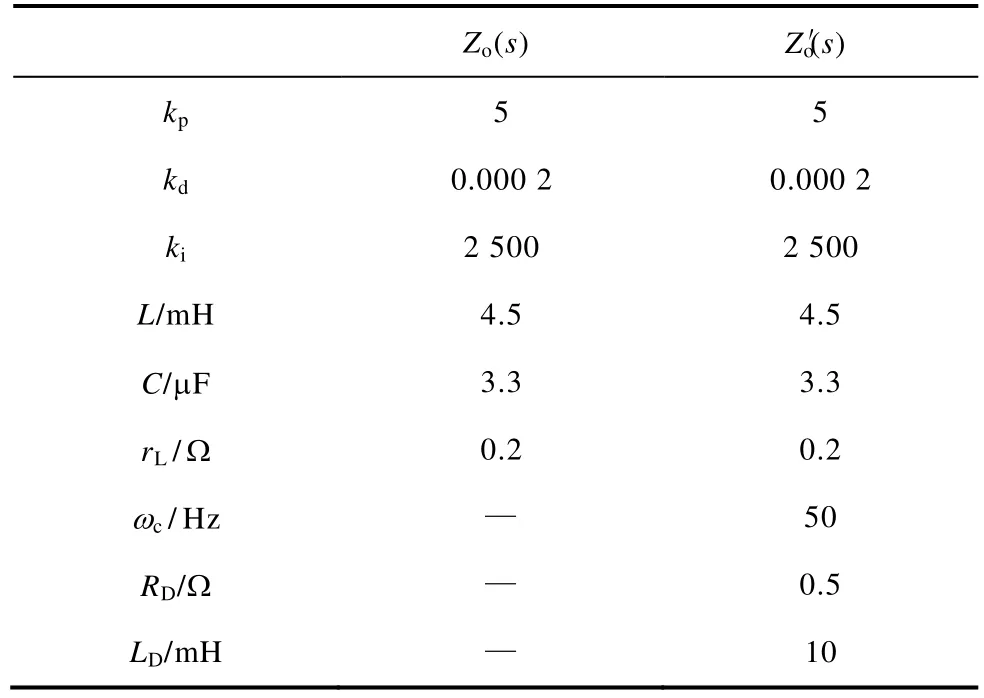
表1 Zo(s) 和(s) 仿真参数Tab.1 Simulation parameters of Zo(s) and (s)

可见，引入式（8）所示虚拟复阻抗后，逆变器输出阻抗在工频条件下呈电阻性，幅值在低频条件下可基本保持恒定。但未加入虚拟阻抗时，输出阻抗在工频条件下呈电感性且其幅值对频率变化极其敏感。

观察输出阻抗在低频条件下的幅值还可以看出，Zo(s) 的幅值很小，加入虚拟复阻抗后，通过增大式（8）中RD的取值，Zo'(s) 中电阻分量明显增加，(s)在低频条件下的幅值也明显增大。

下面进一步探讨参数kd、ki和RD对(s) 的影响，为便于比较，以表1 中所示(s) 的参数为基准，分别设定kd=0、ki=5 000、RD=1.5，其余参数不变，则输出阻抗(s) 的幅频特性图如图4 所示。

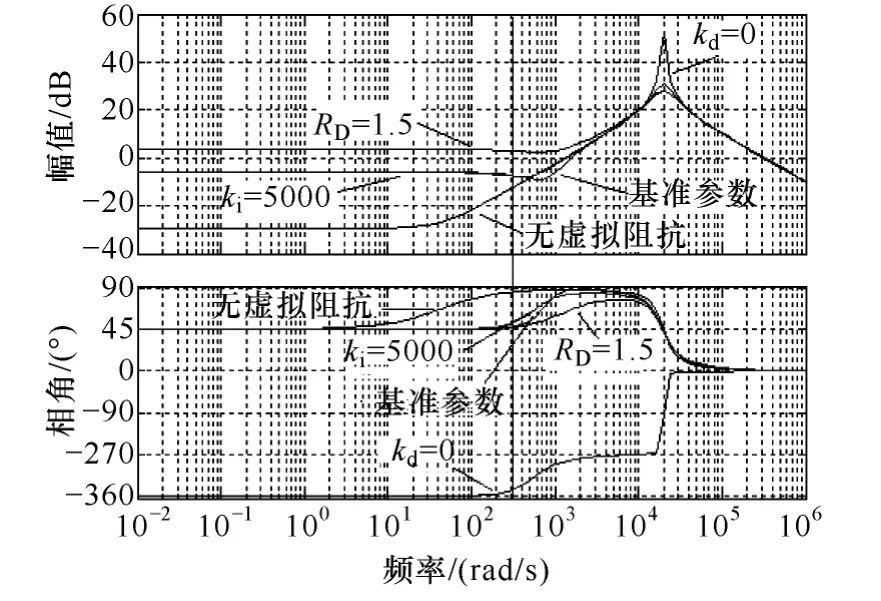
图4 不同参数条件下输出阻抗幅频特性图Fig.4 Bode diagrams of the output impedance with different parameters

由图4 可见，式（4）中微分环节(即kd值)的变化，影响高频条件下输出阻抗的特性；ki=5 000 和RD=1.5 时，输出阻抗的频率特性相对基准参数条件下要好。但对RD的取值而言，进一步的仿真分析可发现，并非越大越好，RD变大引起逆变器输出阻抗幅值变大。如图4 中，RD取值为1.5 时，输出阻抗相对RD=0.5 时增大。文献[16]详细分析了逆变器输出阻抗大小对并联系统均流的影响，并指出:较大的输出阻抗虽然能够取得较好的功率均分效果，但应用下垂控制法时，逆变器空载输出电压相对空载输出电压参考值亦产生较大的电压降。因此，对式（7）而言，为使得逆变器输出阻抗呈电阻性而在虚拟阻抗中引入过大的虚拟电阻RD是不可取的。

为了体现式（7）与单一引入虚拟电阻的不同，仍以表2 中所示(s) 数据为基准参数，令虚拟电感LD分别取值为100mH、200mH，按照式（9）计算得到的输出阻抗的幅频变化如图5 中所示，箭头所示方向为LD取值依次变大引起的幅值和频率变化趋势。可见，当RD取一定值时，LD的值在一定范围内变化，可使输出阻抗更加接近纯电阻性。

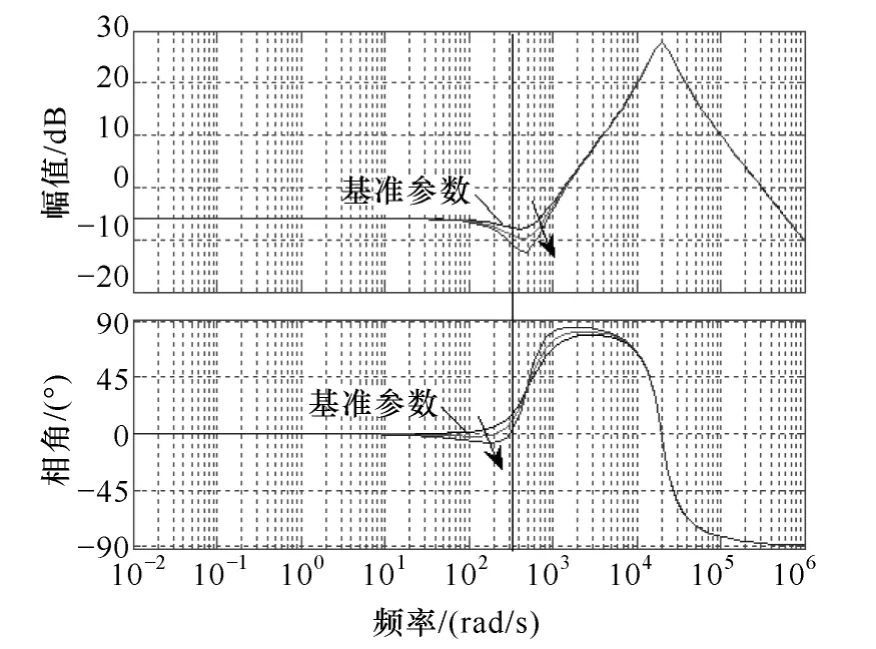
图5 不同虚拟电感值条件下输出阻抗幅频特性图Fig.5 Bode diagrams of the output impedance with different virtual inductance values

综上所述，引入式（7）所示的虚拟复阻抗，虚拟阻抗中同时包含虚拟电阻和虚拟感抗，虚拟电阻可增大逆变器输出电阻值；而虚拟感抗为负值，呈电容性，可降低逆变器输出阻抗中固有的感性分量，从而使逆变器输出阻抗在工频下呈纯阻性。

5 电压控制策略

5.1 基于虚拟复阻抗的电压控制策略

图6 所示为提出的基于虚拟复阻抗的电压控制框图，脉宽调制环节等效为一个放大倍数正比于直流电压Udc的比例放大增益kPWM。需要指出的是，式（4）中微分环节的存在对控制器的计算精度提出了较高的要求，因而，尽量避免微分运算，可使系统较易实现。由图1 易得

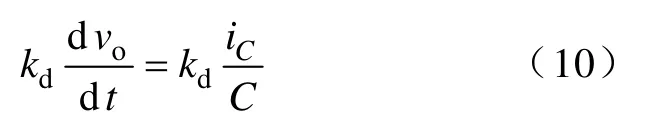
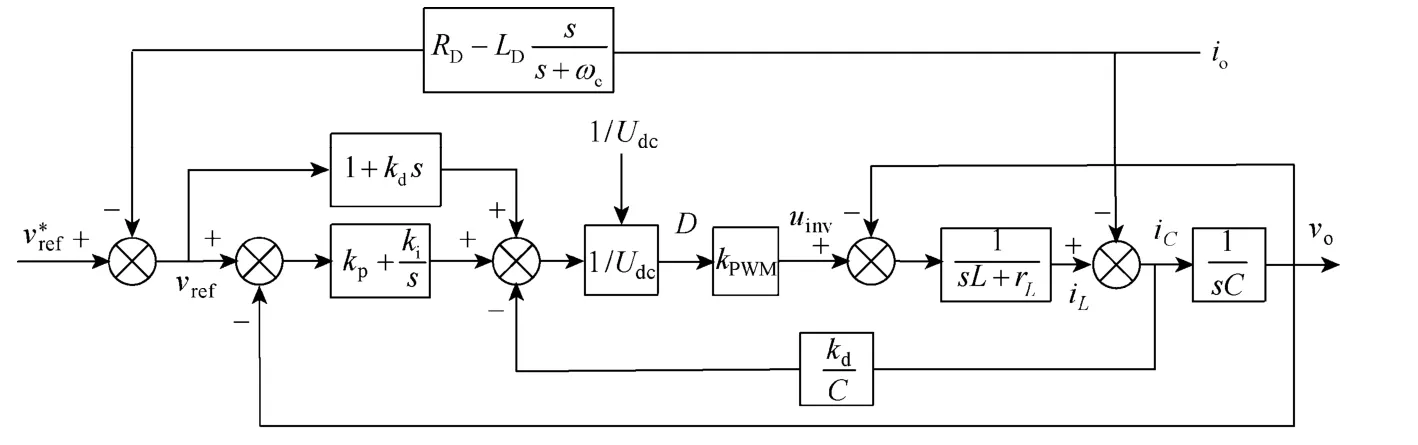
图6 基于虚拟复阻抗的电压控制框图Fig.6 Block diagram of the control of output voltage based on virtual complex impedance

即电容电压的微分可用电容电流iC的运算来代替。

5.2 下垂控制策略

利用图6 所示设计方法，通过选取合适的参数，由式（9）计算得出的逆变器输出阻抗呈电阻性。下面针对输出阻抗为上述幅频特性的并联逆变器下垂控制策略进行研究。

图7 所示为含有两个分布式电源的低电压微电网结构简图，R1、R2分别为逆变器1、2 输出电阻，Zline1=Rline1+jXline1、Zline2=Rline2+jXline2分别等效逆变器1、2 线路阻抗，Rline1远大于Xline1、Rline2远大于Xline2；Zload为负载阻抗。E1∠φ1和E2∠φ2分别为逆变器1、2 的空载输出电压，φ1、φ2分别为逆变器1、2 空载输出电压与负载电压V∠0°的相角差。

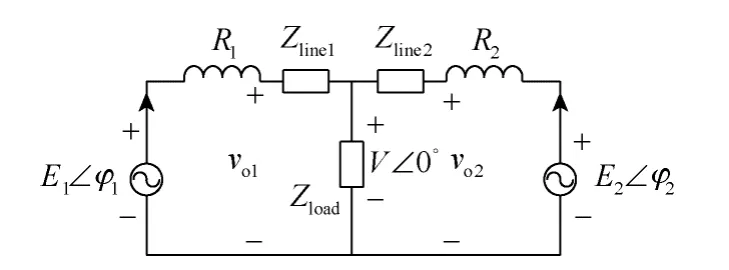
图7 含两个分布式电源的低电压微电网简化原理图Fig.7 Schematic diagram of the low voltage microgrid with two distributed generations

对各逆变器，设逆变器的输出电阻和线路电阻之和为R，则R的值远大于线路感抗值，线路感抗值可忽略不计。逆变器输出的有功功率和无功功率分别为[17]

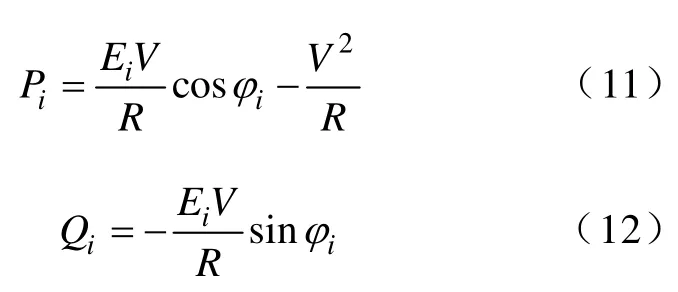
式中，Pi、Qi分别为逆变器i输出的有功功率和无功功率值；φi的值很小，可近似认为cosφi≈1，sinφi≈φi。

根据传统感性输出阻抗条件下的下垂控制原理，则阻性条件下的下垂控制方程变为

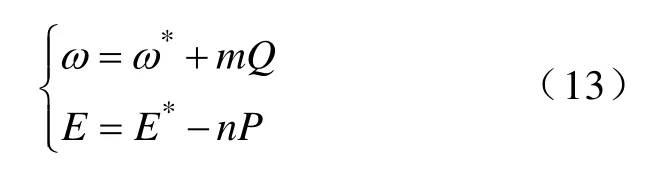
式中，ω*为空载角频率参考值；E*为空载输出电压幅值参考值。

下垂控制法采用的是平均功率控制，所以系统输出的瞬时有功功率p和瞬时无功功率q要通过低通滤波器滤波，才可以分别得到式（13）中的P和Q。同时，对式（13）中角频率下垂方程作如下修正

其中

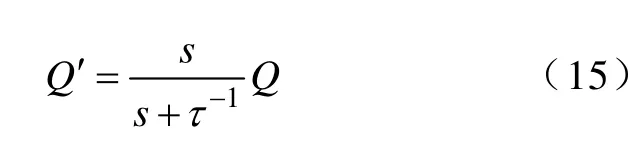
式中，τ为暂态下垂时间常数。利用式（15）可将Q中的直流分量滤除，在负载动态变化时，各并联逆变器输出频率与参考频率保持一致，可实现并联系统稳态输出频率的无差控制[18,19]。

由瞬时有功功率p和瞬时无功功率q计算得到平均功率P和Q'的公式可写为

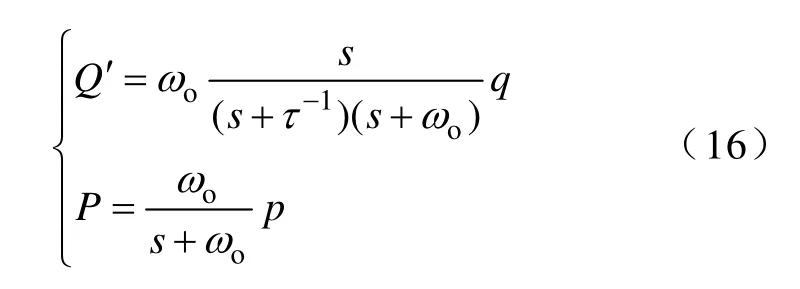
式中，ωo为低通滤波器的截止频率。

基于以上分析的下垂控制器结构如图8 所示。

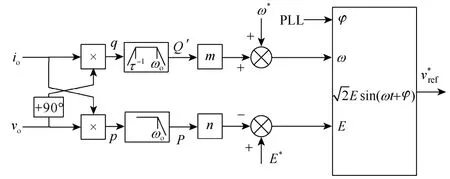
图8 下垂控制器结构框图Fig.8 Schematic diagram of the droop controller

6 仿真和实验结果

根据前文提出的低电压微电网中多逆变器并联运行控制策略，利用Matlab/Simulink 仿真平台搭建了两逆变器并联仿真模型，逆变器额定容量均为2kV·A，载波频率为10kHz，但线路阻抗差异较大且基本呈电阻性。利用本文提出的方法进行分析时，系统结构如图1 所示，逆变器电压控制器如图6 所示，下垂控制器如图8 所示。由前文的仿真分析，重新选取表2 中所示仿真参数。

图9 为采用未引入虚拟复阻抗、传统下垂控制法的仿真电流波形图；图10 为采用本文提出的方法仿真电流波形图。i1、i2分别为流过逆变器1、2 线路的电流，iH=(i1-i2)/2 为两逆变器之间的环流。0.6s之前只有逆变器1 单独运行，iH=i1/2；0.6s 逆变器2并入系统，电流i1逐渐变为原来的一半。经过短暂的过渡后，iH基本趋向于零。然而对比两者稳态电流波形可见，图10 中环流幅值相对图9 中较小，并联均流效果明显改善。

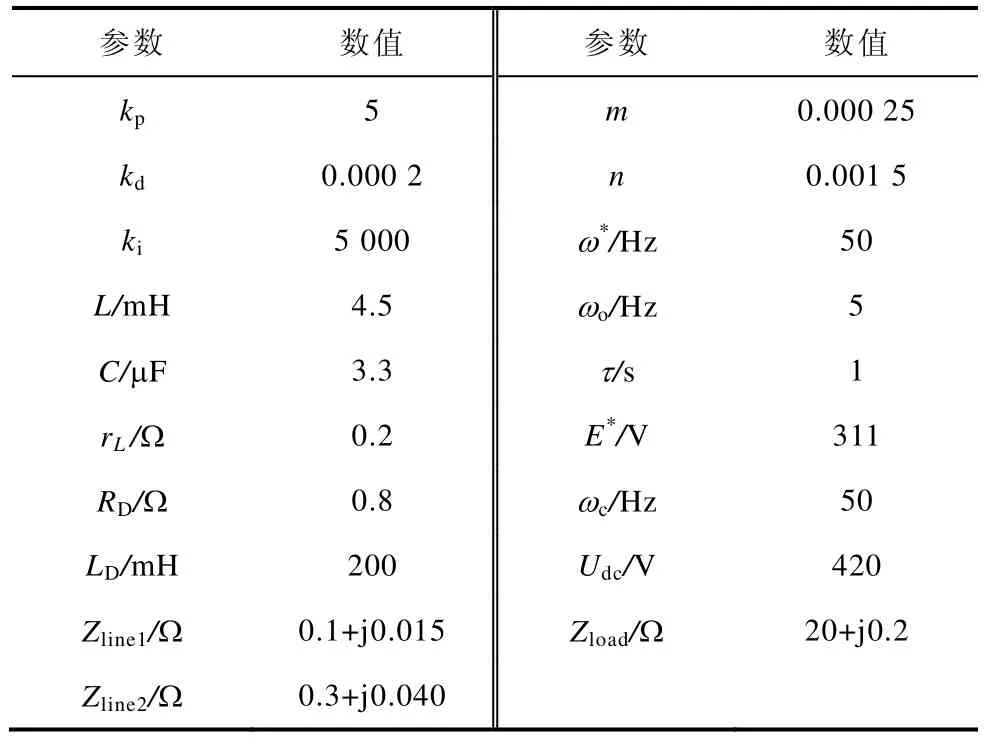
表2 仿真参数Tab.2 Simulation parameters

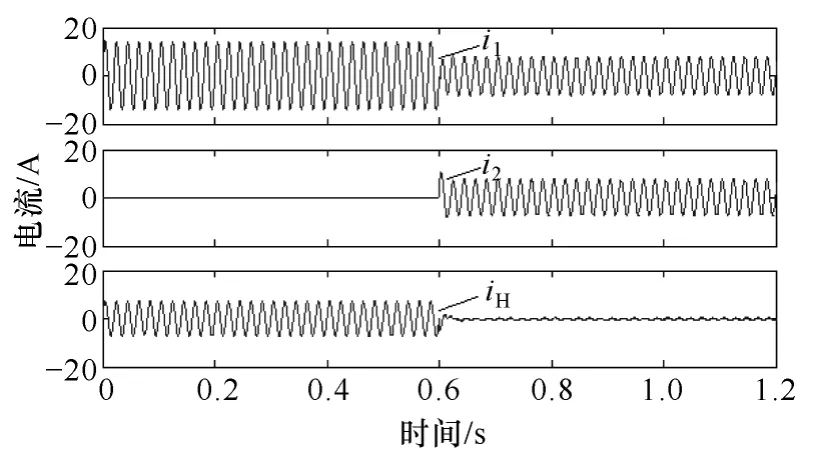
图9 传统控制策略仿真结果Fig.9 Simulation results of the traditional control method

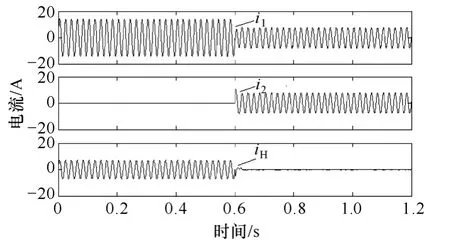
图10 提出的控制策略仿真结果Fig.10 Simulation results of the proposed control method

为进一步验证理论分析和仿真结果的有效性，在实验室搭建的2 台额定容量为2kV·A 的单相光伏逆变器并联系统平台上进行了实验验证。逆变器主电路采用全桥拓扑，采样及控制芯片采用TMS320F2812（DSP）。采用提出的基于虚拟复阻抗的电压控制策略，参数仍如表2 中所示，考虑到易操作性，载波频率采用12.8kHz。图11 所示为实验装置图。

图11 光伏逆变器并联系统平台Fig.11 Platform of parallel photovoltaic inverters system

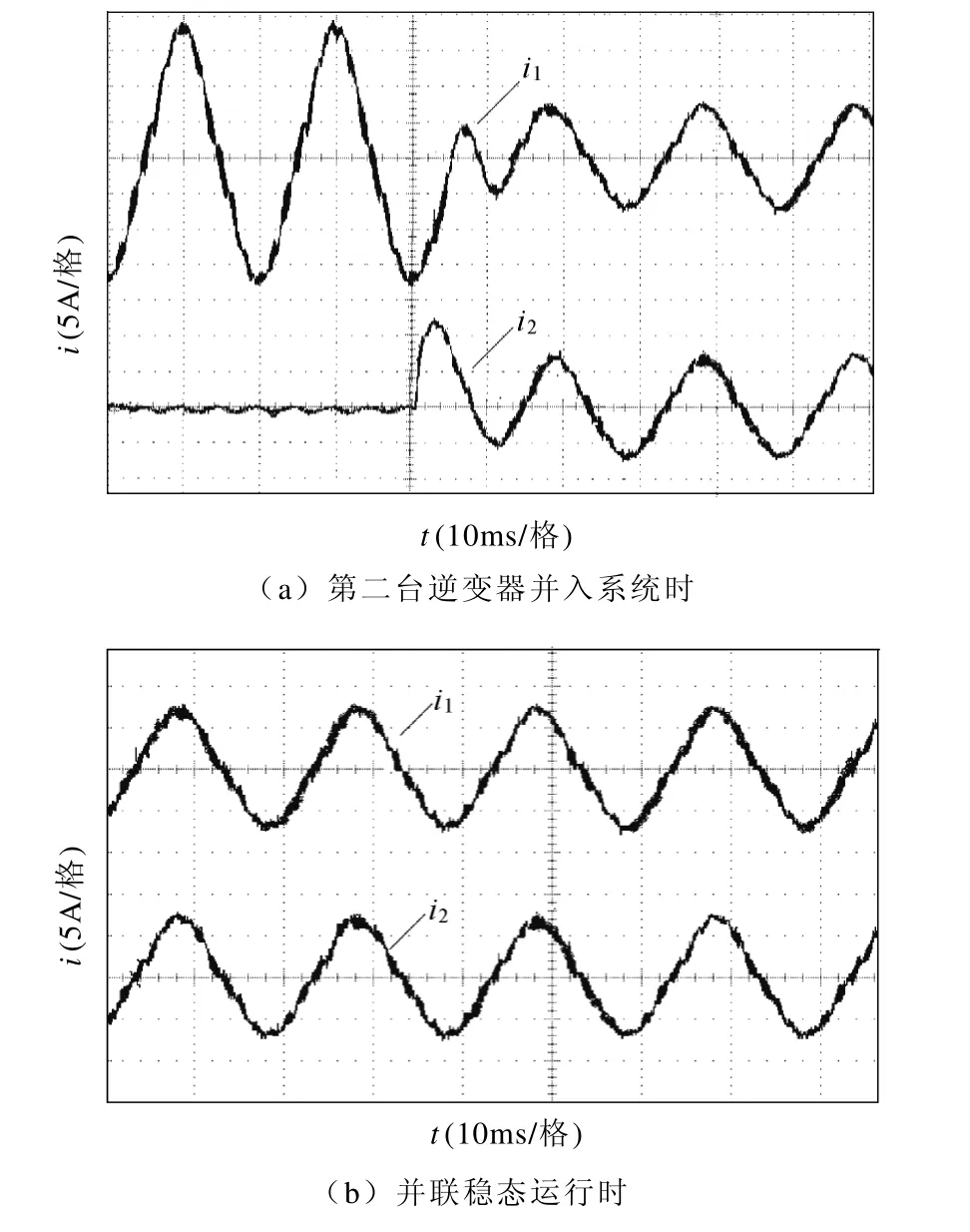
图12 输出电流实验波形图Fig.12 Experimental waveforms of output current

图12 所示为输出电流实验波形图，其中图12a为第二台逆变器并入系统时，两台逆变器输出电流变化图，图12b 为并联稳态运行时两逆变器输出电流。可见，实验结果与前述仿真结果分析基本一致，即使在线路阻抗不同且基本呈电阻性的条件下，低电压微电网多逆变器并联系统也具有较好的均流性能，输出电流的暂态过程、稳态过程均取得很好的效果。

可见，这种基于虚拟复阻抗的电压控制策略，适用于低电压微电网多逆变器并联控制，能够有效提高系统功率分担的精确性和稳定性，取得较好的运行效果。

7 结论

通过引入虚拟复阻抗，虚拟电阻增大逆变器输出电阻值；而虚拟感抗为负值，呈电容性，可降低逆变器输出阻抗中固有的感性分量，从而使逆变器输出阻抗在工频下呈纯阻性；通过幅频特性分析，详细地探讨了不同控制参数对于输出阻抗的影响，选取了合适的控制参数，给出了相应的下垂控制方法。以上基于虚拟复阻抗的电压控制策略，适用于低电压微电网多逆变器并联控制，能够有效提高系统功率分担的精确性和稳定性，取得了较好的运行效果。仿真与实验验证了该控制策略的可行性。

[1]王成山,李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34(2):10-16.Wang Chengshan,Li Peng.Development and challenges of distributed generation,the microgrid and smart distribution system[J].Automation of Electric Power Systems,2010,34(2):10-16.

[2]鲁宗相,王彩霞,闵勇,等.微电网研究综述.电力系统自动化[J].2007,31(19):100-105.Lu Zongxiang,Wang Caixia,Min Yong,et al.Overview on microgrid research[J].Automation of Electric Power Systems,2007,31(19):100-105.

[3]王成山,肖朝霞,王守相.微网中分布式电源逆变器的多环反馈控制策略[J].电工技术学报,2009,24(2):100-107.Wang Chengshan,Xiao Zhaoxia,Wang Shouxiang.Multiple feedback loop control scheme for inverters of the micro source in microgrids[J].Transactiona of China Electrotechnical Society,2009,24(2):100-107.

[4]姚玮,陈敏,陈晶晶,等.一种用于无互联线逆变器并联的多环控制方法[J].电工技术学报,2008,23(1):84-88.Yao Wei,Chen Min,Chen Jingjing,et al.An improved wireless control strategy for parallel operation of distributed generation inverters[J].Transactiona of China Electrotechnical Society,2008,23(1) :84-88.

[5]王成山,杨占刚,王守相,等.微网实验系统结构特征及控制模式分析[J].电力系统自动化,2010,34(1):99-105.Wang Chengshan,Yang Zhangang,Wang Shouxiang,et al.Analysis of structural characteristics and control approaches of experimental microgrid systems[J].Automation of Electric Power Systems,2010,34(1):99-105.

[6]Li Yunwei,Kao Chingnan.An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltage multibus microgrid[J].IEEE Transactions on Power Electronics,2009,24(12):2977-2988.

[7]Yu Xiaoxiao,Khambadkone A M,Huanhuan Wang,et al.Control of parallel-connected power converters for low-voltage microgrid—Prat I:a hybrid control architecture[J].IEEE Transactions on Power Electronics,2010,25(12):2962-2970.

[8]Guerrero J M,Vasquez J C,Matas J,et al.Control strategy for flexible microgrid based on parallel line-interactive UPS systems[J].IEEE Transactions on Industrial Electronics,2009,56(3):726-735.

[9]Guerrero J M,Vasquez J C,Matas J,et al.Hierarchical control of droop-controlled AC and DC microgrids—a general approach towards standardization[J].IEEE Transactions on Industrial Electronics,2011,58(1):158-172.

[10]Wei Yao,Min Chen,Matas J,et al.Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing[J].IEEE Transactions on Industrial Electronics,2011,58(2):576-588.

[11]Chandrokar M C,Divan D M,Adapa R.Control of parallel connected inverters in standalone ac supply systems[J].IEEE Transactions on Industry Applications,1993,29(1):136-143.

[12]Li Yunwei,Vilathgamuwa D M,Poh Chiang Loh.Design,analysis,and real-time testing of a controller for multibus microgrid system[J].IEEE Transactions on Power Electronics,2004,19(5):1195-1204.

[13]De Brabandere K,Bolsens B,Van den Keybus J,et al.A voltage and frequency droop control method for parallel inverters[J].IEEE Transactions on Power Electronics,2007,22(4):1107-1115.

[14]Li Yan,Li Yunwei.Decoupled power control for an inverter based low voltage microgrid in autonomous operation[C].IEEE 6th International Power Electronics and Motion Control Conference,Wuhan,China,2009.

[15]Laaksonen H,Saari P,Komulainen R.Voltage and frequency control of inverter based weak LV network microgrid[C].IEEE International Conference on Future Power Systems,Amsterdam,Holland:2005:1-6.

[16]Zhong Qingchang.Robust droop controller for accurate proportional load sharing among inverters operated in parallel[J].IEEE Transactions on Industrial Electronics,2013,60(4):1281-1290.

[17]Guerrero J M,Matas J,Luis Garcia de Vicuna,et al.Decentralized control for parallel operation of distributed generation inverters using resistive output impedance[J].IEEE Transactions on Industrial Electronics,2007,54(2):994-1004.

[18]Guerrero J M,Matas J,De Vicuna L G,et al.Wireless-control strategy for parallel operation of distributed-generation inverters[J].IEEE Transactions on Industrial Electronics,2006,53(5):1461-1469.

[19]Guerrero J M,Garcia de Vicuna L,Matas J,et al.Output impedance design of parallel-connected UPS inverters with wireless load-sharing control[J].IEEE Transactions on Industrial Electronics,2005,52(4):1126-1135.