级联型多电平逆变器线电压谐波优化的SVPWM 策略

李继华 阮新波 王学华

（华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074）

1 引言

多电平逆变器具有开关管电压应力低、电压变化率（dv/dt）小、输出电压谐波含量小等优点，特别适用于中高压大功率场合[1-3]。近年来，多电平逆变器的研究主要集中在拓扑结构[4]、矢量控制[5,6]以及在某些场合的应用[7]（例如光伏、风电、大电机驱动等）。多电平逆变器可分为二极管钳位型、飞跨电容钳位型和级联型三种[3,8-12]，其中级联型多电平逆变器不存在前两者的输入电容均压或飞跨电容电压控制问题，而且结构最简单，易于模块化设计，因此一直在中高压大功率场合备受青睐[3,8-9]。

级联型多电平逆变器常见的调制策略有正弦脉宽调制（Sinusoidal Pulse-Width Modulation,SPWM）和空间矢量调制（Space Vector Pulse-Width Modulation,SVPWM），其中SPWM 可分为同向层叠（Phase Disposition,PD）、反向层叠（Phase Opposition Disposition,POD）、交错反向层叠（Alternative Phase Opposition Disposition,APOD）和载波移相（Carrier Phase Shift,CPS）四种[9,13-15]。若级联单元数为m，这些调制方式输出的最低次开关谐波分布在2m倍开关频率附近。对于三相三线制级联多电平逆变器而言，PD 调制方式的线电压谐波最小，但各个H 桥输出功率不均衡，各H 桥开关管的开关次数也不等；采用CPS 调制方式时，各H 桥开关管的开关次数相等，且可实现输出功率自然均衡[13-17]。文献[16]提出一种改进型PD，它利用几组梯形载波将PD和CPS 两种调制方式结合起来，使得这种调制方式既具有PD 的线电压谐波小的优点，又具有CPS 的各H 桥之间功率均衡且开关管开关次数相等的优点。然而，改进的PD 所需梯形载波个数较多，不易在数字芯片内生成。针对这一不足，文献[18]提出了一种基于状态机的实现方法，有效简化了改进型PD 调制的实现。

作为级联多电平逆变器另一种常用的调制策略，SVPWM 相对于SPWM 具有直流电压利用率高，输出谐波小等优点，被广泛应用于三相系统中，近年来已受到人们的关注[19-28]。对于两电平逆变器而言，SVPWM 所有开关管总共只有8 个开关矢量，实现非常容易。对于多电平逆变器而言，SVPWM的开关矢量个数随着电平数增加呈级数增加，因此传统的SVPWM 会占用很长的计算时间，实现难度大为增加。目前有一些针对多电平逆变器SVPWM的改进，主要是优化计算时间[22-24]和从整体上把多电平空间矢量控制简化为电平数更少的空间矢量控制[25-28]。

本文首先分析级联型多电平逆变器的一种能够大量减少计算过程的简化SVPWM 控制算法的实现机理，在此基础上，将改进PD 调制方式的实现思路应用于该简化SVPWM 控制算法，提出具有PD和CPS 控制二者优点的SVPWM 控制算法。所提出的SVPWM 控制算法实现简单、输出线电压谐波含量小、可自然实现各H 桥单元功率均衡以及各开关管开关次数一致等优点。在实验室研制了一台三相4.5kW 级联五电平逆变器的原理样机，对所提出的SVPWM 控制算法有效性进行了验证。

2 基于CPS 的多电平空间矢量控制

图1 给出了m个H 桥单元的三相级联型多电平逆变器，每相最多可输出(2m+1)个电平，对应三相开关矢量个数为(2m+1)3。

图1 级联型多电平逆变器电路拓扑Fig.1 Topology of cascaded multi-level inverter

SVPWM 以三相合成的空间电压矢量为控制对象，能够提高逆变器的直流电压利用率[19,20]。传统SVPWM 实现方式[24]为：确定合成矢量所处的三角形区域，然后计算构成该区域的三个基本矢量的作用时间并通过调制产生相应的PWM 信号。随着电平数的增加，三角形区域和基本矢量个数相应增多，上述过程非常复杂，在数字控制中实现很困难。

2.1 简化的多电平空间矢量控制

根据图1 可得三相电压

式中，m为级联单元的个数。任意时刻的合成矢量V=(vA，vB，vC)T可以表示为

式中，VRi=(vRiA，vRiB，vRiC)T，VLi=(vLiA，vLiB，vLiC)T，i=1,2,…,m。

从式（2）可以看出，合成矢量V可分解为VR1、VL1、VR2、VL2…VRm、VLm这2m个矢量[28]，如图2所示。对于每个矢量（VRi或VLi）而言，可以采用两电平空间矢量合成进行控制。当VR1、VR2、…VRm之间依次相差θ，且

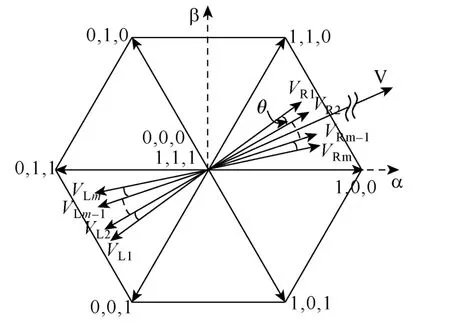
图2 简化电平空间矢量方法Fig.2 Level-simplified space vector diagram

输出相电压中2～2(m-1)倍开关频率附近的谐波可以被消除。式（3）中Nv为载频比。

需要说明的是，由于VLi和VRi是第i个H 桥单元左右桥臂中点电压矢量，在结构上每个H 桥输出电压为右桥臂电压与左桥臂电压之差，其电压基波是叠加的，所以VLi与VRi反相。

文献[28]把复杂的多电平空间矢量简化为两电平空间矢量，并保留了多电平逆变器谐波小的优点。但是，将V直接分解为VRi与VLi(i=1,2,…,m)2m个矢量的计算过程比较复杂，而VRi是相角不同的m个矢量，这意味着要进行m个两电平空间矢量的计算。另外，对于VRi、VLi这2m个两电平空间矢量而言，它们的最大电压利用率都为1.15，但VRi之间及VLi之间存在相角差，因此V的幅值必然小于VR1幅值的2m倍。即按式（2）进行合成时，总的电压利用率将不足1.15。

2.2 基于CPS 的多电平SVPWM 控制

从每个H 桥单元来看，由于矢量VRi与VLi反向，每个H 桥单元的中点电压(Vi=VRi-VLi)为三电平波形，其最低次谐波在2 倍载波频率处。为了消除2～2(m-1)倍载波频率处的谐波，可以借鉴CPS调制方式的特点：采用一个调制波分别与多个移相载波进行比较，来消除2～2(m-1)倍载波频率处的谐波。

基于以上思路，本文提出一种基于CPS 控制的级联型多电平SVPWM 方法。令2m个两电平矢量满足：VR1=VR2=…=VRm=V/(2m)；VL1=VL2=…=VLm=-V/(2m)，总输出电压在幅值上就等于两电平空间矢量输出电压的2m倍。同时将载波依次移相π/m，分别得到2m条载波。这里以五电平为例，如图3 所示，4 条载波为Carrier1～Carrier4，依次移相π/2。三相调制波mA、mB、mC分别与它们进行比较，最终得到每一组桥臂的PWM 信号，图中给出了Sa11，Sa14，Sa21，Sa24，Sb11，Sb14，Sb21，Sb24，Sc11，Sc14，Sc21，Sc24共12 路开关管的驱动波形，对应的上、下管互补工作。

图3 基于载波移相的多电平SVPWMFig.3 CPS based SVPWM for multi-level inverter

对于m个H 桥单元的级联多电平逆变器而言，这种移相式SVPWM 调制方式输出电压的谐波类似于CPS 调制方式，总输出电压主要的谐波将分布在2m倍载波频率附近。

与文献[28]的方法相比，基于 CPS 的多电平SVPWM 减少了矢量分解，只需进行一次两电平空间矢量计算即可，计算过程大为简化；同时直流电压最大利用率可达到1.15。

3 基于改进PD 的多电平SVPWM 控制

3.1 改进PD 调制策略

在多电平逆变器的4 种SPWM 调制方式中，PD调制方式输出线电压谐波最小[17,18]，但它存在各H桥单元功率不均衡，且开关管开关次数不一致的缺点。文献[16]提出了一种改进型PD，这种调制方式结合了PD 与CPS 的优点：保留PD 线电压谐波最优，各H 桥单元可实现功率自然均衡，各H 桥单元开关管开关次数一致。

以五电平逆变器为例，如图4 所示，R1桥臂开关管Sa11、Sa12的驱动由A 相调制波与Carriers1 比较得到，而Carriers1 由Carrier11～Carrier14 构成。调制过程需要对调制波的瞬时值进行判断：当调制波位于第一层时与Carrier11 交截得到Sa11的驱动PWM 波，调制波高于Carrier11 时，PWM 波为高电平，反之则为低电平，而Sa12与Sa11互补工作。当调制波位于第二、三、四层时将分别与Carrier12、Carrier13、Carrier14 交截进行调制。类似地，载波Carriers2～Carriers4 也是分别由四层载波构成，它们相对于Carriers1 而言依次移相了π/2。同样地，R2、L1、L2桥臂开关管的驱动分别由调制波与Carriers2、Carriers3、Carriers4 调制生成。在一个载波周期内，调制波分别与Carriers1～Carriers4 各交截一次，对应的4 个桥臂的开关管各动作一次；同时每个H 桥输出电压基波为Vi=VRi-VLi=V/2，每相m个H 桥单元是串联关系（即电流相等），所以各H 桥传输功率相等。因此改进PD 具备了CPS调制方式功率自然均衡和开关管开关次数一致的优点。

图4 改进PD 调制方式的载波Fig.4 The carriers of improved PD

3.2 基于改进PD 的多电平SVPWM 控制

改进PD 结合了PD 与CPS 二者的优点，把这一思路应用于前面提出的基于 CPS 的多电平SVPWM 控制之中，使得输出线电压的谐波得到进一步优化。

这里只要把由VRi与VLi(i=1,2,…,m)计算得到的三相调制波mA、mB、mC分别与图5 所示的2m组载波分别进行调制即可。

图5 基于改进PD 的SVPWM 调制方式Fig.5 PD based SVPWM for multi-level inverter

以五电平为例，如图5 所示，粗实线、细实线、粗虚线、细虚线分别为Carriers1～Carriers4，图中给出了Sa11，Sa14，Sa21，Sa24，Sb11，Sb14，Sb21，Sb24，Sc11，Sc14，Sc21，Sc24共12 只开关管的开断信号，它们对应的上下管互补工作。

基于改进PD 的SVPWM 确实能够较好地结合PD、CPS和SVPWM 的优点，但因为在调制波与载波比较生成 PWM 波的过程，需要判断调制波位于哪一层，然后选择对应的载波（对五电平则为 Carrier11～Carrier14，Carrier21～Carrier24，Carrier31～Carrier34，Carrier41～Carrier44）与之交截。若有m个H 单元级联，则调制过程涉及到的载波共有4m2个，数量较多，且这些载波与传统的锯齿或三角载波相比，其波形不规则，在数字控制实现上有一定的难度。

4 调制过程的实现

调制过程是调制波与载波交截产生PWM 驱动的过程。交截点是随着调制波变化而变化，注意到，相邻两交截点之间开关管的开关状态并没有变化。通过判断相邻两个开关状态的切换条件同样可以实现PWM 调制过程。本文应用该方法，实现改进PD的SVPWM 控制算法。

4.1 开关状态的分析

图6 给出了改进PD 调制方式与PD 调制方式的对比。图6a是改进PD 调制方式，这里把图4 的四组载波放在一起，按照调制波与四路载波的关系在载波周期内把图6a 分成32 个三角形区域，每一个区域对应一个4 位数字，其定义为：第一位是1 就表示调制波在该处与Carriers1 进行调制时比较输出为高电平，对应Sa11的驱动为高电平，Sa12的驱动为低电平，相反第一位是0。同样，第i(i=1,2,3,4)位是1 表示调制波在该处与Carriersi进行调制时比较输出为高电平；是0 则表示为低电平。

图6 PD 与改进PD 调制的联系Fig.6 The connection between PD and improved PD

这样，每个三角形的4 位数字就对应一种相电压的输出及其开关管的开关状态。以状态为 0111的三角形为例，当调制波在该区间内时，它比Carriers1 低，但比Carriers2～Carriers4 高，所以开关管Sa11驱动为低电平，Sa21、Sa14、Sa24驱动为高电平，此时a 相输出电压为E。依次类推，在改进PD 调制方式中，状态1111 对应逆变器输出2E；状态0111、1011、1101、1110 对应逆变器输出E；状态0110、0011、1001、1100 对应逆变器输出0；状态0100、0010、0001、1000 对应逆变器输出–E；状态0000 对应逆变器输出–2E。

对于PD 调制方式，如图6b 所示，由于它的载波是层叠的4 路，按照调制波与4 路载波的关系，同样的定义可以发现它只有1111、0111、0011、0001和0000 五种开关状态，逆变器输出相电压分别对应为2E、E、0、–E和–2E。

通过上述分析，对比改进PD和PD 可以发现，在输出电压为E、0、–E时，前者多利用了1011、1101、1110、0110、1001、1100、0100、0010、1000共9 个冗余的开关状态，但并没改变逆变器的输出电压，所以同样的调制波分别与图6 两种载波比较得到的逆变器总输出电压波形是完全一样的，谐波分布也就一样。但是改进PD 的载波具有了CPS 载波移相的特点，因此各个开关管开关次数一致，且各H 桥传输功率均衡。

4.2 基于改进PD 的SVPWM 控制的状态机实现

图6a 的改进PD 调制方式，其每个三角形区间有一个4 位数表示调制波与各路载波的关系，它对应一种开关状态，也即对应一种逆变器输出电平。

在如图6a 所示的一个载波周期内共有32 个开关状态，为陈述方便，将32 个开关状态所在的三角形编号为1～32。

现在对改进PD 调制方式在数字控制下整个调制过程进行分析。取图6a 中0111 的区域为例，当调制波在这个区间时，随着时间的变化，调制波的位置可能出现四种情况：仍然在0111 的区间；上跳到1111 的区间；下跳到0110 的区间；向右到0011的区间，如图7 所示。这个过程可以用右边的状态切换图来表示，而状态跳变的条件是图中的sta值，它表示一个载波周期内调制波所处三角形的编号，可以通过调制波的值与三角载波比较得到，其取值范围为1～32，这样根据sta的取值就知道该时刻调制波的位置。

图7 逆变器输出状态的切换Fig.7 The output state change of the inverter

把一个周期内的所有区间的状态切换过程结合起来，可以得到图8 所示的时序逻辑图，每一椭圆里标注当前输出的开关状态，括号内的数字即为sta的取值。通过判断sta来判断和改变系统下一次的输出状态，即各个开关管的PWM 信号，从而实现从一个状态切换到下一状态，这样调制过程不需要构建数量多且波形复杂的载波。

5 实验验证

为验证本文提出的SVPWM 控制算法，在实验室研制了一台三相4.5kW 级联五电平逆变器原理样机，各H 桥单元输入电压源电压均为E=180V，开关管开关频率fc=5kHz，输出等效开关频率fe=20kHz。

图9 给出了逆变器输出滤波后的相电压和线电压波形。由图9 可见，输出相电压可等效为在正序基波里面注入了零序电压，能够把电压利用率提高到1.15。三相线电压波形正弦，频率为50Hz，有效值为380V。

图8 改进PD 调制方法基于状态机的实现Fig.8 Achievement of improved PD based on state machine

图9 系统输出电压波形Fig.9 The output voltage waveforms

图10 给出了基于CPS 的SVPWM 控制算法实验波形。图10a是滤波后线电压vab、逆变桥输出的相电压vA和线电压vAB。图10b是对vA和vAB进行FTT 分析的频谱图。可以看出，最低次开关谐波同样分布在20kHz 附近。图10c是vA和vAB在20kHz附近展开的频谱图。同CPS 调制方式类似，相电压中主要次开关谐波位于20kHz 附近，该主要次开关谐波在线电压中是叠加的。

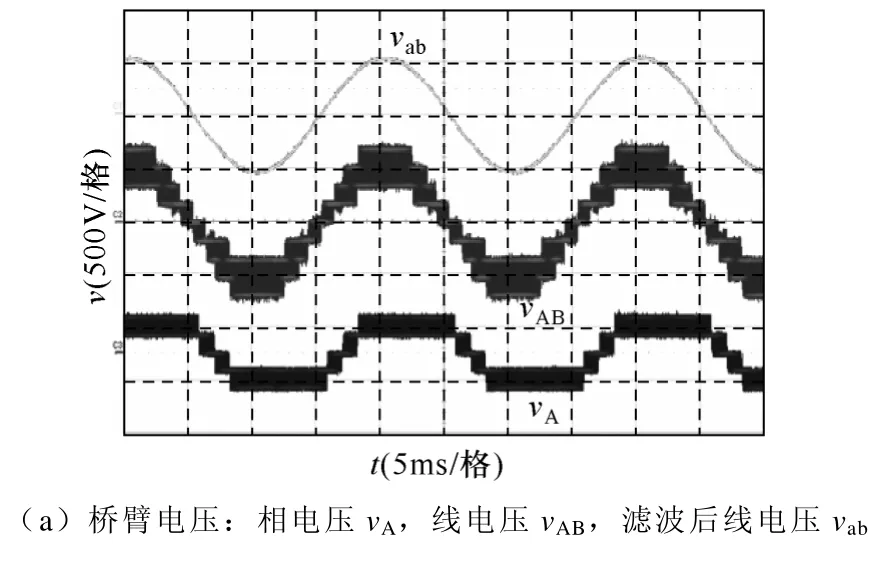
图10 基于CPS 的SVPWM 调制下的波形及频谱Fig.10 The waveforms and spectrum of SVPWM based on CPS

图11是本文提出的基于改进PD 的SVPWM 控制算法两H 桥单元输出电压和对应瞬时功率的实验波形。借助功率分析仪测得H1桥和H2桥输出功率的平均值分别为770W和760W，说明两H 桥自然实现了功率均衡。又因为每个载波周期内调制波仅与载波交截一次，对应开关管动作一次，因此提出的SVPWM 控制算法也具有CPS 调制方式开关管开关次数一致的优点。

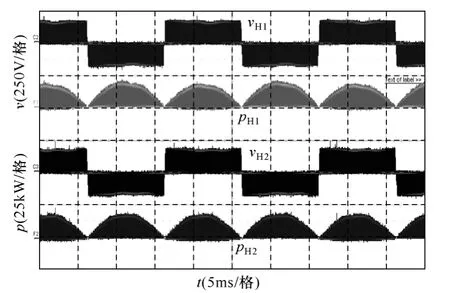
图11 改进PD 的SVPWM 调制两H 桥输出电压和功率Fig.11 The voltage and power of two H-bridges of SVPWM based on improved PD

图12 改进PD 的SVPWM 调制下的波形及频谱Fig.12 The waveforms and spectrum of SVPWM based on the improved PD

图12是基于改进PD 的SVPWM 控制算法实验波形。图12a是滤波后线电压vab、逆变桥输出的线电压vAB和相电压vA。图12b是对vA和vAB进行FTT分析的频谱图。可以看出，最低次开关谐波同样分布在20kHz 附近。图12c是vA和vAB在20kHz 附近展开的频谱图。同PD 调制方式类似，相电压中主要次开关谐波位于20kHz 处，该主要次开关谐波在线电压中被自然抵消。

比较图10c和图12c 可以发现：前者等效于CPS调制方式，后者等效于PD 调制方式，前者相电压中的主要次开关谐波在线电压中是叠加的，而后者的线电压中主要次开关谐波被自然抵消，因此后者线电压总的谐波较小。这表明本文提出的SVPWM控制算法在三相系统中具有更低的线电压谐波，从而有利于减小输出滤波器。

上述实验结果表明：基于本文提出的SVPWM控制算法，能够有效降低SVPWM 控制算法的复杂度，各H 桥单元功率自然实现均衡，开关管开关次数达到一致，同时输出线电压谐波更小。有效结合了CPS、PD、SVPWM 三者的优点。

6 结论

本文提出了一种适合于级联型多电平逆变器的SVPWM 控制算法。通过将合成矢量等效为2m个两电平矢量叠加（m为级联单元的个数），多电平的SVPWM 调制可简化为2m个传统两电平SVPWM的移相叠加。通过将生成PWM 脉冲序列的载波重构，可以使输出线电压开关谐波含量更小，同时各H 桥单元输出功率自然实现均衡，各开关管开关次数保持一致。采用状态机实现了所提出的SVPWM控制算法。

在实验室搭建了一台三相4.5kW 级联五电平逆变器原理样机，对传统 SVPWM和本文所提出的SVPWM 两种策略谐波进行了分析和比较，实验结果证明了本文提出的SVPWM 调制方式具有输出线电压谐波更小，可以自然实现各H 桥单元功率均衡，开关管开关次数一致等优点。

[1]Marcheoni M.High-performance current control techniques for applications to mulitilevel high-power voltage source inverter[J].IEEE Transactions on Power Electronics,1992,7(1):189-204.

[2]Nami A,Zare F,Ghosh A,et al.A hybrid cascaded converter topology with series-connected symmetrical and asymmetrical diode-clamped H-bridge cells[J].IEEE Transactions on Power Electronics,2011,26(1):51-65.

[3]Tolbert L,Peng F Z,Haberler T G.Multilevel converters for large electronics drives[J].IEEE Transactions on Industry Applications,1999,35(1):36-44.

[4]Alain S R,Mikel M,Silverio A,et al.Medium voltage high power converter topologies comparison procedure,for a 6.6kV drive application using 4.5kV IGBT modules[J].IEEE Transactions on Industrial Electronics,2012,59(3):1462-1476.

[5]Mekhilef S,Mohamad N.A K.Novel vector control method for three stage hybrid cascaded multilevel inverter[J].IEEE Transactions on Industrial Electronics,2011,58(4):1339-1349.

[6]Khoucha F,Mouna S L,Abdelaziz K,et al.A comparison of symmetrical and asymmetrical three phase H-bridge multilevel inverter for DTC induction motor drives[J].IEEE Transactions on Energy Conversion,2011,26(1):64-72.

[7]Marcelo C C,Alexandre M F,Kleber C O,et al.Eliminating leakage currents in neutral point clamped inverters for photovoltaic systems[J].IEEE Transactions on Industrial Electronics,2012,59(1):435-443.

[8]Corzine K,Familiant Y.A new cascaded multilevel H-bridge drive[J].IEEE Transactions on Power Electronics,2002,17(1):125-131.

[9]McGrath B P,Holmes D G.A comparison of multicarrier PWM strategies for cascaded and neutral point clamped multilevel inverters[C].Proceedings of IEEE Power Electronics Specialists Conference(PESC),2000:674-679.

[10]Nabae A,Takahashi I,Akagi H.A new neutral-pointclamped PWM inverter[J].IEEE Transactions on Industry Applications,1981,17(5):518-523.

[11]Pradeep M B,Stefanovic V R.Generalized structrue of a multilevel PWM inverter[J].IEEE Transactions on Industry Applications,1983,19(6):1057-1069.

[12]Escalante M F,Vannier J C,Arzande A.Flying capacitor multilevel inverters and DTC motor drive applications[J].IEEE Transactions on Industrial Electronics,2002,49(4):809-815.

[13]Carrara G,Gardella S,Marchesoni M,et al.A new multilevel PWM method:a theoretical analysis[J].IEEE Transactions on Power Electronics,1992,7(3):497-505.

[14]Dixon J W,Ooi B T.Dynamically stabilized indirect current controlled SPWM boost type 3-phase rectifier[J].Proceedings of IEEE Industry Applications Society (IAS) Annual Meeting,1988:700-705.

[15]王学华,张欣,阮新波.级联型多电平逆变器最优SPWM 控制策略及其功率均衡方法[J].电工技术学报,2009,24(5):92-99.Wang Xuehua,Zhang Xin,Ruan Xinbo.Optimal SPWM control strategy and its power balance scheme for cascaded multilevel inverters[J].Transactions of China Electrotechnical Society,2009,24(5):92-99.

[16]Kang D W,Lee Y H,Suh B S,et al.An improved carrierwave-based SVPWM method using phase voltage redundancies for generalized cascaded multilevel inverter topology[C].Proceedings of IEEE Applied Power Electronics Conference and Exposition(APEC),2000:542-548.

[17]McGrath B P,Holmes D G.Multicarrier PWM strategies for multilevel inverters[J].IEEE Transactions on Industrial Electronics,2002,49(4):858-867.

[18]McGrath B P,Meynard T,Gateau G,et al.Optimal modulation of flying capacitor and stacked multicell converters using a state machine decoder[J].IEEE Transactions on Power Electronics,2007,22(2):508-516.

[19]Lee Y H,Kim D H,Hyun D S.Carrier based SVPWM method for multilevel system with reduced HDF[C].Proceedings of IEEE Industry Applications Society(IAS) Annual Meeting,2000:1996-2003.

[20]Zhou K,Wang D.Relationship between space-vector modulation and three-phase carrier-based PWM:a comprehensive analysis[J].IEEE Transactions on Industrial Electronics,2002,49(1):186-196.

[21]Gupta A K,Khambadkone A M.A space vector modulation scheme to reduce common mode voltage for cascaded multilevel inverters[J].IEEE Transactions on Power Electronics,2007,22(5):1672-1681.

[22]Li Z,Wang P,Zhu H,Li Y.A new simplified and uniform space vector PWM method for n-level inverters[C].Proceedings of IEEE Industrial Electronics and Applications,ICIEA 2008:236-241.

[23]Leon J I,Vazquez S,Sanchez J A,et al.Convntional space-vector modulation techniques versus the single-phase modulator for multilevel converters[J].IEEE Transactions on Industrial Electronics,2010,57(7):2473-2482.

[24]姜旭,肖湘宁,赵洋,等.改进的多电平 SVPWM及其广义算法研究[J].中国电机工程学报,2007,27(4):90-95.Jiang Xu,Xiao Xiangning,Zhao Yang,et al.An improved multilevel SVPWM and its generalized algorithm[J].Proceedings of the CSEE,2007,27(4):90-95.

[25]Seo J H,Choi C H,Hyun D S.A new simplified space-vector PWM method for three-level inverters[J].IEEE Transactions on Power Electronics,2001,16(4):545-550.

[26]Gupta A K,Khambadkone A M.A space vector PWM scheme for multilevel inverters based on two-level space vector PWM[J].IEEE Transactions on Industrial Electronics,2006,53(5):1631-1639.

[27]Mekhilef S,Akadir M N.Novel vector control method for three-stage hybrid cascaded multilevel inverter[J].IEEE Transactions on Industrial Electronics,2011,58(4):1339-1349.

[28]史喆,石新春.级联型逆变器的一种新型 SVPWM方法[J].电工技术学报,2005,20(10):30-35.Shi Zhe,Shi Xinchun.A novel technique of SVPWM based on cascaded H-bridge multi-level inverter[J].Transactions of China Electrotechnical Society,2005,20(10):30-35.