几种AR和ARMA模型对城市用水量预测的比较

翁建华，廉东方，崔晓钰

（1.上海电力学院 能源与机械工程学院，上海200090；2.上海理工大学 能源与动力工程学院，上海200093）

城市用水量预测是通过对历史数据进行综合分析，并在基本趋势判断基础上，对未来时段的用水量作出预测。

用于城市用水量预测的方法有多种，如时间序列分析法、神经网络模型法［1-2］等。每种预测方法都有各自特点，针对具体问题选择合适方法十分重要［3-5］。对城市短期用水量预测，最常用的还是时间序列分析法。时间序列分析法包括自回归（AR）、移动平均（MA）、自回归移动平均（ARMA）、灰色预测法等［6］。

根据城市用水特点采用AR和ARMA模型，对城市某区域用水量进行预测，并比较了不同模型的预测结果。

1 城市短期用水量特点

城市短期用水量可分为时用水量、日用水量和周用水量，这些短期用水量受天气、季节、居民生活、社会活动及工业生产状况等因素的影响而变化。无异常情况下一周内工作日（周一至周五）的用水量变化特征是相似的，而周末与节假日的用水量则与工作日明显不同。一天内的时用水量基本上以24h为周期进行变化，且有夜晚低、白天高的特点。短期内无异常情况下，连续数个工作日 （或连续数个非工作日）同一时间段的用水量比较接近，连续几周日用水量的变化也有趋向于自身重复的特性。

某市一区域工作日的时用水量变化曲线如图1。

图1 工作日的时用水量变化

由图1可见，白天的用水量明显要高于夜晚，尤其凌晨零点至四点用水量达到一天的最低。

连续18个工作日的日用水量变化曲线如图2。

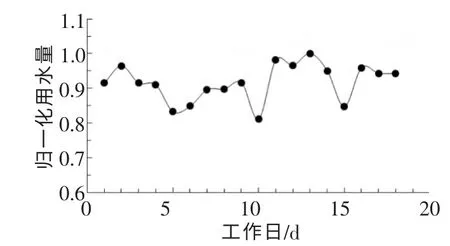
图2 工作日的日用水量变化

由图2可见，周五的日用水量通常为一周工作日的日用水量最低值。

2 用水量预测的时间序列分析法

城市用水量的短期预测常采用时间序列分析法。本文采用不同AR及ARMA模型［7-8］对某市一区域用水量进行预测，并对不同模型的预测结果进行比较。

2.1 自回归模型AR（p）

对于时间序列X1，X2，…Xt，…，采用AR（p）模型，则当前值Xt可表示为过去观察值Xt-1，Xt-2，……，Xt-p的线性组合：

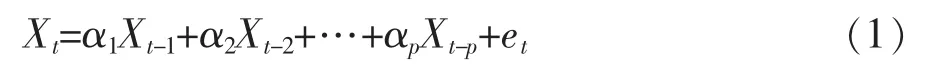
其中α1，α2，……，αp为模型参数；p为模型阶数；et为随机干扰。

2.2 自回归移动平均模型

对于时间序列X1，X2，…，Xt，…，采用ARMA（p，q）模型，则当前值Xt不仅与过去观察值Xt-1，Xt-2，…，Xt-p有关，还与过去时刻进入系统的扰动有关，则：

式中 α1，α2，…，αp和β1，β2，…，βq为模型参数；{ek}为白噪声过程；p，q为模型阶数。

无论是AR模型还是ARMA模型，都需要利用历史数据对模型参数进行估计。参数估计的方法有矩估计法、最小二乘法和极大似然估计法等。

预测模型的评价指标有相对误差、均方差（MSE）和平均绝对百分比误差（MAPE）等，计算方法有［9］：

2.2.1 相对误差Pi

相对误差Pi公式如下：

式中 ei=Fi-xi；xi为第i时刻的实际观测值；Fi为第i时刻的预测值。

2.2.2 均方差MSE

均方差MSE公式如下：

2.2.3 平均绝对百分比误差MAPE

平均绝对百分比误差MAPE公式如下：

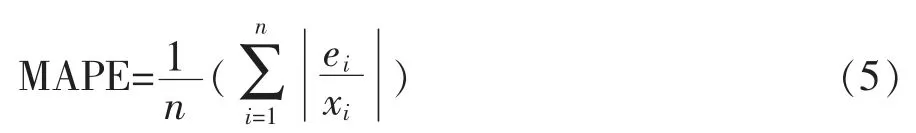
误差越小，则模型预测的精度越高。

3 预测结果及分析

利用17个连续工作日的时用水量，并对个别异常数据进行修复处理后，用AR模型预测得到的次日各时间段的时用水量如图3。

图3 时用水量AR模型预测

图3中的用水量进行了归一化处理。模型参数的估计采用最小二乘法。

AR模型预测结果与实测值之间的相对误差分布如图4。

图4 AR模型时用水量预测结果相对误差

由图4可见，相对误差均在±10%之内，且绝大多数在±5%之内。

用ARMA（5，3）模型预测得到的次日各时间段的时用水量如图5。

图5 时用水量ARMA模型预测结果

ARMA模型预测结果与实测值之间的相对误差分布如图6。相对误差均在±10%之内，且只有个别点误差在±5%之外。

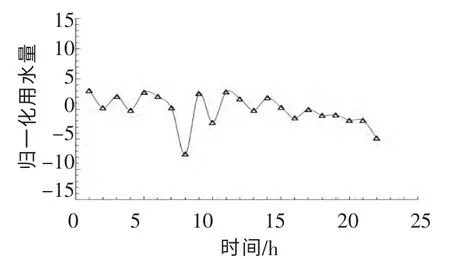
图6 ARMA模型时用水量预测结果的相对误差分布

AR模型及ARMA模型预测结果的均方差MSE和平均绝对百分比误差MAPE如表1。

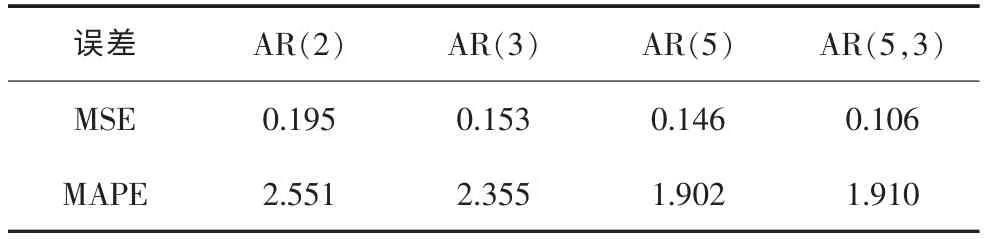
表1 AR和ARMA模型时用水量预测结果 单位：%

由表1可见，ARMA（5，3）模型预测结果的MSE最小，而AR（5）模型预测结果的MAPE最小。

利用17个连续工作日的日用水量，用AR（5）和ARMA（5，3）模型预测得到的后两个工作日的结果如图7。

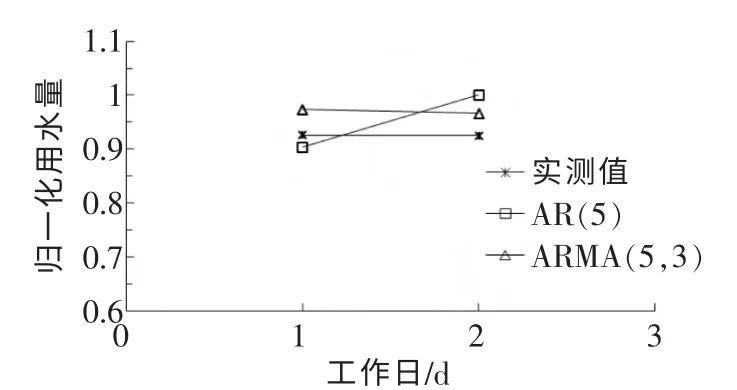
图7 AR和ARMA模型预测结果

预测结果的相对误差如表2，预测结果的相对误差也都在±10%以内。

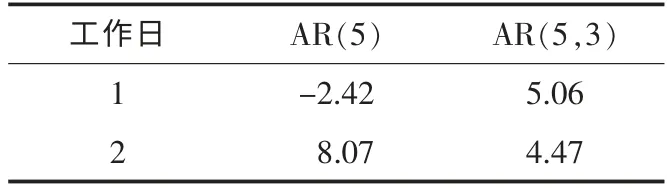
表2 AR和ARMA模型日用水量预测结果的相对误差单位：%

4 结语

（1）用时间序列法中的AR和ARMA模型对某市一区域的时用水量和日用水量进行预测，预测结果与实测值基本一致。与实测值相比，各模型预测结果的相对误差均在±10%以内，且只有个别点的相对误差在±5%之外。

（2）从预测结果的平均平方误差MSE来看，高阶的AR模型要好于低阶的AR模型，ARMA模型要好于AR模型；而从平均绝对百分比误差（MAPE）来看，ARMA模型并不优于高阶的AR模型。

（3）在选择用水量预测模型时，需综合考虑模型的预测精度与模型的复杂程度等因素，以便选取合适的模型进行用水量预测。

［1］JAIN A.，VARSHNEY A.K.，JOSHI U.C.Short-Term Water Demand Forecast Modelling at IIT Kanpur Using Artificial Neural Networks ［J］.Water Resources Management，2001（15）:299-321.

［2］许强.基于神经网络的城市日用水量预测［J］.水科学与工程技术，2012（5）: 58-60.

［3］李红艳，崔建国，张星全.城市用水量预测模型的优选研究［J］.中国给水排水，2004，20（2）: 41-43.

［4］张雅君，刘全胜.需水量预测方法的评析与择优［J］.中国给水排水，2001，17（7）: 27-29.

［5］陈扬.城市时用水量预测模型比较［J］.给水排水工程，2011，29（5）: 71-72.

［6］赵洪宾.给水管网系统理论与分析［M］.北京: 中国建筑工业出版社，2003.

［7］何书元.应用时间序列分析［M］.北京：北京大学出版社，2009.

［8］王黎明，王连，杨楠.应用时间序列分析［M］.上海：复旦大学出版社，2009.

［9］王勇领.预测计算方法［M］.北京：科学出版社，1986.