比例运算电路与加减运算电路教学探究

殷春英，王学军

(衡水学院 电子信息工程学院，河北 衡水 053000)

比例运算和加减运算电路都是以集成运算放大器为核心元件构成的，均设集成运放为理想运放，它们都是通过多个输入信号分别作用于运算放大器的同相输入端和反相输入端，来实现对所输入信号的比例和加减法运算，由其“虚短路”和“虚断路”的特点，再结合节点电流法和叠加原理可以进行各种比例、加减的运算，且外部电阻决定输入信号的比例系数．

但是学生常常受到繁琐的推导和众多的计算公式的困扰，实践证明，如果在一定的条件下，恰当地分析、归纳，充分地利用对称性和统一性，会把繁琐的问题简单化，能进一步提高学生分析问题和解决问题的效率和准确度．

1 比例运算和加、减运算电路的特点分析

比例运算和加、减运算电路中，在运算放大器的输入端常有共模信号成分和输入平均偏置电流及其漂移影响，为使共模输出为零，同时补偿运放输入平均偏置电流及其漂移影响，通常要求运算放大器的输入端电阻平衡，即运算放大器反相输入端和同相输入端所接的电阻相等，也就是说，运算放大器反相输入端和同相输入端所接的电阻具有对称性[1]．

2 基于运算放大器输入端电阻平衡条件下的对称性和统一性分析

基于运算放大器的输入端电阻平衡的特点，我们来分析运算放大器的对称和统一．

2.1 同相比例运算与反相比例运算表达式的对称和统一

2.1.1 同相比例运算和反相比例运算的输入输出电压关系表达式的区别

利用“虚短路”“虚断路”和“节点电流法”可以推导出它们各自的输入电压和输出电压的关系式：

由此可见，反相比例运算电路和同相比例运算电路的输入电压和输出电压的关系表达式不同，从表达式可以看出，它们都与反相输入端的电阻有关．

2.1.2 同相比例运算和反相比例运算[2]输入输出电压表达式的对称和统一

当R′=R// Rf时，即RP= RN， RP为同相输入端的电阻， RN为反相输入端的电阻，即满足集成运放同相输入电阻和反相输入电阻的对称性．下面推导输入输出电阻对称情况下的输入输出电压的关系表达式．

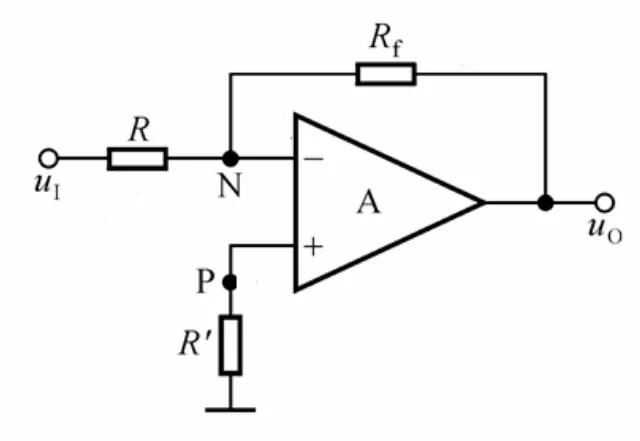
图 1 反相比例运算电路

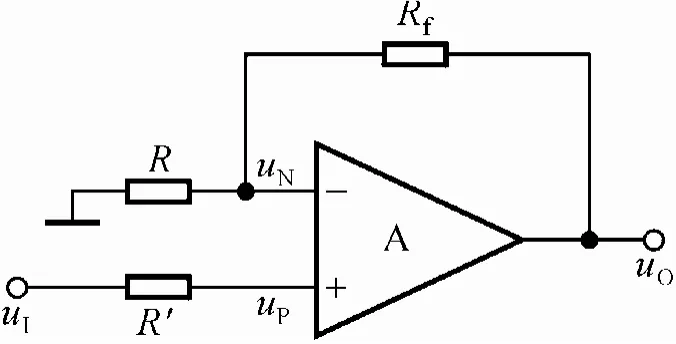
图2 同相比例运算电路

在满足对称的情况下，把R′代入同相比例运算电路得：

由此可见，在满足对称的条件下，同相比例运算和反相比例运算的输入输出电压表达式形式上完全相同，其比例系数均为而只差一个正负号．

总之，对于集成运放来说，在满足对称性的条件下，不论同相比例还是反相比例运算放大，其输出电压总是等于负反馈电阻与输入端输入电阻的比值再乘以输入电压，且同相输入为正，反相输入为负．

2.2 同相求和与反相求和运算表达式的对称性和统一性

2.2.1 同相求和与反相求和运算表达式的区别

利用“虚短路”“虚断路”“节点电流法”和“叠加原理”可以推导出它们各自的输入电压和输出电压的运算表达式：

由反相求和电路(图3)得：

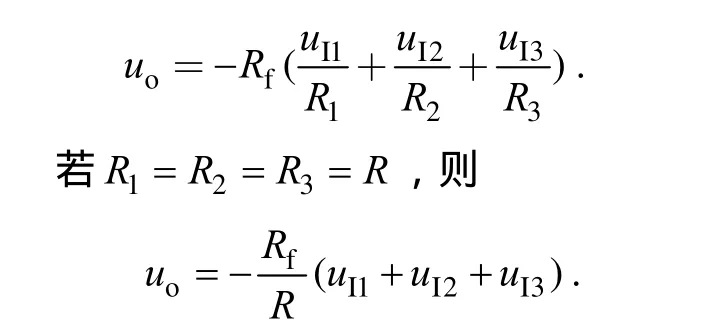
由同相求和电路(图4)知：

同相输入端的电位为：

图 3 反相求和运算电路

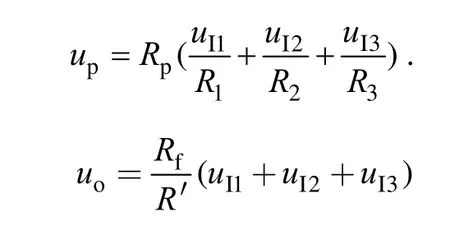
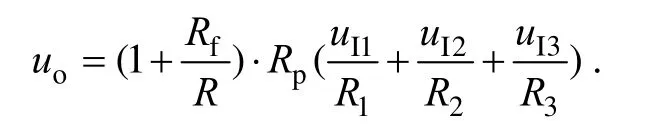
整理得：

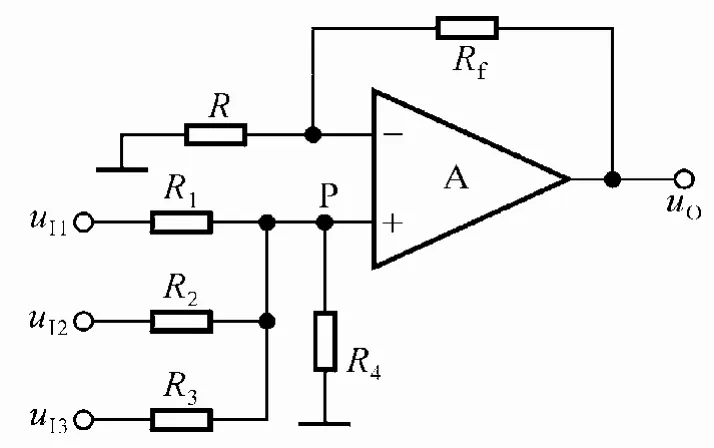
图 4 同相求和运算电路

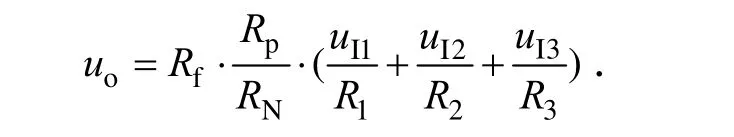
当满足 RP= RN，即满足对称性时(同时满足 R1= R2= R3= R′即各支路输入电阻相等)，则有

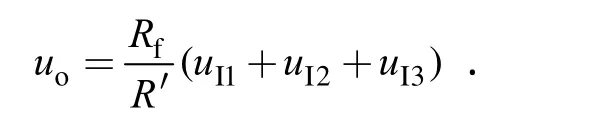
和反相求和相比，表达式的形式一致，只是相差一个正负号．

总之，对于集成运放来说，在满足对称性且 R1= R2= R3的条件下，不论同相求和还是反相求和，其输出电压总是等于负反馈电阻与输入端输入电阻的比值再乘以输入电压，且同相输入为正，反相输入为负．

2.3 求和运算和比例运算的关系

由以上的分析可知，当 RP= RN，即满足对称的关系下，求和运算和比例运算存在一致性.

2.3.1 反相比例运算公式是反相求和运算公式的特例

反相求和时，若只有一路输入，即为反相比例运算，

uo=，与反相比例运算表达式一致．

2.3.2 同相比例运算公式是同相求和运算公式的特例

同相求和时，若只有一路输入，即为同相比例运算，

uo=，与同相比例运算表达式一致．

综上所知，当 RP= RN和R1= R2= R3时，即同相输入端电阻和反相输入端电阻相等，且各输入信号支路电阻也相等时，运算电路的输出电压和输入电压的比例系数为：同相输入端的比例系数为“＋”，反相输入端的比例系数为“－”，其值均为：，即：

3 结语

[1] 华成英,童诗白.模拟电子技术基础[M].北京:高等教育出版社,2006:320-330.

[2] 马敬敏.基于电阻平衡条件的比例运算电路[J].吉林大学学报:信息科学版,2012(2):127-130.