关于复变函数中对数函数的一点讨论
2014-11-23 06:19程凤林
衡水学院学报 2014年1期
程 凤 林
(衡水学院 数学与计算机科学学院,河北 衡水 053000)
在许多复变函数课本中都会涉及初等函数这一节,在复数域上讨论的初等函数与实数域上的初等函数有些性质是一致的,而有一些性质在实数域上成立在复数域上是不成立的,或者有些在实数域上不成立的性质在复数域上却是成立的.关于初等函数中对数函数这一部分,因为复数域上对数函数具有多值性,所以就出现了一些复数域上与实数域上的不同,本文重点讨论这两个式子.这两个式子在实数域上是成立的即而复变函数课本[1-2]上指出两个式子在复数域上一般是不成立的.本文将证明式子在复数域上是成立的,而 L nzn= n Lnz在复数域上则是不成立的.
1 L nz n = n Lnz在复数域上一般不成立
例 1 计算 L n ( 1+i)2=Ln(2i)
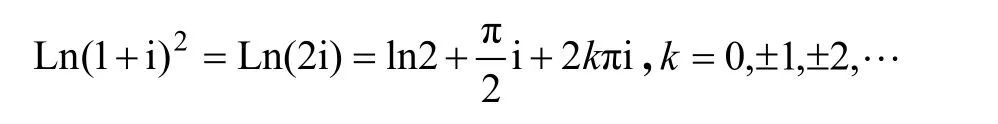
将z设为它的三角结构式:z=r (cosθ +i sinθ),则
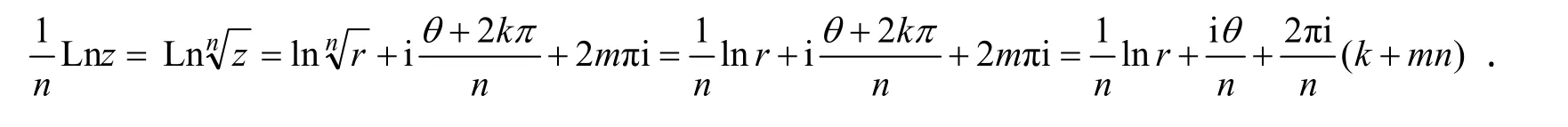
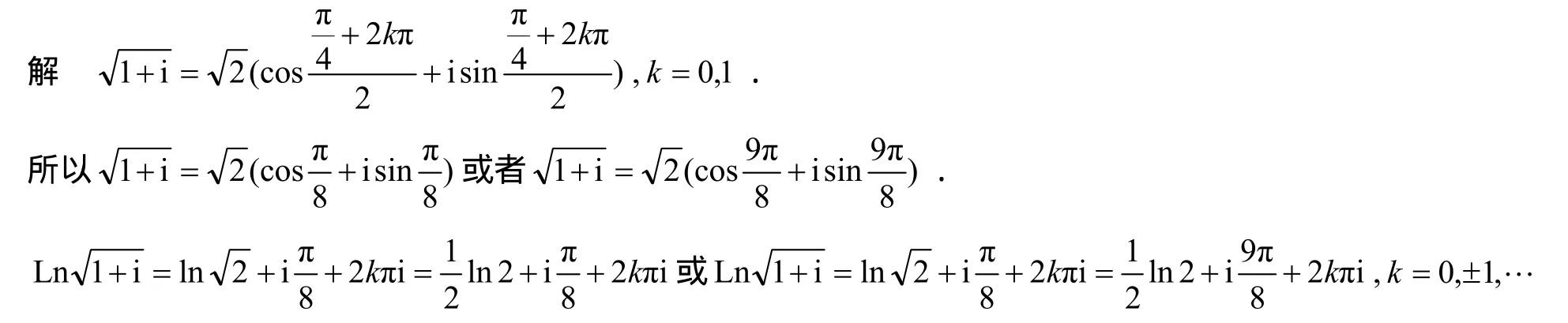
3 结语
本文就关于复变函数与积分变换的很多教材中,复变函数中对数函数这一节中这两个式子是否成立,通过计算发现 L nzn= n Lnz不成立(当n取大于 1的自然数时),而通过计算、讨论发现却是成立的.教材中说这两个式子都是不成立的,因此教材是有出入的,各位主讲复变函数课程的老师应该就这个问题在教学中引起注意.
[1] 刘建亚,吴臻.复变函数与积分变换[M].北京:高等教育出版社,2012:29-31.
[2] 钟玉泉.复变函数论[M].北京:高等教育出版社,2003:69-76.
猜你喜欢
肉类研究(2022年7期)2022-08-05
河北果树(2021年4期)2021-12-02
小猕猴智力画刊(2021年11期)2021-11-28
大众文艺(2020年20期)2020-11-05
青年生活(2020年19期)2020-10-14
河北理科教学研究(2020年1期)2020-07-24
新高考·高二数学(2017年6期)2018-03-29
校园英语·下旬(2017年11期)2017-10-31
校园英语·中旬(2017年9期)2017-09-06
中小企业管理与科技·中旬刊(2009年9期)2009-12-02

