机械润滑在液压伺服比例系统中的应用

唐少楠， 朱小明，2， 杨丽红

（1.上海理工大学 机械工程学院，上海 200093；2.上海豪高机电科技有限公司，上海 201102）

摩擦与振动密切相关，摩擦能够引起振动，振动又会影响摩擦.库仑摩擦力是电液伺服阀和电液比例阀静态特性的主要干扰量，其作用表现为控制元件的稳态和动态特性具有死区和滞环，或表现为动态特性的不稳定因素，这些影响为位置和速度系统的精确控制带来很大的困难［1－2］.且伺服阀阀芯与阀芯腔间的摩擦受泄漏油膜黏度影响，也会增加摩擦阻力，影响控制精度和响应性能［3］.通过在控制信号中叠加高频小幅谐波信号的方法，使阀芯产生微小颤动，来减小阀芯和阀腔接触面的最大摩擦力，以便获得增加伺服阀和比例阀的响应速度，减小伺服比例阀死区，增强系统稳定性的效果，这就是所谓的机械润滑.

1 机械润滑的概念与机理

摩擦有干摩擦、边界摩擦和流体摩擦这3种基本形式，而液压元件主要是边界摩擦和流体摩擦.机械润滑是一种不用通过在摩擦表面添加润滑剂的方法，而是通过对两个相对运动物体之一施加一个高频低幅的颤动，从而使两个物体直接接触表面摩擦力由流体摩擦向边界摩擦转化，以减少接触表面的摩擦力，消除工程中由于库仑摩擦引起的爬行或粘滑现象.

这种颤动可以通过在控制信号中叠加一种小振幅的高频颤振信号实现.根据摩擦颤振补偿的机理和摩擦学理论可知［4］，摩擦副在滑动的过程中，两个粗糙金属表面上的微凸体之间会发生碰撞，各自会受到对方的微脉冲力.尽管各个微脉冲力的大小和方向都是随机的，但是，它们的法向冲力之和能够激发滑块产生不衰减的准周期法向接触振动.这种振动的振幅与滑动速度成正比，频率接近系统的固有频率.上述的振动为非线性，振幅越大，两表面间的距离也会越大，两物体之间的真实接触面积会越小，从而摩擦力也变得越小.基于这种现象，可以利用电子激振器产生颤振信号叠加到线圈的控制电流中，使阀芯作受迫振动.

通常状况下，颤振信号可以叠加在运动法线方向上，但是，大多数是叠加在系统运动的切线方向上.这两者之间的区别是：切线方向的颤振信号主要用于改变摩擦力的大小，而叠加于法线方向的颤振信号主要改变摩擦因数的大小［5］.假设滑块以速度v作垂直于接触面的激振，切向作受迫振动，其运动方程为

式中，yB为切向受迫振动位移；A 为受迫振动的振幅；ω 为受迫振动角频率；t为时间；φ 为受迫振动的初相位.

即时速度

合速度

摩擦力与合速度相反，所以，摩擦力沿着滑动方向的有效分量

化简得到

式中，μ 为动摩擦系数；Fn为正压力.

根据式（3）和式（4）可知，摩擦力f 的有效分量会随着Aω 积的增大而单调地减小，并且由于法向微脉冲力与滑动速度成正比，所以，在切向受迫振动的每个周期内对应的合速度vH出现2次最大值时，法向脉冲力也会出现2次最大脉冲值.若切向激振频率等于法向固有频率一半时，将发生法向接触共振，导致法向振幅最大，摩擦力减少最多［4］.

2 机械润滑在液压伺服比例系统中的应用效果理论分析

图1 死区Fig.1 Dead zone

通过对喷嘴挡板式伺服阀分析来验证机械润滑对伺服阀的影响.伺服阀中的挡板位移x 与滑阀位移y 的关系为［6］

式中，A0为负载液压缸活塞的断面积；q1为流经可变阻尼孔的流量；q2为流经固定阻尼孔的流量；p 为阻尼孔与可变阻尼之间的压力；p0为阻尼孔与可变阻尼之间的初始压力；X 为喷嘴与挡板之间的距离；X0为喷嘴到挡板的初始距离；K 为伺服阀负载的弹性系数；D 为伺服阀负载的阻尼系数；M 为伺服阀负载的质量；f为阀芯与阀芯腔之间的固体摩擦力.

假定添加任意一定值的颤振信号，使挡板产生微小振动，此时，挡板位移为xs，颤振产生挡板的位移为xdsin（ξx＋θ），两者合成挡板的合位移为

式中，xs为给定信号作用下伺服阀挡板的位移；xd为颤振的振幅；ξ为颤振的角频率：θ为颤振的初相位.

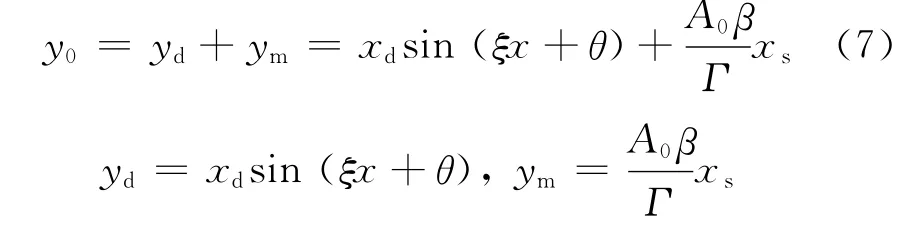
从上述结果可以看出，ym是一个与xs成比例的固定值.如果有足够大的振幅xd使挡板震动，那么，yd就总不为零，从而就可以消除滞环.

另外，通过叠加一定幅值及频率的颤振信号，可以使系统克服粘滑摩擦，使系统在基本恒定的库仑摩擦力的作用下运动，减少系统的滞后时间.

3 机械润滑的颤动电路的设计与调节

由于测量信号不直接驱动比例阀和伺服阀，需要经过放大器放大.同时，为了得到更好的电液伺服阀和比例阀的动静态性能，因此，需要在放大器的控制信号里叠加一个颤振信号来达到机械润滑的目的.颤振信号的波形可以是三角波或正弦波.

图2为三角波颤振电路.图2中，A1为方波发生器，A2为反向积分器，Uin，Uout分别为输入电压和输出电压，R，R1，R2为调节电阻，R01，R02为保护电阻，C 为 电 容，其 频 率最大振幅为为方波电压，Vmax，Vmin分别为最大、最小电压.通过调节R 可以改变颤振信号的频率，调节R2与R1的比值可以改变颤振信号的幅值.

图2 三角波颤振电路Fig.2 Triangle wave dither circuit

图3为正弦波颤振电路.图3中，A1为放大器，R，R1，R2为电阻，C1，C2为电容.R 和C2并联及R和C1串联共同构成选频网络的正反馈，R1及Rf构成选频网络的负反馈，其频率可以通过调节R 来改变频率，可以通过调节电阻Rf来调节幅值［7］.

图3 正弦波颤振电路Fig.3 Sine wave dither circuit

在系统共振频率附近，摩擦力和系统的稳定性会对颤振频率的变化变得非常敏感，为了能平稳调节摩擦力的大小，提高系统运行的稳定性，必须使添加的颤振信号频率避开系统的固有频率［8］，同时还要充分考虑避开伺服阀液压缸的固有频率.考虑到消除极限环和磁滞的作用，一般颤振频率选定在100～200 Hz为宜，大概是3～5 倍控制信号的频率.颤振信号幅值以能消除滞环影响、系统不出现高频抖动为限，颤振信号的幅值一般选为控制信号的10%～20%.

此外，放大器电路中还需要有测量放大电路、阶跃电路和斜坡信号电路、电源电路、报警电路等.其中，测量放大电路用来测量放大处理信号；斜坡信号电路用来将输入的阶跃信号变为一个缓慢上升或下降的连续信号，以便获得平稳而快速的启动、转换或停止；阶跃信号电路用来消除伺服比例阀正反2个方向的死区；电源电路为放大器的正常工作提供能源；报警电路用于指示放大器在工作中的各种可能的错误［9］.

4 机械润滑在伺服比例系统应用的试验探究

为验证机械润滑的应用对伺服比例阀的性能的影响，以海德福斯SP08－47系列比例阀为试验对象搭建3个试验模型——电磁力与位移试验模型、电磁阀响应时间模型和系统稳定性模型，分别验证机械润滑对比例阀响应时间和系统稳定性的影响.

以海德福斯SP08－47系列比例阀线圈搭建一个电磁力－位移试验装置（图4），验证机械润滑对比例阀摩擦力和响应时间的影响.试验时，用电流表观测电磁线圈电路的电流大小，测力传感器末端与阀芯相连，用来记录阀芯受到的推力，LVDT（linear variable differential transformer）位移传感器与阀芯另一端相连，用来记录阀芯的位移.通过在电磁阀线圈控制信号中叠加一个颤振信号的方法来获得机械润滑效果，叠加的颤振信号频率为150 Hz、振幅为控制信号的10%.考虑到叠加颤振后，阀芯移动速度对阀芯上的法向脉冲力和摩擦力的影响，为了更精确地对比叠加颤振后的效果，试验时，通过电机带动阀芯作一个来回匀速往复运动，控制叠加颤振前后两次往复运动的速度相等，并使速度低于动摩擦速度的最小速度，近似于静止运动；用示波器记录下LVDT 位移传感器和测力传感器得到的往复运动的数据，绘制电磁力－位移曲线图，如图5所示.

图4 电磁力－位移测试装置Fig.4 Test device of thrust and displacement

图5 电磁力－位移曲线Fig.5 Thrust and displacement curve

从图5可以看出，由于铁磁材料在加电和失电时存在磁滞现象，以及阀芯和腔体之间存在摩擦力，使得电磁力－位移曲线在阀芯开启和闭合时出现不重合.根据磁滞计算公式，磁滞η＝ΔF／F×100%，ΔF 为电磁力在阀芯开启和闭合的两次差值，F 为阀芯趋于闭合时的电磁力.在比例阀线圈的电流中叠加150Hz的颤振信号后，电磁阀阀芯在工作位置作来回的周期振动，可以减小磁滞和阀芯受到的摩擦力.从测量数据得到，比例阀线圈的电磁磁滞由原来不加颤振的最大值4.9%，减小到叠加颤振后的2.1%，由于摩擦力和磁滞的减小，可以减少比例阀的滞环，提高比例阀的响应时间.

图6为试验装置，由2个颤振频率可调的放大器电路板、比例电磁铁、LVDT 位移传感器、24V 电源、示波器以及信号控制器组成.试验时，调节不同的颤振频率叠加值，通过控制器给线圈施加一个固定的脉冲信号，用LVDT 位移传感器采集阀芯位移传给示波器，数据处理得到阀芯位移曲线，如图7所示（见下页）.由图7可知，叠加颤振信号后，随着颤振频率的增加，阀芯的响应时间会减小，但是，颤振频率超过一定值后，会造成阀芯产生过大的颤振振幅.

图6 比例阀响应时间测试装置Fig.6 Test device of proportional valve response time

为了验证机械润滑对伺服比例系统的影响，按图8（见下页）的原理对SP08－47比例阀搭建比例闭环系统颤振测试试验模型，实物模型如图9所示（见下页）.通过在比例阀控制信号中叠加不同频率的颤振信号的方法，得出闭环系统的时域响应曲线，如图10所示（见下页）.

图7 阀芯在不同颤振下的位移曲线Fig.7 Displacement of valve spool at different dither frequency

图8 比例闭环系统颤振测试的原理图Fig.8 Testing schematic of dither in proportional closed－loop system

图9 比例闭环系统颤振试验装置Fig.9 Test device of dither in proportional closed－loop system

从图10可以看出，在没有叠加颤振信号时，由于摩擦力的存在，在系统时域曲线出现极限环震荡；但是，当在控制信号中叠加150 Hz的颤振时，极限环震荡消失，曲线趋于稳定；当叠加40 Hz 和350Hz的颤振时，时域曲线产生极限环震荡，前者是由于叠加的颤振频率和系统的固有频率相近造成的系统共振，后者是由于过大的颤振频率造成阀芯颤振幅度过大，从而使系统产生极限不稳定状态.由于比例阀和伺服阀结构和控制的相似性，因此，通过机械润滑的方法也可以减小伺服系统的电磁磁滞和响应时间，增强系统的稳定性，但是，其叠加的颤振频率必须避开系统的固有频率.

图10 不同频率颤振下的系统时域曲线Fig.10 Time domain curve at different dither frequency

5 结束语

通过机械润滑原理的理论分析以及在比例阀控制信号中叠加颤振信号前后效果的对比，很好地证明了机械润滑可以将伺服比例阀阀芯的静摩擦力转变为动摩擦力，使得最大静摩擦力减小，从而可以使系统的粘滑运动转化为平稳运动，消除摩擦滞环和磁滞现象，因此，机械润滑能够很好地改善系统的稳定性和响应时间，增强伺服比例控制系统的速度和位置控制品质.

［1］路甬祥，胡大纮.电液比例控制技术［M］.北京：机械工业出版社，1988.

［2］Ender D B.Implementation of deadband reset scheduling for the elimination of stick－slip cycling in control valves［J］.Journal A，1997，38（1）：11－15.

［3］张春平，唐大伟，曲伟，等，粗糙度对微细通道内流动特性影响的实验研究［J］.上海理工大学学报，2008，30（1）：55－58.

［4］陆大雄.摩擦学导论［M］.北京：北京出版社，1990.

［5］孔祥臻，王勇，蒋守勇.基于Stribeck模型的摩擦颤振补偿［J］.机械工程学报，2010，46（5）：68－73.

［6］池辺洋，池辺润.电液伺服机构及元件［M］.北京：高等教育出版社，1982.

［7］童诗白，朱成英，模拟电子技术基础［M］.3 版.北京：高等教育出版社，2003.

［8］Hagglund T.A friction compensator for pneumatic control valve［J］.Journal of Process Control，2002，8（12）：97－99.

［9］杨征瑞，花克勤，徐轶，等.电液比例与伺服控制［M］.北京：冶金工业出版社，2009.