共享历史最优信息搜索的粒子群算法

连志刚， 曹 宇， 林蔚天， 计春雷

（上海电机学院 电子信息工程学院，上海 201306）

粒子群算法思想来自鸟群或者鱼群的觅食行为，通过个体间特殊的信息传递方式，使整个团体朝同一个方向逼近，从而搜索到最终目标.粒子群算法的思想就是源自此类群体行为理论.该算法由心理学博士Kennedy和电气工程师Eberhart提出，通过群体中个体之间的协作和信息共享来寻找最优解［1－2］.

粒子群算法是一种群优化技术和群搜索算法，它通过群体的合作，进行高效搜索.正如文献［3］所说，社会行为有两个主要目的：一是每个个体能够在搜索食物的过程中协助其它群内的成员；二是群体合作能够提高搜索效率.粒子群可以认为是粒子在搜索空间里，按一定传递规律传递信息，并根据信息变化改变自己的搜索方向.传统粒子群算法搜索信息主要来自于两方面：一是群体最优位置；二是粒子自身经验最优位置.群体最优位置使得粒子能够快速收敛，并对全局极值的邻域进行搜索；个体自身经验最优位置保证粒子不至于过快收敛到群体最优而陷入局部最优，使得粒子能够在一次迭代中对个体极值和全局极值之间的区域进行搜索［4］.不同的优化问题需要很好的平衡局部和全局的比例关系.文献［5］提出Iemetic粒子群优化算法，利用一种新的specie构造方法来保证其能够发现不同最优解所在的搜索区域，通过一种适应性的局域搜索算子增强specie追踪到最优解的能力，重新初始化策略来进一步改善算法在动态多峰环境中的性能.文献［6－7］对PSO（particle swarm optimization）在全局优化、装载平衡等方面进行了研究.关于PSO 的应用研究报道较为丰富，如文献［8］提出一种粒子群与人工免疫学习结合的混合算法解决固定收费运输问题.Hamta等在文献［9］中提出了一种混合PSO 算法优化装配线平衡的多目标问题.文献［10］提出一种有效的二进制PSO 算法优化多目标资源分配问题.文献［11］应用粒子群算法解决工程项目多目标执行模式优化问题.作者［12－13］研究了共享每代种群中粒子最好位置信息，以及结合局部与全局最优的改进型粒子群算法，文献［14］仿真证明其效率较高.

本文提出一种共享历史最优信息搜索的粒子群算法，它除了共享个体和全局粒子良好信息外，还共享了前次运行时的种群中个体粒子历史最优信息，并将该算法应用于一些典型非线性测试函数的优化，实验结果表明了它的有效性.

1 基本粒子群算法

粒子群算法中的每个粒子都是D 维解空间的一点，具有速度和位置，但没有质量和体积.空间中的某个粒子的位置表示为xi＝（xi1，xi2，…，xiD），i＝1，2，…，m，速度为vi＝（vi1，vi2，…，viD）.它所经历过的最好历史位置为pi＝（pi1，pi2，…，piD）；它能共享的群体的最好位置以索引g表示，记为pg.每个粒子将根据自身飞行经验和群体飞行经验来调整自己的飞行轨迹，根据以下公式更新自己的速度和位置.

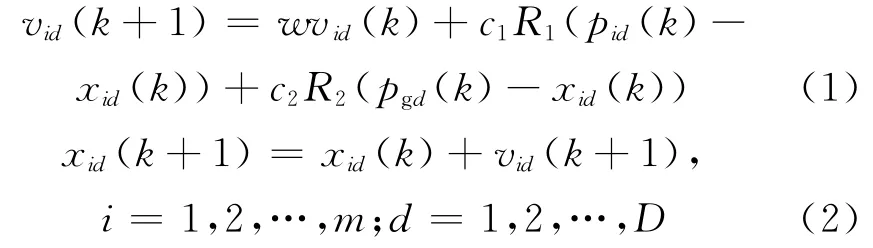
式中，w 为惯性权重；学习因子c1和c2为正常数；k为迭代次数；R1，R2为分布在［0，1］上的随机数；vid（k）为每一个粒子在第d 维的速度；xid（k）是粒子当前位置；pid（k）是每个粒子到目前为止所出现的最优位置；pgd（k）为所有粒子到目前为止所出现的最优位置.

式（1）中，第一部分称为惯性部分，由粒子先前的速度引起；第二部分为自我认知部分，代表粒子本身的思考；第三部分为社会认知部分，表达粒子之间的协作以及粒子对群体共有信息的认可程度.以上3部分共同影响粒子速度和位置的更新.粒子的自我认知部分体现了粒子对自身经验的积累，粒子的社会认知部分体现了粒子之间的信息传递.

基本PSO 算法在进化过程中除跟踪自身最优外，只与种群最优粒子发生信息交流.在进化过程中，种群最优对其影响很大，一旦粒子赶上种群最优，粒子会聚集到相同位置并停止，从而导致算法过早收敛而出现早熟［15］.因而，本文提出一种结合前次运行时的历史最优信息的改进型粒子群算法.该算法的粒子在位置更新时除共享自身最优和种群最优外，还将参考算法前次运行搜索到的粒子历史最优信息，从而克服算法过早收敛而出现的早熟问题.

2 共享历史最优信息的粒子群算法

基于PSO 算法的特性，本文提出共享历史最优信息搜索的粒子群算法SHOIPSO（share historical optimal information particle swarm optimization algorithm），将其多次运行搜索到的历史最优点信息共享于下一次算法的搜索.这种算法模型在一定程度上充分共享、继承了PSO 算法前次运行的历史最优点信息、本次运行的历史最优点信息、本次运行获得的全局最优信息，其共享的信息具有多样性，搜索能力及效率将会更好.算法假设如下.

假设在一个D 维的目标搜索空间中，有m个粒子组成一个种群，其中第i个粒子表示为一个D 维的向量xi＝（xi1，xi2，…，xiD），i＝1，2，…，m，即第i个粒子在D 维的搜索空间中的位置是xi.vi＝（vi1，vi2，…，viD）是第i个粒子的飞行速度；pi＝（pi1，pi2，…，piD）是第i个粒子迄今为止搜索到的最优位置pbest；pg＝（pg1，pg2，…，pgD）是整个粒子群迄今为止搜索到的最 优 位 置gbest；PH（t）＝（pt1，pt2，…，ptD）是该算法运行第t次种群搜索到的个体历史最优位置hbest.SHOIPSO 算法的迭代公式为

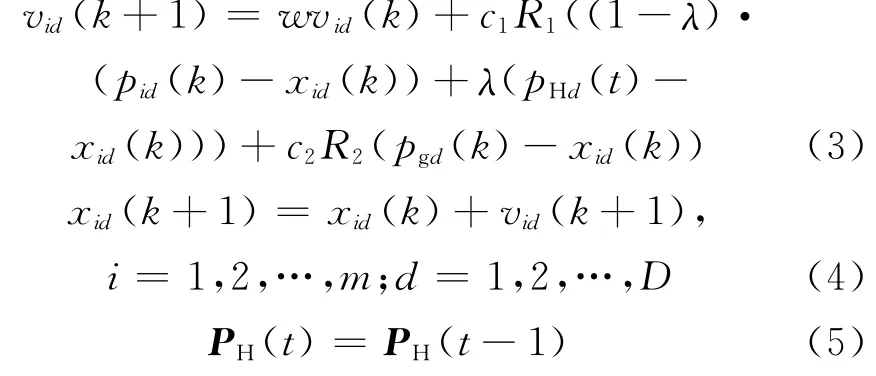
式中，k，w，R1，R2，c1，c2，vid（k），xid（k），pid（k），pgd（k）与SPSO 表示的意义相同.t表示该算法的运行次数，一般运行10 次.λ 为在［0，1］之间的一个常数，表示共享继承历史最优信息的程度.λ越大说明共享继承的力度越大，但容易陷入历史最优，具体取多大算法的效率最好，有待数据模拟实验验证.当SHOIPSO 算法运行第1 次的时候，因为前次没有历史 最 优 信 息 可 供 继 承，故λ 取0.pHd（t）是SHOIPSO 算法运行第t次时，种群中个体粒子搜索到的历史最优点的第d 维分量.迭代终止条件根据具体问题一般选为最大迭代次数或（和）粒子群迄今为止搜索到的最优位置满足预定最小适应阈值.

SHOIPSO 算法可以扩展为随机共享历史最优信息搜索的粒子群算法RSHOIPSO（random share historical optimal information particle swarm optimization algorithm），两者的区别为，式（5）变为

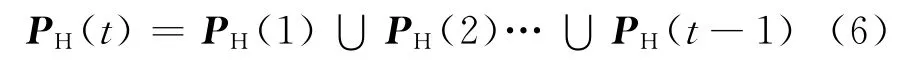
PH由RSHOIPSO 算法运行第1次时到第t－1次时的种群个体历史最优信息按比例构成，其相互间比例为多大时算法效率最高，还有待模拟实验分析.

SHOIPSO 算法和RSHOIPSO 算法迭代公式主要通过4部分来更新粒子i的新速度：粒子i前一次迭代时刻的速度；粒子i当前位置与自己最好位置之间的距离；第t次运行搜索到的历史最优位置与自己位置之间的距离；同时再结合粒子i当前位置与群体最好位置之间的距离.该算法的特点是将历史最优粒子和种群最优粒子进行结合，最大限度地共享继承了历史最优信息.

3 SHOIPSO 算法的函数优化仿真实验

为了验证SHOIPSO 算法的优化效果，下面给出5个经典的测试函数，并和基本PSO 算法测试比较，分析其优化性能.

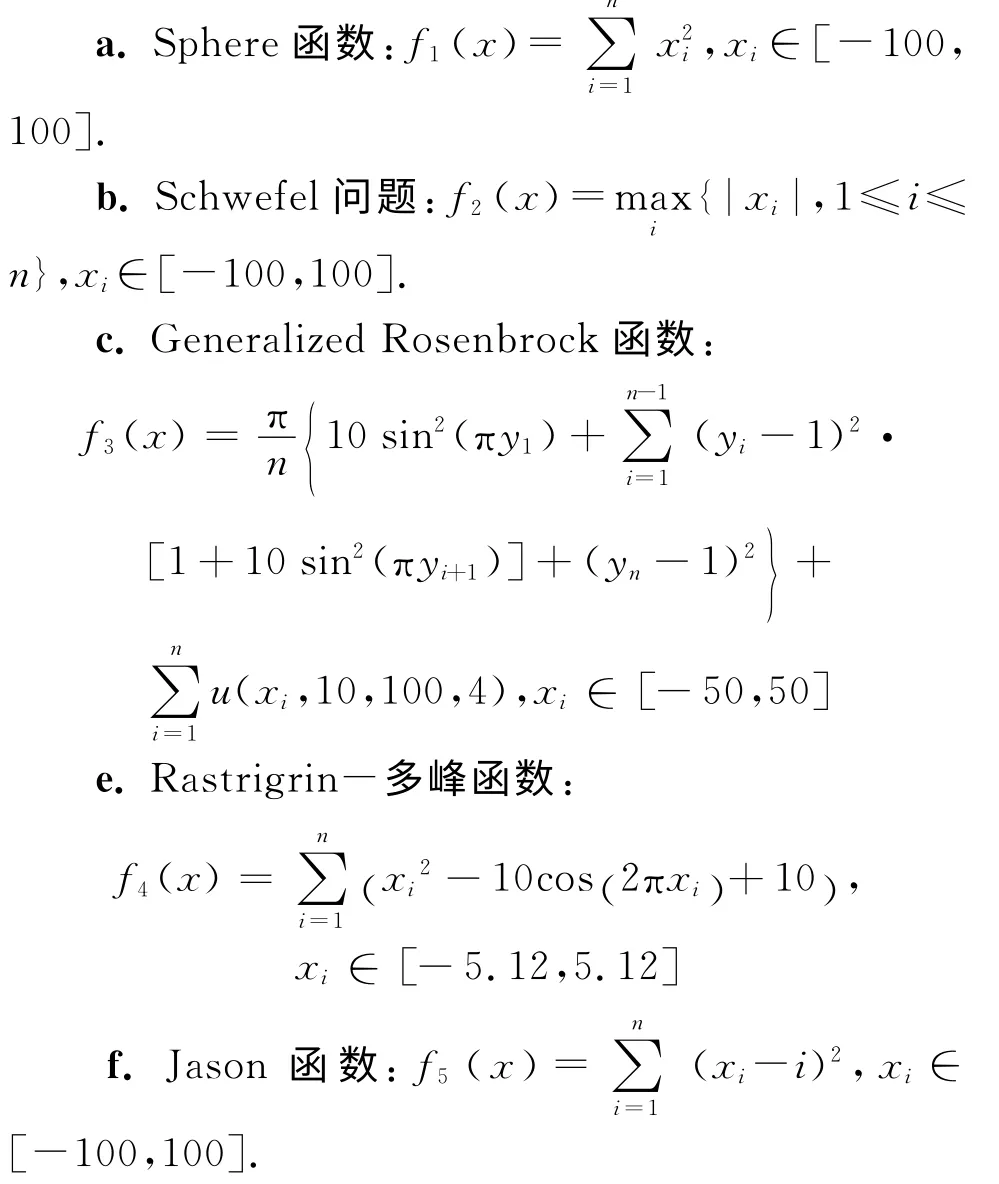
在测试比较过程中，两种算法在每一轮比赛中取完全相同的参数，这样才能体现出不同算法所产生的效果.分别对每个目标函数运行10次，再从这10次结果中求出最小值（min）、最大值（max）和平均值（average）.本文将优化结果的主要数据抽取出来，列在表1 中.另外，为了作图方便，每运行一次SHOIPSO 和RSHOIPSO 算 法，基 本PSO 也 运 行一次进行对照（虽然其参数没有改变）.SHOIPSO，RSHOIPSO，OPSO 算法搜索最优解过程中最优收敛性能曲线如图1所示。

表1中，f 指经典的测试函数；D 为该函数的维数；Ps和G 分别为算法的种群规模和停止迭代的代数；Best 表示该函数的理论最优值.对于RSHOIPSO 算法，本文模拟实验采用将第t－1 次运行的历史最优按照比例p 插入前面的PH（t－2），为了避免论文数据过多、篇幅过大，本文的比例参数取p＝Ps／10和p＝Ps／5进行实验分析.

将3种算法的仿真结果进行比较，最优的那个值标记为黑体.它对应的算法代表意义是：在优化某个函数时，这种算法效果在3种算法中是最好的.它对应参数的意义是：在优化此函数时，在这种算法各种参数组合中，这组参数的组合效率是最好的.这组参数将为此算法将来的应用提供指导意义.

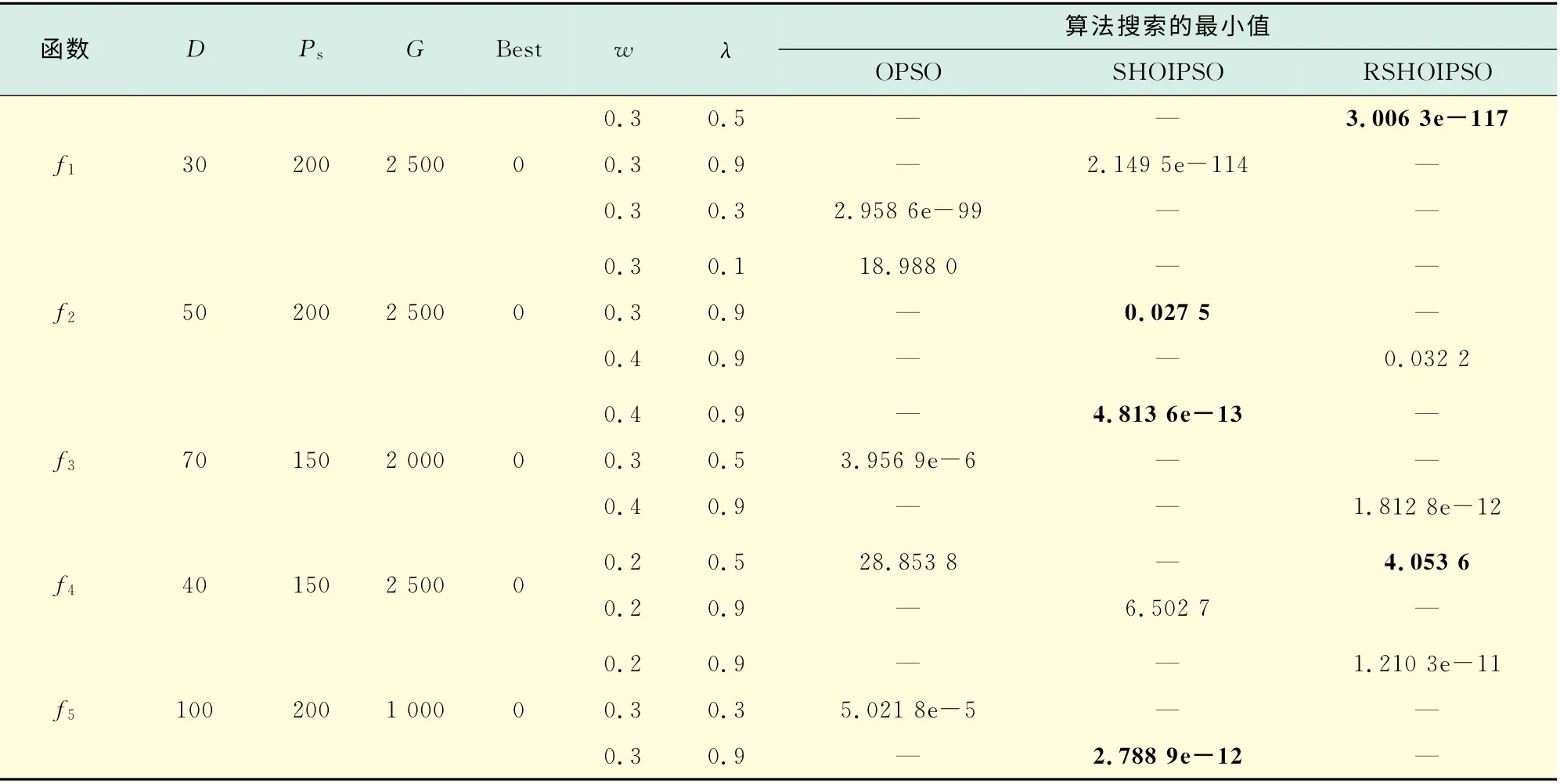
表1 OPSO，SHOIPSO，RSHOIPSO 算法优化函数的比较Tab.1 Comparisons between optimization functions of OPSO，SHOIPSO and RSHOIPSO algorithms

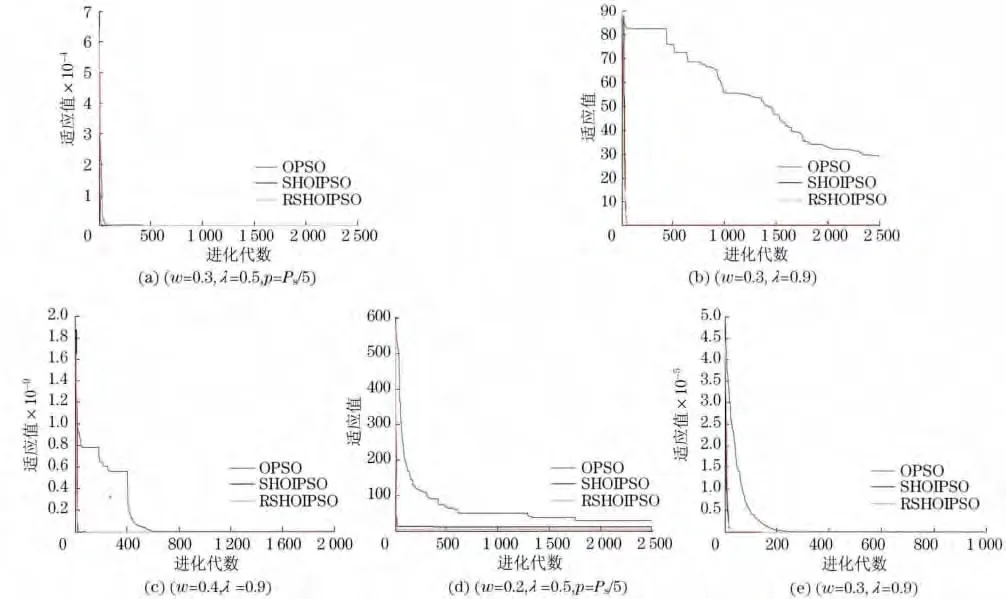
图1 SHOIPSO，RSHOIPSO 与OPSO 算法优化函数的收敛比较Fig.1 Comparisons between convergence figures of SHOIPSO，RSHOIPSO and OPSO algorithms

从仿真数据可以看出，SHOIPSO 和RSHOIPSO算法在收敛精度上取得了明显的效果，它们的优化精度要比OPSO算法高出至少几个数量级.从表1可以看到，λ分布在（0.5，0.9）之间时，5个函数全部取得最优值.因此，作者建议以后进行函数优化时，可以将λ值只设置在（0.5，0.9）范围内，这样可以大大提高优化效率.特别是权重系数w 在取0.3和0.4时搜索性能相对较强.因此，算法参数设置时，w 一般取0.3和0.4.对于优化函数f1和f4，RSHOIPSO的效果都优于其它两种算法，其p 值都为Ps／5，即第t次的种群个体历史最优按Ps／5插入第t－1次的种群个体历史最优.

从仿真图来看，SHOIPSO，RSHOIPSO 收敛性能较OPSO 算法明显好，且收敛精度高.特别从优化函数f2和f4的仿真图可以看出，该文提出的算法很快跳出了局部最优且收敛速度快.从仿真数据和收敛图可验证，本文提出的共享历史搜索最优信息策略是有效的，提高了算法搜索解的多样性，跳出了局部最优.故本文提出的新型PSO 算法搜索性能较强，可以作为一种解决高维非线性复杂问题的优化工具.

4 结 论

本文提出了一种共享历史最优信息搜索的粒子群算法.仿真结果表明该改进型算法在优化函数时，其收敛效果与收敛速度都有较大提高.本文的意义在于指出了粒子在搜索过程中不仅共享个体和全局粒子良好信息外，还共享了算法前次运行获得的历史最优信息的思路，为粒子群的搜索扩大了范围，减小了粒子群搜索陷入局部最优解的欠缺.所以，可以作为一种改进粒子群算法的新思路.另外，本文还通过实验仿真，给出了对于一般函数优化时参考的λ和w 的取值范围，为改进算法SHOIPSO 的应用提供了参考信息.

本文给出了粒子搜索过程中共享历史最优粒子的两种不同方式.然而在函数f4优化过程中，虽然新算法收敛效果比传统PSO 算法好，但是最终仍然陷入局部最优.所以，可以对共享历史最优信息的方式以及参数设置作进一步研究和讨论.

［1］Kennedy J，Eberhart R.Particle swarm optimization［C］∥Proceedings of IEEE International Conference on Neural Networks.Portland：IEEE，2003.

［2］Eberhart R，Kennedy J.A new optimizer using particle swarm theory［C］∥Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Nagoya：IEEE，1995.

［3］Beekman M，Ratnieks F L W.Long－rang foraging by the honey－bee［J］.Functional Ecology，2000，14（4）：490－496.

［4］王存睿，段晓东，刘向东，等.改进的基本粒子群优化算法［J］.计算机工程，2004，30（21）：35－37.

［5］王洪峰，王娜，汪定伟.一种求解动态多峰优化问题的Memetic粒子群算法［J］.系统工程理论与实践，2013，33（6）：1577－1586.

［6］Ghodrati A，Lotfi S.A hybrid CS／PSO algorithm for global optimization［J］.Intelligent Information and Database Systems，2012，7198（2）：89－98.

［7］Liu Z H，Wang X L.A PSO－based algorithm for load balancing in virtual machines of cloud computing environment［J］.Advances in Swarm Intelligence，2012，7331（4）：142－147.

［8］El－Sherbiny M M，Alhamali R M.A hybrid particle swarm algorithm with artificial immune learning for solving the fixed charge transportation problem［J］.Computers ＆Industrial Engineering，2013，64（2）：610－620.

［9］Hamta N，FatemiGhomi S M T，Jolai F，et al.A hybrid PSO algorithm for a multi－objective assembly line balancing problem with flexible operation times，sequence－dependent setup times and learning effect［J］.International Journal of Production Economics，2013，141（1）：99－111.

［10］Fan K，You W J，Li Y Y.An effective modified binary particle swarm optimization algorithm for multiobjective resource allocation problem［J］.Applied Mathematics and Computation，2013，221（3）：257－267.

［11］周蓉，叶春明.基于粒子群的多目标多执行模式项目调度［J］.上海理工大学学报，2013，35（1）：27－32.

［12］Lian Z G.A local and global search combine particle swarm optimization algorithm for job－shop scheduling to minimize makespan［J］.Discrete Dynamics in Nature and Society，2010，2010：1－12.

［13］闫雪丽，王学武，连志刚.结合历史全局最优与局部最优的粒子群算法［J］.华东理工大学学报，2011，37（4）：515－520.

［14］胡乃平，宋世芳.一种局部与全局相结合的微粒群优化算法［J］.计算机工程，2008，34（17）：20－27.

［15］蔡昌新，张顶学.带邻近粒子信息的粒子群算法［J］.计算机工程与应用，2009，45（18）：40－42.

［16］唐柱，丁学明，刘灿.基于引力搜索和粒子群混合优化算法的T－S模型辨识［J］.上海理工大学学报，2013，35（4）：351－354.

［17］柳寅，马良，黄钰.基于模糊粒子群算法的非线性函数优化［J］.上海理工大学学报，2012，34（4）：314－317.