大口径火炮弹丸挤进过程坡膛动力响应分析

马明迪，崔万善，曾志银，宁变芳，李宗贤，张薇薇

（西北机电工程研究所，陕西 咸阳 712099）

弹丸挤进过程是一个非常复杂的非线性力学过程，其涉及了材料、几何和边界条件等多个非线性问题，如弹丸与身管内膛的冲击摩擦，弹带的大变形等，且整个过程历时极短，难以用实验进行准确观察和测量，也无法通过常规的理论计算进行准确合理的描述［1］.而对于弹丸挤进过程的研究，是探究内弹道峰值出现机理，界定弹带与内膛的磨损关系，分析阳线损伤机理等方面问题不可或缺的前期工作，具有重要的现实意义［2］.因此，弹丸挤进过程的数值模拟越来越受到重视.

目前，国内外在此方面的研究报道并不多见.文献［2］利用Dytran软件模拟了火炮弹带挤进过程，分析了挤进过程中弹带、身管和膛线的应力状态及变化规律，模型中做了一定的简化.文献［3］利用ANSYS软件，建立了一个较为简单的模型，进行了弹带挤进应力及变形分析.文献［4］对弹丸模拟试验中弹丸挤进过程中产生的变形问题进行了动力学建模；改变弹头壳的厚度，对弹丸在挤进过程中的变形和热量分布进行了有限元分析.文献［5］建立了弹带挤进、冲击坡膛的显式有限元模型，对在两种不同结构坡膛条件下的弹带挤进过程进行了分析计算，得到了挤进过程中弹丸及弹带的动力学响应.文献［6］建立了弹丸挤进枪管的有限元分析模型，通过数值模拟研究了铅芯弹丸的挤进过程，分析了挤进前后弹头壳和铅芯的变形特征.

本文在汲取前人研究经验的基础上，基于弹塑性有限元接触理论，建立了大口径火炮的弹丸身管耦合系统显式非线性有限元模型.考虑到初始装填角、弹炮间隙、弹丸装填不到位等因素，对弹丸挤进过程中坡膛的动力响应进行了详细分析，并在此基础上针对火炮实弹射击中出现的阳线损伤问题进行了深入探讨.

1 计算模型

本文以大口径火炮弹丸身管耦合系统为研究对象，计算模型包括身管、弹带和弹体.

身管模型中除膛线起始阶段和径向过渡单元采用棱柱单元外，其他部位全部采用六面体单元.将身管沿轴线切分出一根膛线，并进行拓扑处理，将身管模型分割成若干个简单、可映射的部分.从膛线起始部分开始进行网格划分，采取分段扫描拉伸的方式，沿着膛线空间曲线进行扫描，得到单根膛线有限元模型.最后将单根膛线进行旋转以及合并结点处理，得到身管有限元模型，如图1 所示.

图1 身管有限元模型Fig.1 FE model of barrel

由于膛线存在一定缠度，因此弹带被阳线刻出的沟槽也带有一定角度，为了减小网格的畸变，在处理弹带网格时使其保持与膛线初始缠角相同的角度.为了提高弹带变形的模拟精度，在弹带处布置的网格为高质量的小尺寸网格，网格最小边长均在0.5mm 左右.

图2 为弹丸有限元模型，图3 为弹带处网格细节图.

图2 弹丸有限元模型Fig.2 FE model of projectile

图3 弹带处网格Fig.3 Mesh of bearing band

2 材料模型

身管为炮钢材料，采用双线性模型.

弹带为H96 黄铜，采用Johnson-Cook 模型.这种材料模型也可以称为粘塑性模型，是描述材料在大变形、高应变率和高温条件下的本构模型，适用范围广泛，包含大部分金属材料［7］.

Johnson-Cook 模型的流动应力表达式为

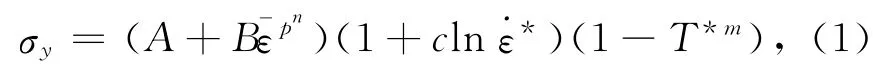
式中：A，B，c，n，m为材料常数；为等效塑性应变；为等效塑性应变率；T＊＝（TTroom）／（Tmelt-Troom）为相对温度.

采用Gruneisen 状态方程

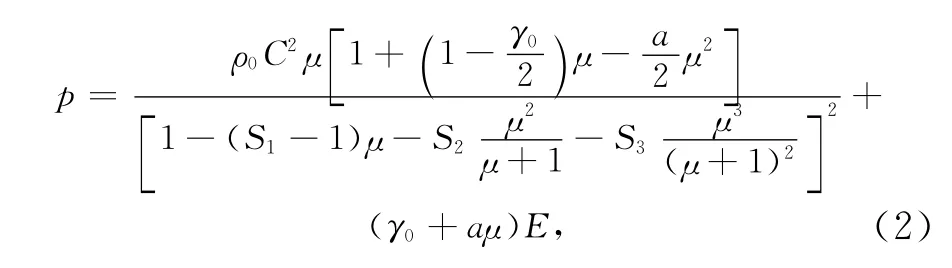
式中：ρ0为初始密度；E为内能；μ＝ρ／ρ0-1，ρ为当前密度；C为材料内冲击波速度-质点速度曲线的截距；S1，S2和S3为冲击波速度-质点速度曲线的斜率的系数；γ0为Gruneisen伽马；a为对γ0一阶体积修正.

在挤进过程中要重点关注弹带与身管之间的作用过程，为提高计算效率，弹体简化为刚体.

3 接触算法

本文模型中共有3个接触对：

1）接触-碰撞模型.弹带与身管内表面的接触-碰撞，弹体与身管内表面的接触-碰撞.

以弹带与身管内表面接触-碰撞模型为例，将弹带结点定义为从结点，将身管内表面定义为主表面.采用罚函数法，每一时间步检查弹带从结点是否穿透主表面，没有穿透不做任何处理，否则在该从结点与被穿透的主表面间引入一个大小与穿透量及主表面单元刚度成正比的接触力.这种处理方法相当于在从结点和被穿透的主表面之间设置一个法向弹簧，以限制从结点对主表面的穿透［8］.

2）固连接触模型.弹带与弹体的固连接触.

将弹带结点定义为从结点，将与弹带相接触的界面上的弹体单元表面定义为主表面，仅约束弹带从结点的平动自由度.如果弹带从结点与对应的主表面存在微小的距离，则采用正交投影的方法将从结点移动到主表面上.在每一个时间步中，首先将每一个从结点的质量和结点力分配到该从结点接触点的主片各结点上，然后计算各主结点的加速度.从节点的加速度可以由包含其接触点的主片各结点加速度插值得到［9］.

4 数值模拟及结果分析

本文研究了大口径火炮弹丸挤进过程中坡膛的动力响应规律.

模型采用0号装药，根据内弹道计算所提供的弹底压力-时间曲线，施加弹底压力，以模拟火药气体对弹丸的冲击作用，弹底压力-时间曲线如图4 所示.

本文建立的力学模型做如下假设：

1）根据设计所提供的弹底压力-时间曲线施加弹底压力，以模拟火药气体对弹丸的冲击作用；

2）将复进机、驻退机、摇架对身管的作用简化为身管尾端面的固定约束；

3）由于挤进部位距身管约束端很近，且挤进过程历时极短，故不考虑身管和弹丸的自重影响；

4）考虑定心部间隙造成的炮膛轴线与弹轴不重合的初始状态.

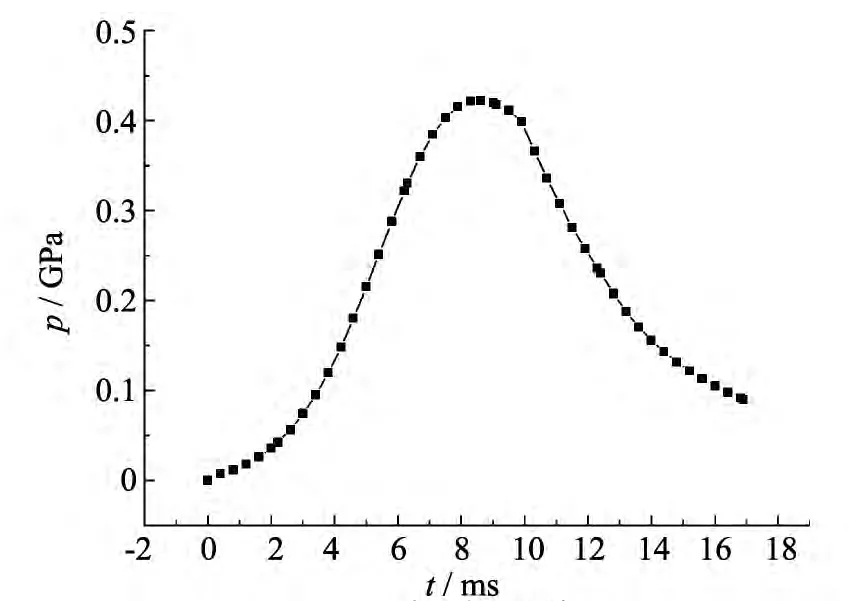
图4 压力-时间曲线Fig.4 Curves of pressure-time

本文对以下4种工况进行了模拟：

1）身管阳线与弹丸定心部间隙为0.02mm，弹丸轴线与身管轴线重合；

2）弹管间隙为0.02mm，弹丸初始装填角取为0.4′；

3）弹管间隙增大到0.22mm，弹丸轴线与身管轴线重合；

4）弹管间隙为0.02mm，弹丸与身管轴线重合，弹丸装填不到位.

4.1 坡膛应力分析

图5为工况1不同时刻坡膛等效应力分布图.由图中可以看出，随着弹丸的挤入，在坡膛内形成一系列的等效应力带，阳线部分的应力要远大于阴线.在1.5ms左右，前弹带开始刻槽，与弹带接触的阳线出现明显的应力集中，最大等效应力在500 MPa左右.随着弹丸的继续挤进，坡膛应力逐渐增大，在3ms 左右弹丸挤进基本完成，坡膛和导向部过渡段应力集中严重，接近身管材料屈服极限.这是因为在此处附近弹带挤进过程的变形达到最大，因此对应的弹带变形阻力和摩擦力均达到最大.在实际使用的情况中，坡膛和导向部的过渡段也是膛线磨损和损伤的多发位置.

为了便于分析弹丸挤进过程中坡膛表面不同部位的应力变化情况，在阳线表面导转侧沿轴线方向取6个单元，如图6所示.1号单元位于膛线起始处前面部位；2 号单元位于弹带开始切入膛线部位，即膛线起始点处；3号单元和4号单元位于2号单元和5号单元之间；5号单元位于坡膛结束、直膛段开始位置；6号单元位于直膛段.

图5 工况1坡膛等效应力分布图（单位：GPa）Fig.5 Distribution map of equivalent stress of chamber throat in operating mode 1

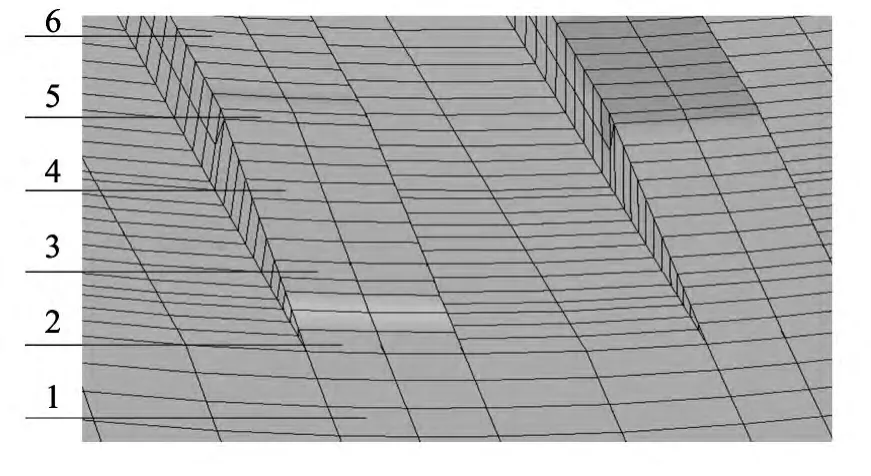
图6 坡膛表面选取单元分布图Fig.6 Distribution of selected elements on chamber throat surface

1）径向应力分析.图7为工况1时身管1到6 号单元径向应力随时间变化的曲线.从图中可以看出，除1 号单元外，各分析点的径向应力变化趋势基本相同，曲线有两个峰值，分别对应前弹带和后弹带与阳线相接触.1 号单元与前弹带作用不明显，因此只出现了一个峰值.各单元径向应力峰值出现的先后顺序与其编号一致.由于弹带在挤进阶段的变形逐渐增大，3 到5 号单元的两个应力峰值均呈增大的趋势；在坡膛和直膛段过渡段位置处，由于弹带变形量达到最大，因此弹带与阳线的相互作用达到最大，应力集中严重.而6 号单元已进入导向部，出现了一定的卸载现象，因此应力峰值略小于5 号单元.

2）轴向应力分析.在弹丸挤进的过程中，坡膛表面不仅有径向应力，而且还有轴向应力.比较各分析点的轴向应力和径向应力曲线（图8 和图7），可以看出两种应力随时间变化的规律基本相同，但轴向应力要小于径向应力.

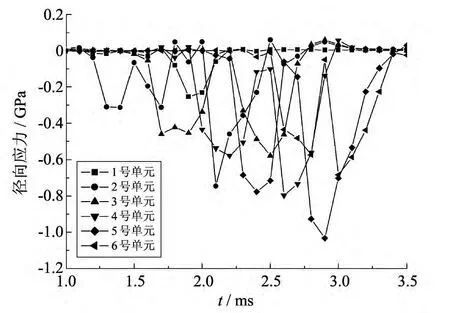
图7 工况1各选取单元径向应力变化曲线Fig.7 Changing curves of radial stress of selected elements in operating mode 1

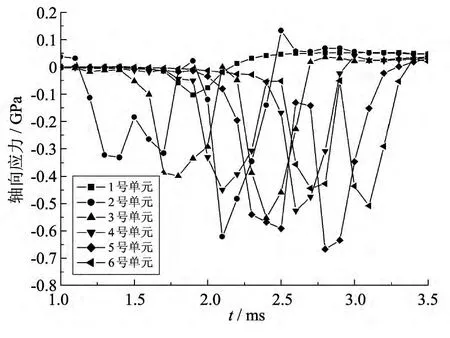
图8 工况1各选取单元轴向应力变化曲线Fig.8 Changing curves of axial stress of selected elements in operating mode 1

3）坡膛磨损分析.坡膛表面的正应力主要由径向应力和轴向应力组成.由径向应力和轴向应力的分析可知，阳线表面的正应力最大值在5号单元附近，即坡膛与直膛段过渡处.由于摩擦力与正压力之间存在正比关系，因此导向部起始处附近弹带与身管阳线的摩擦力达到最大，相应的磨损量也最大，这与火炮实际的使用情况相吻合.

4）各工况下单元等效应力.图9 为各工况下身管阳线1到6号单元等效应力变化曲线.由图中可以看出，初始装填角和装填不到位对身管应力水平影响不大.工况3的波峰比其它工况靠前，应力水平普遍较低.这是由于随着弹炮间隙的增大，弹带与身管内表面的过盈量逐渐减小，身管与弹带的相互作用减小，弹丸运动阻力减小，弹丸运动速度增大.工况4的波峰与工况1到来的时刻无明显区别，但是由于装填不到位，工况4弹丸的行程增大，因此可以看出工况4弹丸的速度相对较大.这是由于装填不到位，弹丸在设计合膛位置之前就已经开始加速运动，因此弹丸的运动速度比装填到位时要大.2号单元在工况2下的等效应力明显大于其它工况，因为弹丸存在初始装填角，弹丸在加速的过程中，存在着一定的摆动，在弹带到达膛线起始处时，弹丸处于弹头向上倾斜的姿态，下方膛线起始处首先与弹带接触，因此受力较大，此时由于身管内膛下方与弹丸的作用，弹丸产生一个向下摆动的趋势.

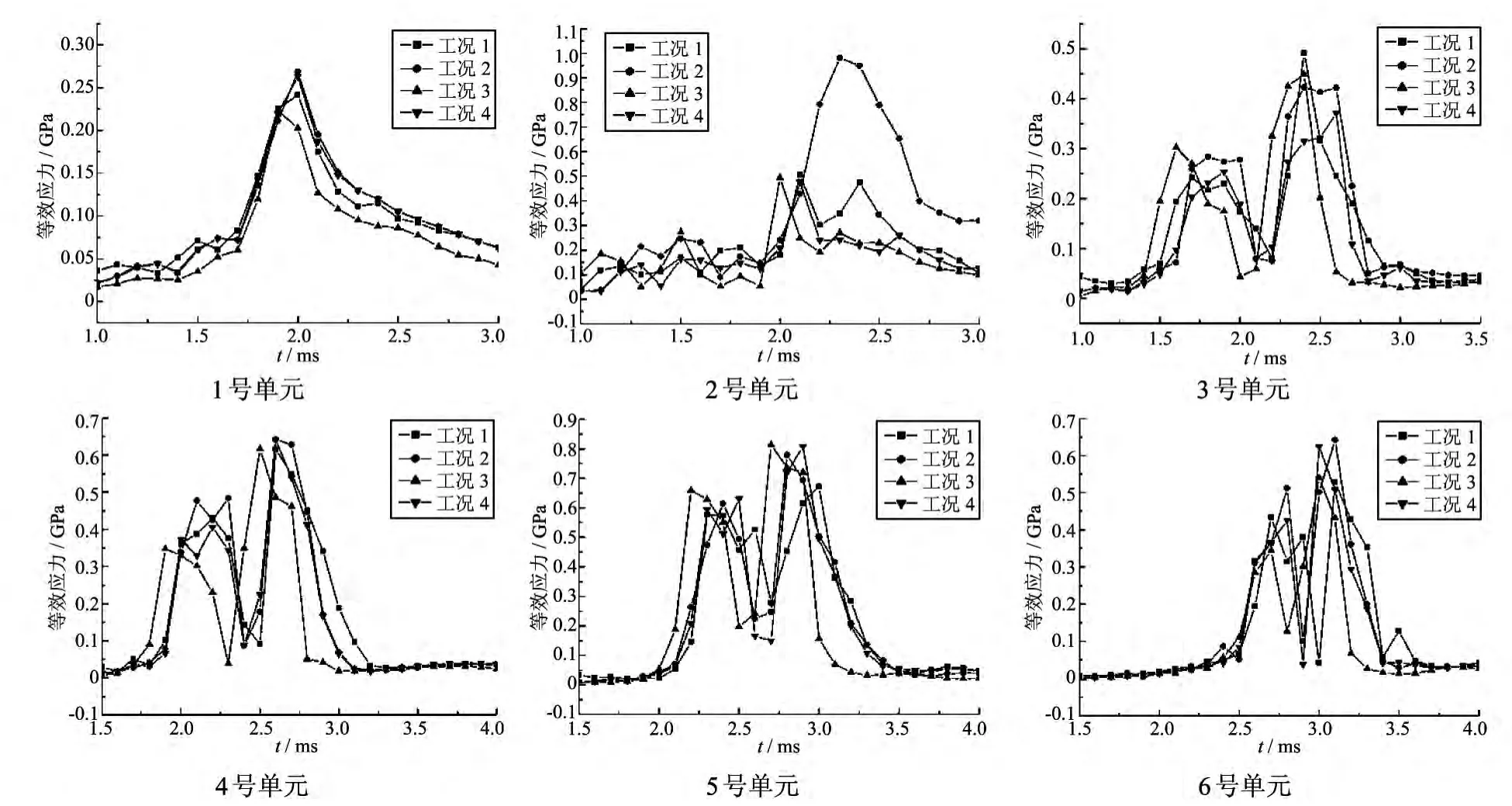
图9 各工况下阳线单元的等效应力Fig.9 Equivalent stress of elements of rifling rib in each operating mode

4.2 阳线损伤分析

图10 为大口径火炮实弹射击身管阳线损伤的形貌.由图中可以看出，损伤位置位于坡膛与直膛段过渡处附近，阳线双侧棱边呈大约45°八字形剥落，且阳线损伤断裂形状规整，断裂无明显韧性撕裂痕迹，但损伤阳线紧邻阳线有局部压缩塑性变宽的现象.

由身管应力分析可知，阳线损伤位置（5号单元附近）应力水平相对其它位置要高出许多，达到屈服极限附近，但这属于该火炮膛线结构及使用中的固有特征，同时考虑到身管材料的屈服极限随应变率的提高而增大，正常使用情况下不会造成阳线损伤.

图10 阳线损伤图Fig.10 Graph of rifling rib damage

下面对出现阳线损伤的机理进行分析.

身管材料为32CrNi3MoVE，其静态机械性能参数为：屈服极限1 184MPa，延伸率12%，断面收缩率25%，冲击韧性20J，静态强度与韧性达到了有效平衡.但对于炮钢材料，随着载荷作用速率的增加（应变率增加），其断裂韧性会随着下降，而屈服极限会有所提高.如炮钢PCrNi3MoV的静态断裂韧性为而动态断裂韧性只有（如表1 所示），屈服极限的变化如表2 所示.

表1 PCrNi3MoVA 材料的I，II型静、动态断裂韧性Tab.1 The I，II static and dynamic fracture toughness property of PCrNi3MoVA

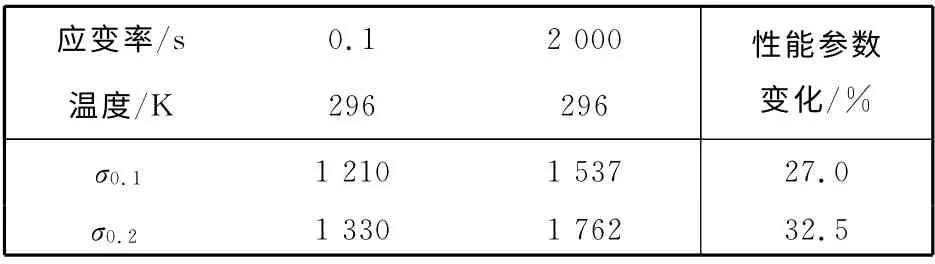
表2 PCrNi3MoVA 材料不同加载率（压缩）下的性能参数Tab.2 The performance parameters of PCrNi3MoVA under different loading rates

由于阳线在弹带挤进的过程中三面受非等值压缩，沿轴向受阳线长度方向约束，沿径向（从内向身管外表面）受身管壁厚约束，对阳线局部六面体单元而言，其本质为局部阳线单元受非等值六面压缩，如图11 所示（单元受剪应较小，对膛线损伤的贡献相对较小，可忽略不计）.

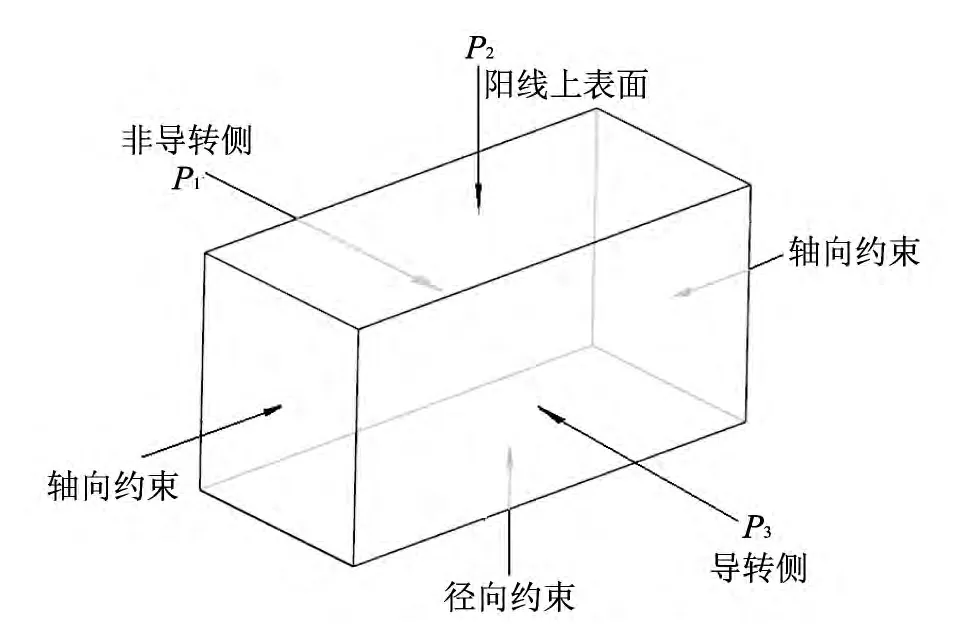
图11 阳线单元受力示意图Fig.11 Sketch map of stress of rifling rib

在弹带挤进的过程中，由于弹带与身管的过盈量从膛线起始至直膛段逐渐达到最大，因此弹带与阳线的相互作用不断增大.由于受到非等值六面压缩，阳线局部难以像受单向压缩（或拉伸）时的充分自由变形，不断增大的压缩力在阳线局部产生了过高的压缩应力，同时由于载荷作用速率的不断增大（如图12），使得阳线局部发生由韧性断裂到脆性断裂的转变，从而导致在实际阳线局部双侧棱边形成整齐的断裂形貌.

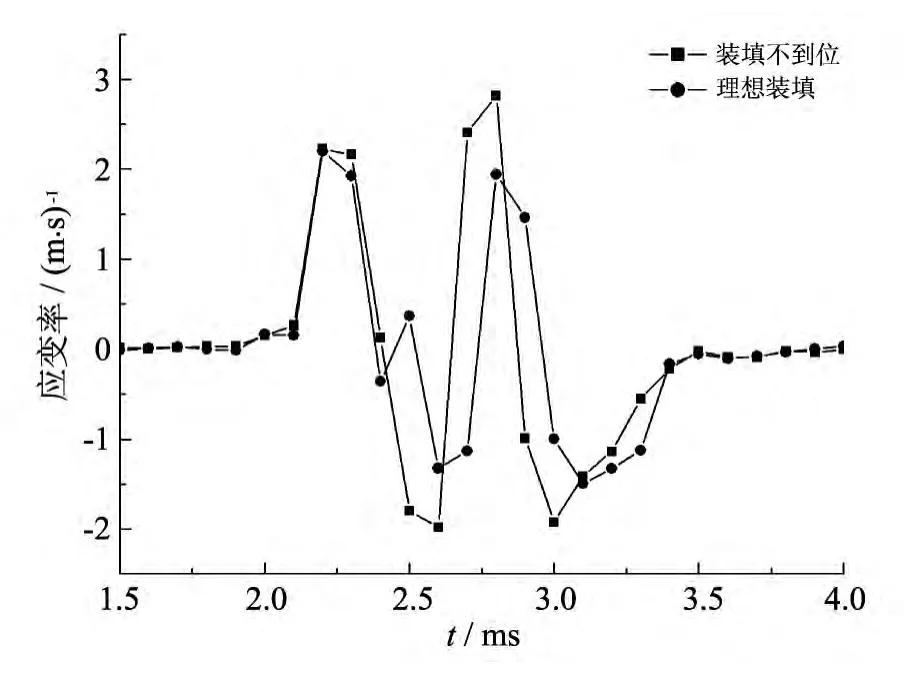
图12 不同装填情况下身管5号单元应变率对比Fig.12 Comparison of strain-rate of barrel 5under different filling conditions

由此可知，引起阳线损伤的原因，一方面是应力集中导致的局部应力水平增大，另一方面是加载速率增大导致炮钢材料断裂韧性降低而脆性增大.

弹带与身管径向过盈量是产生阳线压缩应力的主要因素，因此初始装填角、装填速度（合膛位置）等对阳线压应力影响不大.但由于弹丸初始装填角的存在，增加了膛线起始点到直膛开始段阳线动态应力的变化梯度，因而增加了出现阳线损伤的几率.

弹丸装填不到位时，弹丸在设计合膛位置之前就开始加速运动，弹丸运动速度比装填到位时大，致使身管加载速率提高，加剧了阳线局部发生由韧到脆断裂转变的可能性，因此考虑由于装填不到位导致的加载速率增大是出现阳线损伤的主要诱因之一.

5 结论

本文针对大口径火炮弹丸身管耦合系统，对弹丸挤进过程进行了数值分析.结果表明：坡膛和导向部过渡段应力集中严重，接近身管材料的屈服极限，与火炮实际使用过程中出现的膛线磨损和损伤问题相呼应；初始装填角和装填不到位对身管应力的大小影响不大，但初始装填角增加了身管应力变化的不确定性；弹炮间隙导致身管应力减小.研究结果为身管内膛结构与弹丸匹配设计，进一步进行弹丸挤进过程中的弹、炮动力的响应机理的研究奠定了基础.

针对大口径火炮使用过程中出现的阳线损伤现象进行了深入探讨，得出了弹丸装填不到位导致的加载速率增大是出现阳线损伤的主要诱因之一.研究初步揭示了阳线损伤的机理，即一方面是应力集中导致的局部应力水平增大，另一方面是加载速率增大导致炮钢材料断裂韧性降低而脆性增大.研究结论对损伤故障定位，缩小故障排查范围提供了重要的理论支撑.

［1］吴斌，郑靖.枪炮射击过程中弹丸与身管相互作用及其影响［J］.四川兵工学报，2011，32（5）：20-23.Wu Bin，Zheng Jing.Projectile interaction with gun barrel and its effect during firing process［J］.Journal of Sichuan Ordnance，2011，32（5）：20-23.（in Chinese）

［2］孙河洋，马吉胜，张高明，等.弹带挤进过程动力学仿真［J］.四川兵工学报，2008，29（5）：46-49.Sun Heyang，Ma Jisheng，Zhang Gaoming，et al.Dynamic emulation of engraving process on projectile［J］.Journal of Sichuan Ordnance，2008，29（5）：46-49.（in Chinese）

［3］彭涛，王学军，黄善文.基于ANSYS的弹带挤进变形及应力分析［J］.舰船电子工程，2009（11）：156-158.Peng Tao，Wang Xuejun，Huang Shanwen.Analysis on material deformation and stress in the process of driving band engraving based on ANSYS［J］.Ship Electronic Engineering，2009（11）：156-158.（in Chinese）

［4］韩文祥.弹丸挤进变形模拟问题研究［D］.南京：南京理工大学，2009.

［5］孙河洋，马吉胜，李伟，等.坡膛结构变化对弹带挤进过程影响的研究［J］.振动与冲击，2011，30（3）：30-33.Sun Heyang，Ma Jisheng，Li Wei，et al.Influence of different bore structures on engraving process on projectile［J］.Journal of Vibration and Shock，2011，30（3）：30-33.（in Chinese）

［6］樊黎霞，何湘王月.弹丸挤进过程的有限元模拟与分析［J］.兵工学报，2011，32（8）：963-969.Fan Lixia，He Xiangyue.Finite element simulation and process analysis of prpjectile entering into barrel［J］.Acta Armamentarii，2011，32（8）：963-969.（in Chinese）

［7］冷冰林，许金余，邵宁，等.刚性弹丸侵彻金属靶体的FEM-SPH 耦合计算［J］.弹箭与制导学报，2008，28（5）：105-108.Leng Binglin，Xu Jinyu，Shao Ning，et al.Computation of steel penetrated by rigid projectile with coupled FEM-SPH methods［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2008，28（5）：105-108.（in Chinese）

［8］龚洁.汽车前保险杠碰撞的有限元仿真分析研究［D］.沈阳：东北大学，2010.

［9］张雄，王天舒.计算动力学［M］.北京：清华大学出版社，2007.