倾倒式岩质崩塌运动过程数值模拟分析

袁志辉，陈志新，倪万魁，张文栋，王 博

(长安大学地质工程与测绘学院，陕西西安 710054)

0 引言

崩塌一般是指陡峭边坡所发生的一种突然而又急剧的动力地质现象，即在地势陡峭、地质条件复杂的边坡上，其上的岩体或土体在自重和其它外力作用下，突然脱离母岩而急剧向下崩落［1］。崩塌是一种突发性的地质灾害，虽然规模不大，但破坏性强，常给人民的生命财产造成重大的损失。崩塌的孕发过程具有渐进性、失稳过程具有突发性［2］。崩塌的破坏模式和运动形式目前尚未有统一的分类，从不同的角度出发存在不同的分类，陈明东根据受力模式将崩塌失稳破坏分为板梁旋滑移和悬臂压杆破坏两类［3］;张奇华将崩塌失稳模式分为八类，即蠕滑体滑移失稳、整体压陷倾斜崩塌、滑移—倾斜交错崩塌、裂隙段屈曲变形破坏、上下滑出破坏、倾斜—滑移破坏、倾斜—隐裂缝开裂—崩塌、倾斜—滑移—隐裂缝开裂—崩塌［4］;孙志云将崩塌失稳模式分为滑移和倾倒两类。曾廉将崩塌落石的运动形式分为坠落、跳跃、滚动和滑动，多数情况下为跳跃和滚跳的组合［1］;赵旭根据运动学原理将崩塌落石分为坠落、滑动、滚动和弹跳等阶段［5］;唐红梅将崩塌下落分为四个阶段，即初始位移阶段，碰撞阶段，滑动阶段和滚动阶段［6］。

虽然目前对崩塌的研究越来越深入，但对崩塌的破坏、运动过程和运动轨迹的研究还不够深入。由于该问题十分复杂，用理论方法难以描述其实际运动过程，因此本文运用2D-Block离散元软件对延长县典型倾倒式崩塌进行破坏和运动过程的数值模拟，分析其破坏过程和运动规律，并通过理论计算公式和数值模拟的对比，得出了崩塌的崩滑距。

1 离散元程序原理

离散单元法是20世纪70年代兴起的一种数值计算方法，主要是求解众多具有节理和裂隙岩体在外力作用下的相互作用以及运动过程的有效方法。2DBlock离散程序基于块体准刚性假设，以牛顿第二定律为理论基础研究块体的运动特征，并模拟地质体的宏观大变形。其基本思想是将岩土体视为由节理、裂隙和层理切割的非连续介质，构成块体的集合体，当集合体的作用力或其边界约束发生变化时，块体间会产生应力的重分布，并导致块体产生一定的加速度和相应的位移，使其空间上发生很大的变化。位移的块体之间，由于差异位移矢量的存在，块体之间彼此又发生新的作用，根据力—位移关系，按“叠合”位移重新计算新的作用力系，从而计算出集合体各块体在新力系下加速度、位移和新的运动位置，如此反复迭代，直至整个体系作用的力系最终达到平衡，岩土体的运动过程也就被真实的模拟出来。

尽管该离散元程序专门用于节理岩体大变形的分析，但存在一定的局限性，即节理的裂隙应是相互贯通的，而岩体节理的实际连通率是有限的，鉴于本文主要研究的是崩塌的运动过程，因此只考虑岩体中已贯穿或基本贯通的节理裂隙，而对于岩体内部未贯穿的节理裂隙不做考虑。

2 崩塌的运动过程分析

2.1 倾倒式崩塌概况

选取延长县甘谷驿崩塌进行实例分析。该崩塌属小型岩质崩塌，位于延长县与延安市交界处的延延公路旁，为修建公路形成的岩质人工破碎高陡边坡。坡体长5m，坡高18.8m，坡宽为100m，边坡坡度近乎直立，坡向285°，坡面凹凸不平，局部区域形成鹰嘴岩。基岩为三叠系中统铜川组砂岩夹泥质页岩，岩体产状为310°∠4°。上部砂岩比较厚，厚度最大为5.2m，中下部砂岩厚度约为2m，泥质页岩厚度一般为0.1～0.5m。坡面岩体比较破碎，节理裂隙较发育，将岩体切割成不规则块体，主要发育有三组节理裂隙，分别为 320°∠80°、305°∠90°、5°∠77°。

虽然斜坡岩体近水平状产出，但由于修建公路的开挖爆破和薄层泥质页岩的风化剥蚀，下部砂岩和页岩被掏空，使得上部巨厚层砂岩悬空，且坡体后缘见一条长约10m，缝宽约0.2～0.8m，深约5m的裂缝，在重力和水压力的作用下发生倾斜，并最后形成崩塌;根据坡脚崩塌堆积物在公路产生的陷坑和访问村民，推测该崩塌落石运动的最远距离为8.3m。

2.2 模型建立和边界条件

地质模型采用实测工程地质剖面，模型宽18m，高18.8m，选定层面、各节理面作为结构面来划分单元(图1)，将模型的左边界、下边界和公路作为固定边界，对其进行约束，整个计算过程中不发生横向和竖向位移;其他边界为自由边界。

图1 甘古驿崩塌地质模型Fig.1 Geological model of collapse in Ganguyi

2.3 参数选取

表1 数值模拟采用的力学参数Table 1 Mechanical parameters in numerical simulation

2.4 模拟结果分析

模拟结果如图(图2～5)所示，形象地再现了倾倒式崩塌的破坏和运动过程。斜坡岩体经历了岩体节理开裂变形、岩体沿基座支点的倾倒运动、崩塌体在一定初速度下的落体运动、崩塌体的碰撞与堆积四个阶段。

2.4.1 岩体原有节理开裂变形阶段

图2可以看出，斜坡的上部大块岩体在重力和其他作用下(地震和孔隙水压力等)出现了拉张裂隙，并逐渐扩大;下部小块岩体在裂隙存在的条件下由于重力的作用发生坠落运动;斜坡上部的黄土体由于幔覆于砂岩之上，大块砂岩的拉张裂隙使得上部黄土体产生了应力的重分布，并出现了一系列的拉张裂隙。

图2 岩体节理裂隙开裂变形Fig.2 Cracking and deformation of rock mass joints

2.4.2 岩体沿基座支点的倾倒运动阶段

图3可以看出，随着裂隙的逐渐扩大，上部大块岩体开始逐渐脱离母岩，并在重力的作用下沿基座支点发生倒转运动;上部部分黄土体由于节理的存在，在重力作用下也开始出现了裂隙，并有下坠的趋势;而下部小块砂岩在重力的作用下已经完成了整个崩塌运动的全过程，经过与地面的碰撞，在地面形成了堆积。

图3 岩体沿基座支点的倾倒运动Fig.3 Toppling of rock mass along the fulcrum of base

2.4.3 崩塌体在一定初速度下的落体运动阶段

图4可以看出，上部大块砂岩已经脱离母岩，沿基座支点的倒转运动已经完成，在倾倒作用产生的初速度下以重力加速度做落体运动，大块岩体的运动距离取决于倾倒运动完成时具有的初速度和斜坡的高度;上部部分黄土体的裂隙进一步扩大，并在重力的作用下逐渐开始解体和下坠。

图4 崩塌体在初速度下的落体运动Fig.4 Falling of collapse bodies in certain initial velocity

2.4.4 崩塌体的碰撞与堆积

图5可以看出，上部大块砂岩和部分黄土体在重力的作用下已经完成了整个崩塌的全过程，在下坠过程中与地面碰撞弹跳后停止运动形成堆积。由于公路是平整的，所以崩塌体经过与公路的碰撞后并不会发生较大的水平位移，因此不会出现翻滚运动。同时可以很明显的看出，上部部分黄土体虽然产生比较大的拉张裂隙却没有下坠，如果在外界条件(雨水冲刷、振动等)作用下有进一步下坠的趋势，并在坡脚堆积。

图5 崩塌体的碰撞与堆积Fig.5 Collision and accumulation of collapse bodies

通过模拟结果显示，倾倒式崩塌经历了较典型的四个阶段，特点为岩块体积比较大，脱离母体突然，速度快，冲击力大，致灾范围比较远。

3 影响范围分析

对于崩塌影响范围的研究一般采用两种方法来进行确定:(1)崩塌历史调查，从斜坡崩落物质分布，历史上落石事件的调查和反演，推断崩塌的运动距离和范围;(2)利用Spang R M依据功能原理，崩塌的势能变化等于动能和克服摩擦所做的功的理论计算得出的崩塌的距离。但很多时候斜坡只是处于临界变形阶段，并没有发生崩塌，因此方法(1)存在一定的局限性;同时依据功能原理也存在一定的缺陷，在崩塌的运动过程中岩块之间的碰撞是其无法考虑进去的一个重要因素，因此很多时候只能依据数值模拟和理论计算两者结合来确定崩塌的影响范围。

3.1 倾倒式崩塌初始速度公式

唐红梅和叶四桥等人根据动力学和动能定理提出了初始运动速度公式［7］为:

式中:

g——重力加速度(m/s2);

b——块体对角线长度(m);

γ——岩块对角线转动角度(°);

v0——危岩倾覆运动末时刻初始速度(m/s)，其与水平方向夹角为γ-e，e为原始位置危岩块体对角线与竖直方向的夹角(°)。

唐红梅和叶四桥等人的文中认为危岩倾覆运动末时初始速度与水平方向的夹角γ-e，但笔者通过分析认为危岩体倾覆运动末时的初始速度v0与水平方向的夹角分为两种情况，一种是当支点O与块体质心C的连线位于第四象限时，危岩体倾覆运动末的初始速度与水平方向夹角为γ-e;另一种是当支点O与块体质心C的连线位于第一象限时，危岩体倾覆运动末时初始速度与水平方向夹角为γ+e，具体见图6、图7。

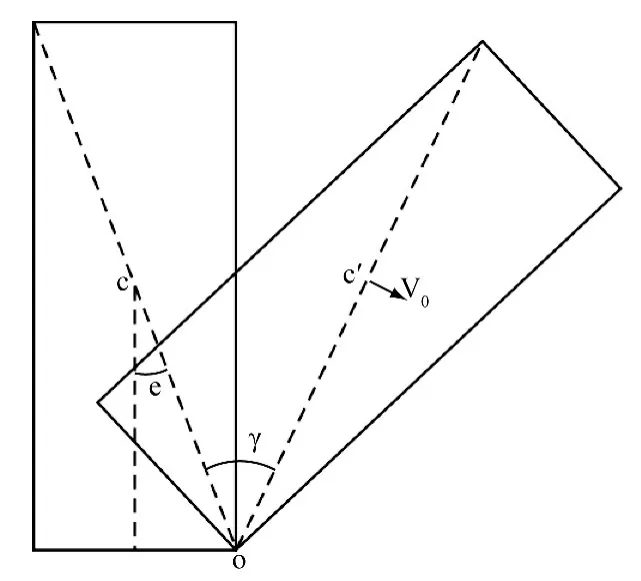
图6 倾倒式破坏初始运动状态图Fig.6 Initial motion map of toppling Collapses

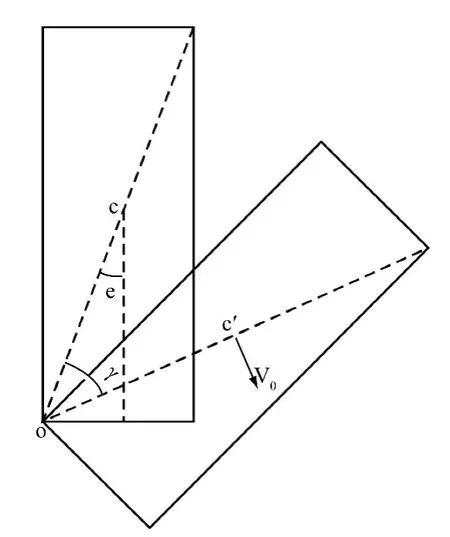
图7 倾倒式破坏初始运动状态图Fig.7 Initial motion map of toppling Collapses

当为第一种情况时，其危岩体倾覆运动末时的初始速度是分解为水平方向和竖直方向为:

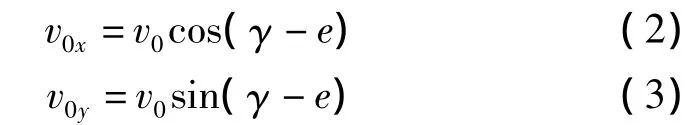
当为第二种情况时，其危岩体倾覆运动末时的初始速度是分解为水平方向和竖直方向为:

3.2 崩塌影响范围理论计算和数值模拟结果

根据图8，对于b的取值可以将岩块近似看成规则块体，其值约为5.3m;γ的值为岩块对角线转动角度，因岩块为刚体，所以γ的值也可看成是岩块上任何一条过支点O的直线经过转动后的角度，该文以OC(C点为岩块质心)和OC'之间的角度为γ，其值为40°;e的取值为15°。根据公式(1)可以得出:v0=4.50m/s，根据公式(4)和(5)将v0分解为x和y方向的速度得:v0x=2.58m/s，v0y=3.68m/s。

图8 甘谷驿崩塌初始速度示意图Fig.8 Initial velocity map of collapse in Ganguyi

根据大块岩体在初速度v0下的自由落体运动公式:

其中H为大块岩体初始位置时质心与堆积后质心之间的垂直距离，此处H=12m，通过公式(6)可以得出大块岩块的下落时间为t=1.24s。

根据公式:

式中:S为岩块运动开始和结束后其质心之间的水平距离。

通过公式(7)可以得出大块岩块的运动距离为S=3.20m

根据图9得出，假设大块岩体是规则块体，那么其运动距离为S，其值的模拟结果为S=3.32m，但由于大块岩体的不规则，其在与平坦地面碰撞后发生了一个倒转运动，所以大块岩体实际质心之间的距离为S'=4.68m;而受大块岩体的大小和形状的影响，数值模拟下崩塌的影响范围为S″=7.72m。

图9 大块岩体的运动距离(模拟结果)Fig.9 Movement distance of bulk rock(simulation results)

3.3 实际调查与理论计算和数值模拟结果对比

理论计算所得到的崩塌的运动距离为3.20m，在计算中将大块岩体近似看成规则，其对角线之间距离b的取值为5.3m，因此理论计算所得出的最终影响范围为5.85m;数值模拟得出的崩塌影响范围为7.72m，而实际调查得出的该崩塌影响范围为8.30m。

从三者之间的数值关系来看，理论计算远小于数值模拟和实际调查结果，其原因主要是理论计算将大块岩体看成是规则的，而实际情况并非如此，同时理论计算难以考虑崩塌体在坠落过程中与斜坡上的基岩和已坠落堆积的岩体之间的碰撞，以及不规则岩体在堆积过程的平衡;而数值模拟结果稍小于实际调查结果，笔者认为数值模拟时力学参数是在试验和经验基础上得到的，虽然在量级上与岩体力学参数一致，但不可能等于真值;其次崩塌大部分是在降雨作用下发生的，雨水渗入裂隙中，除了增加水压力之外，应该还对岩体之间的咬合起到了润滑的作用，节理摩察角变小，但本文未考虑此影响;因此数值模拟结果稍小于实际调查结果，但两者基本一致。

4 结论

通过对倾倒式崩塌的数值模拟，有效的论证和补充解释该类崩塌的变形、破坏过程，能够较好的模拟崩塌的运动全过程，当然数值模拟也存在一定问题，尤其是地质模型精确性有待于进一步加强。

(1)通过对倾倒式崩塌的数值模拟，形象的再现了这类崩塌的破坏和运动过程。

(2)倾倒式崩塌破坏和运动过程分为岩体原有节理开裂变形、岩体沿基座支点的倾倒运动、崩塌体在一定初速度下的落体运动、崩塌体的碰撞与堆积四个阶段。

(3)数值模拟所得倾倒式崩塌的大块岩体的实际影响范围要大于理论计算，与实际调查结果相接近，因此数值模拟方法得到的结果可作为倾倒式崩塌的影响范围预测，且弥补了理论计算中无法考虑岩块之间相互碰撞的因素。

［1］曾廉.崩塌与防治［M］.成都:西南交通大学出版社，1990 ZENG Lian.Rock Fall and Control［M］.Chengdu:SouthwestJiaotong University Press，1990.

［2］陈洪凯，王蓉，唐红梅.危岩研究现状及趋势综述［J］.重庆交通学院学报，2003，22(3):80-88 CHEN Hongkai，WANG Rong，TANG Hongmei.Review on current situation to study and trend of dangerous rock mass［J］.Journal of Chongqing Jiaotong University，2003，22(3):80-88.

［3］陈明东.链子崖危岩体变形破坏机制及整治对策［J］.地质灾害与环境保护，1999，2(1):33-42 CHEN Mingdong.Deformation-failure mechanism and treatment measures of Lian zi cliff［J］.Journal of GeologicalHazards and Environment Preservation，1999，2(1):33-42.

［4］张奇华，彭光忠，付少兰，等.链子崖危岩体变形破坏系统辨识［J］.岩石力学与工程学报，1998，17(5):544-551.ZHANG Qihua，PENG Guangzhong，FU Shaolan，et al.System dentification of deformation-failure for the dangerous rock body of Lian zi cliff［J］.Chinese Journal of Rock Mechanics and Engineering，1998，17(5):544-551.

［5］孙志云，任自民，王立，等.奉节李子垭危岩体稳定性研究［J］.人民长江，994，25(9):48-53.SUN Zhiyun，REN Zimin，WANG Li，et al.Stability analysis of dangerous rock body of Li Ziya，in Feng Jie City，Journal of Yangtze River，1994，25(9):48-53.

［6］唐红梅，易朋莹.危岩落石运动路径研究［J］.重庆建筑大学学报，2003，25(1):16-21.TANG Hongmei，YI Pengying.Research on dangerous rock movement route［J］.Journal of Chongqing Jiaozhu Uiversity，2003，25(1):16-21.

［7］叶四桥，唐红梅，祝辉.基于落石运动特征分析的拦石网设计理念［J］.岩土工程学报，2007，29(4):566-571.YE Siqiao，TANG Hongmei，ZHU Hui.Dsign conception of safe net system based on analysis of motion trace of rockfall［J］.Chinese Journal of Geotechnical Engineering，2007，29(4):566-571.

［8］胡厚田.崩塌落石研究［J］.铁道工程学报，2005(s):387-392.HU Houtian.Research on the collapse and falling stone［J］.Journal of Railway Enginnerging Society，2005(s):387-392.

［9］王念琴，张倬元.黄土滑坡灾害研究［M］.兰州:兰州大学出版社，2004.WANG Nianqin，ZHANG Zhuoyuan.Study on loess landslide disaster［M］.Lanzhou:Lan Zhou Uiversity Press，2004.

［10］赵晓颜，胡厚田，等.万县长江三峡库区塌岸的数值模拟分析［J］.水土保持学报，2003，17(5):158-160.ZHAO Xiaoyan，HU Houtian，et al.Numerical simulation of rochfall of Wanxian Yangtze river reservior bank［J］.Journal of Soil and Water Conservation，2003，17(5):158-160.

［11］Bozzolo D，Pamini R.Simulation of rockfalls down a valleyside［J］.Acta Mcch，1986，63:113-130.

［12］Dayr W.Case studies of rockfall in soft versus hard rock［J］.Environmental and Engineering Geoscience，1997 ，3(1):133-140.

［13］吴谨，黄仁熊，邹启学，等.贵州开阳磷矿区崩塌及其防治［J］.中国地质灾害与防治学报，2011，22(3):27-32.WU Jin，HUANG Renxiong，ZOU Qixue，et al.Rock falls and their prevention in phosphorus area of Kaiyang county，Guizhou province［J］.Chinese Journalof Geological Hazard and Control，2011，22(3):27-32.

［14］丁坚平，李扬，诸学伟，等.贵州开阳县龙井湾崩塌地质灾害评估与防治［J］.中国地质灾害与防治学报，2006，17(4):21-24.DING Jianping，LI yang，ZHU Xuewei，et al.Evaluation and prevention of rock fall Longjianwan，Guizhou province［J］.The Chinese Journal of Geological Hazard and Control，2006，17(4):21-24.