水－异丁醇二元体系溶解度和液液相平衡

金春英，林金清

（1.华侨大学 化工学院，福建 厦门361021；2.华侨大学 材料科学与工程学院，福建 厦门361021）

异丁醇与水是羰基合成法生产高级醇类的主要副产物，在用精馏法分离这些醇类粗产品时，需要各种醇－醇、醇－水体系的相平衡数据.异丁醇－水体系是极性缔合溶液，在一定温度和组成范围内，两组分呈现部分互溶状态，而在此范围之外，又可以形成两相.由于两个相内的极性不同，可以分别溶解不同极性的物质，因此可以用该体系来分离提纯不同极性的有机物，如用异丁醇从含酚废水中萃取出苯酚［1］，用异丁醇从发酵液中提取沸点较高的2，3－丁二醇［2］等.文献［3］报道了水－异丁醇二元体系的液液相平衡数据，并用非随机（局部）双液体（NRTL）模型进行关联，但关联后异丁醇在水相和醇相中的平均绝对误差分别为0.059 8（水相）和0.069 7（醇相），平均相对误差分别为349.3%（水相）和17.31%（醇相），误差较大.本文采用浊点法测定了水－异丁醇二元体系在常压、温度范围为25～60℃的溶解度和液液相平衡数据，用NRTL方程进行关联计算，并重点考察温度对模型参数的影响，以及引用文献报道的，从二元汽液相平衡数据关联得到的模型参数直接预测液液相平衡关系的可能性.

1 实验部分

1.1 试剂与仪器

试剂：异丁醇，分析纯，纯度≥99.7%，上海化学试剂公司；蒸馏水（自制）.仪器：自制平衡釜，带循环水夹套，由超级恒温浴提供恒温水（其控温精度为±0.1K），配有强力电磁搅拌器.

1.2 试验方法

对于二元部分互溶的液体溶液，当两个液相达到平衡时，体系的自由度为2，因此，在常压下二元体系的相平衡关系只是温度的函数.实验采用浊点法［4］，在自制的平衡釜中测定溶解度数据.即在一定温度，一定量的水中缓慢加入异丁醇（或是一定量的异丁醇中缓慢加入水），磁力搅拌至溶液刚出现混浊，此时的溶解度即为该温度下异丁醇在水（或水在异丁醇）中的饱和溶解度，由此测定的一组饱和溶解度数据即为该温度下的二元体系的液液相平衡数据.

1.3 试验结果

实验测得溶解度数据和液液相平衡关系，如表1所示.表1中：t为 温 度；x1，1，x1，2分别表示上、下相中水的摩尔分数.

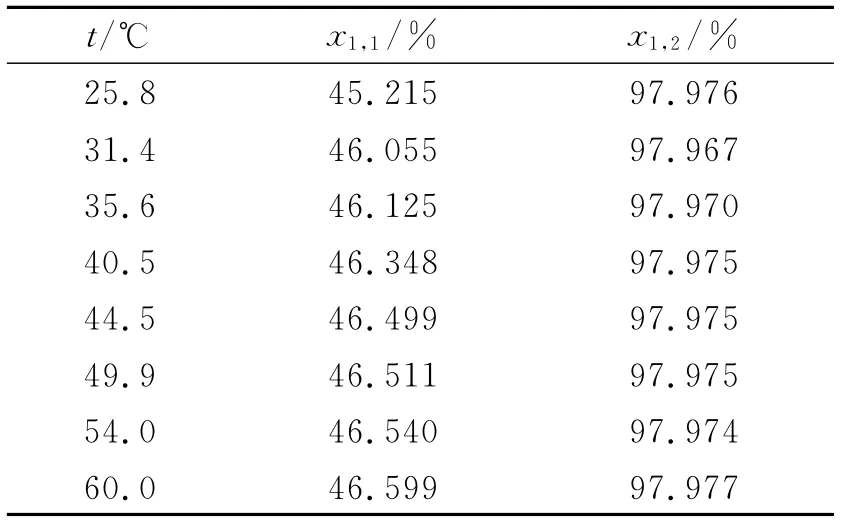
表1 水－异丁醇二元溶解度和液液相平衡数据Tab.1 Solubility and liquid－liquid equilibrium on the binary system of water－isobutanol

2 计算方法与结果分析

2.1 相平衡方程及计算方法

液液相相平衡方程为

经归一化后可得

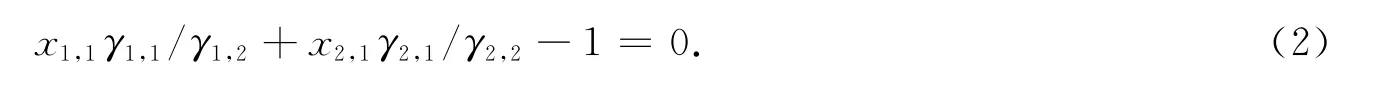
式（2）中：γ1，1＝f（x1，1，x2，1）；γ1，2＝f（x1，2，x2，2）；γ2，1＝f（x1，1，x2，1）；γ2，2＝f（x1，2，x2，2）.γi，j可用NRTL方程计算，其中，下标i为组分，j为相.

在一定温度下，x1，1已知，则x2，1＝1－x1，1，因x2，2＝1－x1，2，故式（2）是一个关于x1，2的超越方程.因此，已知任一组分的组成求平衡时，其余组分的组成是一个求解超越方程的问题，可用数值法［5］求解，本文采用ZEROIN算法.

2.2 溶液热力学模型和参数预测

2.2.1 NRTL方程 对于水－异丁醇体系上、下相中，水（1）和异丁醇（2）的活度系数模型可采用NRTL方程.对于二元体系，NRTL方程给出的计算公式为

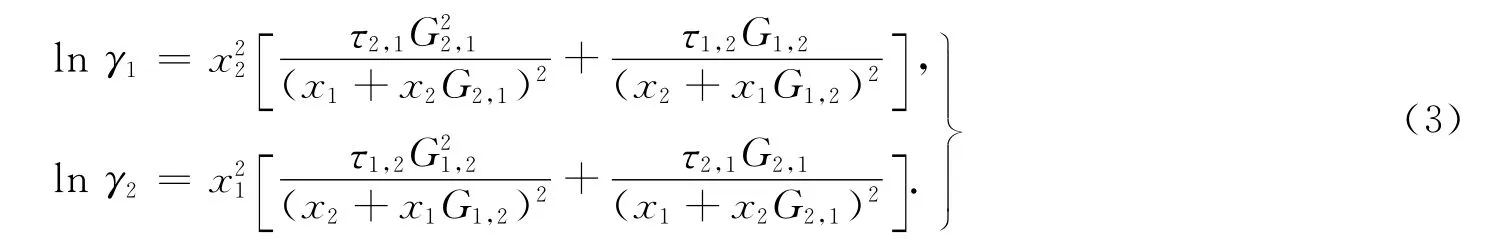
2.2.2 模型参数的回归 由式（3）可知，二元体系NRTL方程的模型参数有α1，2，G1，2和G2，1.这些参数可以由实验数据回归得到.根据参数α1，2，G1，2和G2，1是否是温度的线性函数，设置了如下5种不同处理方式：

1）α1，2，G1，2和G2，1均为常数；

2）α1，2＝a1＋b1t，而G1，2，G2，1为常数；

3）α1，2＝a2＋b2t＋c2t2，而G1，2，G2，1为常数；

4）G1，2＝a3＋b3t，G2，1＝a4＋b4t，而α1，2为常数；

5）G1，2＝a5＋b5t，G2，1＝a6＋b6t，α1，2＝a7＋b7t.

文中采用基本遗传算法［6－9］，并用FORTRAN 90编程，分别得出5种不同处理方式的目标函数，如表2所示.从表2的目标函数值看，5种不同处理方式中，第5种方式的目标函数值最小，即在G1，2，G2，1，α1，2均作为温度的一次函数情况下，实验值与计算值最为接近.

表2 不同处理方式的目标函数值Tab.2 Comparison of objective function values

由回归计算得到的水－异丁醇模型参数，如表3所示.表3中同时列出了文献［10］从二元汽液相平衡数据关联得到的该二元体系的模型参数值.

2.2.3 相平衡计算结果 用FORTRAN语言编程计算，结果如表4所示.表4中：x1，ref为文献［3］报道的上相中组分1（水）含量的值；x1，exp为实验值；xi，cal，i＝1，2，…，5为表2中5种处理方式各参数条件下的NRTL模型计算值；xcal为从文献［10］二元汽液平衡参数的预测计算得到的NRTL模型计算值.

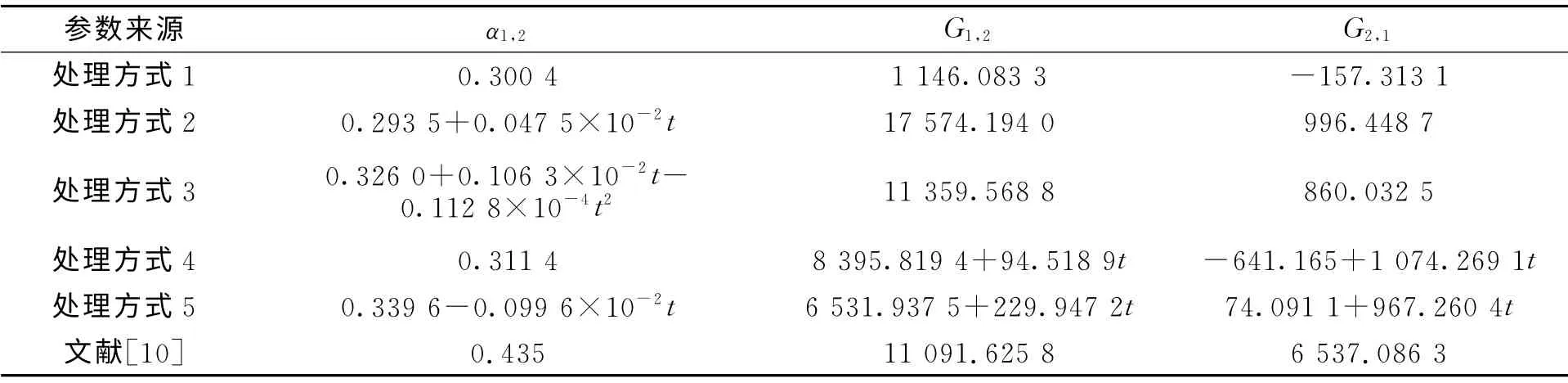
表3 水－异丁醇的NRTL方程参数表Tab.3 NRTL equation parameters table of water－isobutyl alcohol

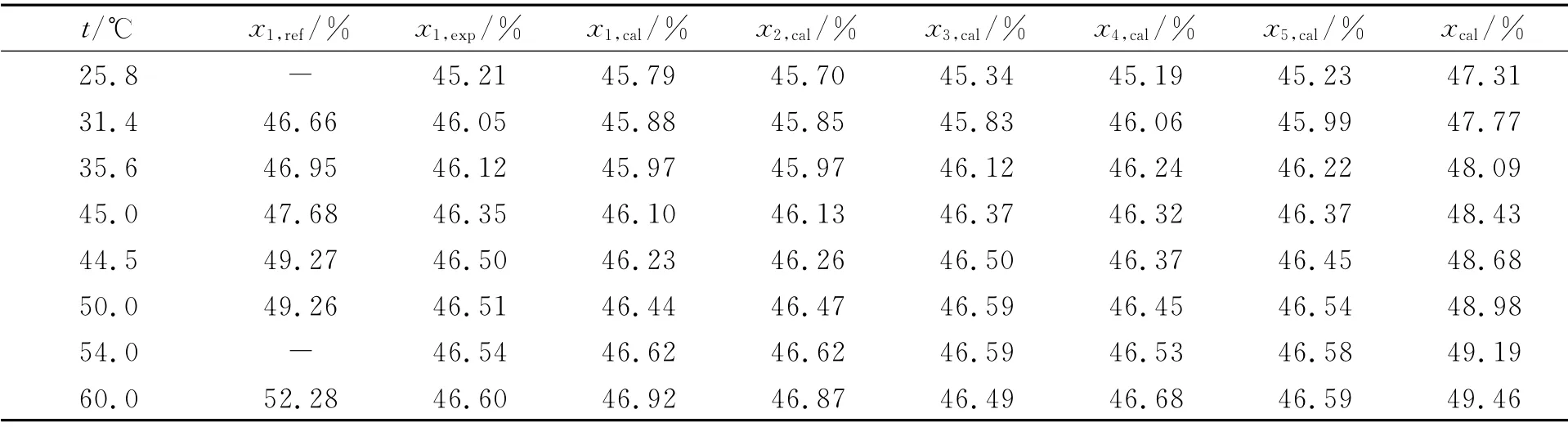
表4 水－异丁醇液液相平衡计算结果Tab.4 Calculated results of water－isobutyl alcohol liquid－liquid equilibrium

参数α1，2，G1，2和G2，1经计算得到平均绝对误差和相对误差，如表5所示.表5中：Δav表示平均绝对误差，；δav表示平均相对误差；δmax表示最大相对误差.

表5 计算结果的误差比较Tab.5 Error comparison of the calculated results

因此，由以上结果可知，采用文献参数代入NRTL方程的平均相对误差为4.87%，最大相对误差为6.14%，且均为正偏差，计算结果并不是很理想.说明用从二元的汽液相平衡数据关联得到的模型参数，直接来预测二元的液液相平衡关系仍可能存在较大的偏差.究其原因，可能是由于在沸点附近汽液两相间的相互作用力与在30～60℃时液液两相间的相互作用力有较明显的差异引起的.

由遗传算法将从实验测得的二元液液平衡数据进行回归，并将所得到的参数代回NRTL方程，其计算结果与实验值均很接近，特别是用遗传算法计算的处理方式5，其计算值与实测值的相对偏差最小，平均绝对误差仅为0.000 4，平均相对误差只有0.09%，说明温度对本二元体系的模型参数有一定的影响.当考虑二者之间为线性关系时，其关联精度最高，但取与温度无关的常数，其最大相对误差为0.69%，平均相对误差为0.51%，已能满足关联精度要求.这可能是由于文中所研究的温度范围较小，所以参数对温度的依赖性还不明显.

3 结束语

文中采用浊点法测定了水－异丁醇二元体系的溶解度及液液相平衡数据，并用遗传算法对该体系NRTL方程的二元相互作用参数进行了回归计算.同时，将文献参数值和遗传算法回归计算得到的参数值分别代入NRTL方程，考察了预测和关联精度.结果表明：用从二元的汽液相平衡数据关联得到的模型参数直接来预测二元的液液相平衡关系仍可能存在较大的偏差；而用遗传算法回归得到的参数代回计算，可得到满意的关联精度.此外，温度对本二元体系的模型参数有一定的影响.研究异丁醇－水的液液相平衡关系，可为水溶液中不同极性物质的分离提取提供了一种思路和基础数据.

［1］居红芳，徐桦，朱慧，等.水－异丙醚－苯酚和水－异丁醇－苯酚体系的液液平衡研究［J］.高校化学工程学报，2009，23（1）：12－17.

［2］WU Yan－yang，PAN De－tao，ZHU Jia－wen，et al.Liquid－liquid equilibria of water＋2，3－butanediol＋isobutanol at several temperatures［J］.Fluid Phase Equilibria，2012，325（15）：100－104.

［3］童安渝，苏裕光.异丁醇－水体系液液平衡研究［J］.成都科技大学学报，1986（2）：13－17.

［4］谭平华，林金清，陈培钦，等.异丙醇－磷酸氢二钾－水三元体系的溶解度和液液相平衡［J］.华侨大学学报：自然科学版，2003，24（2）：179－183.

［5］宋岱才，路永洁，刘国志，等.数值计算方法［M］.北京：中国经济出版社，2006：114－125.

［6］RANGAIAH G P.Evaluation of genetic algorithms and simulated annealingfor phase equilibrium and stability problems［J］.Fluid Phase Equilibria，2001，187－188（15）：83－109.

［7］贾冬梅，邓文生.用混合遗传算法求解相平衡和化学平衡［J］.计算机与应用化学，2011，28（9）：1175－1178.

［8］林金清，李浩然，韩世钧.应用遗传算法求解含化学反应体系的相平衡［J］.化工学报，2002，53（6）：616－620.

［9］安维中，胡仰栋，袁希钢.多相多组分化学反应平衡和相平衡计算的遗传算法［J］.化工学报，2003，54（5）：692－694.

［10］周金汉，钱栋英，蒋淇忠.发酵酒精中微量杂质的三元减压汽液平衡数据的测定和关联［J］.化工学报，1994，45（6）：764－766.