产生尺寸可调局域空心光束的技术

何西，吴逢铁，李冬，李攀

（华侨大学 信息科学与工程学院，福建 厦门361021）

1987年，J.Durin等［1］提出了无衍射光束的概念，其后光束的无衍射和自重建特性引起了人们极大的兴趣，而由其变换后得到的局域空心光束（bottle beam）［2］也在各个领域得到了广泛的应用.所谓局域空心光束就是光束沿光传播方向上，有着强度为零的区域，而在此区域外三维空间都围绕着高强度的光［3］.由于局域空心光束具有三维封闭的暗中空区域和极高的强度梯度，可作为激光导管［4］、光镊［5］和光学扳手［6－7］等有力工具，还可用于激光囚禁和操控不同种类的微观粒子［8］，包括纳米量级或微米量级的粒子，甚至原子团簇和生物粒子或活细胞等.因此，获得尺寸可调局域空心光束的技术对于捕获和操控不同尺度的微粒是非常必要的.目前，获得尺寸可调局域空心光束的方法有多种，文献［9－11］对此做了较深入的研究.本文对轴棱锥透镜系统、新型组合正轴棱锥、液体轴棱锥、可拆式组合轴棱锥，以及聚焦多环空心高斯光束产生尺寸可调局域空心光束的方法进行总结与比较.

1 轴棱锥透镜系统产生尺寸可调的局域空心光束

图1 轴棱锥透镜系统产生bottle beam轴向三维光强分布图Fig.1 3－D distribution of intensity on axis generated by axicon－lens system

S.Chavez－Cerda等［12］提出利用轴棱锥透镜系统产生贝塞尔光束并聚焦形成局域空心光束.在局域空心光束中，光束沿光传播方向上有着强度为零的区域，而在此区域外三维空间都围绕着高强度的光，如图1所示.

Ming－Dar Wei等［13］研究了轴棱锥透镜系统中产生局域空心光束的条件及其形成过程，但并未对局域空心光束尺寸变化做进一步研究.文献［14－21］从几何光学，波动光学等方面对局域空心光束及其尺寸变化做了较深入的研究，其中文献［14］研究了轴棱锥－透镜系统中透镜与轴棱锥距离，光阑半径及透镜焦距对于局域空心光束尺寸变化的影响.轴棱锥透镜系统产生局域空心光束的实验装置和原理，如图2所示.

局域空心光束的横向暗斑尺寸与焦距成正比，纵向暗斑尺寸与聚焦透镜到轴棱锥间的距离z0及光阑半径成反比，而与焦距成正比，因此，改变聚焦透镜的焦距和聚焦透镜到轴棱锥间的距离及光阑半径，可有效地改变局域空心光束的大小，从而可获得尺寸可调的局域空心光束.通过轴棱锥透镜系统产生尺寸可调局域空心光束的技术，具有可控变量多、便于调节的优点.

图2 轴棱锥透镜系统产生局域空心光束Fig.2 Bottle beam generated by axicon－lens system

2 多环空心高斯光束经聚焦产生尺寸可调的局域空心光束

G.M.Philip等［22］提出聚焦多环空心高斯光束也可产生尺寸可调的局域空心光束，且产生的局域空心光束尺寸可调范围大，能量损失小，其实验装置如图3所示.

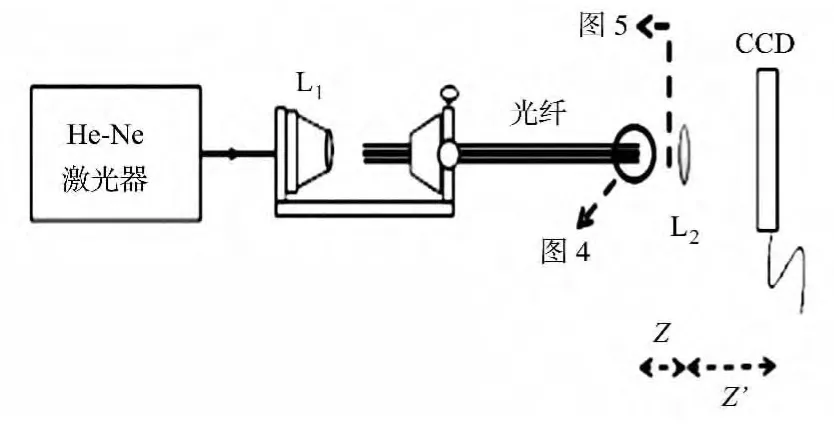
图3 聚焦多环空心高斯光束产生空心光束实验装置Fig.3 Experimental schematic diagram of generation of the tunable 3－D optical bottle beam by focusing multi－ring hollow Gaussian beam

图4 负梯度轴棱锥显微图 Fig.4 Microscope image of double－negative axicon

图5 出射光束的CCD成像图Fig.5 CCD image of the output beam

He－Ne激光器发出的非偏振激光（λ＝632.8mm）经显微物镜L1聚焦耦合到多模光纤中，在光纤的末端用化学蚀刻方法蚀刻出一个负的梯度轴棱锥（底角分别为96°，110°），如图4所示；激光在光纤中传输经过负梯度轴棱锥后，输出的LP02模［23］的中心亮斑分裂为中心为暗域的两个圆环，如图5所示.由LP02模的中心亮斑分裂而来的两个圆环之间没有相位差，这两个圆环与外侧第3个圆环之间有π个相位差［24］.输出光束的截面光强分布曲线与具有两个峰值的空心高斯光束的截面光强分布曲线相吻合，如图6所示，所以在光纤末端输出的是多环空心高斯光束［25］.

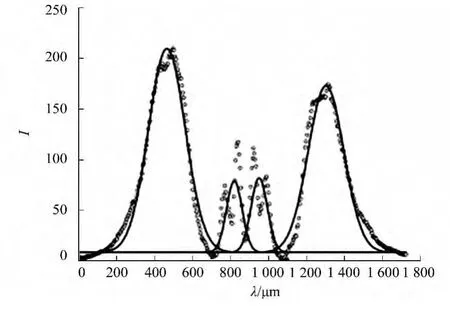
图6 输出光束与空心高斯光束光强分布比较Fig.6 Comparison of the intensity distribution between the outputbeam and the double hollow Gaussian

随后，在距离光纤端面Z处放置一消球差透镜L2，为了简化分析，认为入射到透镜L2的光束只包含两个相位差为π的环形空心高斯光束.外侧发散的环形光束经过L2聚焦后产生具有正球差的近似Bessel beam［26－27］，如图7所示.由图7可知：两束相位差为π的环形空心高斯光束经透镜聚焦后，分别产生近似Bessel beam.这两束近似Bessel beam相干叠加，即可产生周期性的局域空心光束［28－30］.此外，由实验可知在一定范围内，L2透镜与光纤端面的距离越大，局域空心光束的尺寸越大.因此，通过调节透镜L2与光纤端面的距离，可获得尺寸可调的局域空心光束.

3 新型组合正轴棱锥产生尺寸可调的局域空心光束

马亮等［31］提出一种直接产生局域空心光束的新型组合正轴棱锥，如图8所示.

由图8可以看出，它由Ⅰ，Ⅱ两个正轴棱锥胶合而成，Ⅰ底角为γ1，底面半径为a，Ⅱ底角为γ2，底面半径为b，且a＜b.新型组合光学元件由Ⅰ和Ⅱ沿各自的平面紧密胶合，沿中心轴成圆对称.因此，Ⅰ和Ⅱ底面的径向坐标相等，它的光传输特性可分为两部分：一部分为r＜a段，另一部分为a＜r＜b段.

图7 环形光束经消球差透镜聚焦后产生近似贝塞尔光束示意图Fig.7 Generation of quasi－non－diffracting beam by focusing annular ring using a lens with spherical aberration

由偏转角公式θ＝（n－1）γ可知，通过新型光学元件r＜a部分的偏转角大于a＜r＜b部分的偏转角，因此在两部分无衍射光区域之间会产生一个没有光通过的区域即局域空心光束（图8中黑实线包围的区域）.

底角为γ的传统轴棱锥产生Bessel光的最大无衍射距离Zmax≈R／［（n－1）γ］，由此可知，平行光入射到新型光学元件产生的局域空心光束的纵向长度为

图8 组合轴棱锥产生局域空心光束Fig.8 Scheme of bottle beam generated by combined axcion

因此，通过选择不同底角和底面半径的Ⅰ和Ⅱ轴棱锥，局域空心光束的纵向长度将会不同，可以方便地获得尺寸可调的局域空心光束.新型组合正轴棱锥还具有结构简单，容易加工的优点.

4 液体轴棱锥产生尺寸可调的局域空心光束

图9 液体轴棱锥产生单个局域空心光束Fig.9 Single bottle beam generated by a liquid axicon

2008年，G.Milne等［32－33］提出能产生可调谐Bessel beam的新型液体轴棱锥，但研究并未涉及bottle beam.2011年，程治明等［34］提出一种可产生尺寸可调单个局域空心光束的液体轴棱锥.此液体轴棱锥是在传统轴棱锥底部去除一个同顶角而不同底面半径的小轴棱锥，再与一个在中心挖去一小圆柱的同底面半径圆柱胶合而成.

如图9所示，若在液体轴棱锥的空腔内注入液体的折射率n2大于腔体的折射率n1，则当平面波垂直入射时，光束在半径R2＜r≤R1的区域相当于底角为γ的传统轴棱锥.光束半径0＜r≤R2的区域垂直入射到内部液体中后还要经过两次折射，即经液体折射到轴棱锥中，然后经轴棱锥折射到空气中，其光路如图10所示.

由于n1＜n2，所以有φ＜β，即0＜r≤R2的区域比R2＜r≤R1的区域对入射光线有更强的偏折能力，因此，会产生单个局域空心光束.n2越大，局域空心光束尺寸越大，反之，n2越向n1逼近，局域空心光束尺寸越小.由几何关系可知：n1＜n2时，局域空心光束尺寸随液体折射率n2减小而减小.因此，可以通过更换不同折射率的液体获得尺寸可调的局域空心光束.

液体轴棱锥通过单一元件即可获得尺寸可调的局域空心光束，具有转换效率高、光损伤阈值高，以及可多次并能方便调节的优点.

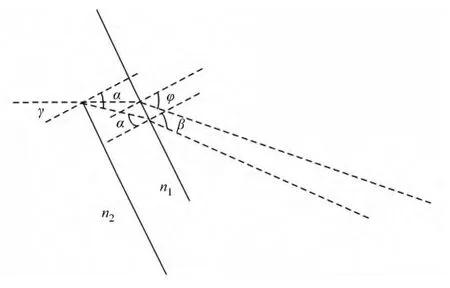
图10 光线通过液体轴棱锥光路图Fig.10 Optical path diagram of the light passes through liquid axicon

5 可拆式组合轴棱锥产生尺寸可调的局域空心光束

方翔等［35］提出一种可产生不同类型局域空心光束的可拆式组合轴棱锥.该轴棱锥是在底角为γ1的传统轴棱锥的中部轴线方向贯通开设一圆孔，在圆孔内嵌设一底角为γ2（γ2≠γ1）的第二轴棱锥，就可形成可拆式组合轴棱锥，如图11所示.

1）当γ1＜γ2时，由于经过Ⅱ部分的出射锥面波的偏转角比Ⅰ部分的偏转角大，因此Ⅰ，Ⅱ两部分产生的无衍射贝塞尔光之间会形成一段没有光通过的区域，即局域空心光束.由图11中的几何关系可以看出：局域空心光束起始位置在Zmax，1的后端点，结束位置在Zmax，2的前端点.其中Zmax，1是由半径为R2角为γ2二轴棱锥产生的贝塞尔光的最大无衍射距离；Zmax，2为半径为R2底角为γ1一轴棱锥产生的贝塞尔光的最大无衍射距离.

图11 可拆式组合轴棱锥产生局域空心光束示意图Fig.11 Scheme of bottle beam generatedby detachable combined axicon

在产生单个局域空心光束时，第一轴棱锥底角固定时，局域空心光束的最大暗域半径R及轴向长度L随着第二轴棱锥底角的增大而增大；第二轴棱锥底角固定时局域空心光束的最大暗域半径R及轴向长度随着第一轴棱锥底角增大而减小.

2）当γ1＞γ2时，入射平面波经过第二轴棱锥将形成较小偏转角的锥面波，因此Ⅰ，Ⅱ两部分产生的无衍射贝塞尔光将产生交叠，交叠的两束光具有相同频率，不同的径向波矢分量，交叠的两束贝塞尔光干涉将产生周期性的局域空心光束.周期性的局域空心光束的周期为

在产生周期性局域空心光束时，改变第二轴棱锥底角（或第一轴棱锥底角）将会改变轴向波矢分量，即也会改变周期性局域空心光束区域的位置，相干区域的轴向长度和局域空心光束自再现周期.所以通过更换不同底角的第二轴棱锥（或第一轴棱锥），可形成不同尺寸的单个局域空心光束或不同参量的周期性局域空心光束.可拆式组合轴棱锥元件加工相对容易、结构简单、容易操控.

6 结论

通过对上述5种方法的分析可以发现，产生尺寸可调的局域空心光束的技术大致可分为三类：一类是通过传统的轴棱锥透镜系统产生尺寸可调的局域空心光束；一类是通过新型轴棱锥如新型组合正轴棱锥，液体轴棱锥，可拆式组合轴棱锥产生尺寸可调的局域空心光束；还有一类是通过光纤透镜系统聚焦多环空心高斯光束来产生尺寸可调的局域空心光束.后两类技术的原理都是将产生的两束不同径向波矢的贝塞尔光相干叠加来获得局域空心光束，并通过调节某一变量来调节局域空心光束的尺寸.

在这三类技术中，通过轴棱锥透镜系统的技术可控变量多，便于调节.通过新型轴棱锥来产生尺寸可调局域空心光束的技术易于操作、抗干扰能力强、便于设备集成化.通过光纤透镜系统聚焦多环空心高斯光束的技术操作简单、局域空心光束尺寸可调范围大、能量损失小.产生尺寸可调的bottle beam的技术还在不断发展［36－38］.

局域空心光束已经成为捕获和操控微观粒子的重要工具［39］，并且在生物细胞操控等领域有着重要的应用，不同尺寸的局域空心光束可囚禁或操控不同尺寸的粒子或细胞，对于其他应用也有重要影响，根据应用环境的不同，选用不同的产生尺寸可调局域空心光束的技术具有极高的实用价值.如何产生既便于调节，又便于设备集成化、尺寸可调范围大的局域空心光束的技术值得更深入的研究.

［1］DURIN J.Exact solutions for nondiffracting beams［J］.J Opt Soc Am A，1987，4（4）：651－654.

［2］ASHKIN A.Acceleration and trapping of particles by radiation pressure［J］.Phys Rev Lett，1970，24（4）：156－159.

［3］ARLT J，PADGETT M J.Generation of a beam with a dark focus surrounded by regions of higher intensity：The optical bottle beam［J］.Opt Lett，2000，25（4）：191－193.

［4］TATARKOVA S A，SIBBETT W，DHOLAKIA K.Brownian particle in an optical potential of the washboard type［J］.Phys Rev Lett，2003，91（3）：1－4.

［5］GARCES－CHAVEZ V，MCGlOIN D，MELVILLE H，et al.Simultaneous micromanipulation in multiple planes using a self－reconstructing light beam［J］.Nature，2000，419（4903）：145－147.

［6］PATERSON L，MACDONALD M P，ARLT J，et al.Controlled rotation of optically trapped microscopic particle［J］.Science，2001，292（5518）：912－914.

［7］MACDONALD M P，PATERSON L，VOLKE－SEPULVEDA K，et al.Creation and manipulation of three dimentional optically trapped structures［J］.Science，2002，296（5570）：1101－1103.

［8］GRIER D G.A revolution in optical manipulation［J］.Nature，2003，424（6950）：810－816.

［9］马亮，吴逢铁，马宝田.阶变折射率轴棱锥产生光学bottle beams［J］.物理学报，2010，59（9）：6096－6100.

［10］张前安，吴逢铁，郑维涛，等.新型锥透镜产生局域空心光束［J］.物理学报，2011，60（9）：094201.

［11］程治明，吴逢铁，方翔，等.圆顶轴棱锥产生多个bottle beam［J］.物理学报，2012，61（21）：214201.

［12］CHÁVEZ－CERDA S，NEW G H C.Evolution of focused Hankel waves and Bessel beams［J］.Optics Communications，2000，181（4／5／6）：369－377.

［13］WEI M D，SHIAO W L，LIN Y T.Adjustable generation of bottle and hollow beams using an axicon［J］.Optics Communications，2005，248（1／2／3）：7－14.

［14］PU Ji－xiong，DONG Mei－mei，WANG Tao.Generation of adjustable partially coherent bottle beams by use of an axicon－lens system［J］.Applied Optics，2006，45（29）：7553－7556.

［15］刘彬，吴逢铁，刘岚.透镜焦距对局域空心光束尺寸的影响［J］.中国激光，2008，35（3）：406－409.

［16］AHLUWALIA B P S，YUAN X C，TAO S H.Generation of self－imaged optical bottle beams［J］.Opt Commun，2004，238（1／2／3）：177－184.

［17］吴逢铁，卢文和，马宝田.轴棱锥：镜系统的光束传输与变换［J］.光学学报，2009，29（9）：2557－2560.

［18］YELIN D，BOUMA B E，TEARNEY G J.Generating an adjustable three－dimensional dark focus［J］.Opt Lett，2004，29（7）：661－663.

［19］曾夏辉，吴逢铁，刘岚.干涉理论对bottle beam的描述［J］.物理学报，2007，56（2）：791－797.

［20］MCGlOIN D，SPALDING G C，MELVILLE H，et al.Three－dimentional arrays of optical bottle beams［J］.Opt Commun，2003，225（4／5／6）：215－222.

［21］刘岚，吴逢铁.衍射理论对局域空心光束及无衍射光束重建的描述［J］.光学学报，2008，28（2）：370－374.

［22］PHILIP G M，VISWANATHAN N K.Generation of tunable chain of three－dimensional optical bottle beams via focused multi－ring hollow Gaussian beam［J］.J Opt Soc Am A，2010，27（11）：2394－2401.

［23］SNYDER A W，LOVE J D.Optical waveguide theory［M］.New York：Chapman and Hall Ltd，1983：23－24.

［24］VISWANATHAN N K，PHILIP G M，JAYASURYA Y V.Generic dark hollow beams using negative cones chemically etched in fiber tips［J］.Proc SPIE，2010，7613：［doi：10.1117／12.841471］.

［25］CAI Yang－jian，LU Xuan－hui，LIN Qiang.Hollow Gaussian beams and their propagation properties［J］.Opt Lett，2003，28（13）：1084－1086.

［26］HERMAN R M，WIGGINS T A.Production and uses of diffractionless beams［J］.J Opt Soc Am A，1991，8（6）：932－942.

［27］BURVALL A，KOLACZ K，JAROSZEWICZ Z，et al.Simple lens axicon［J］.Appl Opt，2004，43（25）：4838－4844.

［28］吴逢铁，曾夏辉.相干贝塞尔光产生具有塔尔博特效应的局域空心光束［J］.光学学报，2008，28（1）：174－178.

［29］CHAVEZ－CERDA S，TEPICHIN E，MENESES－NAVA M A，et al.Experimental observation of interfering Bessel beams［J］.Opt Express，1998，3（13）：524－529.

［30］CHAVEZ－CERDA S，MENESES－NAVA M A，HICKMANN J M.Interference of traveling nondiffracting beams［J］.Opt Express，2003，11（2）：158－166.

［31］马亮，吴逢铁.新型组合正轴棱锥产生局域空心光束［J］.红外与激光工程，2011，40（10）：1988－1991.

［32］MILNE G，JEFFRIES G D M，CHIUA D T.Tunable generation of Bessel beams with a fluidic axicon［J］.Applied Physics Letters，2008，92（26）：261101.

［33］AKTURK S，ARNOLD C L，PRADE B，et al.Generation of high quality tunable Bessel beams using a liquid immersion axicon［J］.Optics Communications，2009，282（16）：3206－3209.

［34］程治明，吴逢铁，张前安，等.液体轴棱锥产生尺寸可调的单个局域空心光束［J］.光学学报，2011，31（10）：1008001.

［35］方翔，吴逢铁，程治明.产生不同类型局域空心光束的可拆式组合轴棱锥［J］.光学学报，2012，32（8）：0826002.

［36］GENEVET P，DELLINGER J，BLANCHARD R，et al.Generation of two－dimensional plasmonic bottle beams［J］.Opt Express，2013，21（8）：10295－10300.

［37］CHEN Yu－hao，YAN Lu，STEINVURZEL P，et al.Bottle beam generation from fiber－based Bessel beams［C］∥Conference on Lasers and Electro－Optics.San Jose：［s.n.］，2012：1－2.

［38］CHEN Yu－hao，YAN Lu，RISHØJ L，et al.Dynamically tunable optical bottles from an optical fiber［J］.Opt Lett，2012，37（16）：3327－3329.

［39］XU Peng，HE Xiao－dong，WANG Jin，et al.Trapping a single atom in a blue detuned optical bottle beam trap［J］.Opt Lett，2010，35（13）：2164－2166.